连续屈服材料屈服强度测量不确定度的评定

梁明华,赵志伟,李永明,谢小东

(1.中国石油集团工程材料研究院有限公司,国家市场监管重点实验室(石油管及装备质量安全) 陕西 西安 710077; 2.巨龙钢管有限公司 河北 沧州 062658; 3.中国石油长庆油田公司 陕西 西安 712000)

0 引 言

拉伸试验所得到的屈服强度是金属材料最重要的力学性能指标之一,其对产品设计、选材、使用、产品质量控制和设备安全评估等都具有重要的应用价值[1]。在屈服强度的测试过程中,测量不确定性始终存在于测量结果中[2]。近年来,各领域对实验室检测结果的准确度和可靠性要求越来越规范,特别是在出具有法律效力的第三方报告时,除了要包含准确的检测结果以外,在报告中还应有检测结果的测量不确定度[3-4]。因此,金属材料屈服强度的检测结果应进行测量不确定度的评定。

金属材料的屈服过程可分为连续屈服和不连续屈服[5]。对于不连续屈服材料,力-延伸曲线中存在一段水平的台阶,此阶段的特点是应力不增加(甚至降低)而应变继续增加。不连续屈服金属材料的屈服强度有上屈服强度(Upper yield strength,ReH)或者下屈服强度(Lower yield strength,ReL),这2种屈服强度可不加持引伸计通过力-位移曲线直接读取,即不连续屈服材料的屈服强度检测结果不确定度与引伸计不相关。而对于连续屈服材料,力-延伸曲线中不存在水平的台阶,力随延伸增加而增加。连续屈服材料的屈服强度一般有规定塑性延伸强度(Proof strength, plastic extension,Rp)或规定总延伸强度(Proof strength, total extension,Rt),这2种屈服强度必须夹持引伸计,通过力-延伸曲线求取,即连续屈服材料的屈服强度检测结果不确定度来源需考虑引伸计。在GB/T 228.1—2021《金属材料 拉伸试验 第一部分:室温试验方法》附录O中有如下叙述:如果屈服强度的测量是通过力-延伸曲线求取,且测量力随延伸的变化而有较大的变化,则由引伸计所确定并报告的力值不确定度可能在各力值不确定度分量中占主要因素。金属材料的连续屈服模式正属于这种情况,但标准中未给出该类不确定度的评定方法。在众多文献中[2-4,6-10],仅给出了不连续屈服材料的屈服强度(ReH或ReL)不确定度评定方法或未将引伸计所确定并报告的力值不确定度进行综合分析。

本文采用国内某厂生产的X80M管线钢棒状拉伸试样开展屈服强度(Rp0.2)的不确定度评定,采用标称直径10 mm的棒状拉伸试样,检测方法为GB/T 228.1—2021,使用UTM5305电子拉伸试验机(0.5级)和Epsilon引伸计(0.5级)进行试验,对连续屈服材料屈服强度不确定度进行评定。

1 2种屈服模式典型曲线的对比

图1和图2分别是实验室两种金属材料不连续屈服和连续屈服模式的载荷-变形拉伸曲线,其中图1材料为常用的20#钢,图2材料为X80管线钢。从图1可以看出,初始段为材料的弹性变形阶段,在这一阶段试样受的载荷大小与试样的变形成比例关系。在此阶段材料在拉伸力作用下改变其尺寸和形状,当卸除拉伸力后,可恢复为原来尺寸和形状。弹性变形阶段超过上屈服点后进入屈服阶段,此阶段存在拉伸力不增加或甚至下降的情况下,而变形继续增加的现象,即物理屈服现象。材料的上屈服强度(ReH)和下屈服强度(ReL)均在这一阶段获得。屈服阶段后材料进入均匀塑性变形阶段,必须进一步增加拉伸力使试样继续被拉长。超过最大载荷后,材料进入局部塑性变形阶段,强化能力小于塑性变形的速度,变形集中在局部地区进行,形成缩颈现象。随着拉伸继续进行,缩颈部位的材料继续被拉长,直至被拉断。在该曲线的屈服阶段,屈服强度(ReH或ReL)可不安装引伸计通过力-位移曲线直接读取,因此屈服强度的测量不确定度和引伸计不相关。

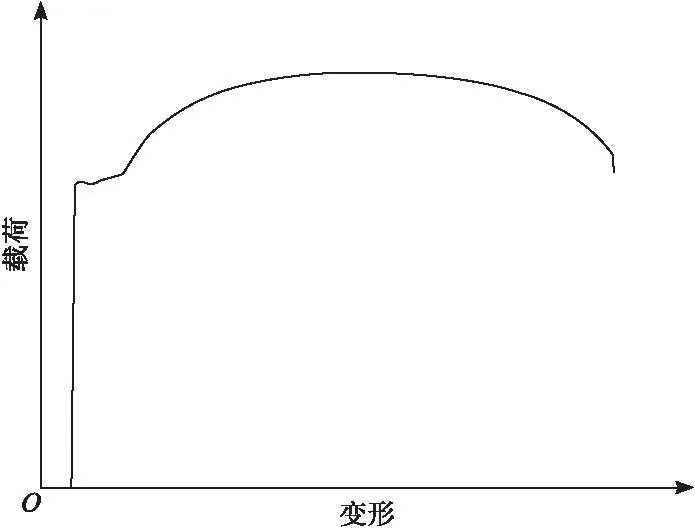
图1 20#钢不连续屈服模式载荷-变形曲线

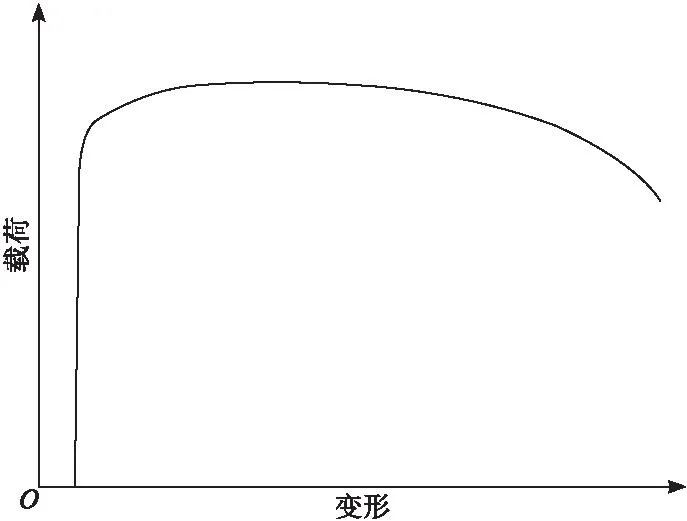
图2 X80管线钢连续屈服模式载荷-变形曲线

从图2可以看出,X80管线钢载荷-变形拉伸曲线弹性变形阶段与图1相同,弹性变形阶段进入屈服阶段后,曲线没有明显的屈服平台,呈圆屋顶(Round house)型,屈服阶段和均匀塑性变形阶段没有明显的分界点。在该曲线的屈服阶段,拉伸曲线不存在水平的台阶,应力随应变增加而增加。此种情况下必须通过引伸计获取连续屈服材料的屈服强度,因此屈服强度检测结果不确定度来源需考虑引伸计。下面重点分析金属材料的连续屈服模式即图2曲线模式下的屈服强度(Rp0.2)不确定度评定方法。

2 连续屈服材料X80M管线钢屈服强度Rp0.2模型

根据GB/T 228.1—2021,Rp0.2通过以下计算式得到:

(1)

本试验的测量结果为:

d0=9.986 mms0=78.320 mm2Fp0.2=48.87 kN

计算结果为:

(2)

3 屈服强度Rp0.2测量不确定度主要来源分析

根据试样在检验过程中的试验特点,经分析可知屈服强度Rp0.2测量不确定度主要来源于以下几个方面[10]:1)棒状拉伸试样直径(d)的测量所引入的不确定度分量u(d),包含所用千分尺误差所引入的不确定度和试验人员测量过程所带来的影响。2)试验设备及装置力值测量所引入的不确定度分量u(Fp0.2),包含试验设备示值所引入的不确定度分量u1(Fp0.2)、标准测力仪所引入的标准不确定度u2(Fp0.2)和延伸测量用引伸计所引入的不确定度分量u3(Fp0.2)。3)检验结果修约而引入的不确定度分量u(Rp0.2,rou)。

4 屈服强度Rp0.2标准不确定度分量的评定

4.1 由试样直径测量而引入的不确定度分量评定

4.1.1 试样工作段直径测量引入的不确定度分量u1(d)的评定

棒状试样的公称直径d为10 mm,在相同的条件下5位实验人员分别对试验用单根试样进行了10次测量,测量结果见表1。

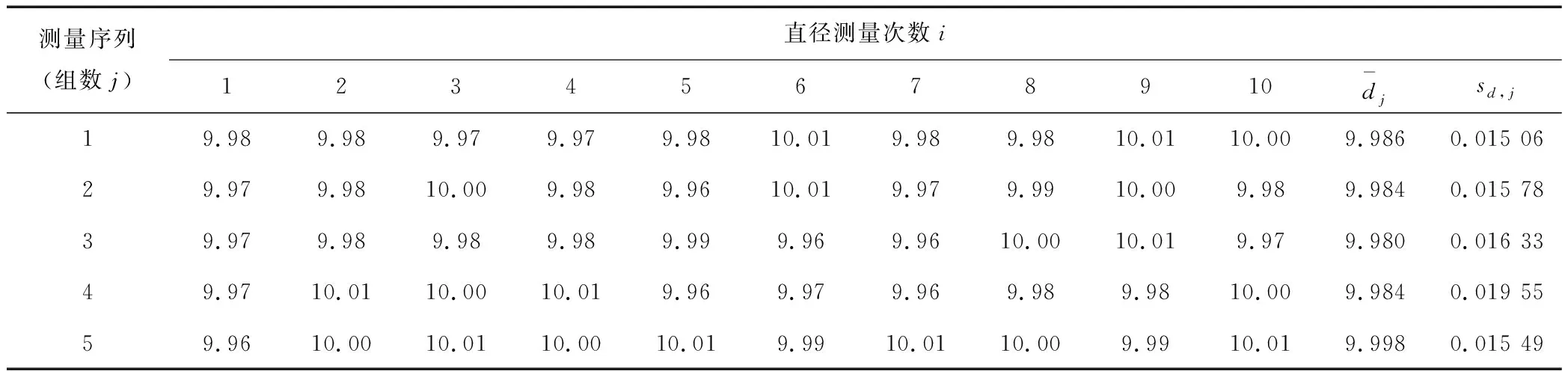
表1 试样工作段直径d测量数据表 mm

直径的合并样本标准差为:

(3)

标准差sd,j数列的标准差为:

(4)

因为

4.1.2 由测量试样尺寸所用量具引入的不确定度分量u2(d)的评定

本试验中棒状试样直径d的测量采用量程为0～25 mm的1级千分尺。其极限误差为±0.004 mm,即误差范围为[-0.004 mm,+0.004 mm],在测量过程中误差出现概率服从矩形分布。因此由千分尺引入的标准不确定度可用B类评定方法进行评定,其中A为测量误差的区间半宽。

4.1.3 试样直径结果的不确定度分量u(d)

因为u1(d)和u2(d)相互独立,所以棒状试样最终直径的测量标准不确定度可以通过下式计算:

4.2 由试验力测量误差而引入的不确定度分量u(Fp0.2)的评定

4.2.1 由试验机示值误差引入的不确定度分量u1(Fp0.2)的评定

本试验中,使用UTM5305电子拉伸试验机,试验机经检定为0.5级,示值误差±0.5%,示值误差在测量过程中出现在该区间的概率服从均匀分布,可用B类不确定度评定。

4.2.2 计量用测力仪引入的标准不确定度u2(Fp0.2)

试验机是通过计量机构使用0.1级标准测力仪进行检定,标准测力仪的不确定度为0.1%,k为2,因此标准测力仪引入的B类相对标准不确定度为:

4.2.3 试验用引伸计的误差所引入的测量不确定度u3(Fp0.2)

引伸计标距误差与系统相对误差引起的Fp0.2测量误差与F-ΔL曲线在Fp0.2附近误差区间的斜率有关。根据试验所得的F-ΔL曲线,在获取Fp0.2时,曲线的切线斜率越大,引伸计误差对Fp0.2的不确定度影响越大。当曲线的切线与横轴的夹角为45°时,其斜率为1。当夹角小于45°时,斜率变小。当曲线处于平台时,切线平行于横轴,斜率为零,此时引伸计误差对Fp0.2无影响。系统相对误差和标距误差在Fp0.2附近的误差区间的概率服从均匀分布,k=3。此两项误差引起的标准不确定度相同,且彼此不相关,可用B类不确定度评定,用下式表示:

(5)

式(5)中,第一项为引伸计系统相对误差引入的不确定度,第二项为引伸计标距误差引入的不确定度。其中,A为引伸计系统相对误差或引伸计标距误差区间的半宽度。因所用引伸计为0.5级引伸计,因此A值为0.5%;G为F-ΔL曲线在Fp0.2附近引伸计误差区间的斜率,可以用下式计算:

(6)

于是上式化为绝对不确定度后为:

本试验中,拉伸曲线及Fp0.2区域附近的局部放大图如图3所示,所取的屈服点引伸计伸长量为0.252 mm,拉力值为48.87 kN。通过计算,Fp0.2处的斜率为0.46,因此可进行如下计算:

图3 X80管线钢载荷-引伸计变形曲线

4.2.4Fp0.2测量误差所引入的不确定度分量

上述三项不确定度分量之间为独立的关系。因此,屈服力Fp0.2力值测量所引入的不确定度分量为:

4.3 Rp0.2数值修约引入的标准不确定度分量u(Rp0.2,rou)

实验室工作中,最终检验结果应按照标准要求进行修约,因此这必定引入了不确定度。按照我国GB/T 228.1—2021标准第22条规定,本试验中强度性能修约到1 MPa。对于金属材料拉伸性能试验结果的数值修约所带来的不确定度,按照B类不确定度的评定公式,修约间隔为δx,则u(x)=0.29δx。

本试验中,Rp0.2的修约间隔为1 N/mm2,可得:

u(Rp0.2,rou)=0.29×1=0.29 N/mm2

5 合成标准不确定度的计算

用于评定并计算Rp0.2测量结果合成标准不确定度所需要的各标准不确定度分量汇总表见表2。

表2 标准不确定度分量汇总表

因试样计算直径d的测量、试验力Fp0.2以及数值修约所引入的不确定度之间彼此独立不相关。因此,由下式计算合成标准不确定度:

(7)

所以,

(8)

即

(9)

由测量数学模型式1,对如上所述各输入量(Fp0.2、d)求偏导数,可得相应的不确定度灵敏系数:

代入式(9),可得:

=4.72+1.50+0.08=6.30 N2mm-4

可得本试验中,RP0.2的合成标准不确定度为:

uc(Rp0.2)=2.51 N/mm2

通过标准不确定度的评定可发现,在该试验条件下影响屈服强度(Rp0.2)不确定度的主要因素为试验机示值误差和引伸计误差所引入的不确定度。若进一步降低屈服强度(Rp0.2)测量结果不确定度,应该在试验机力值误差和引伸计误差方面进行严格控制,且在使用范围内,应尽量减少在屈服点附近(引伸计的伸长量约为0.25 mm)引伸计误差和试验机力值的误差。

6 扩展不确定度的评定及报告

扩展不确定度是由合成标准不确定度乘包含因子k来得到。k值一般取2～3,当k=2时,置信概率约为95%;当k=3时,置信概率约为99%。本试验中取包含因子k=2,区间的置信概率约为95%。

U(Rp0.2)=2×uc(Rp0.2)=2×2.51≈5 N/mm2

不确定度的相对形式为:

Urel(Rp0.2)=U(Rp0.2)/Rp0.2=5/624=0.8%

因此本试验中,不确定度报告如下:

Rp0.2=624 N/mm2,U=5 N/mm2,k=2

如果扩展不确定度以相对形式报告,则:

Rp0.2=624 N/mm2,Urel(Rp0.2)=0.8%,k=2

上述不确定度结果表明,塑性延伸强度Rp0.2的测量结果在(624±5)或(624±0.8%) N/mm2区间内的概率为95%。

7 结 论

1)应用本设备和本试验方法而得到的X80M钢的屈服强度(Rp0.2)测量结果扩展不确定度为:Rp0.2=624 N/mm2,U=5 N/mm2,k=2。

2)在该试验条件下影响屈服强度(Rp0.2)扩展不确定度的主要因素为试验机示值误差和引伸计误差所引入的不确定度。

3)为进一步降低屈服强度(Rp0.2)测量结果不确定度,应该严格控制试验机的力值误差和引伸计的误差,且尽量减少在屈服点附近(引伸计的伸长量在0.25 mm左右)引伸计误差和试验机力值的误差。