基于图像的三维裂隙岩体特征提取、简化及网格生成方法
刘骏标,邢会林,姜素华,闫伟超
(1.深海圈层与地球系统教育部前沿科学中心,海底科学与探测技术教育部重点实验室,中国海洋大学 海洋地球科学学院,山东 青岛 266100;2.崂山实验室,山东 青岛 266237;3.中国海洋大学 海底科学与工程计算国际中心,山东 青岛 266100;4.崂山实验室 海洋矿产资源评价与探测技术功能实验室,山东 青岛 266237)
近年来,数字岩石物理(Digital Rock Physics,DRP)技术被广泛应用于二维或三维岩石图像处理中[1-3],以取代复杂的岩石物理实验(如渗透率、弹性模量及电导率等岩石物理参数)。得益于CT等成像技术的发展,可以得到岩石的不同分辨率的二维或三维图像(从纳米到厘米尺度)[4-5]。裂隙作为岩石非均质性的重要组成部分,可在高分辨率CT图像中被识别出来[6]。若按照目前常用的方法,在进行图像可视化及后续数值模拟时,为了精确表示出细小的裂隙,需要将所有体素点全部转为规则正方体网格。然而,这种方法不仅将产生一个巨大的网格数据集,还将额外增加模拟计算量。因此,需要提出一种在保留裂隙主要几何特征的同时实现数据简化及生成计算分析所必需的网格的方法。
基于有限元或有限体积法的数值模拟分析依赖于可用的合适网格[7]。K.Terada等[8]将所有体素点直接转换为正方体网格,此方法简单直接,但将产生更大的数据集和锯齿边界,且锯齿边界处的模拟精度难以得到保证并最终影响模拟结果[9];W.E.Lorensen等[10]、Wu Z.J.等[11]、Zhang Y.J.等[12-13]、D.Boltcheva等[14]分别就移动立方体法及其拓展、基于八叉树的四面体或六面体网格生成方法、德劳内细化算法进行了深入研究,并应用于网格生成领域,此类方法通过识别出外轮廓或材料之间的边界曲面,生成相应的体积模型,但是在生成裂隙与围岩之间的边界曲面时,由于裂隙厚度较小,需要生成大量小尺寸的网格才能保证材料边界曲面的质量,且其生成的三维网格模型并不适用于仿真分析;A.Paluszny等[15]和Liu Y.等[16-17]通过一系列三维线或面表示裂隙,此类方法能用有限数量的高质量三角形网格来描述裂隙的主要几何特征,显著减少了网格数目,并能以三维裂隙面为约束生成非结构化四面体网格,因此本文在后续将使用该方法。
本文提出了一种有效的特征提取、简化及网格生成方法,主要工作为:①利用中心面点提取算法对裂隙的特征进行提取,将裂隙数据体简化为一系列面;②利用简化质心Voronoi法来对一系列面生成简化质心Voronoi图,并基于质心点进行裂隙面网格生成、面片交叉标识、网格修复及优化;③采用对生成的裂隙面网格进行图像数据体还原的方式,对所生成的网格的代表性及其精度进行体素相似度和形状相似度评估;④以所生成的裂隙面网格和相应的岩石边界为约束,生成四面体网格模型,并用最小二面角、半径比、边长比及体积比等参数对四面体网格质量进行评价。
1 裂隙特征提取简化网格生成及评价方法
裂隙特征提取是指从岩石数字图像中提取裂隙的形态、大小、分布等几何特征的过程,旨在对岩石的微观结构进行精确分析和建模。本文首先会对原始数字岩石图像数据进行二值化、拓展[17]、膨胀与腐蚀等预处理操作。其中,二值化操作后数据将被分为基质和裂隙,拓展操作则能将裂隙面上的小孔洞补全,而先腐蚀后膨胀操作可以消除3D图像上的细小噪声并平滑裂隙边界。在预处理之后,本文将使用以下方法对三维岩石图像裂隙进行特征提取、简化、网格生成、还原及评估,然后以生成的面为约束生成四面体网格。
1.1 裂隙特征提取、简化及其网格生成
为将裂隙提取为一系列三维面从而得到裂隙的几何特征,本文采用中心面点提取算法提取出裂隙的中心面点[16]。某个裂隙体素点v的26邻域如图1所示,分为8个区域(每个小立方体为一独立区域),如果这8个区域都符合公式(1),则认为这个裂隙体素点v为中心面点。
(1)
式中:N(v)为裂隙体素点v的26邻域,Ni(v)为N(v)第i个分区,|·|代表每个分区中裂隙体素点的数目。例如,对一个81×81×3的裂隙数据进行中心面点提取算法后,得到79×79×1的裂隙中心面点数据。

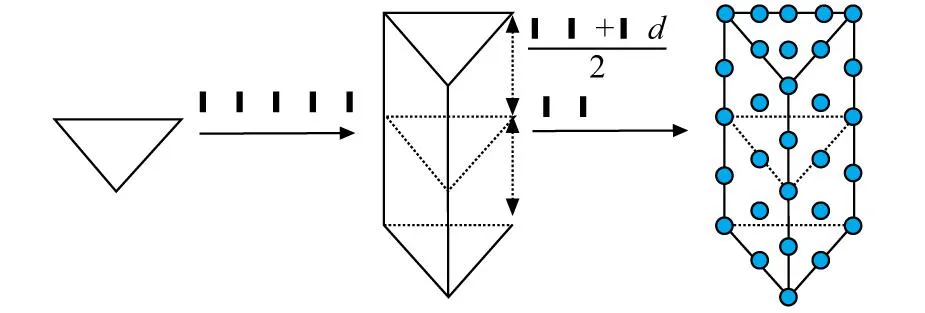
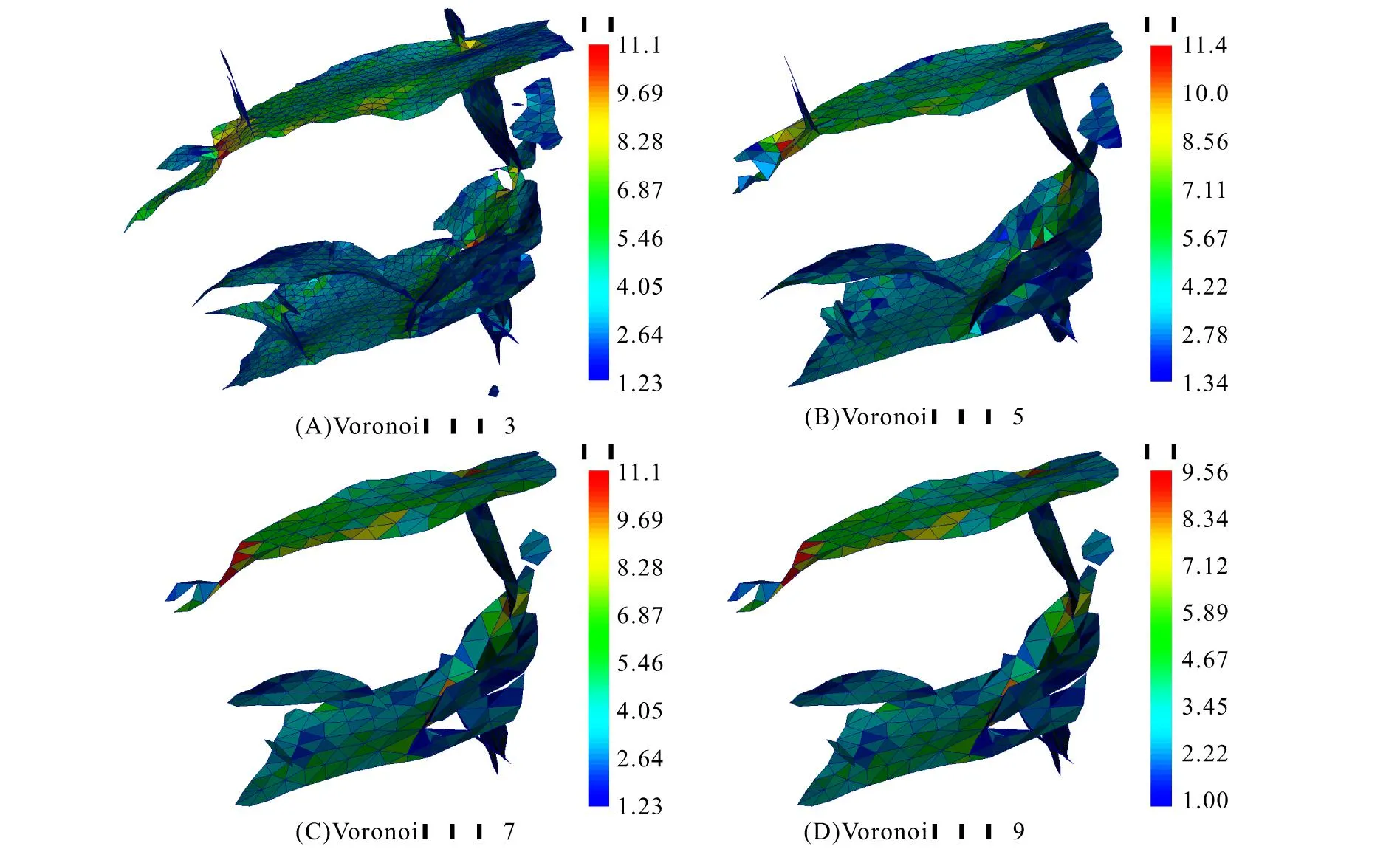
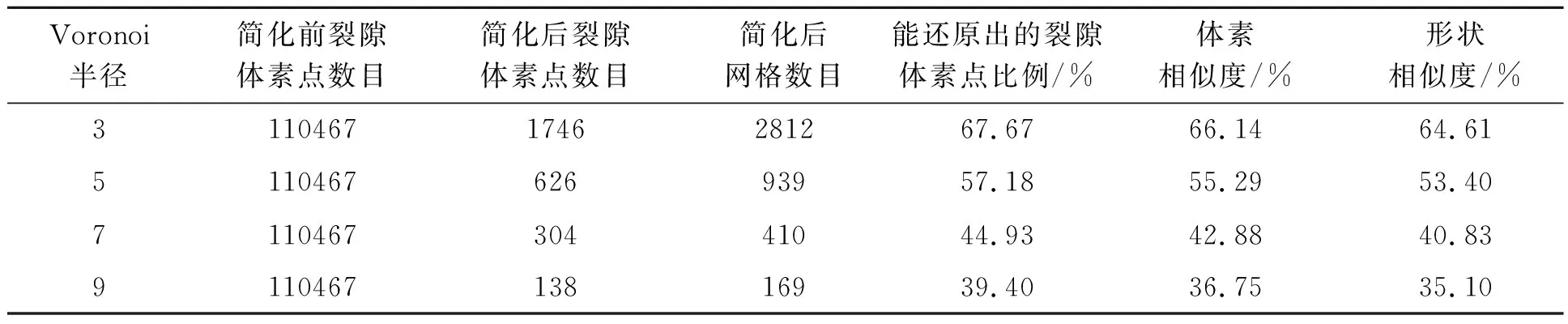
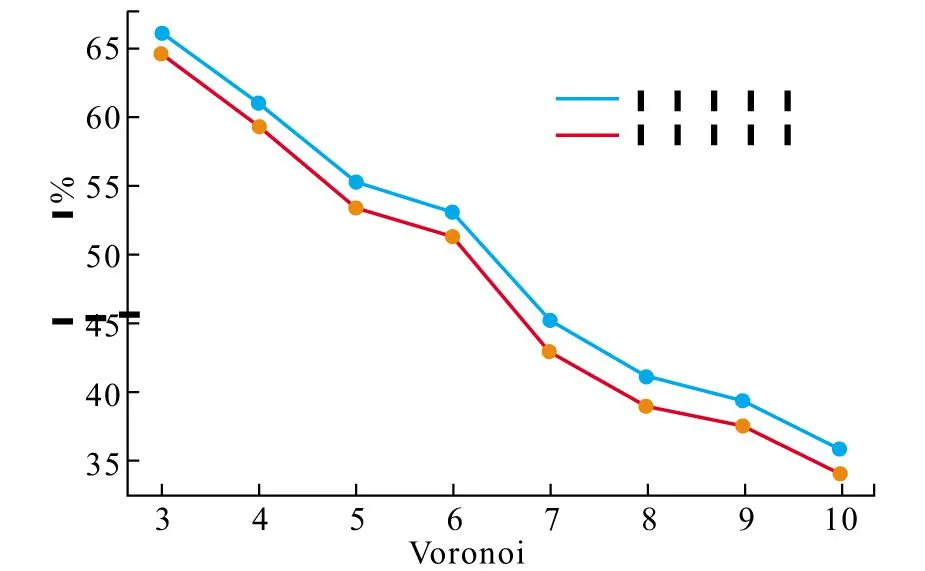
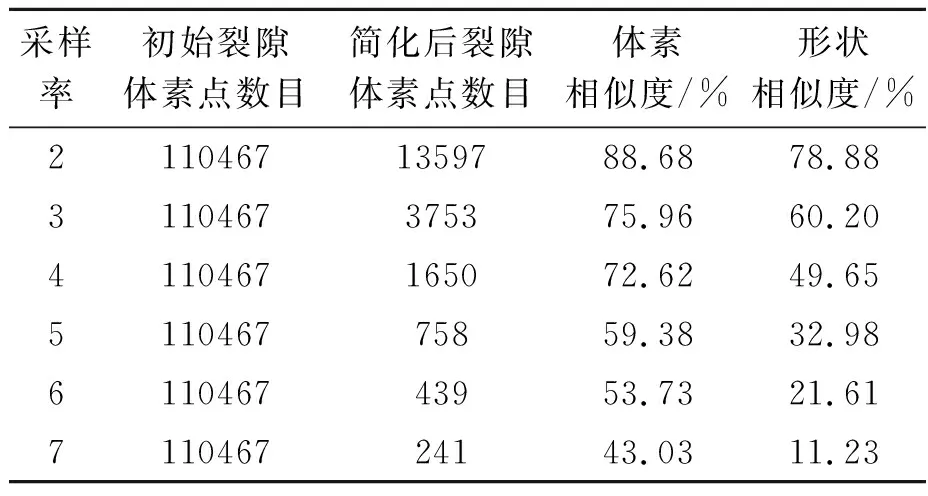
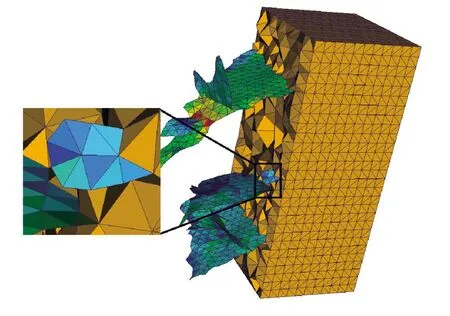
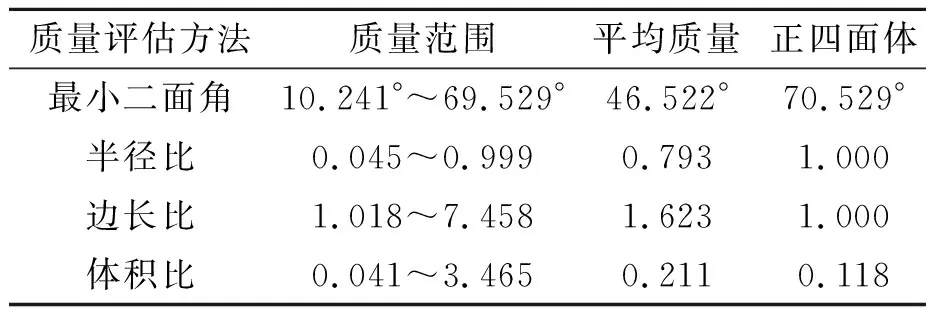
Vi={x∈Ω|dis(x,zi) (2) 式中:dis(·)为RN中的欧几里得范数,生成器zi也可被称为Voronoi单元的质心: (3) 式中:ρ(x)是Vi的密度函数。 简化质心Voronoi图法对Voronoi图法做了2点限制:①假设各组裂隙被提取为一系列的平面,厚度变为1,裂隙由一组具有相同体积和密度的体素表示,因此公式(3)中的ρ(x)=1;②由于裂隙被提取为一系列的平面,在构建Voronoi图时,采用广度优先搜索方法(Breadth First Search Method)传播Voronoi单元[19]。 (4) 式中:Cvol为裂隙的总体素点数目,t为裂隙的平均厚度。r为自定义的Voronoi半径,决定着Voronoi单元的传播距离。因为Cvol和t是已知的,所以Voronoi半径r为简化质心Voronoi图法的唯一变量。 利用简化质心Voronoi图法生成n个质心点后,本文将基于这些质心点生成三角形网格,并进行面片交叉标识、网格修复及优化[16],用上述方法对79×79×1的裂隙中心面点数据处理后结果如图2所示。 图2 三角形网格生成流程Fig.2 Generation process of triangular mesh 本文采用对生成的网格进行图像数据体还原的方式,对所生成的网格的代表性及其精度进行相似度评估。在进行图像数据体还原前,需要在生成的裂隙网格上添加厚度属性,厚度的计算方法如下: a.对所有裂隙点进行判断:当一个点的上下左右前后有一个体素点为基质时,这个点为外边界点; b.算出每个三角形网格的重心与所有外围点的最小距离r; c.将最小距离r乘以2作为厚度。 在赋予三角形网格厚度属性后,本文会把带厚度属性的三角形网格还原回三维图像数据,数据还原方法如下: a.当三角形网格不平行于XY、XZ、YZ平面时,利用三角形网格的重心与所有外围点的最小距离求厚度值方法一般会导致厚度值偏小,所以本文对所有三角形网格都加上一个额外厚度Δd。在本文中,额外厚度Δd设置为1; b.根据每个三角形网格的厚度将每个三角形推成三棱柱; c.标记此三棱柱内部的所有体素点,这些被标记的体素点就是简化后网格所能还原出来的体素点。 数据还原过程如图3所示。 图3 数据还原过程Fig.3 Data restoration process 数据还原后,将进行以下2种相似度判断[17]: a.体素相似度: (5) b.形状相似度: (6) 式中:Cmesh代表的是还原后裂隙点的数目,Cimage代表的是原始数据裂隙点的数目。Cmesh,in代表的是还原后的裂隙与输入图像裂隙相同点的数目,Cmesh,out表示还原后裂隙与输入图像裂隙中不同点的数目,即Cmesh,out=Cmesh-Cmesh,in,Svoxel的取值范围为[0,1],Sshape的取值范围为[-∞,1]。 为证明本文方法能有效地应用于具有复杂裂隙的三维岩石图像,本文选取了一个128×128×60的二值化岩石裂隙图像数据,图像数据如图4所示。 图4 数字岩石图像与裂隙Fig.4 Digital rock image and fractures 从图4-A中可看出此图像数据已被分为基质(蓝色)和裂隙部分(红色),图4-B为该数据的裂隙部分。用本文方法对数据的裂隙部分进行特征提取、简化及网格生成,以不同Voronoi半径为参数生成的网格如图5所示。 从图5可看出,随着Voronoi半径的增大,裂隙面网格越来越大,图像也越加简化并丢失更多信息,尤其是宽度小或长度小的裂隙更容易被简化掉。Voronoi半径与相似度的关系如图6所示,网格数据如表1所示。 从图6可以看出,随着Voronoi半径的增大,体素相似度与形状相似度都降低,且体素相似度与形状相似度的差基本不变。原始数据中裂隙点数目为110 467,占总体素点数目11.24%,表1中的简化后网格数目表明本文方法能用少量的网格代表大量的裂隙点。此外,当形状相似度高于60%时,本文方法生成的网格就能较好地代表原始裂隙。例如,当Voronoi半径选为3时,形状相似度为64.61%。从图4-B与图5-A中可以看出,生成的网格基本保留了裂隙的主要几何特征。 图5 基于不同Voronoi半径生成的裂隙面网格Fig.5 Generated fracture surface meshes based on different Voronoi radius 表1 网格数据Table 1 Mesh data 图6 Voronoi半径与相似度的关系Fig.6 The relationship between Voronoi radius and similarity 考虑到原始数据是三维图像数据,对体素点进行均匀采样可以降低图像分辨率、简化数据和减少数据集的规模,但这种方法存在相似度急剧下降和体素相似度与形状相似度之差增大的问题,如表2所示。表1中显示,采用本文方法计算的体素相似度与形状相似度之差最大仅为2.05%。与之相比,表2中均匀采样法的体素相似度与形状相似度之差最小就高达9.8%。因此,相比于均匀采样,本文方法能保持体素相似度与形状相似度的差基本不变,说明本文所提简化方案可以较好地代表原始裂隙。 本文以裂隙面网格(图5-A)和相应的岩石边界为约束,生成四面体网格模型(图7)。从图7中黑框区域可看出,四面体网格模型是基于裂隙面网格的节点约束而生成的。 通过采用最小二面角、半径比、边长比和体积比等4种网格质量度量参数[20],可以评价图7中四面体网格模型的网格质量,计算结果如表3所示。从表3中的质量数据范围及其平均数据可以看出,生成的四面体网格平均质量接近于理想的正四面体网格,网格质量较好。 表2 不同采样率时的图像数据Table 2 Image data at different sampling rates 图7 共有9 137节点和46 486个四面体网格的四面体网格模型Fig.7 A tetrahedral mesh model with a total of 9 137 nodes and 46 486 tetrahedral meshes 表3 网格质量Table 3 Mesh quality 本文以一个128×128×60的二值化岩石裂隙图像数据为例子,将裂隙提取为一系列平面并进行网格生成与相似度评估,然后以所生成的裂隙面网格与相应的岩石边界为约束,利用自行研制的四面体网格生成程序生成了质量较好的四面体网格模型。得到如下主要结论: a.提出了一种既能保留裂隙主要特征又能显著降低数据量的网格生成方法,通过中心面点提取算法、网格生成和厚度计算,达到用有限数量的高质量三角形网格来描述裂隙的主要几何特征的目的,并探讨了不同Voronoi半径参数与方法效果的关系。 b.在示例中,形状相似度高于60%的裂隙面网格就能较好地代表原始裂隙。当Voronoi半径为3时,基于本文方法生成的裂隙面网格能较好地代表原始裂隙,示例的体素相似度与形状相似度为66.14%和64.61%。相比于原始数据,简化后的裂隙面网格数与初始裂隙体素点数之比为约为1:39,生成的四面体网格数与图像总体素点数之比约为1:21;相比于所有体素点转换为正方体网格,生成的四面体网格与正方体网格占用存储空间之比约为1:59。 c.随着Voronoi半径的增大,虽然数据量能被进一步降低,但一些宽度或长度较短的裂隙将更容易被简化掉,从而造成形状相似度进一步下降。当Voronoi半径大于等于5后,示例的形状相似度已经小于60%,基于本文方法生成的裂隙面网格仅能代表原始裂隙中较为明显的裂隙。
1.2 相似度计算
2 实际应用

3 结 论

