潜江凹陷GH地区盐岩强反射屏蔽下砂体识别方法研究

张水山,李铭华,罗 兵,张道洪,易小芹,张 磊,李 琼,岳 林

(1.中国石化江汉油田分公司 勘探开发研究院,武汉 430223;2.成都理工大学 地球物理学院,成都 610059)

由于江汉盆地沉积在古气候时期属于强蒸发环境,潜江凹陷GH地区沉积盐岩发育。潜江凹陷自西北向东南依次为砂泥岩区—过渡相区—盐岩区,而GH地区属于过渡相区,存在岩性组合复杂、砂岩线错综尖灭、厚盐岩夹薄泥岩、膏泥岩中夹砂岩等情况。在地震剖面中盐岩—泥岩波阻抗差异大,易形成强反射;砂—膏泥岩波阻抗差异小,形成弱反射,从而易被上覆强反射轴所掩盖。这一现象在潜江凹陷地区广泛存在,且该地区砂体具有数量多、面积小、分布散、储层薄、砂体纵横向变化快的特点,常规的地震资料很难满足当前储层解释的要求,需要进行强反射剥离处理,以达到精细砂体解释的要求。

对于强反射屏蔽弱有效信号这一问题,许多学者进行了研究。Mallat S.等[1-2]提出的基于匹配追踪的稀疏分解方法,开创了信号自适应稀疏分解理论先河,随后被地球物理学者引入到地震勘探中。Liu J.L.等[3-5]先后使用Ricker子波和Morlet小波构建原子库,首先建立起了该方法与地震勘探的联系,提出了动态最优搜索策略,并通过先验参数约束搜索区间以减少搜索次数,提高了分解效率。张繁昌等[6-8]在Liu J.L.等[4]基础上,采用动态匹配子波库,实现了地震数据快速分解重构,并利用复数道分解对方法做了进一步改进,提高了分解速度与精度,对匹配子波进行施密特正交变换,降低了过完备匹配子波库的冗余度。陈发宇等[9]采用地震有限频带约束初始频率,提高了匹配速度。刘霞等[10]提出一种粒子群快速优化算法,用于快速搜索地震信号稀疏分解的最优匹配原子。王珺等[11]将遗传算法和正交时频原子相结合的匹配追踪,实现了快速匹配追踪,降低了分解度,提高了方法适用性。张雪冰[12]对地震信号的稀疏时频分解做了系统的研究,给出了不同稀疏分解方法的适用条件,并通过引入衰减的Ricker子波,实现了较准确的Q值估计。邓世广等[13]运用并行算法,将匹配追踪与伪Wigner-Ville分布结合,显著提升了运算效率,得到了更高时频分辨率的时频谱。印兴耀等[14]采用局部频率对小波进行频域先验约束,加快了匹配的速度。郭志伟[15]研究了时频分析在高精度地震资料处理重要环节中的许多应用。蔡涵鹏等[16]采用多参数构建Morlet匹配子波,快速精确地进行时频谱分析,在烃类检测方向取得了较好的效果。李海山等[17]采用低频原子优化过完备字典,很好地去除了煤层强屏蔽。朱博华等[18]具体地阐述了匹配追踪强反射去除时的原子构建参数的影响。张在金等[19]采用层位时间与解释子波约束冗余字典,实现了快速去除强屏蔽,并提取到了储层下方的低频伴影异常。杨午阳等[20]以雷克子波作为原子,利用最大相关性估计分解方法提高了分解性能。何峰等[21]提出了基于测井联合匹配追踪的强反射去除方法,解决了原子子波难以估计的问题。常健强等[22]利用多道匹配追踪子波分解与重构方法,对自来屯地区K21强反射层进行了剥离,提高了储层预测精度。

匹配追踪算法是一种信号稀疏分解算法,是压缩感知领域中的信号重构算法,主要用于高维数据降维和信号稀疏表示。它可以通过迭代过程逐步获取原始信号的稀疏表示,并且在迭代过程中可以进行实时处理,非常适合大规模数据处理和实时信号处理。本文通过研究地震匹配追踪分解过程中的匹配速度敏感参数与匹配精度敏感参数,不依赖于冗余字典,而是对字典精度降采样处理,进行多段强反射信号的匹配与重构,在此基础上针对性地提出了基于双精度降采样字典的分步正交匹配追踪强反射快速剥离改进算法。通过改进算法对实际资料进行强反射去除,有效去除了盐岩强反射信号并保留了储层弱反射信号,得到了更多构造信息。

1 改进正交匹配追踪方法实现[12]

1.1 正交匹配追踪原理

目前推广于地震信号分解与处理领域,基于最小二乘问题的匹配追踪算法是一种贪婪的迭代算法,其度量原子与信号匹配程度的数学工具为最小二乘解。

设原始信号为x,信号长度为L,则R(0)=x。以第k次迭代为例,其迭代过程相当于在冗余字典中寻找与残差信号最匹配的原子W(k)。即:

(1)

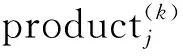
(2)

其中:W(k)为Dpos(k),是该字典中的第pos(k)处的原子。pos(k)采用下式计算:

pos(k)=jmin((Wj-R(k-1))2),j=1,2,3,…,M

(3)

但在求解每个原子的振幅系数时采用下式计算:

(4)

上式用矩阵可以表示为:

(5)

其中Φ(k)为扩充的匹配原子库,由k个原子组成,表示为:

Φ(k)=[Φ(k-1),W(k)]

(6)

A(k)为Φ(k)中的每个原子通过式求出的振幅向量,x为地震信号x(t)的向量形式,那么前k次迭代的子成分信号之和构成重构信号,为:

S(k)=Φ(k)A(k)

(7)

残差信号为:

R(k)=x-Φ(k)A(k)

(8)

由于正交匹配追踪要求所有原子Φ(k)均与剩余信号R(k)正交,即:

Φ(k)TR(k)=0

(9)

结合式(8)与式(9)可得,振幅系数向量的近似解为:

A(k)= (Φ(k)TΦ(k))-1Φ(k)Tx

(10)

值得注意的是第k-1次迭代与第k次的前k-1个原子相同,但振幅系数不相等。图1为正交匹配追踪的前两次迭代示意图。

Φ(k-1)(j)=Φ(k)(j),j=1,2,3,…,k-1

(11)

(12)

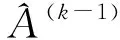
x=Φ(k)A(k)+R(k)

(13)

从图1中可以看出,在第二次迭代搜索出最佳原子后,将第二次匹配到的原子扩充到匹配原子矩阵里,此时匹配原子矩阵包含前两次迭代的最佳原子,通过匹配原子矩阵求取振幅向量,使x在W(1),W(2)所张开的平面Φ上投影最大,即S(2)最大,残差R(2)最小,第二次迭代后的残差R(2)⊥S(2)。

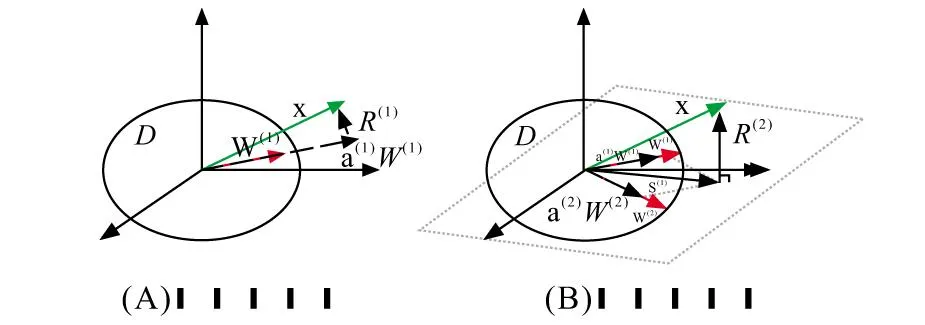
图1 正交匹配追踪算法前两次迭代示意图Fig.1 Schematic diagram of the first two iterations of the orthogonal matching tracking algorithm

1.2 方法改进

应用匹配追踪分解地震信号时,首先要构造合适的过完备时频字典。过完备时频字典通过传播时间、主频、相位等具有地球物理意义的参数来定义,并通过各种参数的精细组合,来近似的获得所有的地震子波原子。此时,字典中原子的数量远大于原子信号的长度,称为过完备字典或冗余字典。首先针对研究区GH的叠后地震数据体做了子波分析,如图2所示。

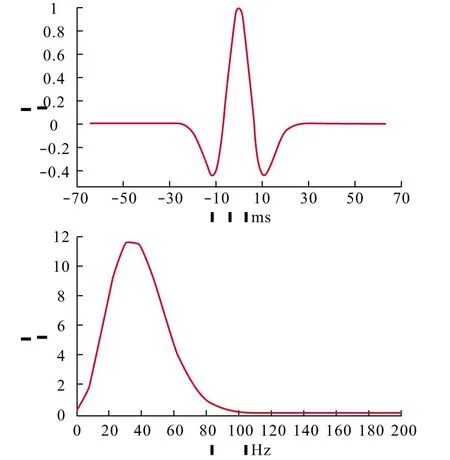
图2 子波分析Fig.2 Wavelet analysis

从地震资料中提取到如图2所示子波,为一主频31.5 Hz的零相位子波,长度约为60 ms。故本文运用Ricker子波来表征研究区地震子波。定义时频字典需许多参数,如时移、频率、相位、振幅等,这些参数既是构建稀疏字典的参数,当完全分解了地震信号后,又相当于反演了地下介质反射特征参数。理想的分解是所匹配的子波等于地下某界面所反射的子波;所匹配的原子参数等于地下某界面的反射参数。这种情况下,当匹配到强反射子波时,我们认为其就是地下强反射界面的反射子波,将该子成分信号从地震信号中减去,则完成了强反射轴的去除。那么,如何快速而准确的匹配成了关键。

常规的提升匹配精度的方法是扩大冗余字典的采样率,这种做法是最直接的提升匹配精度的方法,但却会极大的降低匹配速度。本文采用两步字典法来既快速又精确地求解最小二乘值的最优解。标准的Ricker子波为:

r(t,f)=e-(πft)2(1-2(πft)2)

(14)

其中,t表示时移,f是子波主频,子波原子采样点长度L=20。首先用时移间隔为dt=0.001 s,频率区间取30～40 Hz,间隔df=1 Hz,生成字典DⅠ。字典DⅠ按下式所示排列,其中每一个子波原子为一个列向量。

DⅠ=[r(t1,f1)r(t2,f1)r(t3,f1)…r(tLt,f1)
r(t1,f2)r(t2,f2)r(t3,f2)…r(tLt,fNf)]

(15)

其中:Lt=31为最大时移点数,Nf=11为最大频率偏移点数,故字典DⅠ为一L×Lt×Nf的矩阵。矩阵宽M=Lt×Nf=341,似乎M不满足远大于L,这是因为本文采用了两步字典法求解匹配原子,在后面构建DⅡ字典时加以解释。

用字典DⅠ对正演剖面进行匹配追踪,(正演剖面与实际剖面均为1ms采样,故在与20点的子波原子匹配计算内积时会进行降采样处理),最小二乘系数曲线如图3所示。

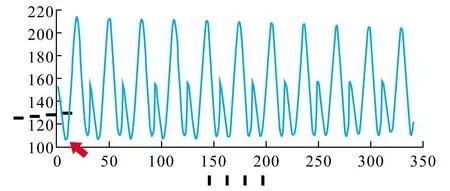
图3 最小二乘系数Fig.3 Least squares coefficient

根据字典DⅠ排列结构(公式15),可以看出最小二乘曲线对频率并不敏感,但对时移非常敏感。且由于我们的字典原子主频较低,可以认为在较小的区间内,最小曲线单调性变化不大。我们放大图3中红色箭头处的最小二乘系数最小值附近曲线,如图4所示。

从图4中可以看出,使用字典DⅠ进行匹配,最小值在第9点,此时时移间隔过大,求解精度不够。明显第9点曲线左边的梯度小于右边的梯度。故可以通过此点确定精确值所在区间为(8,10),此为1步匹配法。进一步地,在区间(8,10),增加100倍时移采样率,变为[8：0.01：10],得到临时的局部精细字典DⅡ,故本文中实际字典长度M为101×Lt×Nf,满足远大于L的要求。且在逐点内积的过程中,避免了大量在非最小值区间的计算,使得运算过程中时间复杂度更低。其最小二乘曲线如图 5中红色曲线所示。

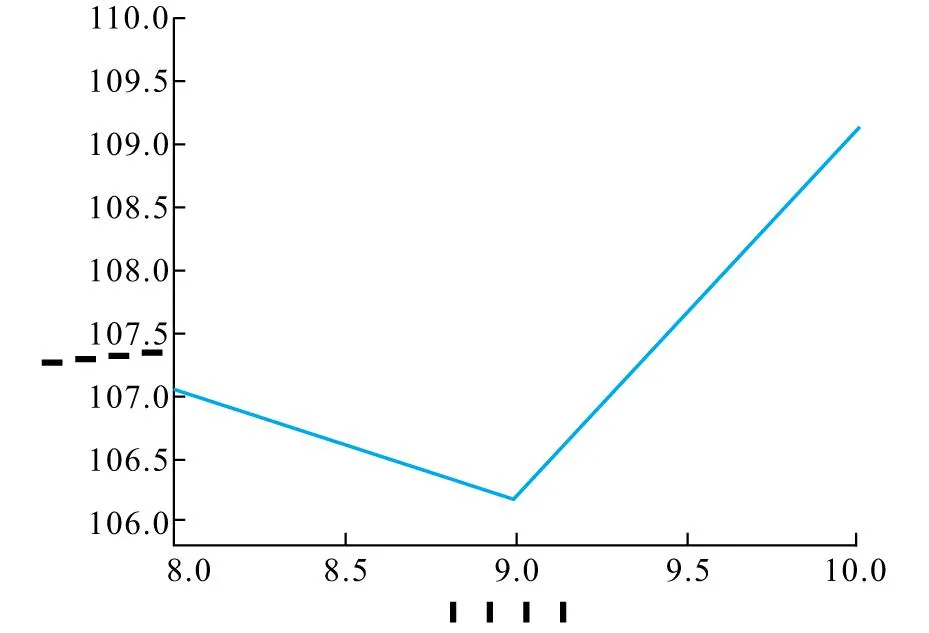
图4 最小二乘方法最小值附近的曲线Fig.4 Curve near the minimum value of the least square method

图5 改进前后最小二乘曲线对比Fig.5 Comparison of least squares curves before and after improvement

从图5中可以看出,增加采样率后,最小二乘曲线更加平滑,且出现了比点9处更小的值,其位置如图中红色点所示,其横坐标8.75为所匹配出的时移解。所匹配出的原子波形对比如图 6。

从图6中可以看出,字典DⅡ匹配到的原子相对字典DⅠ匹配到的原子有一定偏置,匹配到的原子更加准确。

图7为各道的偏置曲线,可以看出算法对各道的原子均有修正。两步法求解原子相比直接将字典DⅠ扩大100采样率更高效,计算速度更快,满足实际应用的需求。但此时方法仍存在一定的缺点,虽然此时使用的低采样率匹配强反射精度更高,但使用低采样字典生成重构信号时会出现波形被截断。如图8所示的90-100道,子波波形被截断,波形的旁瓣被“削去”,这会导致去除强反射后的剩余剖面不自然、强反射去除不干净等问题,甚至在重建剖面产生假象(图中箭头处)。通过提高重构子波采样点为41,解决了这一问题,如图9。使用41点的原子子波去除之后的剖面上,剩余的信号同相轴更连续,剩余剖面上没有出现因信号截断而产生的假象,整体比20点短时窗原子子波去除效果更好。结果表明,通过在匹配时对原信号降采样,可以减小高频成分对匹配精度的影响,提高算法稳定性与匹配速度。在恢复信号时对子成分信号恢复采样,能减小处理带来的假象。

图6 改进前后匹配原子波形对比Fig.6 Comparison of matched atomic waveforms before and after improvement

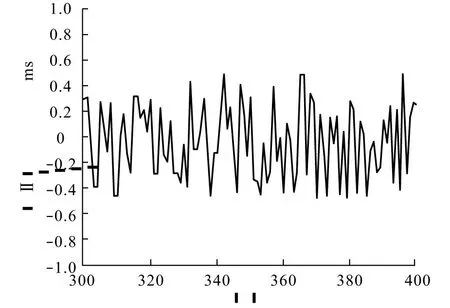
图7 相较于改进前的偏置曲线Fig.7 Compared with the bias curve before the improvement

图8 20点子波匹配的强反射Fig.8 Strong reflection of 20 dot wave matching

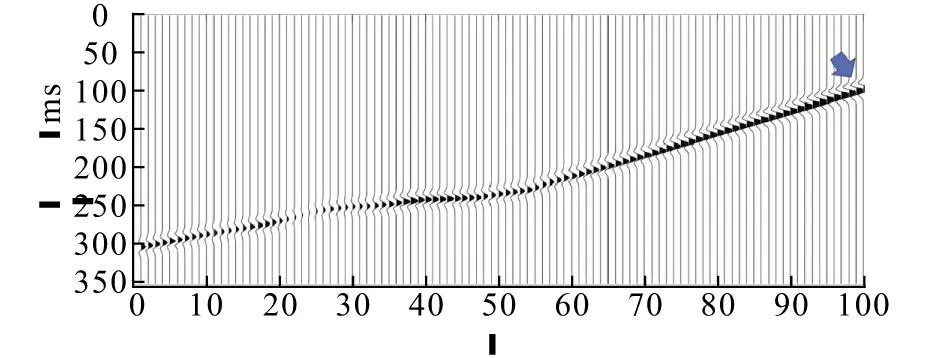
图9 41点子波匹配的强反射Fig.9 Strong reflection of 41 dot wave matching

2 应用实例

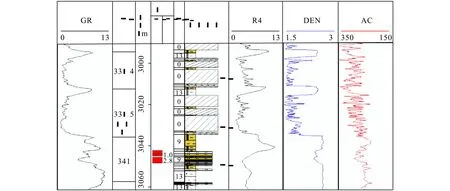
图10 Gu35井岩性解释成果Fig.10 Lithology interpretation results of Well Gu35

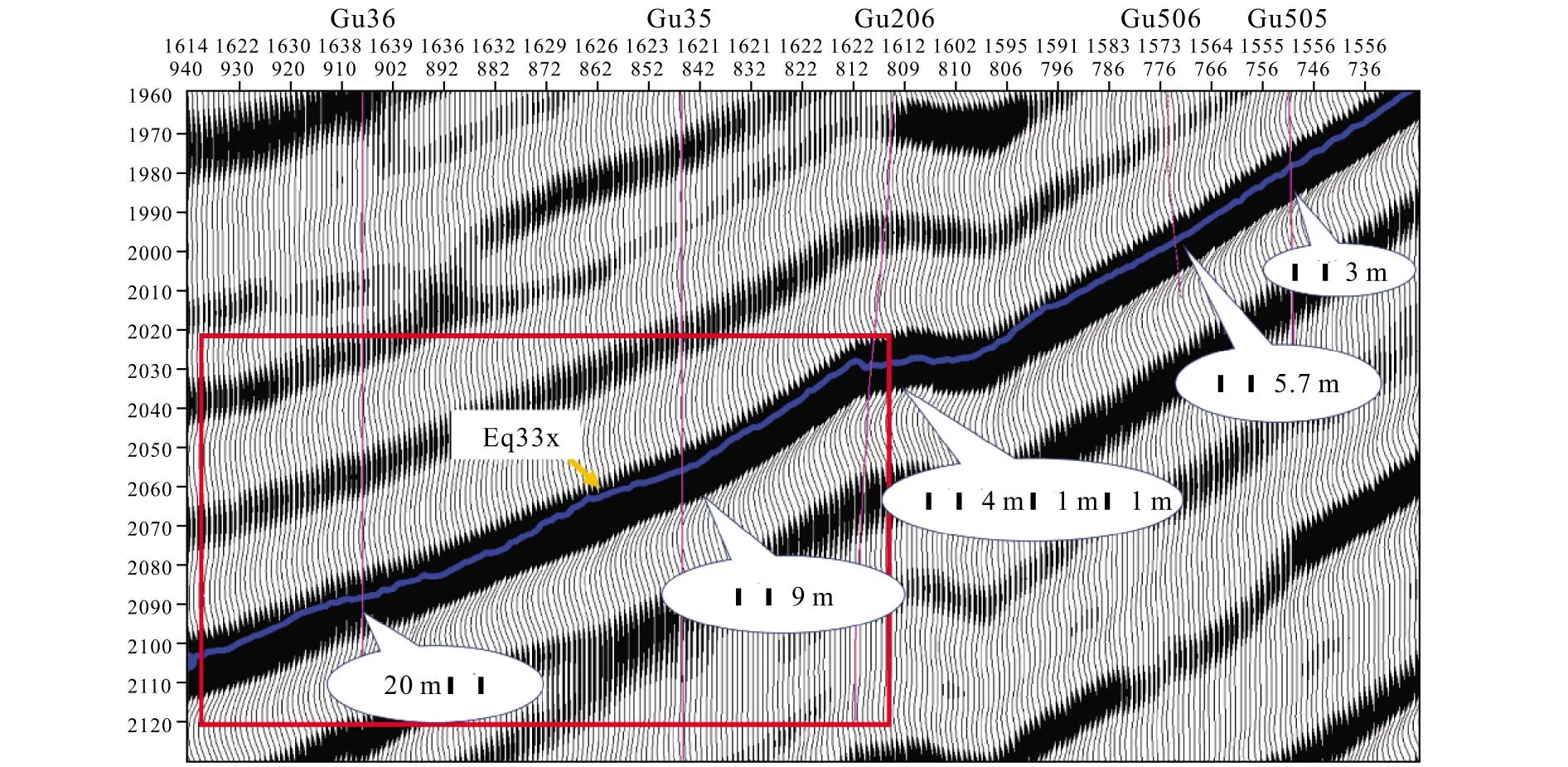
图11 实际地震剖面Fig.11 Actual seismic section

基于该方法对研究区进行强反射去除处理,如图15所示,图中红色曲线为沿有效信号波峰位置。

图12 原始剖面Fig.12 Original section

图13 高分辨率处理后剖面(45 Hz)Fig.13 High-resolution profile (45 Hz)

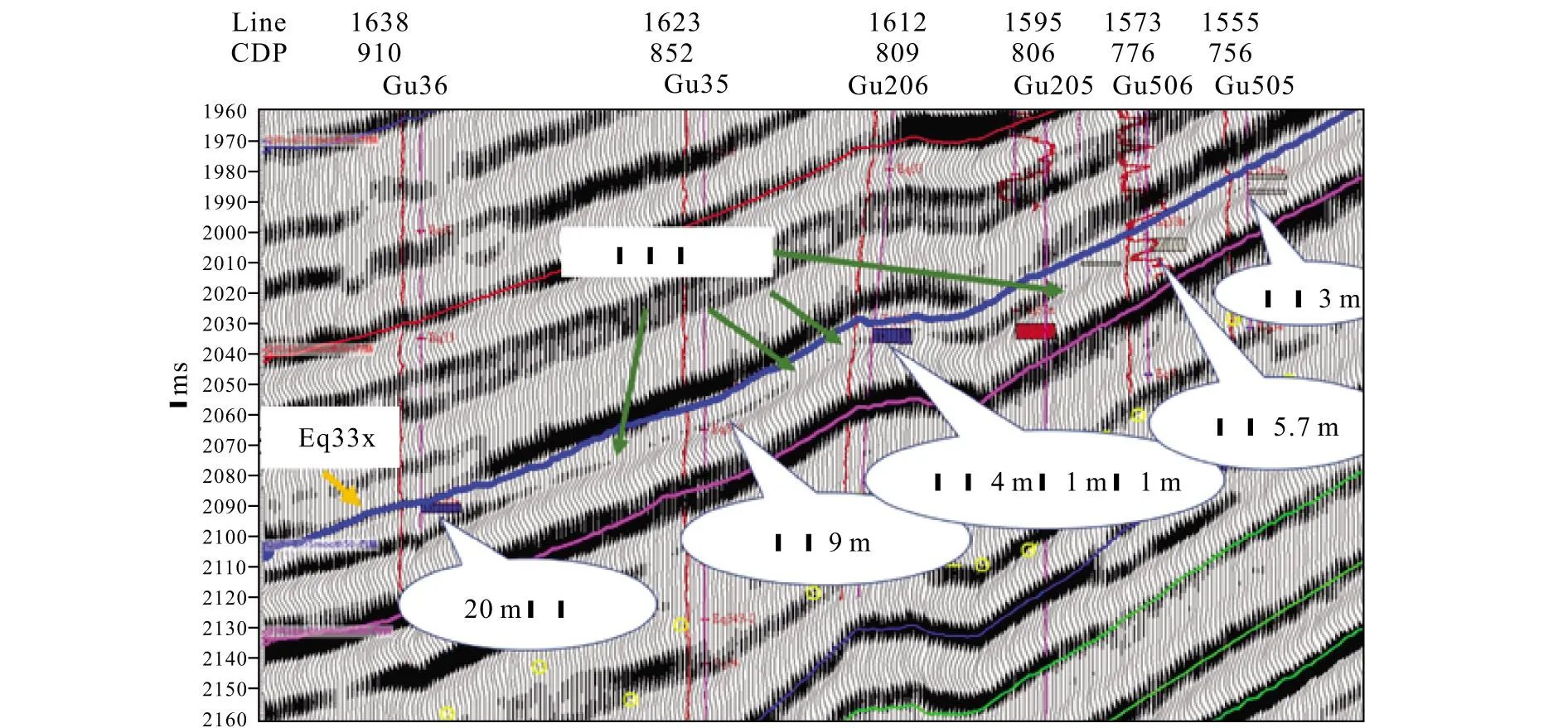
图14 盐岩强反射剥离处理后剖面Fig.14 Section of salt rock after strong reflection stripping treatment

从图16对比结果可以看出,处理前强反射屏蔽了砂岩弱信号,导致砂体平面特征不明显。通过本文方法处理后,成功显示出砂岩弱反射信号,提取的砂体平面特征明显,与钻井钻遇砂岩位置对应良好,预测吻合率达到了84.60%。

沿解释的砂体界面提取原始数据与高分辨率及强反射剥离后数据的均方根属性,得到砂体平面特征如图16。

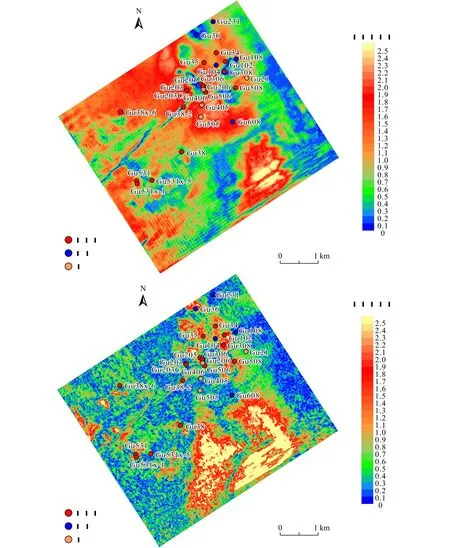
图16 处理前后均方根振幅属性对比Fig.16 Comparison of RMS amplitude attributes before and after treatment

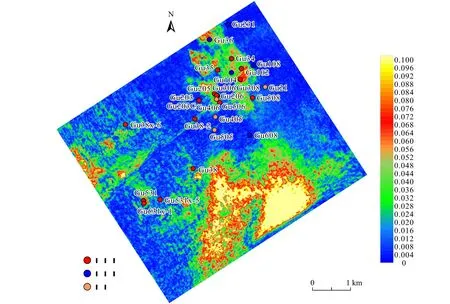
图17 强反射剥离后砂体流体检测平面属性Fig.17 Fluid detection plane properties of sand body after strong reflection stripping

3 结 论

a.本文基于最小二乘优化的正交匹配追踪算法进行研究,对GH地区盐岩强反射屏蔽储层有效信号的难题进行分析研究。利用地震资料,详细分析了原子字典构建参数:采样率、时移、频率、相位、振幅对匹配速度与匹配精度的影响。提出基于双精度降采样字典的分步正交匹配追踪强反射快速剥离改进算法,减小了在非最优解区间的匹配运算,兼顾了匹配速度与精度,提高了算法稳定性。