案例教学模式下的稀疏矩阵的概念与应用

许春荣　买买提依明·哈斯木

【摘  要】 矩阵在数据存储、机器学习、图像处理、自然语言处理中有着广泛的应用。稀疏矩阵是指矩阵中非零元素的个数较少的类型。数据结构这门课程作为高校计算机基础的一门课程，主要介绍的是计算机科学中用于组织和管理数据的方法和技术，其中包括介绍稀疏矩阵的内容。目前，一些教材在数据数组存储介绍上，对稀疏矩阵这个章节内容讲解较少，仅为理论内容，有些具体应用没有叙述清楚，容易使学生理解不深。为此，文章介绍具体案例，讲解稀疏矩阵的存储特点以及在计算效率上的优越性，让学生更好地理解稀疏矩阵，也更好地掌握数据结构这门课的内涵。

【关键词】 数据结构；稀疏矩阵；计算效率

数据结构是高等学校大部分理工类专业本科学生在学校必须完成的基础课程。数据结构课程主要介绍的是计算机科学中用于组织和管理数据的方法和技术。它涉及存储、组织、操作和检索数据的不同数据结构和算法的设计和分析。通过学习数据结构课程，学生可以培养良好的问题分析与解决能力，提高程序设计和算法实现的效率，为进一步学习计算机科学的相关课程打下坚实的基础。学生对该课程的掌握情况将影响到后续专业课程的学习及逻辑思维方式和程序设计思想的建立。在数据结构中，数组的存储是重要的内容，其中包括特殊矩阵——稀疏矩阵存储。

目前，一些教材在数据数组存储介绍上对稀疏矩阵这个章节内容讲解较少，主要介绍稀疏矩阵的压缩存储方式，一些具体应用没有叙述清楚，容易使学生理解不深，为此，需要在教学中对稀疏矩阵加以介绍，适当地加一些计算机案例教学，设计案例讲解稀疏矩阵的概念。本研究将通过一些例题实验对稀疏矩阵在存储和计算上进行介绍，并和一般稠密型矩阵进行比较，对比介绍稀疏矩阵的特点和优越性。

一、稀疏矩阵

稀疏矩阵在数据存储、机器学习、图像处理、自然语言处理以及工程上有着广泛的应用。稀疏矩阵是指在一个二维矩阵中，绝大部分元素都是零的矩阵。与稠密矩阵（大部分元素非零）相比，稀疏矩阵的特点是具有较少的非零元素，占据整个矩阵的很小一部分（一般小于5%）。稀疏矩阵的应用方面有很多，包括在线性代数上，如矩阵运算、求解线性方程组、特征值计算等。

在图论和网络分析中，稀疏矩阵常用于表示图结构、网络连接等。在自然语言处理中，稀疏矩阵常用于文本特征表示和文本分类任务。在图像处理中，稀疏矩阵常用于压缩和图像恢复任务。例如压缩感知技术利用稀疏矩阵表示图像，可以实现高效的图像压缩和重建。常见的稀疏矩阵有带型阵，块三角，块对角阵，单面镶边的带型阵，双面镶边的带型阵等。由于稀疏矩阵它的特点，可以从存储上对矩阵的运算做一些描述，以便更好理解稀疏矩阵。

已有较多学者对稀疏矩阵的存储进行研究，焦点在于设计合适的存储结构，并在此基础上进行高效的稀疏矩阵运算。

存储矩阵的一般方法是采用二维数组，其优点是可以随机访问每一个元素，因而能够实现矩阵的各种运算。但对稀疏矩阵而言，会重复存储多个无效元素，这浪费了内存空间，而且不方便查看有效数据的位置，花费大量时间来进行行列元素的无效计算。所以必须考虑对稀疏矩阵进行压缩存储。稀疏矩阵的压缩存储方式有多种，主要有以下几种：

1. COO（Coordinate）格式。COO格式使用三个数组分别存储非零元素的行坐标、列坐标和对应的数值。

2. CSR（Compressed Sparse Row）格式。CSR格式是常用的稀疏矩阵存储压缩格式。CSR格式使用三个数组分别存储非零元素的数值、列索引和行指针。行指针数组记录每行第一个非零元素在数值数组中的位置索引。这种格式适用于按行访问稀疏矩阵的情况，可以高效地存储和计算稀疏矩阵。

3. CSC（Compressed Sparse Column）格式。这种格式和CSR相同，只是矩阵元按列压缩存储，CSC使用三个数组分别存储非零元素的数值、行索引和列指针。列指针数组记录每列第一个非零元素在数值数组中的索引位置。这种格式适用于按列访问稀疏矩阵的情况。

4. DOK（Dictionary of Keys）格式。DOK格式使用一个字典（键—值对）来存储非零元素的位置和数值。字典的键表示元素的行列索引，值表示对应的数值。这种格式适用于动态稀疏矩阵或矩阵结构频繁变化的情况。

5. BSR（Block Compressed Sparse Row）格式。BSR格式将稀疏矩阵分为固定大小的块，并对每个块存储非零元素的数值、列索引和块指针。这种格式适用于拥有块结构的稀疏矩阵。

不同的稀疏矩阵表示形式具有不同的优势和适用场景。选择合适的表示形式可以最大限度减少存储空间的使用和提高矩阵操作的效率。本文主要采用第一种存储方式COO（Coordinate）格式进行存储。COO使用三个数组分别存储非零元素的行坐標、列坐标和对应的数值，是一种三元组顺序表压缩存储方式。当一个数组中大部分元素为0，或者为同一个值的数组值，可以使用三元组顺序表来保存该数组。稀疏数组的处理方法是把具有非零值的元素的行列记录在一个三元组的顺序表中，每个数据元素都是以三元组的方式组成的，即（i，j，aij），其中i表示行，j表示列，aij表示元素。利用三元组存储，可以减少存储空间，这样矩阵以小规模的数组存储，从而缩小程序的规模。

二、稀疏矩阵的案例设计

稀疏矩阵是一种特殊的矩阵，由于跟一般矩阵有着不同的特点，学生的学习理解比较浅层，为了让学生能在学习中对稀疏矩阵有更好的理解，教师可通过设计一些案例进行讲解，让学生理解更透彻。案例设计主要包括稀疏矩阵的存储以及计算效率的特点介绍。

（一）稀疏矩阵的存储特点

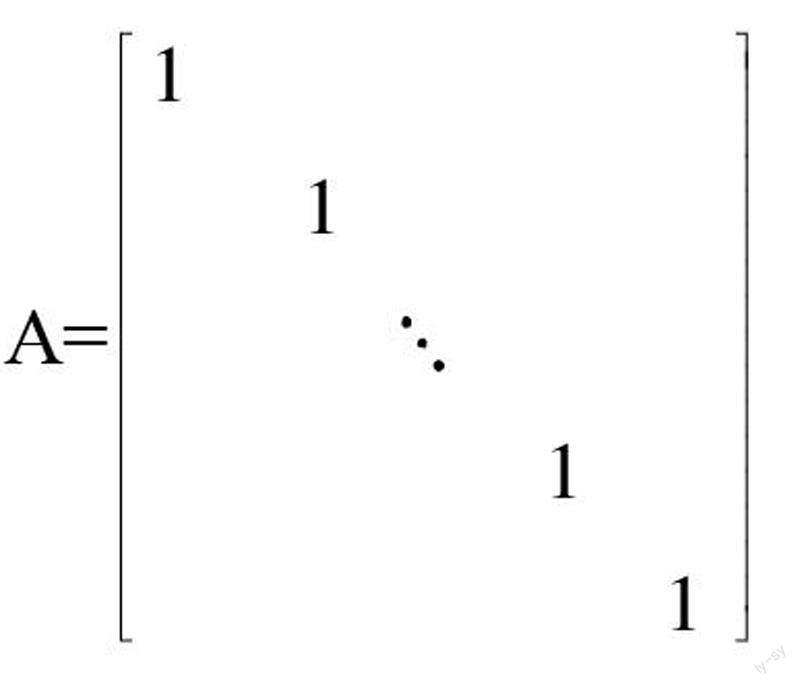
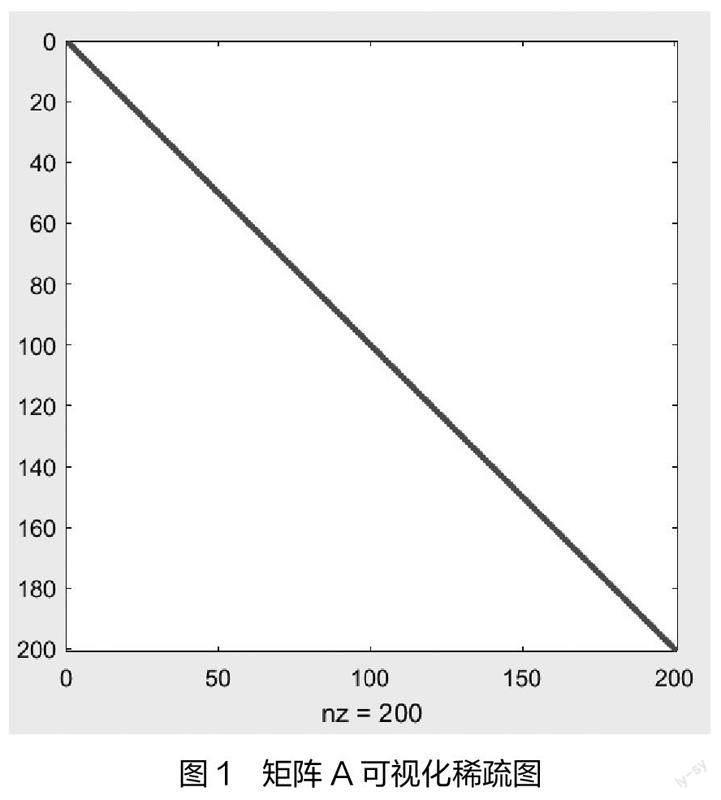
例1：设A为一个200*200的单位矩阵。

其稀疏程度如图1所示。

此时A为稀疏矩阵，利用稀疏数组形式存储，即利用三元组顺序存储，如表1。

查看两个矩阵的存储空间，原矩阵存储，稀疏矩阵数组存储空间大小对比如表2所示。

从结果可以看出，以稀疏矩阵三元组顺序表存储，存储空间为4808bit，以一般矩阵形式存储为320000bit，以一般矩阵存储占用的空间是以三元组顺序表存储空间的66倍，可见，稀疏矩阵采用三元组顺序表存储的方法可以大大节省存储空间。

（二）稀疏矩阵在计算上的特点

稀疏矩阵在加法、乘法上以及一些特征值的计算有着更高的效率。下文通过案例介绍。

例2：求解稀疏矩阵的特征值，A为1000*1000的矩阵，除了三条对角线为1外，其余都为0，这里对A矩阵求特征向量值，再用稀疏矩阵数组形式求解特征值。

利用Matlab编程运算，得到运行结果，从运行结果可以看出，利用原矩阵和稀疏数组形式计算出来特征值一样，而在计算时间上，一般形式矩阵计算为0.0115s，利用稀疏矩阵求解特征值为0.0115s，这说明采用稀疏数组的形式计算特征值速度也会更快，更加节省时间。稀疏矩阵在逆矩阵的求解上也具有较快的速度，如例3。

例3：设A矩阵为可逆稀疏矩阵，采用稀疏数组方式进行求逆，并与一般形式矩阵形式求逆矩阵做对比。

利用Matlab运算，得到运行结果，从结果看出，若矩阵A为稀疏矩阵，采用稀疏数组形式以及一般形式矩阵，对其齐求逆矩阵，求得的解都一样，而其求解的速度原矩阵计算时间为0.0183s，稀疏数组计算需要的时间为4.7550e-04s，用稀疏数组计算逆矩阵速度要快于一般形式矩阵求解逆矩阵，可见稀疏数组在求解上有更高的效率，还可以应用一些数学知识求解。另外，在求解方程组时，稀疏矩阵在计算上效率也更高，如例4。

例4：设A矩阵为三对角矩阵，Ax=b；采用稀疏数组方式进行求逆，并与一般形式矩阵求解方程组做对比。

利用Matlab运算，得到运行结果。从运行结果可以看出，利用一般形式矩阵和稀疏矩阵形式计算出来方程组的解是一样的，而在计算时间上，一般形式矩阵计算为0.0780s，利用稀疏数组求解特征值为7.0070e-04s，可见用稀疏数组的形式计求解方程组速度会更快，效率更高。

三、结语

稀疏矩阵作为一种特殊矩阵，在数学上、工程上有較好的运用，本研究通过列举案例介绍稀疏矩阵的存储和计算，对稀疏矩阵的介绍进一步补充说明，可以较好地理解稀疏矩阵的稀疏数组形式与一般矩阵形式在存储上和计算上的区别。从例子的结果可以看出，稀疏矩阵数组形式在存储上可以较地好降低存储空间，而在计算上，包括稀疏矩阵的特征值，逆矩阵的计算以及求解方程组上都有较高的效率。通过这样的例子，学生可以对教材中稀疏矩阵有更好的理解。由于稀疏矩阵的特点，在工程上，比如机器学习，图像处理，文本分类上，如果矩阵为稀疏矩阵，那么可以采用稀疏矩阵数组形式进行存储和计算，从而减小存储空间，提高处理效率。稀疏矩阵在存储和计算上具有优越的特点，如果是非稀疏矩阵，即矩阵在高数据密度（50%以上）下，一个完整的矩阵总是比一个稀疏的矩阵快，所以教学时要根据矩阵的具体特点，做相应的处理，以更好地提高效率。

参考文献：

［1］ 严蔚敏，李冬梅. 数据结构（C语言版）（第2版）［M］. 北京：人民邮电出版社，2021.

［2］ 李向华，王震，高超. 面向数据结构的“C程序设计”教学改进策略［J］. 西南师范大学学报（自然科学版），2023，48（05）：111-115.

［3］ 曹中潇，冯仰德，王珏，等. 基于深度学习的稀疏矩阵向量乘运算性能预测模型［J］. 计算机工程，2022，48（02）：86-91.

［4］ 李佳佳，张秀霞，谭光明，等. 选择稀疏矩阵乘法最优存储格式的研究［J］. 计算机研究与发展，2014，51（04）：882-894.

［5］ 张玉州. “数据结构”课程中稀疏矩阵运算器的实现［J］. 安庆师范大学学报（自然科学版），2017，23（01）：98-101.

［6］ 薛红涛，丁殿勇，李汭铖，等. 基于分量加权重构和稀疏NMF的轮毂电机轴承复合故障特征提取方法［J］. 机械工程学报，2023，59（09）：146-156.

［7］ 杨凡，饶雨泰. 基于双向稀疏的多视图子空间学习算法［J］. 计算机应用与软件，2023，40（06）：266-275.

［8］ 包世鹏，宋旭明，唐冕. 基于向量化的BESO方法灵敏度过滤快速算法［J］. 铁道科学与工程学报，2023，20（05）：1810-1820.

［9］ 郑慧敏，郑明洁，张振宁，等. 基于低秩和一维稀疏矩阵分解的多通道SAR-GMTI方法［J］. 中国科学院大学学报，2022，39（02）：208-216.

［10］ 顾越，赵银亮. 基于RISC-V向量指令的稀疏矩阵向量乘法实现与优化［J］. 计算机工程与科学，2022，44（01）：1-8.