地震激励下大型储罐内液体晃动响应分析

梁俊杰，王琼瑶，林国勉，徐 凯

（五邑大学智能制造学部，广东 江门 529000）

0 引言

液体晃动是在有限空间内受到外部激励后具有自由液面的流体的运动[1]。由于其强大的非线性和随机性，它一直是许多研究的焦点，特别是在航空航天、陆海运输工程和液体储存领域。以储油罐为例，储油罐通常被视为刚性的，一般用于储存石油或其他化学液体产品，这类储液通常易燃或有毒。储罐中的储存液体晃动会给储罐壁带来额外的力，并冲击储罐顶部，这可能会导致储罐结构破坏和无法正常使用。严重情况下，储存的液体会泄漏[2]，这可能会污染周围环境，甚至引发火灾。为了减少这种情况，一种方法是降低储罐的液体填充率，并为储罐中的存储液体保留足够的振动空间，以有效地减少储罐顶部受到的冲击载荷，但这将导致储罐的利用率不足，对于较大的储罐经济性较差。相比之下，在储罐中安装挡板[3]、浮板[4]和弹性气囊[5]等阻尼装置可以减少流体冲击载荷。其中，挡板由于其安装简单、抑制液体晃动的效率高而被公认为最常用的防晃装置。因此，研究挡板参数对液体晃动固有特性的影响是一个非常有意义的课题。

1 液体晃动研究方法的发展

对于充液容器，由其满足不同理论下建立的控制方程，通常可将液体晃动的研究方法分为两类：一类是基于势流理论的分析方法。Abramson[6]对各种规则几何形状（包括矩形、环形、圆柱体等）储罐中的液体晃动进行了系统研究，应用线性势流理论分析了横向微晃动下储罐中储存的液体。Hasheminejad[7]对二维半充液刚性椭圆储罐进行了晃动分析，并利用连续保角技术和势流理论推导了一套计算带有垂直挡板的椭圆储罐固有振动特性的公式。

一般而言，分析方法适用于结构简单且晃动幅度较小的情况，而数值方法适用于不规则储罐形状且晃动幅度较大的情况。此外，数值方法也可用于研究具有各种阻尼装置（如挡板、浮板等）的储罐中的液体晃动。根据控制方程的不同离散化方法，数值方法可分为有限元法（FEM）、有限差分法（FDM）、有限体积法（FVM），边界元法（BEM），光滑粒子流体力学（SPH）。

Biswal 和Bhattacharyya[8]使用FEM 评估了液体和储罐-挡板系统的耦合响应，研究了不同参数（如复合挡板、层压方案）对液体填充复合储罐中晃动频率和耦合振动频率的影响。Ünal 等[9]应用FDM 研究了封闭的二维部分填充矩形储罐中的液体晃动，并比较了T 形挡板和无挡板储罐中的晃动情况，结果表明，当挡板的高度大于液位的80%时，挡板在压力和波浪阻尼方面完全有效。Chen Yang[10]采用FVM 方法和Lattice Boltzmann 方法相结合的方法对不同容器设计下的液体晃动行为进行了快速评估，结果表明，LBM 模型的计算时间开销仅为FVM 模型时间开销的7.0%左右，且不影响数值精度。Cho 等[11]应用BEM 获得了多孔水平挡板晃荡的解析解，考虑了矩形储罐中心和两侧壁的两个挡板位置，以确定不同的孔隙率、长度和浸没深度。结果表明，与安装在储罐中心的水平多孔挡板相比，安装在两个储罐壁上的水平多孔隔板显著抑制了剧烈的共振晃动响应。McNamara[12]提出了二维显式不可压缩SPH 模型，用于研究安装在调谐液体阻尼器内的矩形储罐中的液体晃动响应。发现SPH 模型与TLD 储罐尺寸范围内的实验数据非常吻合，可进一步用于研究矩形TLD的非线性响应。

除了上述用于研究液体晃动现象的分析和数值方法外，实验方法是一种直接的方法。Chia Ren Chu 等[13]使用LES 模型研究了矩形水箱中的晃动，并通过添加多个底部挡板测试了其抑制晃动的能力。实验结果表明，多个挡板对水动力的抑制效果优于单个挡板。多个挡板可以改变容器的固有频率。防晃效果将随着挡板数量和高度的增加而增加。当挡板的相对高度大于0.75 时，挡板对晃荡的影响将减小。T.Nasar和Sannasiraj[14]分别在罐壁的l/3 和21/3 处安装了孔隙率分别为15%、20.2% 和25.2%的挡板，测试了它们在规则束激励下的晃动动力响应，并讨论了这些挡板方案的有效性和驳船效应。

本文建立了一个基于FVM 的数值模型来研究直立圆柱形储罐中的液体晃动现象。由于二维模型获得的模拟结果的精度与三维模型相当[15]，本文采用了二维模型，该模型模拟了直立圆柱形储罐的最大横截面。根据对自由液面、动态晃荡力和施加在罐壁上关键点的冲击应力的评估，提出了几种挡板配置，以研究其对地震激励下液体晃荡的防晃荡效果。

2 理论背景

2.1 控制方程

基于OpenFoam 进行液体晃动模拟。OpenFoam 是基于FVM 的开源软件。由于封闭罐中晃动液体的速度较低，可采用层流模型。忽略液体的压缩，封闭罐中的控制方程为：

式中：∇为哈密顿量；u→为速度；ρ为液体密度；p为压力；为部分黏性应力张量，（式中：μ为动态黏度，S为平均应变率张量，S=，且I=δi）j；fb为身体力。数值模拟采用了气相和液相两相流模型。

基于流体体积（VOF）方法捕获两相之间的界面，该方法需要定义指数函数，并需要了解界面是单独被某一流体占据还是同时被两种流体占据，这需要求解相分数方程。

式中：α为每个单元的液相分数。α=0表示网格完全被气体占据；α=1 表示网格完全被液体占据；而0 ＜α＜1 表示细胞同时被气相和液相占据，即网格位于气相和液相的界面。

每个网格区间的密度、速度等物理性质由网格的液体体积分数计算，其方程为：

式中：αc为每个细胞液体的体积分数；ρl为液体的密度；ρa为气体的密度；v为运动黏度；vl为液体的运动黏度；va为空气的运动黏度。

2.2 OpenFoam 及其求解器interFoam

使用OpenFoam 中的两相流求解器“interFoam”与动态网格技术一起解决储罐中液体的晃动情况。模拟实验首先会将罐壁设置为移动边界，将地震激励下的移动理想化。对于临界自由曲面，求解器基于VOF 理论方法中的网格重建和方程执行变形捕捉。压力-速度耦合问题通过PIMPLE 算法解决，该算法结合了PISO（压力隐式算子分裂）和SIMPLE（压力关联方程的半隐式方法）。

2.3 模型创建

为研究地震运动作用下储罐中液体的晃动以及各种阻尼挡板配置的防晃效果，本文采用一个实际尺寸的工业容器进行了模拟实验。尺寸如图1、表1所示。

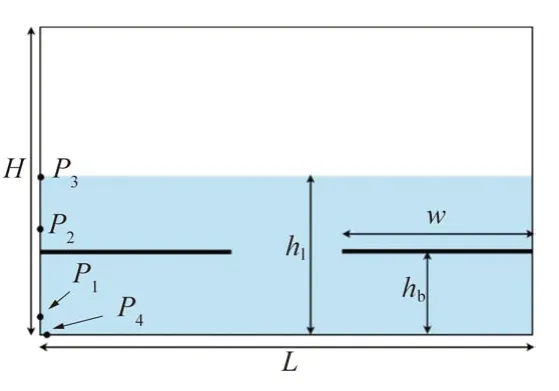
图1 立式储罐的最大横截面图

为了分析储罐在真实地震运动下的晃动，本次模拟选择了kocaeli 波[16]。如图2 所示，该地震数据选自Yarimca（YPT060）平台，该长周期地面运动根据地面加速度进行缩放。最大加速度为1.32 m/s2。为了确保模拟符合实际情况，选择晃动液体作为原油，密度为857 kg/m3，运动黏度为0.000 032 m2/s。

图2 地震加速度变化情况

如图1 所示，在左侧罐壁和罐底设置了4 个监测点。监测点P1至P3用于监测地震运动下罐壁压力随时间的变化，P1至P3相对于罐底的高度分别为9.0、6.0 和1.0 m。P4是波高监测点，用于分析左侧罐壁附近自由面高程的时程。为了研究环形挡板配置对液体晃荡响应的防晃荡效应，在模拟中考虑了具有不同相对宽度（挡板宽度与储罐半径之比，w/R）和相对安装高度（挡板高度与静态时液体高度之比，hb/hl）的环形挡板。选择了4 种不同的相对宽度，即0.21、0.32、0.49和0.72，相对安装高度选择为0.39、0.50、0.61、0.72、0.83 和0.94。在不同的挡板配置下，比较了晃动响应，如监测点处的压力、施加在罐壁上的动态晃动力、自由表面位移的评估，以研究其防晃动效果，并最终找到最合适的挡板配置。

3 采用不同挡板方案的储罐中油液晃动特性的数值分析

3.1 自由液面变化

通过保持一个参数不变ua 改变另一个参数的方式研究了挡板的相对宽度和相对安装高度对自由液面变化的影响。将带不同挡板的储罐与不带挡板的储罐的仿真结果进行了比较。

图3 显示了具有不同相对挡板宽度和相对安装高度的折流板储罐和空罐的最大波高。当挡板相对宽度超过0.32 时，随着挡板相对安装高度的增加，最大波高显著降低，而当挡板相对高度小于0.32 时（挡板相对安装深度从0.39增加到0.83），最大波高也随之降低。然而，随着挡板宽度的进一步增加，最大波高显著增加，这是因为挡板宽度太短，无法覆盖液体晃动的波峰，从而导致波峰和挡板边缘发生碰撞。

图3 波高峰值变化

为了更具体和直观地表达每种挡板配置的晃动抑制效果，引入了波高抑制率的概念，可用式（6）表达。

式中：η0为空罐的最大波高；η为安装折流板后的最大波高；δ为波高抑制率。

图4 为各种挡板配置下的波高抑制率。对于相对宽度为0.72的挡板，当挡板相对安装高度在0.39～0.94范围内时，波高抑制率为5%～10%，而对于相对宽度0.21、0.32 和0.49 的挡板，相应的波高抑制率分别为0.5%～6.4%、2%～6.5%和3.5%～7.5%。从图中可以看出，除了挡板宽度小于0.32的情况外，随着挡板安装高度的增加，波高抑制率增加。这意味着，当立式圆柱形储罐中挡板的相对宽度大于0.32，挡板越靠近液体自由表面，挡板的防晃荡效果更加明显。此外，从图中可以看出，当挡板相对安装高度从0.83 增加到0.94 时，相应的波浪抑制率呈现缓慢增长。因此，折流板直立圆柱形储罐的最佳相对安装高度在0.72～0.83之间。

图4 波高抑制率

3.2 壁面上的压力变化

图5 为各种挡板配置下施加在左壁上压力的最大值。可以看出，对于不同相对宽度的挡板，随着相对安装高度的增加，施加在左侧罐壁上的力的最大值增加，尤其是当挡板接近液体自由表面时。这是由于挡板的添加确实限制了晃动幅度，但同时限制了动能转化为重力势能，从而导致动态晃动力的增加。这意味着折流板具有显著的阻尼效应。此外，对于具有给定相对宽度的挡板，相对安装高度越大，压力减少所需要的时间越短，这意味着挡板的阻尼效应对于安装高度较高的挡板更明显。其原因是液体和挡板之间存在相互作用。相对地，挡板的阻尼效应能使压力更快地达到稳定状态。

图5 压力峰值变化

3.3 关键点的冲击应力变化

监测点P1 设置在相对高度为0.11（相对于液体高度hl）的较低位置，因为挡板的最低相对安装位置为0.39，这使其始终位于挡板下方。图6 显示了各种挡板配置下P1 的峰值压力。从图中可以看出，除非其接近自由表面，挡板相对安装高度的变化只对压力峰值有轻微影响。相对地，挡板相对宽度对压力峰值有很大影响。随着挡板宽度的增加，压力峰值急剧增加。如图7 所示，地震激励在30 s时停止，储罐中的液体晃动可视为自由振动，这可以证明各种挡板的阻尼效果。图7 显示了地震激励停止后P1处的压力峰值，当挡板相对宽度处于较低水平时，P1 处的峰值压力随着挡板安装高度的增加呈线性下降。当挡板宽度足够大时，挡板安装高度对P1处压力峰值的影响是有限的。

图6 P1的峰值应力

图7 地震激励结束后P1的峰值应力

与P1 不同，监测点P3 被设置在相对高度为1.0（相对于液体高度hl）的位置，这使得它总是在挡板上方。图8 为不同挡板配置下P3 处的峰值压力值，结果表明挡板相对宽度和安装高度对P3 处的压力峰值有显著影响。当挡板安装高度从0.83 增加到0.94 时，P3 处的峰值压力值反而在一定程度上增加，这是因为存在挡板，与图3所示的峰值自由表面评估的情况一致。

图8 P3的峰值应力

图9 为地震激励停止后P3 处的压力峰值，因为挡板始终低于监测点P3，无论挡板高度如何，挡板宽度对P3处的峰值压力变化有轻微影响。相对地，挡板的相对安装高度对该点的峰值压力有显著影响，随着挡板安装高度的增加，P3处的峰值显著降低。

图9 地震激励结束后P3的峰值应力

图10 显示了各种挡板配置下P2 处的峰值压力值。监控点P2 不同于点P1 和P3，它被设置在相对高度为0.67（相对于液体高度hl）的位置。根据挡板的安装位置，监控点并不总是在挡板上方。从图中可以看出，随着安装高度的增加，P2 处的峰值压力几乎以线性方式降低，除了挡板从监控点下方的位置转移到监控点上方的位置以外，即相对安装高度从0.61 增加到0.72 时，P2 处的峰值压力显著地提高了。图11 显示了地震激励停止后挡板配置对P2 峰值压力值的影响，与P1 和P3 的情况类似，峰值压力值随着挡板安装高度的增加而减小，然而，当挡板相对安装高度达到0.72 时，随着挡板安装高度的进一步增加，峰值压力值几乎保持恒定。

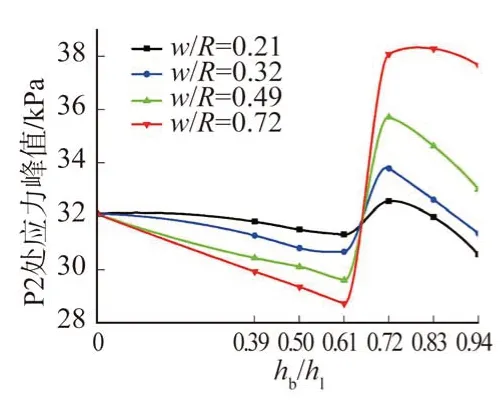
图10 P2的峰值应力

图11 地震激励结束后P3的峰值应力

4 结束语

本文模拟分析了Kocaeli 地震波激励下立式储罐在最大垂直截面处的晃动行为。使用基于FVM 数值方法的OpenFoam 平台建立2D 模型，采用VOF 方法和动态网格技术捕捉了液-气两相界面。实验中储罐模型和挡板都被假设为刚性的。分析表明，挡板的相对宽度和安装高度对液体晃动有显著影响。

（1）当挡板接近液体自由表面时，只要挡板的相对宽度大于0.32，挡板的防晃效果就非常明显。

（2）挡板的添加使得液体在晃动过程的初始阶段更频繁地振荡。之后，挡板的阻尼效应使液体更快地达到稳定状态。

（3）随着相对安装高度的增加，施加在左罐壁上的力的最大值增加，特别是当挡板接近液体自由表面时。这是因为添加挡板确实限制了晃动幅度。

（4）随着安装高度的增加，监测点的峰值压力几乎呈线性下降。并且位于挡板上方的监测点的峰值压力明显大于挡板下方的监测点。

（5）在地震激励下，折流板立式圆筒形储罐的最佳相对安装高度为0.72～0.83。