探针型线对汽车空调用二氧化碳可调喷射器性能影响的仿真研究

曾宏轩 赵红霞

（山东大学，济南 250012）

1 前言

随着温室效应不断增强，环境更加友好的CO2等天然制冷剂越来越受国际社会重视，CO2循环制冷系统已经在汽车空调[1]、超市制冷系统[2]等领域取得了较为成功的应用。CO2具有单位容积制冷量高的优点，作为制冷剂被应用在空间狭小的电动汽车内，效果较为优异。同时，由于汽车空调的冷凝器采用风冷方案，风温与环境温度相关，所以冷凝温度往往高于CO2的临界温度，因此通常采用CO2跨临界循环。喷射器作为降低节流损失、减少压缩机压比的部件，在汽车空调CO2制冷系统中具有重要的实用意义。李浩等[3]对汽车空调用CO2制冷系统进行了研究，结果表明，在不同工况下，喷射器能使系统的制冷系数（Coefficient Of Performance，COP）提高1.65%～12.60%。

但固定结构喷射器只有在设定工况下才拥有较高的效率，因此，可调喷射器近年来得到了充分的发展，许多学者对其性能进行了研究。Galindo[4]等通过数值计算的方法，对比了固定式喷射器和可调式喷射器，证明了使用可调式喷射器的制冷系统的COP 更高。Li[5]证明了采用变面积比喷射器的制冷系统比使用压力调节阀的制冷系统能效高12%以上。

均相平衡模型（Homogeneous Equilibrium Model，HEM）[6]假定流体在两相区处于热力学和力学平衡状态，流体被视为介于液态和气态的中间态，密度、粘度等物性随着干度的变化而变化[7]。在CO2喷射器领域，HEM 已经被证实为一种可有效处理两相流流动的模型。Lucas[8]在OpenFOAM 中将基于HEM的仿真结果与试验结果进行了对比，结果表明，HEM预测的最大误差可以达到20%。

目前，关于可调喷射器的研究着重于性能及其在不同工况下的表现，对于探针本身的研究较少。本文基于HEM 提出3 种探针型线方案并进行对比，以获得合适的汽车空调用CO2可调喷射器的探针外型曲线。

2 喷射器模型

2.1 喷射器结构模型

本文所使用的喷射器通过Taslimi[9]所提出的一维程序确定基础尺寸，并参考Zhu[10]、Liu[11]的方法进行优化，最后加入探针，得到可调喷射器方案。在喷射器的模型设计中，引入了如下假设：

a.不考虑喷射器的壁面厚度及内部可能的圆角。

b.根据Colarossi[12]的计算流体力学（Computational Fluid Dynamics，CFD）研究，使用二维轴对称模型来简化喷射器。

利用商业软件包ANSYS 中的绘图模块绘制喷射器二维模型，之后导入网格绘制工具中绘制结构化网格。喷射器二维模型如图1 所示，重要几何参数如表1 所示。喷射器结构简单，其主要原理在于高压的一次流进入缩放喷嘴后增速至超音速从而降低压力，受到压差的驱动，二次流体被引射进入预混合室，两者在预混合室中初步混合，并在等面积混合室中进一步混合，最后在扩压室中增压喷出。

表1 喷射器参数mm

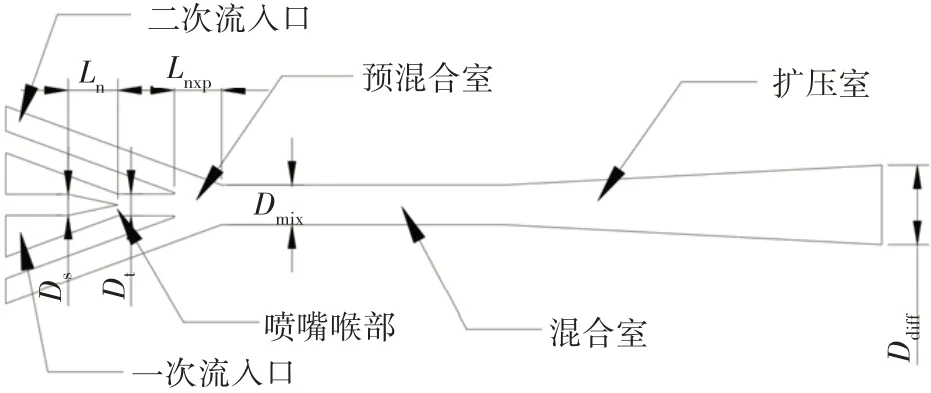
图1 喷射器模型

绘制的网格如图2 所示。值得注意的是，流动处于湍流状态，壁面处流动变化较大，因此在壁面处对网格进行了加密，绘制了边界层网格，如图3所示。同时，一次流动力喷嘴内部存在速度、压力的较大梯度，且伴随一定相变，因此在该处加密网格，提高计算的精度。

图2 喷射器网格

图3 边界层网格

为了在获取较为准确结果的同时保证较快的计算速度，进行了网格无关性分析，具体结果如图4 所示。由图4 中可知，网格数量在80 000 个左右时，不仅能够加快仿真收敛速度，结果也更加准确。

图4 网格无关性分析结果

2.2 CFD模型

在提出本文所使用的控制方程前，需进行以下假设：

a.喷射器壁面是绝热的，即内部流体不对外界传热，没有热损失。

b.忽略重力对流动的影响。

c.流动处于稳态，即输运方程中非稳态项不起作用。

根据连续性方程、动量守恒定律、能量守恒定律，具体控制方程为：

式中，i=x,y,z；j=x,y,z；ρ为密度；ui为笛卡尔坐标系下所在的坐标系平面i的速度分量；p为压强；τij为笛卡尔坐标系下切应力所在面的法线方向为i、切应力的方向为j的湍流应力；keff为有效导热系数；E=h-p/ρ+u2/2为流体微团的总能；h为焓值；T为温度；τeff为热源项。

本文使用的模型为HEM，其主要特点在于将流体视为始终保持热平衡和力平衡的状态，将具体的物性视为压力和焓的双值函数，通过确定每一点处流体的压力和焓确定该点处流体的物性参数，故需建立焓的输运方程。

通过ANSYS Fluent 中的用户自定义标量（User Defined Scalar，UDS）接口，用户可以自定义标量输运方程，焓输运方程[6]为：

式中，、分别为速度分量、焓值的费耶（Favre）平均量；1、2、3为源项，分别描述了机械能、动能变化的不可逆耗散、湍动能的耗散；Γh,eff为扩散系数：

式中，u、v、w表示为直角坐标下的速度分量；pˉ为压力的雷诺平均量；μ、μT分别为层流和湍流动力粘度；k为热导率；K为湍流动能；σT为普朗克数。

通过求解该焓方程，可以确定每一点处的焓，然后可以通过开源的COOLProp 软件[13]查得该点的密度、粘度、传热系数等参数，从而确定CO2的物性。值得注意的是，为了获取可信的马赫数，两相区声速的确定方法有所不同。声速的确定方法按照Cardemil[14]所使用的模型来计算：

式中，a为流体对应的声速；av、al分别为两相区对应的压力和温度下饱和蒸汽、饱和液体的声速；ϵv、ϵl分别代指气相和液相的孔隙率；aw为仅考虑压力平衡时的声速；ρv、ρl分别为液相和气相的密度；ζv、ζl分别为气相和液相的绝热节流系数；Cp,v、Cp,l分别为气相和液相的体积热容，且有：

式中，o=v,l；sv、sl分别为气相和液相的绝热过程；vv、vl分别为气相和液相的比容；cp,v、cp,l分别为气相和液相的定压比热容；βv、βl分别为气相和液相的热膨胀系数。

3 CFD仿真

本文使用商用软件Ansys Fluent 2020R2 进行CFD 仿真。计算中涉及焓，故需打开内置的能量方程。在湍流模型的选取上，与Lucas[8]和Liu[11]相同，本文采用能够更好地预测流动的局部及全局参数的剪切应力输运（Shear Stress Transfer，SST）k-ω模型[15]。在计算方法上使用了耦合算法，在收敛判据上将连续方程的残差设置为10-5，能量方程的残差设置为10-7，以确保计算达到收敛。

在喷射器性能考察方面，本文主要采用引射比Re，它体现了一次流引射二次流的强度，具体定义为：

式中，m、s分别为喷射器的一次流、二次流流量。

同时，根据Zhu[16]提出的喷射器效率计算公式，相同工况条件下，引射比越大，喷射器的效率越高：

式中，h7s为假设喷射器二次流进口等熵增压到出口压力时的焓；h7为二次流进口处的焓；h2为喷射器一次流进口处的焓；h2s为假设喷射器一次流进口等熵膨胀到出口压力时的焓。

3.1 HEM验证

为验证HEM 的准确性，本文选取文献[16]试验数据中的9个工况进行对比，具体工况如表2所示。

HEM 的仿真结果、文献[16]的试验数据及相对误差如图5、图6所示。

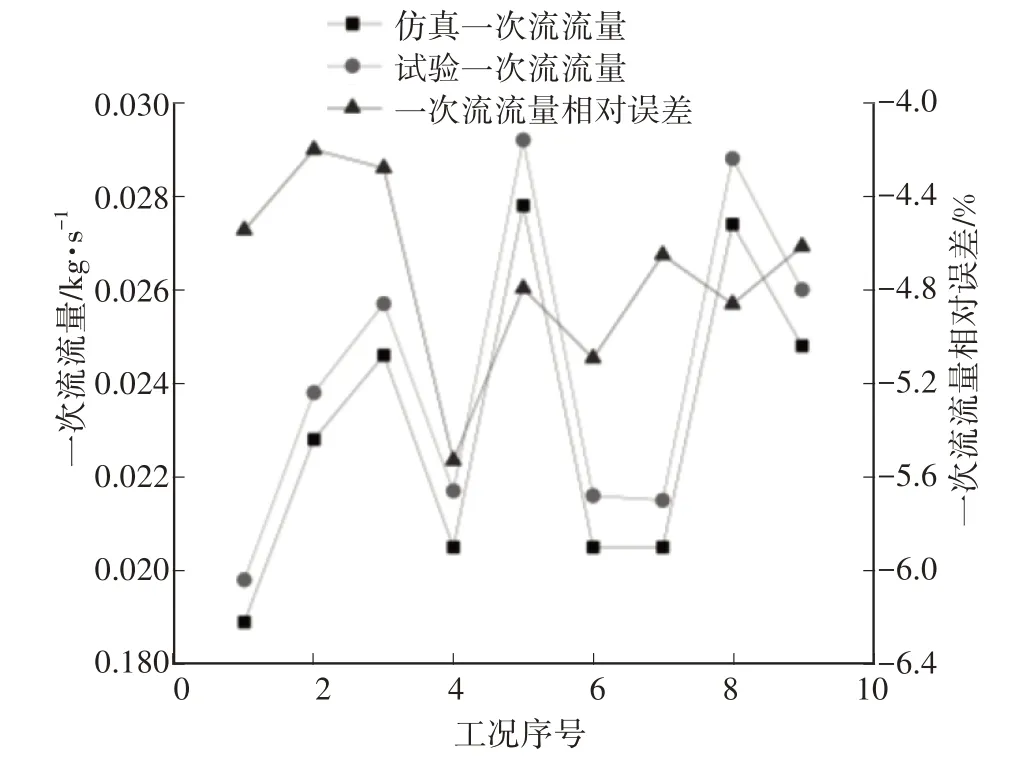
图5 一次流流量与文献[16]结果的对比情况

图6 二次流流量与文献[16]结果的对比情况

对比的9 个工况中，HEM 的一次流流量平均误差为4.73%，二次流流量平均误差为4.13%，误差均小于5%，说明HEM 能够正确反映喷射器的引射情况，可用于研究可调喷射器的性能。

3.2 不同探针型线的性能分析

本文设计了3 种型线的探针方案，分别为直线型、下凹型和上凸型，并研究了3种方案对可调喷射器性能的影响。目前常用的探针型线为直线，这种探针的特点在于在探针的不同部位有着相同的斜率，下凹型和上凸型型线探针的斜率在整个调节过程中始终发生变化，如图7所示。3种型线的探针具有相同的移动距离和最大半径，不同之处在于，用于调节喉部面积的区域的型线有所不同：直线型的型线是连接最大半径点和探针尖端点形成的；下凹型的型线是由通过最大半径点、通过探针尖端点及与对称轴相切于探针尖端点这3 个约束所形成的；上凸型的型线由下凹型的型线通过直线型的型线对称得到。

图7 探针的3种型线

为了获得相同的喉部截面积，以喉部处探针所占据的截面半径为标尺，沿着水平方向从探针尖端点的0 mm 到探针最大半径点的0.6 mm，设置了如表3所示的15个探针位置。

表3 探针位置设置

工况设置如下：一次流入口采用压力入口边界条件，压力为8.82 MPa，入口温度为308.15 K；二次流入口也采用压力入口边界条件，入口为压力3.30 MPa 的饱和气态CO2；出口使用压力出口边界条件，升压为0.67 MPa。

不同喉部处探针半径和截面积条件下，3 种探针方案的一次流流量、二次流流量及引射比如图8～图10所示。

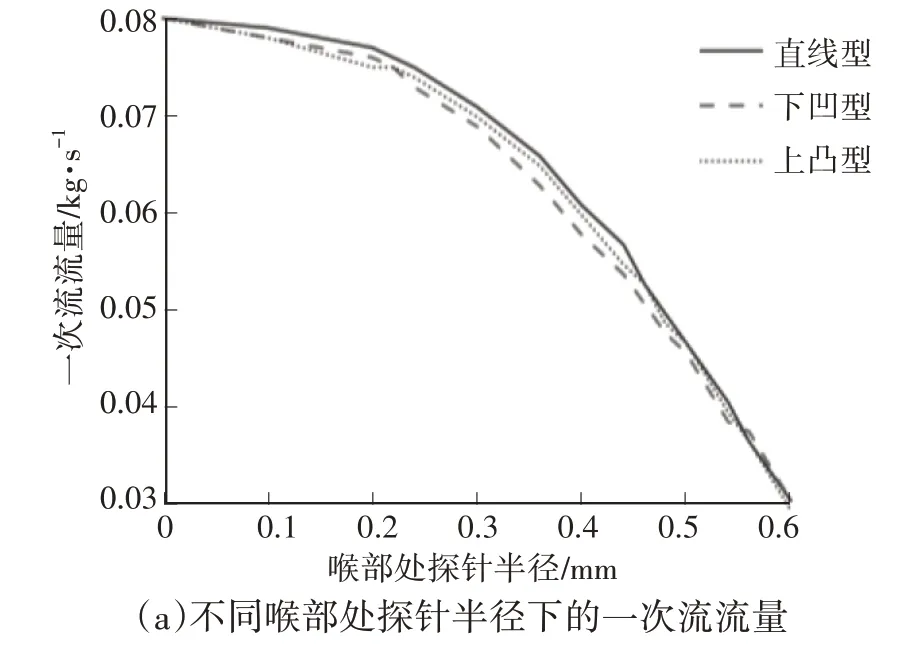
图8 不同喉部处探针半径和截面积下各型线探针方案一次流流量

图9 不同喉部处探针半径和截面积下各型线探针方案二次流流量

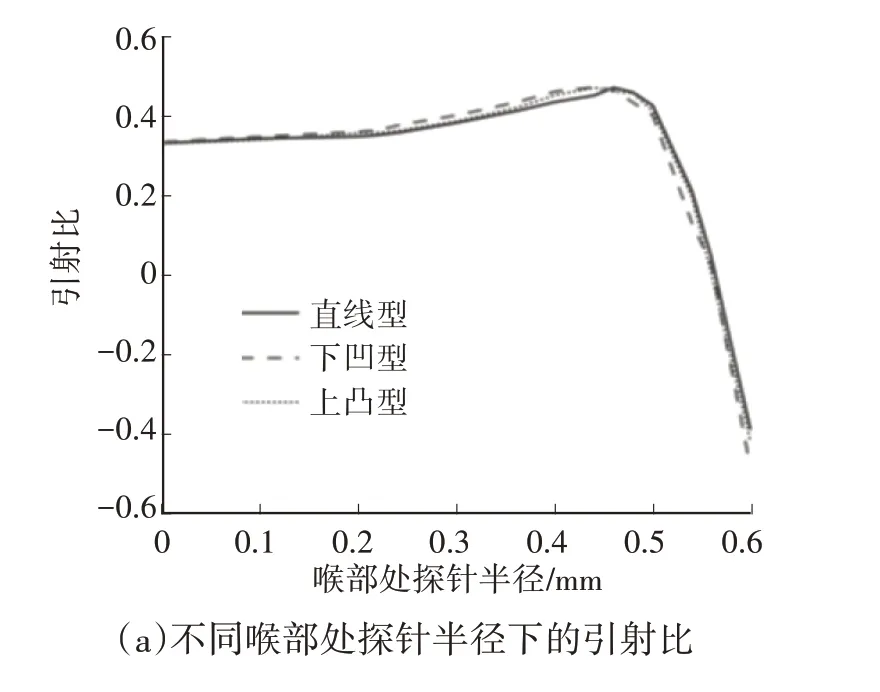
图10 不同喉部处探针半径和截面积下各型线探针方案引射比

对于3种型线探针的喷射器，一次流流量的下降趋势相同，即均随着喉部截面积的减小而线性减小。在喉部处探针半径较小时，3种型线的二次流流量几乎维持不变，而一次流流量下降，导致引射比随着喉部处探针半径的增大缓慢增大。当喉部处探针半径超过某一数值时，一次流在喷嘴出口处由欠膨胀向过膨胀发生转变，对二次流的引射能力降低，导致二次流流量大幅度下降，引射比也迅速下降。

分析引射比曲线可知，当喉部处探针半径为0～0.50 mm 时，喷射器的引射比处于较高水平。其中，在喉部处探针半径为0～0.44 mm 时，引射比始终处于增大趋势。这里将0.44 mm 称为高效调节半径，将0～0.44 mm 区间称为高效工作区。当喉部处探针半径超过0.50 mm时，引射比急剧下降，直至小于0，喷射器完全无法引射流体。因此，无论何种类型的探针，其调节范围均有限，应保持探针在高效工作区内移动，从而实现调节一次流流量的功能并保持喷射器性能处于最佳范围。

以直线型型线为基准，绘制了在喉部处探针半径为0～0.50 mm 范围内下凹型和上凸型2 种型线探针方案下一次流流量、二次流流量和引射比的相对偏差，如图11所示。

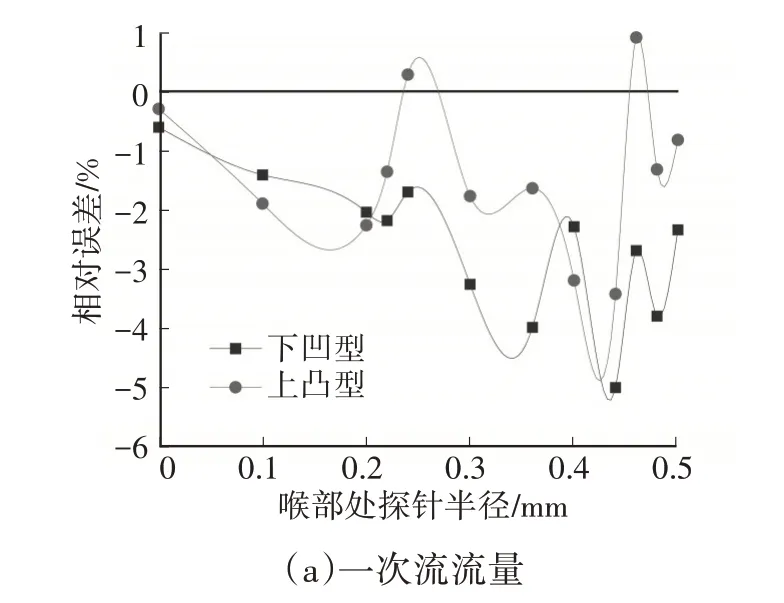
图11 下凹型和上凸型型线一次流流量、二次流流量、引射比的相对偏差

从图11a 中可以看出，在高效工作区内，直线型、上凸型、下凹型型线探针喷射器的一次流流量分别处于较高水平、中等水平和较低水平，最大相对偏差约为6%。这表明，即使喉部截面积相同，3种型线探针喷射器的一次流流量也会有所不同。

分析图11b 可以得出，在高效工作区内，3 种型线探针喷射器的二次流流量偏差最大值小于2%，其中下凹型型线探针喷射器的二次流流量始终处于较高水平，上凸型型线和直线型型线探针喷射器的二次流流量较为接近。

从图11c 中可以看出，在高效工作区内，下凹型型线探针喷射器的引射比总体高于其他2种型线探针喷射器引射比，上凸型型线探针喷射器的引射比略高于直线型型线探针喷射器的引射比。

喉部处探针半径为0.40 mm 时，喷嘴出口及预混合室内的压力分布云图如图12所示，轴线上压力分布对比如图13所示。

图12 喉部处探针半径为0.40 mm时3种型线探针喷射器的压力分布云图

图13 喉部处探针半径为0.40 mm 时轴线上压力分布情况

图12b的上凸型型线的探针尖端处存在较小的高压区，导致一次流受阻，使一次流流量较低。结合压力分布云图，在动力喷嘴出口处，即x=12 mm附近时，直线型型线探针喷射器的压力高于上凸型型线和下凹型型线探针喷射器的压力，因此引射能力更差，在一次流流量更大的情况下，无法比其他2种型线引射更多的流体。

上述分析都是建立在相同的喉部截面积条件下。图14 分析了一次流流量相同条件下3 种型线探针喷射器引射比的对比情况。从图14 中分析可得，一次流流量相同时，下凹型型线探针喷射器仍保持了较高的引射比，具备更高的喷射器效率。

图14 一次流流量相同时3种型线探针喷射器的引射比

在喷射器的高效工作区内，喉部截面积相同时，下凹型型线探针喷射器能够获得中等水平的一次流流量和较高水平的二次流流量，从而得到较高水平的引射比。在流动方面，下凹型型线探针喷射器不会在探针尖端处形成高压区，从而避免较大的压力损失，同时可在喷嘴出口处取得较小的压力，形成较大的压力差。相较于另外2 种探针型线，下凹型型线具有更佳的性能，在相同工况下能够获得最高的喷射器效率。

3.3 高效可调半径的分析

由3.2 节可知，针对出口背压为3.97 MPa 的工况，喷射器高效可调半径为0.44 mm。为分析高效可调半径与喷射器出口背压的关系，以上凸型型线探针喷射器为例，改变喷射器的出口背压，观测喉部处探针半径在0.36～0.46 mm 范围内引射比的变化情况。出口背压分别设置为3.87 MPa、3.97 MPa、4.07 MPa、4.17 MPa，一次流参数和二次流参数保持不变，一次流流量和引射比结果分别如表4 和图15所示。

表4 不同出口背压下各喉部处探针半径对应的一次流流量

图15 不同背压下引射比随喉部处探针半径变化情况

喉部处探针半径不变时，喷射器一次流流量不随出口背压的变化而变化，但是不同的出口背压对应不同的高效可调半径。随着出口背压的增大，高效可调半径不断减小，说明该可调喷射器的高效工作区的范围不断减小，喷射器调节一次流流量的能力下降。因此，对于已经确定尺寸的可调喷射器而言，升压越大，探针可移动的范围越窄，喷射器能够正常负载的一次流范围越小。表5列出了出口背压与高效可调半径之间的对应关系。

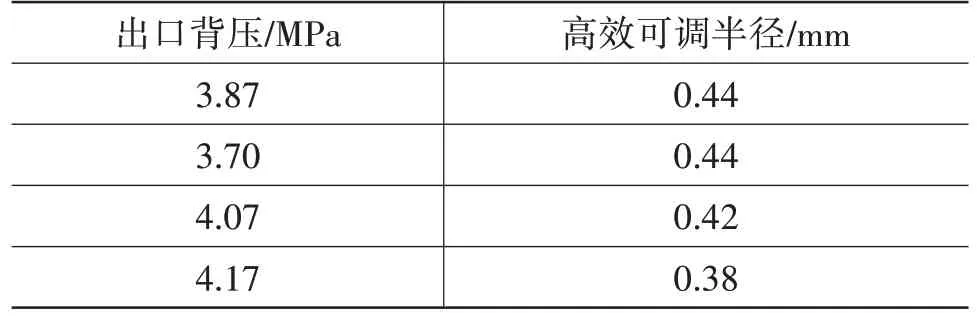
表5 不同出口背压对应的高效可调半径

4 系统分析

跨临界CO2汽车空调喷射器制冷循环的系统如图16所示。汽车空调所需的冷量在蒸发器处由CO2蒸发吸热获取。在保持蒸发器内蒸发温度和压力不变（即喷射器二次流进口温度和压力不变）的情况下，二次流流量越大，制冷量越大。同时，在保证一次流压力、温度及喷射器出口背压不变的情况下，一次流流量越小，压缩机做功越少。因此，在该系统中加入前文设计的可调喷射器后，其他参数不变时，喷射器引射比越高，系统的COP越大。

图16 跨临界CO2汽车空调喷射器制冷循环系统示意

对于本文提出的3 种型线，下凹型型线探针喷射器在整个一次流流量范围内引射比均处于较高水平，从而使系统的COP 也处于较高水平。使用下凹型型线探针的可调喷射器能够有效提高跨临界CO2汽车空调喷射器制冷循环的运行效率。

5 结束语

本文从可调喷射器的探针型线着手，设计了直线型、下凹型和上凸型3种型线探针方案，提出了高效可调半径的概念，并利用经验证的HEM 开展CFD仿真，分析了出口背压对高效可调半径的影响。最后，从系统的角度分析了喷射器性能与制冷系数的关系。主要结论如下：

a. 当探针轴向位置沿着流动方向移动时，3 种型线探针喷射器的一次流流量、二次流流量和引射比具有相同的变化趋势，引射比均先缓慢升高，超过高效可调半径后急剧下降。在相同使用条件下，采用下凹型型线探针的可调喷射器有着较高的效率和性能。

b.当出口背压发生变化时，可调喷射器对应的一次流流量不变，但高效调节半径发生了改变，两者呈负相关关系。因此，当系统需要较高的升压比时，喷射器能够负载的一次流流量下降，探针正常调节的范围缩小，导致制造能够同时广范围调节一次流流量和升压的可调喷射器的难度大幅提高。

c. 对于跨临界CO2汽车空调喷射器制冷循环，在相同工况下运行时，喷射器的引射比越高，系统的制冷系数越大。对于本文提出的3种型线探针喷射器方案，引射比处于较高水平的下凹型型线探针喷射器更具优越性。