基于IOWGA算子的生态足迹组合预测模型研究
陈兆言 CHEN Zhao-yan;张康静 ZHANG Kang-jing
(安徽财经大学统计与应用数学学院,蚌埠 233030)
0 引言
随着人类生产活动愈发活跃、科学技术不断发展,我国经济水平持续稳步前进,位居世界前列。但在有限的自然资源及生存空间下,人口的快速增长为生态环境和生物资源造成了空前的影响。William E Rees(1992)最早提出生态足迹作为衡量自然资源可持续性的定量指标,以其理论丰富的内涵与可操作性而受到广泛关注和推广。徐中民等率先将生态足迹理论引进国内,在此之后生态足迹及相关议题逐渐进入国内学者的视野,成为衡量自然生态状况的重要指标之一。生态足迹模型能够通过衡量人类与生态系统之间相互供给的产品与服务的差距,从而评估该区域的生态是否处于可持续发展状况。因此,对生态足迹进行相关预测研究,有利于对自然资源进行合理利用,减少污染情况,改善生态环境,实现可持续发展与绿色建设。
本文基于2003年至2014年①安徽省资源消费量计算人均生态足迹,并采用灰色GM模型、长短期记忆神经网络模型、差分自回归移动平均模型作为单项模型构建基于诱导有序几何加权平均算子(IOWGA)的组合预测模型,并将组合模型与单项模型进行预测效果比较。
1 理论基础
1.1 生态足迹模型及其计算
1.1.1 生态足迹模型
生态足迹(Ecological footprint,EF)也称为生物占用,是指具有生物生产力的地域空间,即要维持个体、地区或国家的生存所需、能够容纳人类所排放的废物的地域面积。生态足迹模型可以分为以下几个方面:①将人类消费资源进行分类;②将资源生产用地转换为用地面积;③将各用地面积加总即为生态足迹。
1.1.2 生态足迹计算
生态足迹主要可分为生物资源账户与能源账户。生物资源账户生态足迹可表示为:
其中,fi表示第i种生物资源的生态足迹;Ci表示第i种生物资源的年消费量;Yi表示生物资源的全球平均产量;Pi表示生物资源的年生产量;Ii、Ei分别表示生物资源的年进口量与年出口量。
假设进出口均衡,则人均生态足迹可表示为:
其中,EF表示总体生态足迹;N表示总人口数量;fi表示第i种生物资源或能源的生态足迹;rj表示各生物资源或能源对应的生产用地类型的均衡因子。
根据安徽省历年统计年鉴中记录的主要生物资源及能源的年消费量,结合全球平均产量、平均能源足迹及折算系数计算各资源的生态足迹,加总求得2003年至2014年安徽省的生态足迹数据,如表1所示。其中,式(2)所用到的均衡因子,采用以往文献研究中测算的结果。

表1 2003年至2014年安徽省人均生态足迹单位:hm2/人
1.2 单项预测模型
1.2.1 灰色GM(1,1)模型
灰色预测是同时包含已知信息与不确定信息的系统进行预测的方法,它对原始序列进行处理来寻找系统变化的规律,并生成有较强规律性的序列,建立微分方程模型。灰色预测特点是对数据需求量较小,预测精度较高。
灰色模型可表示为:
1.2.2 长短期记忆神经网络模型
LSTM神经网络是具有记忆长短期信息能力的神经网络。LSTM在RNN基础上,为了解决长期依赖性问题而进行了优化,在原有链式结构记忆单元上,通过时间反向传播算法对数据进行训练。
1.2.3 差分自回归移动平均模型
差分自回归移动平均模型在ARMA的基础上,对原始数据进行差分处理得到平稳序列,将预测对象随时间变化的序列视为随机序列,用一定数学模型近似地描述该序列。
1.3 IOWGA组合预测模型
IOWGA组合模型在传统加权算子赋权的基础上,较于传统算子模型改进了赋权灵活性,提高了预测精度。对于安徽省人均生态足迹的预测问题,设x1、x2、x3分别为灰色预测模型、LSTM模型以及ARIMA模型t时刻的预测值,设l1、l2、l3分别为各单项模型的权重系数。则t时刻各单项预测精度为:
预测精度与预测值构成了三个三维数组<p1t,x1t>、<p2t,x2t>、<p3t,x3t>。将三种单项方法在t时刻的预测精度按大小排序,设p-index(it)表示按上述规则排序后t时刻第i个预测精度的下标,则第t时刻的IOWGA组合预测值为:
组合预测的对数误差平方和S为:
其中,E为组合预测对数误差信息方阵,L=(l1,l2,l3)T。
对以下最优化问题进行求解即可得到组合预测权重系数l1、l2、l3:minS=LTEL
2 基于IOWGA模型的组合预测与分析
根据各账户测算的2003年至2014年安徽省人均生态足迹,分别采用GM(1,1)模型、LSTM神经网络模型以及ARIMA模型对数据模型进行构建,同时以IOWGA为基础,确定组合预测模型中各单项模型的权重,并构建组合模型,对安徽省人均生态足迹进行拟合与预测。
2.1 灰色GM(1,1)模型的预测分析
通过Matlab进行模型构建,可以得到GM(1,1)模型如下:
由模型计算预测值,如表2所示。

表2 安徽省人均生态足迹单项预测模型与组合预测模型拟合结果及预测精度比较
2.2 长短期记忆神经网络模型的预测分析
基于Python环境构建LSTM神经网络模型,进行生态足迹时间序列的一步预测。首先将2003年至2014年安徽省人均生态足迹的实际值进行标准化处理。将隐藏层节点设定为50,迭代1000次进行模型训练得到模型,输出预测结果,如表2所示。
2.3 ARIMA模型的预测分析
在2003年至2014年安徽省人均生态足迹的基础上,通过Eviews软件并采用ARIMA模型进行模型的构建。
2.3.1 平稳时间序列检验
首先对人均生态足迹原始数据进行单位根检验,结果显示单位根t统计量在1%、5%、10%显著性水平下均大于相应DW临界值,接受原假设,即人均生态足迹的原始序列为非平稳序列。因此,对原始数据进行对数化处理,并取一阶差分后再进行单位根检验。由单位根检验结果可知,对数化人均生态足迹的一阶差分在模型中引入截距项的情况下,其单位根检验的临界值在5%的显著性水平下均小于相应临界值,故可拒绝原假设,此时的对数化序列的一阶差分数据为平稳序列。
2.3.2 模型的建立及预测
对平稳序列进行自相关与偏自相关分析,自相关与偏自相关结果均表现出拖尾现象,故可建立ARIMA(p,d,q)模型。由上一节可得d=1,同时结合ACF与PACF结果可以大致判定ARIMA模型的范围。通过Eviews进行模型估计,确定最优模型为ARIMA(2,1,2),其中变量为AR(1)、AR(2)和MA(2)。
模型参数完成估计后,对模型的残差序列进行检验。结果显示残差序列不存在自相关情况,ARIMA模型表达式如下所示:
基于上述模型,对2003年至2014年人均生态足迹进行预测,预测结果如表2所示。
2.4 基于IOWGA算子的组合模型预测
设各单项预测模型所得的2003年至2014年安徽省人均生态足迹的预测值分别为f1t、f2t、f3t,预测精度分别为p1t、p2t、p3t。将各模型的预测值和预测精度代入式(5),得到基于IOWGA算子的组合预测值的表达式:
其中,l1、l2、l3为针对三种单项预测方法成分的权重。另外,可以得到最优化模型如下所示:
通过Matlab对最优化模型进行求解,得到IOWGA模型的最优权重系数l1、l2、l3,进而得到安徽省人均生态足迹组合模型的预测值,结果如表2所示。
3 模型的比较分析
通过上述各单项预测模型及基于IOWGA算子的组合预测模型获得相应预测结果,根据各模型的预测值绘制了预测结果的折线图进行直观对比,同时计算了5项拟合误差指标进行预测效果比较。
由于组合预测模型是基于IOWGA算子,将三种单项预测模型进行动态结合而成的,故IOWGA组合模型各年的预测值更接近实际值,预测精度最高。同时,对5种误差指标进行分析也不难看出,组合模型的拟合误差最小。这表明IOWGA组合模型的预测效果比任一单项模型效果都要更优,且预测结果与实际值趋势一致,更接近实际值,可以更好地对人均生态足迹进行预测,如图1所示。
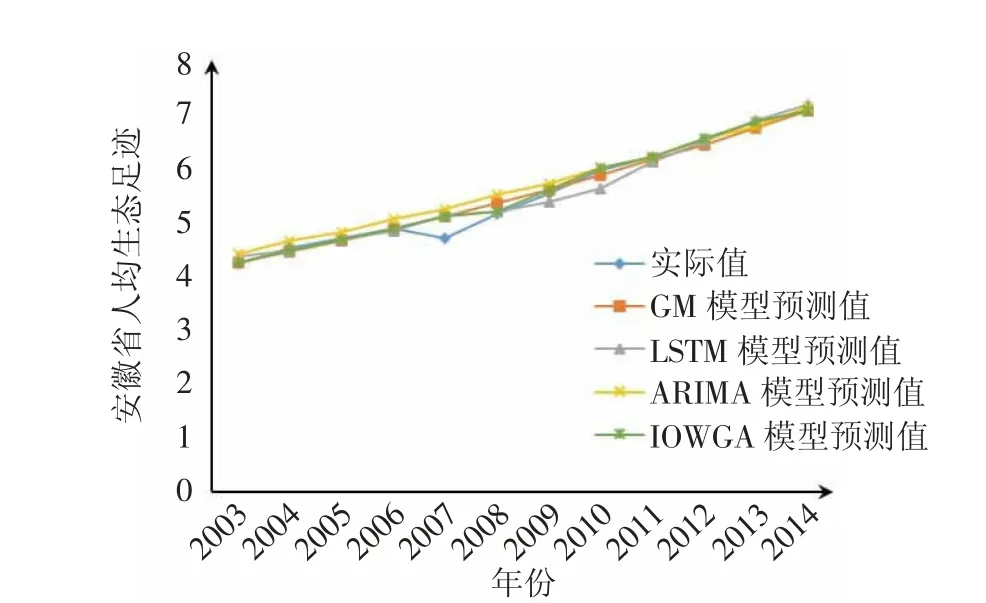
图1 各单项预测及IOWGA组合预测模型预测结果图
4 结论与建议
本文依据现有的相关数据,计算了安徽省2003年至2014年人均生态足迹,根据原始数据建立了灰色GM(1,1)模型、LSTM神经网络模型以及ARIMA模型,并基于IOWGA算子构建了组合预测模型。通过拟合误差指标的比较,可以得出基于IOWGA算子的组合预测模型可以有效提高预测模型精度,为生态足迹趋势分析及预测提供更加可靠的数据支持。根据预测模型的结果,可以针对生态足迹的增长趋势,在安徽省推广资源节约型生产模式,通过技术创新和产业升级,减少资源的消耗和浪费,从而在保障经济增长的同时减轻生态压力。其次,更加广泛地应用生态足迹的核算结果,将生态足迹作为评估指标,衡量政策、项目和发展计划对环境的影响,有助于防止过度开发和不可持续的做法,确保各项决策符合生态平衡原则。另外,人均生态足迹预测结果的准确性依赖于原始数据的精确程度。由于各生物资源及能源产品相关数据的统计口径易受政策等因素影响,对生态足迹的测度造成一定干预,预测精度受到影响,从而导致结果不稳定。生态足迹的不断增长给安徽省的生态系统安全带来了巨大挑战,为此要结合实际环境变化情况不断优化该组合预测模型,从而更好地为资源合理分配与环境治理提供参考依据。

