自复位刚性滑板隔震支座力学性能研究及优化设计∗

杨云舟，赖正聪，王 晶

（1.昆明理工大学建筑工程学院，云南 昆明 650500； 2.云南省工程抗震技术研究中心，云南 昆明 650500）

0 引言

近年来地震频发，隔震技术愈发受到人们关注，该技术使结构在地震中具备较高的安全储备，既可保护生命安全，又可保证财产安全。 目前对于隔震支座和隔震技术的研究主要以橡胶支座为重心，但橡胶支座存在橡胶老化、温度适应性差、耐久性低及污染环境等问题。 滑移摩擦隔震技术作为最早使用的隔震技术之一［1］，其基本原理是将隔震层设置为一个滑移层或滑动层，地震时上部结构通过滑移层相对于基础做水平滑移运动，实现基础与上部结构解耦，通过滑动摩擦耗散地震能量，减小传入上部结构的地震作用，降低上部结构的地震响应［2-5］。 而以摩擦滑移隔震技术为基础的滑板隔震支座无复位功能，在大震下常常会产生不可控的滑移，且震后会有较大残余位移，若增设限位装置则会增加成本，且构件与限位装置碰撞会使结构加速度产生扰动，影响隔震效能［6-7］。

针对上述问题，部分学者提出了组合隔震的概念。 由橡胶隔震支座与摩擦滑板隔震支座组成的组合隔震体系在工程中运用较为广泛［8-10］，该隔震体系兼顾了2 种支座的优点，避免了缺点。 李轩等［11］设计了一种以弹性滑板支座为主，辅以橡胶隔震支座及黏滞阻尼器的隔震系统，并验证了该组合隔震系统的有效性。 章征涛等［12］将组合隔震技术运用于某高层结构，取得了良好的隔震效果。 赵一敏［13］针对刚性滑板-复位橡胶新型组合式隔震支座设计了3 层钢框架结构模型作为上部结构，并进行振动台试验，证明了该组合隔震支座具备可靠的承载能力、水平恢复力和摩擦耗能能力。

本文基于组合隔震体系，对滑动摩擦元件与复位橡胶元件并联组成的自复位刚性滑板隔震支座进行研究，设置了不同竖向压应力、不同水平位移幅值及刚性滑块不同初始位置的试验工况进行压剪试验，探究试件在不同工况下的滞回特性。 针对该支座出现性能不稳定的问题，分析原因后对支座进行优化，对优化后支座进行压剪试验并运用有限元软件ABAQUS 进行数值模拟分析。

1 自复位刚性滑板隔震支座基本构造

自复位刚性滑板隔震支座基本构造如图1 所示。 其中：①上、下支座板均具有光滑的滑动镜面，刚性滑块均可在滑动镜面上滑动，即支座具备双滑动面，滑动镜面由不锈钢抛光打磨形成；②刚性滑块由球形板和中间座板组成，主材为钢材，是自复位刚性滑板隔震支座的主要承载构件，承担上部结构传递下来的全部竖向荷载，刚性滑块上、下面均镶嵌聚四氟乙烯（PTFE）板；③滑动镜面边缘布置4块限位块，可控制刚性滑块的极限位移；④支座边缘设置4 个复位橡胶块，复位橡胶不承担上部结构传递的竖向荷载，仅发生剪切变形。

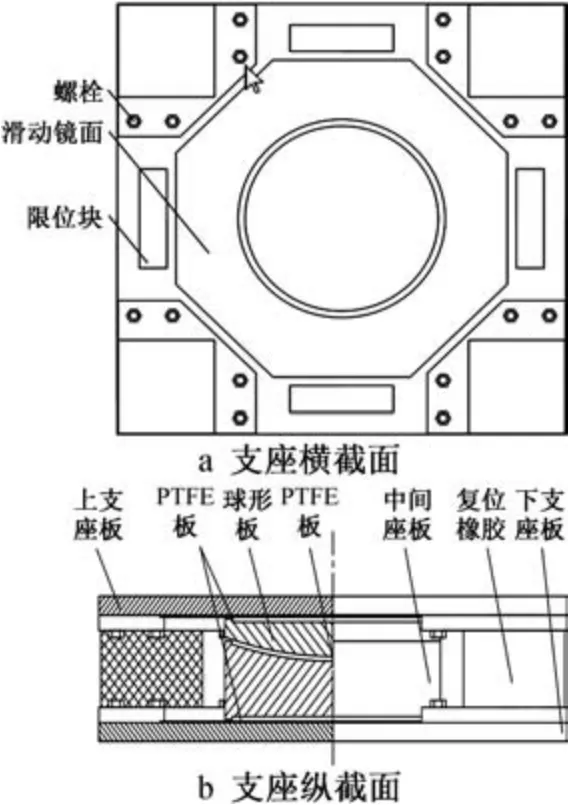
图1 自复位刚性滑板隔震支座Fig.1 Self-resetting rigid slide plate isolation support

自复位刚性滑板隔震支座将摩擦滑移元件与复位橡胶元件并联组成一种新型隔震支座，该支座同时具备滑动摩擦隔震技术与橡胶隔震技术的优点并有效避免了各自的缺点。 复位橡胶在地震作用下仅发生剪切变形，为隔震层提供一定的复位力，有效减小震后残余位移；刚性滑块依靠静摩擦力可以给隔震层提供一定的初始刚度，确保建筑在风荷载及地面激励较小时结构可正常使用，在遭遇较大水平荷载（水平荷载大于隔震层摩阻力之和）时使隔震层与上部结构解耦并通过摩擦消耗能量，消减上部的结构响应。

自复位刚性滑板隔震支座水平竖向双向解耦，各构件共同工作又相互独立，且具备复位、限位功能。 由于复位橡胶不承担上部结构传递的竖向荷载，在橡胶老化或损坏时无需更换整个支座，仅需拆卸螺栓即可更换橡胶元件，可不中断上部结构的使用功能。

2 自复位刚性滑板支座试验研究

2.1 试验加载装置

本试验在电液伺服压剪试验机（FJS1W5001）上进行（见图2）。 其额定垂直荷载为15 000kN，额定竖直行程为400mm，额定水平荷载为1 500kN，额定水平行程为520mm。 将自复位刚性滑板隔震支座和电液伺服压剪机连接，下盖板和支墩连接，上盖板由竖向油压千斤顶施加轴向力。 试验时垂直作动器先逐级加载至指定值，并在整个试验过程中保持不变，之后由水平作动器进行位移加载直至试验结束。

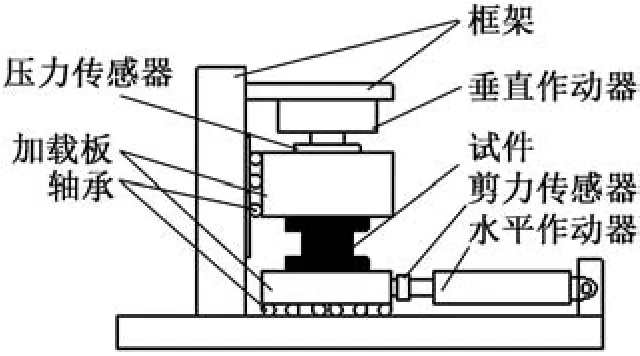
图2 加载装置Fig.2 The loading device

2.2 隔震支座试件

本次试验的自复位刚性滑板隔震支座如图3 所示，支座各部件尺寸如表1 所示。

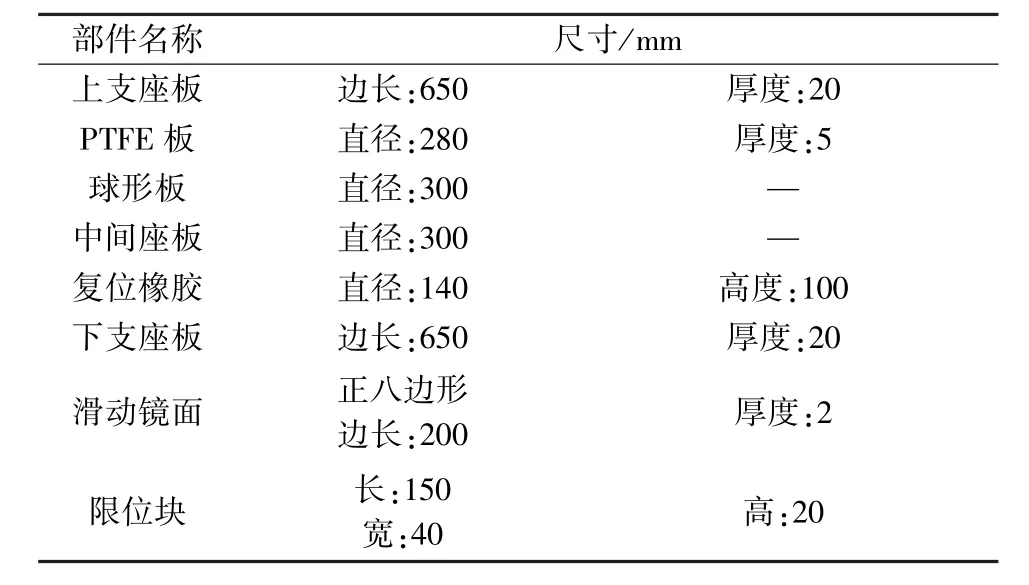
表1 支座各部件尺寸Table 1 Dimensions of each component of the support

2.3 不同竖向压力与水平位移对支座性能影响

为了研究竖向压力与水平位移对自复位刚性滑板隔震支座滞回性能的影响，试验设置竖向压力为20，30MPa，位移幅值为40，80，160mm 的试验工况。 根据试验所得的水平力-位移数据绘制支座整体在不同竖向压力下的滞回曲线。 图中取试验第3圈数据，如图4 所示。 由图可知，在水平位移一定时竖向荷载越大，滞回曲线越饱满。 原因是随着支座压应力增大，摩擦系数减小［14］，但减小幅度小于压力增大幅度，导致支座整体摩擦力增大，耗能效果增加，故滞回曲线更加饱满。 竖向荷载一定时，水平位移幅值越大，滞回曲线面积也随之增大，且当水平位移较大时，滞回曲线出现突变。

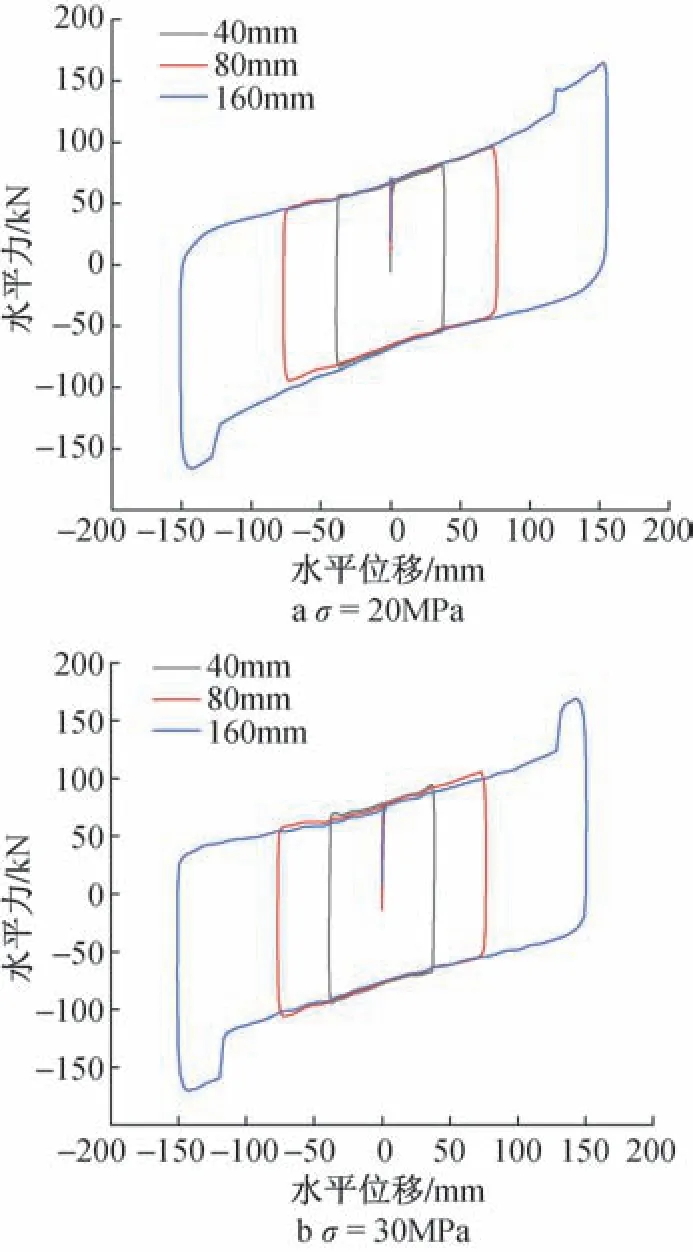
图4 不同竖向荷载支座整体滞回曲线Fig.4 Overall hysteresis curves of different vertical loads

2.4 刚性滑块不同初始位置对支座性能影响

自复位刚性滑板隔震支座在第1 次工作结束后，刚性滑块停留位置是随机的，下次工作开始时，刚性滑块从镜面上的随机位置开始滑动。 为了研究刚性滑块不同初始位置对支座整体性能的影响，本次试验设置了刚性滑块在30MPa 竖向压力下分别位于滑动镜面3 个不同初始位置的试验工况（见图5）。 根据试验所得数据绘制支座整体滞回曲线。取试验第3 圈数据，如图6 所示。 图中支座位移幅值为40，80，160mm，竖向压力为30MPa；当水平加载位移幅值为40mm 时，刚性滑块初始位置为位置1，滞回曲线并未出现任何突变。 当刚性滑块初始位置为位置2、位置3 时，滞回曲线均出现突变。 其原因是在水平加载位移幅值为40mm 时，初始位置为位置2、位置3 的刚性滑块在滑移一段距离之后与滑动镜面周边布置的限位块发生了1 次碰撞，因此滞回曲线发生突变。

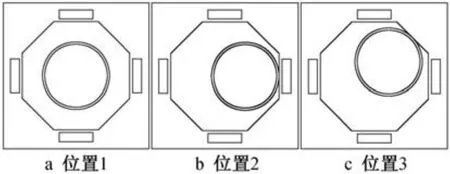
图5 刚性滑块初始位置Fig.5 Rigid slider initial position

当水平加载位移幅值为80mm 时，刚性滑块初始位置为位置1，滞回曲线并未出现任何突变。 当刚性滑块初始位置为位置2、位置3 时，滞回曲线出现突变，原因与上述原因一致。

当水平加载位移幅值为160mm 时，刚性滑块初始位置为位置1，2，3 时的滞回曲线均出现突变，其原因是：该支座设计时单面滑动位移极限设计值为100mm，该支座可双面滑动，支座整体的极限位移设计值为200mm。 因此当支座位移超过100mm 时，滑块滑动一个周期将会产生2 次碰撞，故滞回曲线发生2 次突变。

3 支座有限元模拟与分析

3.1 建模及参数定义

为了更接近试验时支座的受力分布和工作情况，以上述试验的试件为对象建立1 ∶1 等比模型进行数值模拟分析。 模型建立过程中复位橡胶采用超弹性本构Mooney-Rivlin 模型定义［15］，复位橡胶为超弹性体，且竖向荷载由刚性滑块承担，其不可压缩常数应为0，但考虑到有限元的计算过程及收敛情况，设置橡胶材料不可压缩常数D1＝0.001，橡胶剪切模量取G＝0.65MPa。 模型钢材选用Q235钢，钢材本构采用双曲线理想弹塑性模型，取弹性模量E＝210GPa，屈服后第2 阶段刚度系数取0.002，泊松比为0.3。 龚健等［16］提出将支座滑动摩擦的过程控制在弹性受力状态，能够较好地模拟滑动摩擦的过程。 所以根据聚四氟乙烯（PTFE）板的实测值，采用与钢材相同的各向同性弹性体本构模型来定义PTFE 材料，故弹性模量E＝280GPa，泊松比为0.42，设计强度为30N／mm2。 模型网格划分如图7 所示。

图7 支座有限元网格划分Fig.7 Bearing finite element meshing

3.2 试验结果与模拟结果对比

运用ABAQUS 对竖向压力为30MPa、水平位移加载幅值为40，80，160mm 的试验工况进行数值模拟分析。 数值模拟结果与试验结果对比如图8 所示。 由图可知：支座整体滞回曲线饱满，数值模拟结果与试验结果基本吻合，当位移幅值较大时试验结果与模拟结果均出现了滞回曲线突变的情况。通过ABAQUS 应力云图可以反映试验中难以观察的滑块碰撞情况及应力应变情况，如图9 所示。 据此可分析滞回曲线突变原因：在该支座中刚性滑块承担全部的竖向荷载，复位橡胶不承担竖向力，随着刚性滑块的滑动摩擦，当初始滑动面（下滑动面）碰撞到限位块时，刚性滑块上的应力分布发生了较大的改变。 从一开始应力较为均匀分布到应力向碰撞一侧集中增大，导致滑动摩擦接触面上应力增大，摩擦力也随之增大，从而导致滞回曲线发生突变。 分析其构造原因是该支座的刚性滑块由球形板与中间座板组成，碰撞之后球形板与中间座板产生微小滑动使应力重分布，引起滞回曲线突变。

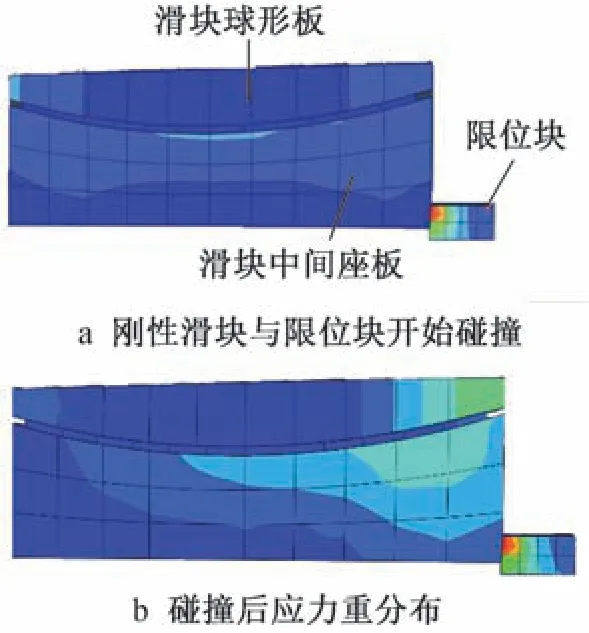
图9 有限元分析Fig.9 Finite element analysis

4 支座优化及试验研究

为了解决上述存在的问题，提高自复位刚性滑板隔震支座力学性能的稳定性，对支座进行优化。将刚性滑块优化为一个整体，复位橡胶分开布置为上下2 层；中间设置1 块复位板，该复位板能传递复位橡胶提供的复位力使刚性滑块向初始位置滑动复位，同时增加的复位板也可以控制刚性滑块的极限位移，不会让刚性滑块滑出设计的滑动镜面，取代限位块的作用。 刚性滑块将不产生任何碰撞，解决了过往研究中因为限位装置的碰撞而带来的各种难题，优化后支座的构造如图10 所示。

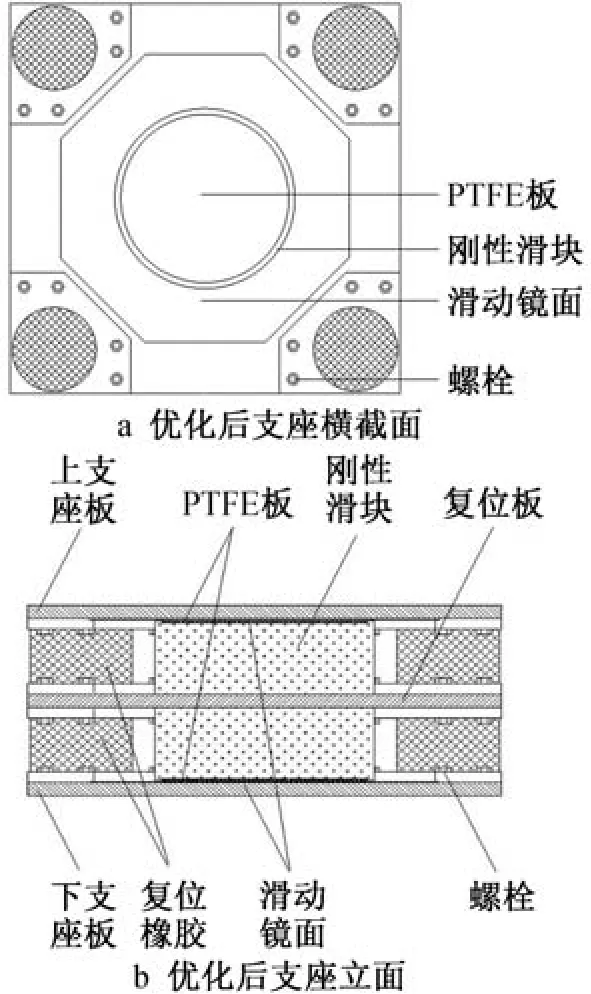
图10 优化后的自复位刚性滑板隔震支座构造Fig.10 Structure of self-resetting rigid slidingplate isolation support after optimization

由支座构造可知，优化后复位橡胶由原来的单层变为双层，即优化前单个复位橡胶的剪切刚度为：

整体复位橡胶提供刚度为：

而优化后单个复位橡胶的剪切刚度为：

优化后上、下2 层复位橡胶提供的刚度相等且单层复位橡胶的刚度为：

根据刚度串联公式［17］，优化后复位橡胶提供的总刚度为：

式中：G为剪切模量（MPa）；A为橡胶横截面积（mm2）；TR为橡胶厚度（mm）；Kq为优化前单个橡胶的剪切刚度（kN／mm）；KqT为橡胶的总剪切刚度（kN／mm）；Kh为优化后单个橡胶的剪切刚度（kN／mm）；K1hT为优化后单层橡胶的剪切刚度（kN／mm）；KhT为优化后橡胶的总剪切刚度（kN／mm）。

对比式（2），（5）可知，优化前后复位橡胶元件为支座提供的总刚度不变，即使用橡胶量相同的情况下，优化前后复位橡胶元件提供给支座整体的总刚度与复位力是一致的。 复位橡胶依旧不承受竖向荷载，仅发生剪切变形，为隔震层提供复位力和一定刚度。

优化后隔震支座的工作过程可分为以下几个阶段。

1）第1 阶段 该阶段工作原理与优化前的隔震支座一致，即自复位刚性滑板隔震支座依靠刚性滑块提供的静摩擦力而具备较大的初始刚度，当水平激励较小时（如强风或微小地震下），上部结构所受的剪力小于隔震层滑动摩擦的临界值（隔震层布置的支座最大静摩擦力之和），支座不滑动，此时自复位刚性滑板隔震结构动力响应与传统抗震结构一致。

2）第2 阶段 随着水平激励的增大，上部结构所受的剪力大于隔震层滑动摩擦的临界值。 支座开始滑动，发挥隔震效能，上部结构自振周期增大，偏离地震卓越周期，滑块通过滑动摩擦耗散地震能，减弱上部结构地震响应。 在滑动过程中，当刚性滑块的初始滑动面滑移到一定位移量，此时上、下2 层复位橡胶剪切变形量不一致，复位橡胶提供的复位力通过复位板传递到限位块的力也不一致，导致初始滑动面停止滑动，另一个滑动面开始滑动，滑移到一定位移量时，初始滑动面开始滑动，另一滑动面停止滑动，依次循环往复。 复位板依靠复位橡胶的复位力对刚性滑块实现了限位功能，完全摒弃需要通过碰撞来限位的方法。

3）第3 阶段 随着水平激励的停止，隔震层因复位橡胶剪切变形提供的复位力大于摩阻力，隔震层在复位力的作用下开始复位。 同时复位橡胶提供的复位力传递到复位板，复位板与刚性滑块同时向原位置复位。 每次工作结束后，刚性滑块的最终位置基本在原位置周围，下次滑块滑动时初始位置也与原初始位置基本一致。

为了验证自复位刚性滑板隔震支座优化后的相关性能，联系产家生产了一个优化后的自复位刚性滑板支座进行试验。 试验支座试件如图11 所示，支座各部件尺寸如表2 所示。

表2 试件各部件尺寸Table 2 Dimensions of each component of the specimen

图11 优化后的自复位刚性滑板隔震支座Fig.11 The optimized self-resetting rigid sliding plate isolation bearing

本次试验主要对优化前存在的问题及优化后的性能稳定性进行研究。 为了研究优化后自复位刚性滑板隔震支座否会出现优化前滞回曲线产生突变的状况，设置竖向应力为30MPa，水平位移加载幅值为50，100，150，200，250mm 5 种试验工况。 同时为了研究该支座耗能耐久性，设置竖向应力为30MPa，水平位移加载幅值为50mm，往复循环加载33 圈的试验工况。 设备信息与操作方式与上文试验一致。

根据试验所得数据绘制滞回曲线，如图12所示。

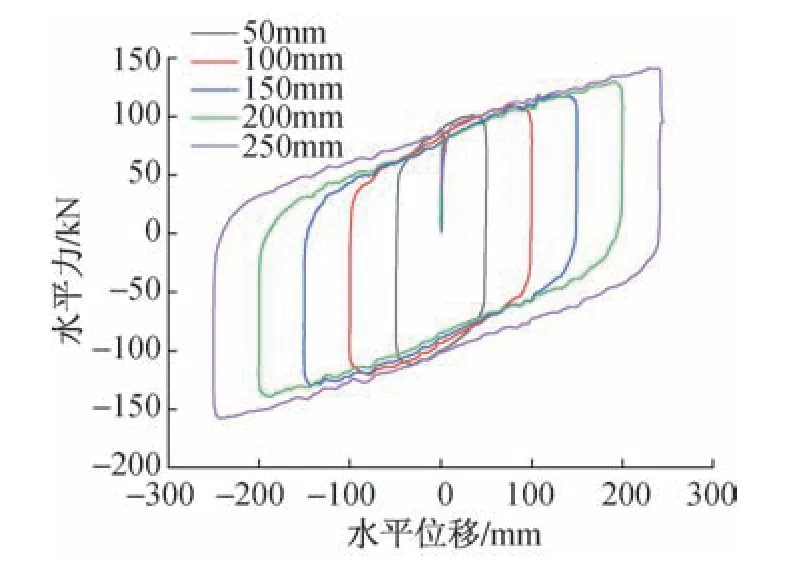
图12 支座优化后滞回曲线Fig.12 Hysteretic curve of optimized bearing

由图12 可知：竖向应力为30MPa，水平加载幅值为50，100，150，200，250mm 的试验工况下，支座的滞回曲线饱满，随着位移加载幅值增大，滞回环面积也增大，耗能能力也随之增大，不同位移幅值下滞回曲线稳定，未出现优化前支座滞回曲线突变情况。

5 优化后的支座有限元模拟与分析

以上述试验试件为数值模拟分析对象，同时为了更接近试验时支座的受力分布和工作情况，建立1 ∶1 等比模型进行数值模拟分析（见图13），材料参数定义与模拟过程与上文一致。

图13 优化后支座有限元网格划分Fig.13 Optimized bearing finite element meshing

优化后的隔震支座试验结果与模拟结果对比如图14 所示，优化后隔震支座试验结果与模拟结果基本吻合（曲线略波动是由于试验时电液伺服压剪机油压不稳定），且该支座在任何位移量上滞回曲线均无突变。 与优化前的支座相比，优化后隔震支座无需产生碰撞即可对刚性滑块完成限位，工作结束后滑块可复位，支座整体隔震效能更加稳定。

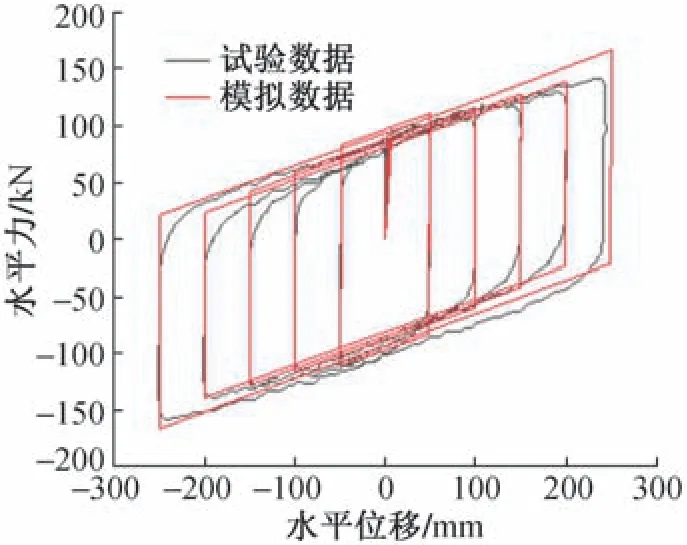
图14 优化后支座滞回曲线对比Fig.14 Comparison of the bearing hysteresis curves after optimization

6 结语

1）压剪试验下自复位刚性滑板隔震支座滞回曲线饱满，支座耗能与竖向压应力、水平位移幅值成正比，但水平位移幅值较大时支座滞回曲线出现突变。

2）支座刚性滑块与限位块碰撞时，滞回曲线出现突变，结合试验与有限元软件分析，原因是刚性滑块由球形板与中间座板组成，当刚性滑块滑动碰撞到限位块时，球形板与中间座板发生微小滑动，致使刚性滑块从应力均匀分布到应力向碰撞一侧集中增大，导致摩擦力也随之增大，从而使滞回曲线发生突变。

3） 对优化后的支座进行压剪试验并运用ABAQUS 进行数值模拟分析，试验与数值模拟结果一致，表明优化后的支座滞回曲线突变问题得以解决，消除了刚性滑块在滑移过程中因碰撞限位块引起的隔震效能不稳定状况，构造更加合理。