廊坊市大气能见度与相对湿度、PM2.5、PM10间的关系研究
张馨木 郭淑静 郭立平 张卫中




摘要 为研究大气能见度与相对湿度、气溶胶浓度之间的关系,选取2019—2021年逐年逐小时的廊坊市国家气象观测站能见度、相对湿度数据以及环保局PM2.5、PM10数据,将其之间的关系进行量化分析。结果表明:能见度与相对湿度、PM2.5、PM10浓度均呈显著负相关;不同季节,大气能见度与相对湿度的非线性相关性与线性相关性差别不大,相关系数均在0.7左右,冬季相关性略高;大气能见度与PM2.5的相关性均大于PM10;大气能见度与PM2.5、PM10浓度呈指数函数关系,与相对湿度呈3次方多项式关系,相关性均达0.6以上。利用相对湿度、PM2.5、PM10浓度分不同季节对大气能见度进行非线性拟合,并对结果进行检验,模拟能见度与实际能见度相关性达0.95,该拟合公式能较好地模拟能见度。
关键词 能见度;相对湿度;PM2.5;PM10;拟合
中图分类号:P427 文献标识码:B 文章编号:2095–3305(2023)09–0-04
作为了解大气的稳定性和垂直结构的重要天气指标之一,能见度是保障交通运输安全的一个极为重要的因素。以能见度表征大气透明度,不同的天气现象均会对大气能见度产生一定的影响。
20世纪,国外一些学者就研究发现了大气能见度和气溶胶间存在的相关关系[1-2]。此后,国内一些学者对大气污染物时空变化特征与气象条件的关系进行了研究[3-5]。大量研究表明,能见度与大气相对湿度及气溶胶颗粒物等气象因素都有一定的关系。如吕建华等[6]研究得出在各项大气污染物中,颗粒物对能见度的影响最大,且不同季节条件下,相关性存在一定的差异。王淑英等[7]、张凯等[8]对京津地区的观测数据进行研究,发现能见度与相对湿度在不同季节下呈现明显且规律不同的负相关。郝巨飞等[9]也发现相对湿度和PM2.5质量浓度与大气能见度有很好的负相关。张琳等[10]、宋明等[11]通过分析相对湿度、PM2.5、PM10质量浓度的关系,建立了多元大气能见度拟合公式,揭示颗粒物浓度和相对湿度对能见度的影响规律。
受大气能见度观测手段和观测密度的影响,国内相关研究多是以日数据为基础的,以分析得出月、季、年变化特征,且现阶段测量大气能见度大多是根据散射系数估算消光系数的,从而计算得到气象光学视程,缺乏检验和修正。因此,选取2019—2021年逐年逐小时的廊坊市国家气象观测站能见度、相对湿度数据及廊坊市环保局PM2.5、PM10数据,尝试用相对湿度、气溶胶质量浓度推算模拟大气能见度,为开展基于多源观测资料的能见度数据质量控制、校验和再分析及业务预报大气能见度提供参考。
1 资料来源与处理
地面观测资料来自廊坊国家观测站2019—2021年逐小时能见度、相对湿度数据,能见度仪量程0~30 km,数据质量高且具有连续性,按河北省地面气象观测业务技术规定进行定期人工订正质控,根据《地面气象自动观测规范》《新型自动气象站实用手册》对设备按时校准。颗粒物质量浓度数据来自环保局2019—2021年逐小时逐日PM2.5、PM10资料,获取数据后按3倍标准差法对数据进行预处理,并结合当日的天气状况剔除无效数据和异常数据。
2 结果与分析
2.1 能见度与各影响因子随时间变化规律
由图1可以看出,能见度、相对湿度、PM10、PM2.5的季节变化特征明显。廊坊市4、5月的能见度较高,5月达到峰值19.8 km,1—2月和7月的能见度较差;7—9月相对湿度较大,均达70%以上,其余月份值较低,4月最低,仅为40.9%(圖1a)。PM2.5、PM10的变化趋势高度相似(图1b),1—2月较高,4—9月处于低谷,峰值分别为2月的70.2 μg/m3(PM2.5)、1月的108.2 μg/m3(PM10),8月浓度最低,仅为25.7 μg/m3(PM2.5)、50.0 μg/m3(PM10)。这可能与廊坊的天气状况有关,廊坊春季多为大风天气,能见度良好,相对湿度较低,有利于污染物扩散;夏季多雨水,7—9月为廊坊主汛期,降水较多,相对湿度较大,降水对颗粒物具有一定的清除作用,导致PM2.5、PM10浓度相对较低;而冬季静稳天气偏多,气溶胶不易扩散,加之燃煤影响,使PM2.5、PM10浓度达到高值。
图2a为能见度与相对湿度的日变化曲线,可以看出其存在明显的日变化规律,相对湿度在06:00达全天最高值70.4%,后逐渐减小至15:00的39.0%为谷值,15:00后至夜间逐渐增大,能见度正与之相反,06:00能见度最低,后逐渐上升,16:00达峰值后下降,可以看出能见度与相对湿度存在明显的负相关关系。图2b为PM2.5与PM10的日变化曲线,PM2.5和PM10浓度日变化趋势基本一致,呈双峰型。在07:00~09:00浓度达峰值,此时为早高峰时期,车流量较大;随后气温升高,均在15:00达浓度最低,夜间21:00为次高峰,夜间浓度均偏高,与夜间大气层结状态较稳定、污染物不易扩散有关。
2.2 能见度与各影响因子线性相关性分析
不同湿度条件下,大气能见度及PM2.5、PM10浓度分析结果表明(表1),随着相对湿度的不断增加,能见度明显下降,可见相对湿度的增加是降低大气能见度的重要因素。当相对湿度在0%~69%,随着相对湿度的增加,PM2.5、PM10浓度均逐渐升高,能见度逐渐下降,可见PM2.5和PM10也对降低大气能见度有一定的贡献。但在相对湿度70%以上,随相对湿度的增加,PM2.5、PM10浓度变化出现了先减小后增加再减小的不稳定趋势,这可能是由于高相对湿度存在降水过程,而降水对颗粒物具有一定的吸附清除作用。
利用Excel表格分四季对数据进行线性拟合,相关系数见表2。可以看出,除夏季能见度与PM10浓度相关性较弱外,不同季节大气能见度与PM2.5、PM10浓度、相对湿度均存在0.5以上的强线性相关性。不同季节,大气能见度与相对湿度的相关性差别不大,相关系数均在0.7左右,冬季相关性略高,春季相关性略低。大气能见度与PM2.5浓度的相关性明显大于PM10,与PM2.5浓度春、冬季相关性较好,与PM10浓度冬季相关性最高,两者均在夏季的相关性最差,可能由于夏季降水的清除作用使污染物浓度下降,湿度较大,使夏季PM2.5、PM10浓度不足以作为影响能见度的主要因子,此时能见度主要受湿度影响。
2.3 大气能见度与PM2.5、PM10浓度的非线性关系
为进一步验证能见度与相对湿度、PM2.5、PM10浓度的关系,将相对湿度划分为9个等级,利用SPSS 16.0软件对其按下式进行指数拟合。
Vv=ae(bx)+c(1)
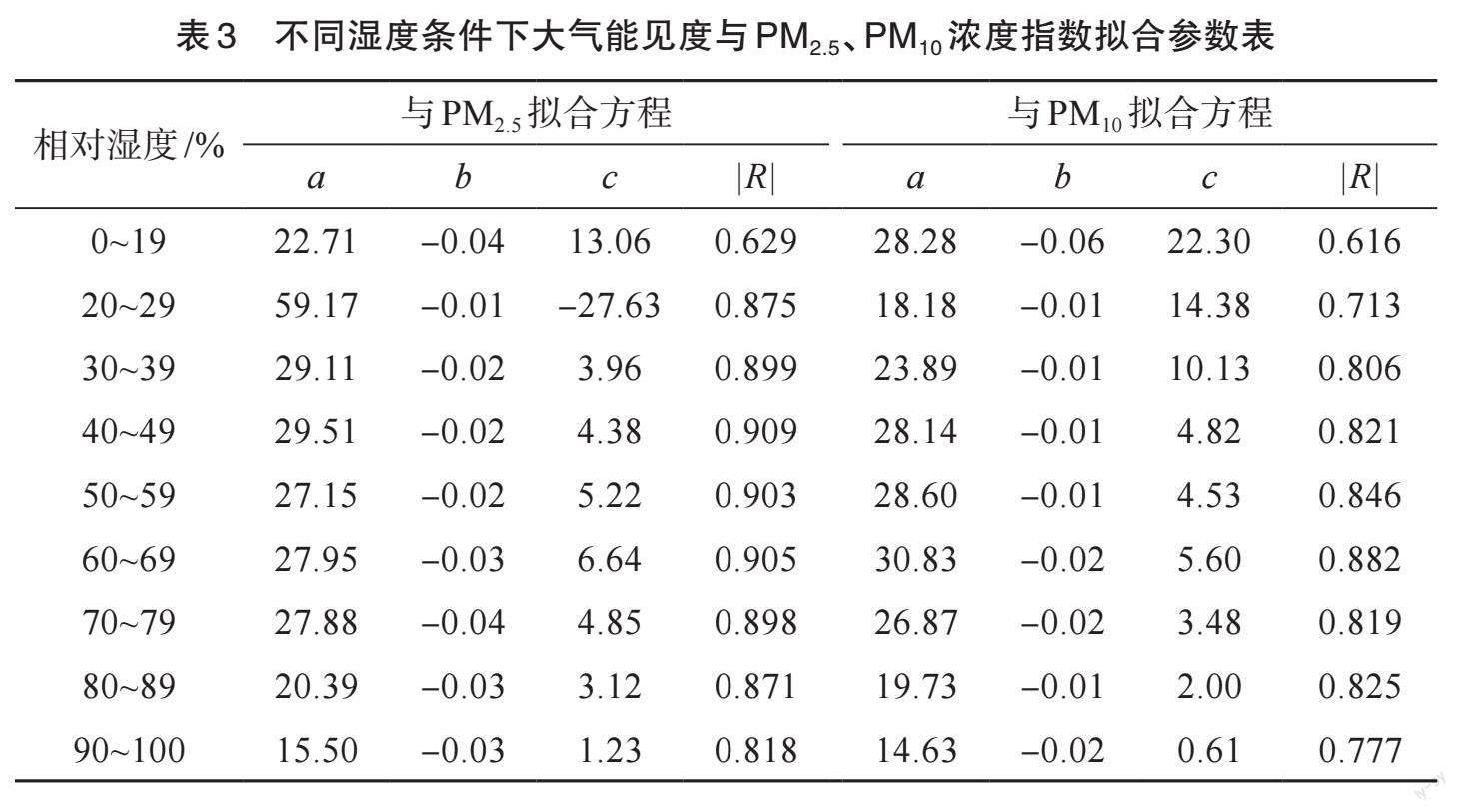
式(1)中Vv为能见度,x为PM2.5或PM10浓度,a、b、c为系数。表3为不同湿度条件下,大气能见度与PM2.5、PM10浓度的指数拟合参数表,表中可以明显看出,大气能见度与PM2.5、PM10浓度有着很强的指数相关性。当相对湿度在70%以下,随湿度的增加,大气能见度与PM2.5、PM10浓度的指数相关性逐渐升高,在相对湿度60%~69%,相关性最高。相对湿度大于70%时,随相对湿度增加,相关性开始有所下降,此时相对湿度较大,颗粒物吸湿,粒径增大,消光性增强,大气能见度主要受相对湿度的影响,受PM2.5、PM10浓度的影响相对会有所减弱。
2.4 大气能见度与相对湿度的非线性关系
为明确能见度与相对湿度的关系,使用SPSS 16.0软件对其进行多种非线性拟合发现,能见度与相对湿度的3次方多项式有较好的擬合关系,其拟合方程如下:
Vv=a+bx+cx2+dx3(2)
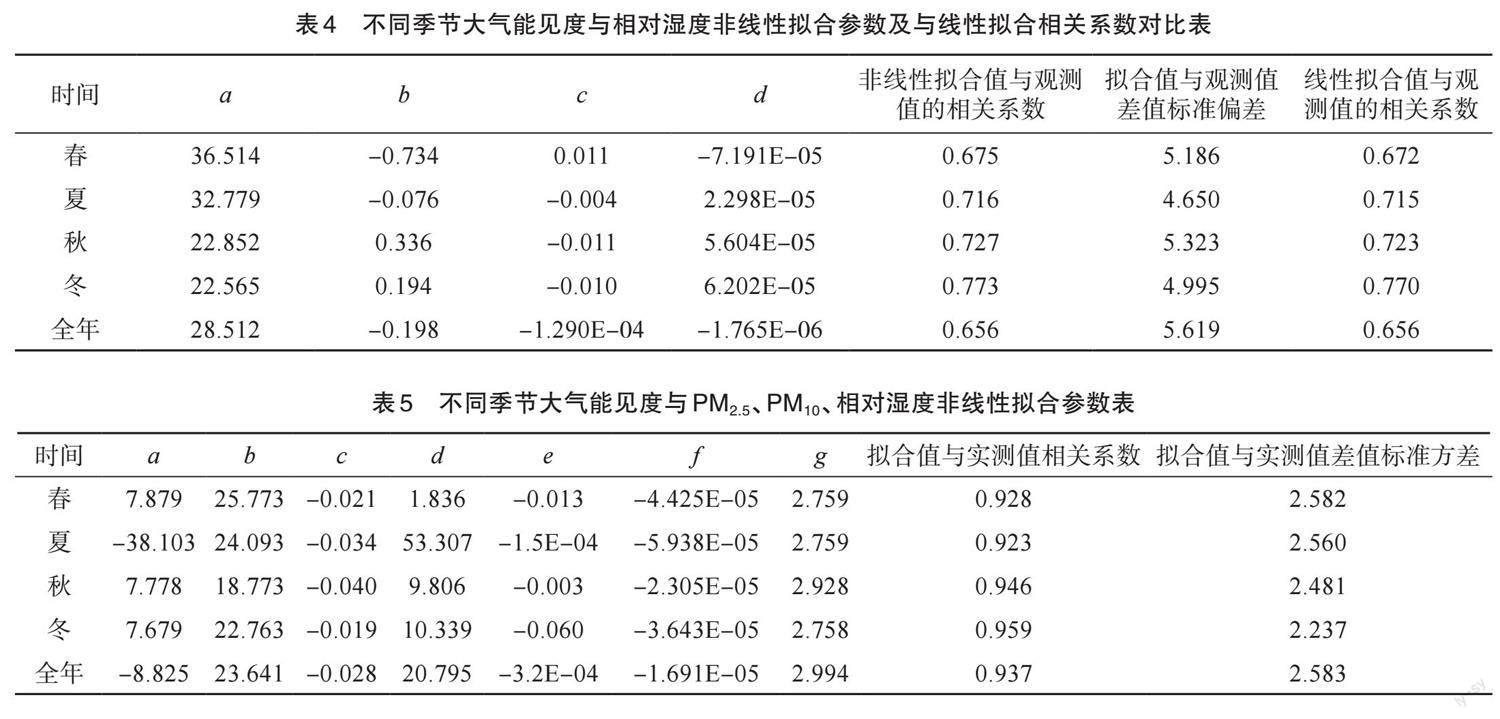
式(2)中,Vv为能见度,x为相对湿度,a、b、c为系数。表4为不同季节不同拟合公式的能见度与相对湿度的相关系数,并将其相关性与线性相关性进行对比。由表4可以看出,不同季节大气能见度与相对湿度的非线性相关性与线性相关性相差不大,说明公式(2)也能很好地模拟能见度和相对湿度之间的关系。大气能见度与相对湿度在冬季的相关性最高,春季最低。
2.5 大气能见度与各要素的多元非线性拟合公式
根据以上研究发现,大气能见度受相对湿度和PM2.5、PM10的浓度影响明显,利用SPSS 16.0软件多次迭代进行多元非线性拟合来模拟大气能见度。不同季节,大气能见度与PM2.5、PM10、相对湿度非线性拟合各参数见表5。Vv=a+b×ec×PM2.5+d×ee×PM10+f×RH g (3)
式(3)中,Vv为能见度(km),a、b、c、d、e、f、g为系数。由表5可以看出,不同季节,用相对湿度和PM2.5、PM10浓度模拟出的大气能见度值与实际测得的大气能见度值相关性均在0.92以上,说明该非线性方程能很好地模拟大气能见度。
2.6 大气能见度非线性拟合公式检验
为进一步检验模拟方程的准确度,将模拟得到的2022年1月的能见度小时值与2022年1月实际观测值进行对比,观测值和模拟值随时间的变化(图3),其中灰色柱形为观测值,黑色折线为模拟值,可以看出,模拟值与观测值随时间变化趋势大致吻合,但因能见度仪自身的量程限制,该模拟方程对能见度30 km以上和5 km以下的能见度的模拟效果较差。图4为模拟能见度与实测能见度的散点图,图中可以看出模拟值与实测值的相关性高达0.951,说明该方程能较好地模拟能见度,可以用式(3)通过相对湿度、PM2.5、PM10浓度模拟能见度。
3 结论
研究2019—2022年廊坊市大气能见度与相对湿度、PM2.5、PM10数据,分析大气能见度与相对湿度、PM2.5、PM10浓度间的关系,得出以下结论。
(1)大气能见度具有明显的季节变化特征,春季最高,冬季较低,夏季强降水时能见度最低。相对湿度7—9月最高,春季最低。PM2.5、PM10浓度冬季最高,7—9月最低。
(2)大气能见度、相对湿度、PM2.5、PM10均存在日变化规律。大气能见度与相对湿度呈负相关,PM2.5、PM10在早间(07:00~09:00)浓度最大,下午(15:00)浓度最低。
(3)大气能见度随相对湿度的增加而下降。当相对湿度在70%以下时,PM2.5、PM10浓度随相对湿度的增加而上升;当相对湿度大于70%时,PM2.5、PM10浓度有所下降。
(4)不同季节,大气能见度与PM2.5浓度的线性相关性均大于PM10。不同季节,大气能见度与相对湿度的相关性差别不大。能见度与PM2.5浓度的相关性春季最好,夏季最差,与PM10浓度相关性冬季最好,夏季最差。
(5)大气能见度与PM2.5、PM10浓度呈指数函数关系,与相对湿度呈3次方多项式关系。
(6)利用相对湿度、PM2.5、PM10浓度分不同季节对大气能见度进行非线性拟合并检验,结果表明该非线性拟合公式能较好地模拟能见度。
参考文献
[1] Charlson R J. Atmospheric visibility related to aerosol mass concentration: A review[J]. Environmental Seience and Technology, 1969, 3(10): 430-435.
[2] Baik N J, Kim Y P, Moon K C. Visibility study in Seoul, 1993[J]. Atmospheric Environment, 1996, 30(13): 2319-2328.
[3] 冯良敏,陈朝平,龙柯吉,等.成都地区2012年PM10污染过程气象条件分析[J].高原山地气象研究,2014,34(2):57-62.
[4] 邓霞君,蔡振群,项晓美,等.丽水空气污染物时序特征及与气象条件的关系研究[J].气象与环境科学,2015,38(2):60 -65.
[5] 吴雁,陈瑞敏,王颉,等.2013年河北中南部PM10和PM2.5浓度时间变化特征及其影响气象条件分析[J].气象与环境科学,2015,38(4):68-75.
[6] 吕建华,彭岩波,谢刚.2013年济南市大气能见度与相对湿度和PM10、PM2.5的关系[J].气象与环境科学,2016,39(4):93 -97.
[7] 王淑英,张小玲,徐晓峰.北京地区大气能见度变化规律及影响因子统计分析[J].气象科技,2003,31(2):109-114.
[8] 张凯,柴发合,陈义珍,等.天津武清能见度特征分析[J].气候与环境研究, 2008,13(6):800-806.
[9] 郝巨飞,张功文,杨允凌.大气能见度及影响因子特征分析[J].干旱区资源与环境,2017,31(4):160-164.
[10] 张琳,高雷娜,朱保美.德州能见度与PM2.5、PM10和相对湿度的关系[J].山东气象,2016,36(2):26-30.
[11] 宋明,韩素芹,张敏,等.天津大气能见度与相对湿度和PM10及PM2.5的關系[J].气象与环境学报,2013,29(2):34-41.
Study on the Relationship between Atmospheric Visibility and Relative Humidity, PM2.5 and PM10 in Langfang City
Zhang Xin-mu et al(Langfang Meteorological Bureau, Langfang, Hebei 065000)
Abstract To study the relationship between atmospheric visibility, relative humidity and aerosol concentrations, selected the visibility and relative humidity data of Langfang National Meteorological Observatory and PM2.5 and PM10 data of Langfang Environmental Protection Bureau from 2019 to 2021, and quantitatively analyzed their relationship. The results show that visibility was negatively correlated with relative humidity, PM2.5 and PM10 concentrations. In different seasons, the nonlinear correlation and linear correlation between atmospheric visibility and relative humidity have little difference, and the correlation coefficients were all around 0.7, the correlation in winter was slightly higher. The correlation between atmospheric visibility and PM2.5 was greater than PM10; The atmospheric visibility had an exponential function relationship with PM2.5 and PM10 concentrations and a cubic polynomial relationship with relative humidity with a correlation of more than 0.6. The relative humidity, PM2.5 and PM10 concentrations were used for nonlinear fitting of atmospheric visibility in different seasons, the results were tested. The correlation between simulated visibility and actual visibility was more than 0.95, this fitting formula can simulate visibility well.
Key words Visibility; Relative humidity; PM2.5; PM10; Fitting

