基于线性逐步回归的夏季草莓大棚内地温预测模型研究
黄龙斐 王忠 张靓 王涛 周志恒

摘要 收集2018年8—9月塑料大棚内观测的气象数据,构建了基于线性逐步回归的草莓生产大棚内的地温预测模型,采用1号大棚内的地面温度、气温、风速、总辐射,构建1个模拟方程,在构建的过程中,逐一剔除不显著的自变量。将通过信度为0.05水平的显著性检验的要素模拟出地温模型。通过2号棚的相应数据验证模型。该模型所需参数少,实用性强,模拟精度较好,可为设施夏季草莓气象服务和环境调控提供数据依据。
关键词 线性逐步回归;地温;模拟模型;夏季草莓
中图分类号:S625.3 文献标识码:B 文章编号:2095–3305(2023)09–0-03
草莓为蔷薇科,属多年生草本植物,有“水果皇后”的美誉,营养价值、经济价值都较高。作为短日照、喜冷凉气候作物,我國出产的草莓主要为冬春草莓,出产时间为每年12月—翌年5月,批发价格20~40元/kg。每年6—11月是我国草莓生产空白期,只有南半球可出产优质草莓,但受限于交通运输,目前国内优质夏季鲜食草莓市场暂为空白[1]。
川西北高原位于四川省西北部的阿坝藏族羌族自治州、甘孜藏族自治州境内,平均海拔在3 000~4 000 m以上,是四川省地势最高地区;大部分地区年均温为0~6 ℃,极端最低温在-20 ℃以下,10 ℃以上活动积温1 000~1 500 ℃·d,全年长冬无夏,春秋相连,为四川热量最低地区。而太阳年辐射量和年日照时数均为四川省最高值,丰富的光能资源在一定程度上弥补了地高天寒、热量不足的缺陷[2-6]。
通过利用高原的夏季模拟平原冬季气候,“蓝迦梅朵”团队前期经不同栽培试验,目前已成功在6—10月产出了优质鲜食草莓,并于松潘高原种植基地成功投入生产。作为植物生长的一个重要因子,气象因子是制约农作物生产产量和品质关键之一,而目前夏季草莓生产中气象要素的调控多依靠种植经验,标准化、定量化生产指导体系缺失制约了夏季草莓生产规模的扩大[7-10]。
迄今为止,针对气象条件对草莓生产的影响已有一定研究,地温是草莓生长指标中非常重要的气象要素,但现有研究多是针对冬春草莓开展的,对高原草莓设施生产,尤其是夏季草莓的生产研究鲜见报道。拟通过“蓝迦梅朵”夏季草莓基地1号、2号实验大棚小气候数据(1号、2号棚为相邻,规模一样,品种一样,施肥施水一样的2个实验棚),建立适于草莓设施栽培的地温预报模型,为草莓成熟期预测、产量预测及设施杨梅气象保障服务提供技术支持。
1 资料和方法
1.1 试验资料
草莓在5 ℃以上开始发芽,最佳生长温度为15~25 ℃。如果外界温度低于10 ℃或高于30 ℃,草莓的生长将受到严重抑制,甚至不会生长或死亡。如果草莓生长过程中温度降至7 ℃以下,植物会冻死。草莓根在2 ℃和10 cm的温度下开始适当的生产活动,在10 ℃时更为活跃,生长速度非常快。
根据相关调查的统计数据,土壤温度与草莓成熟度和产量密切相关。在冬季最冷的季节,温度越低,草莓相应的预收获越低,但总产量最高,草莓果实也越大,反之亦然。如果温度更高,草莓的早期产量虽然高,但总产量很低,果实也很小。温室种植草莓一般在7月底进行翻耕、浇水、密封,保持温度在70 ℃左右,可以起到杀菌作用,减少病菌。通常持续15 d,然后通风。为了获得高产,必须种植高穗,将草莓种植穗设置在90 cm的距离,双排种植,穗高控制在25~30 cm之间,穗宽25~30 cm,种植前7 d浇水。最好选择阴天种植,有条件的选择窝盘苗木较好,移植后存活率高,苗木速度慢,结果早。种植时,树苗种植深度必须掌握为“深埋不深,浅埋不露根”,种植后必须一次性足量浇水。
1.2 试验方法
试验时间为2018年8月—9月,此时草莓处于花芽萌动至果实成熟期,是产量和品质形成的关键期。试验地点位于四川省松潘县水晶乡,选择2个塑料大棚,大棚呈南北向,长17 m,宽8 m,肩高1.5 m,顶高3.5 m,棚内有约1 000株草莓,品种是蒙特瑞。地形为高原,海拔约3 100 m,土质为沙壤土、微酸性、中等肥力。大棚中心位置距地1.5 m处建有1套ZXCAWS380农业气象站,1个温湿传感器模块,观测要素为气温、相对湿度、总辐射、光合、地温、土壤3参数(10、20、30 cm)水电导率、风速,采集频率为1 min/次,存储每1 min的平均值。大棚内温度湿度采集频率为5 min/次。
此次试验数据为所有要素的小时数据,温湿数据采用5 min/h数据平均值。按时间顺序记录的连续数据序列,例如:计算机数据收集系统是一个时间序列,温室气体环境控制系统每隔一段时间收集的温度数据是一个时间序列,这是一个独立的时间序列。因此,使用时间序列分析方法的具体步骤预测温室温度。分析原始室内温度数据的序列,并使用线性差法处理异常和缺失数据。为了消除周期性影响,每年对处理过的温度数据集进行区分。在微分温度序列之后,对相关系数进行估计,以确定其是否稳定。如果没有,则进行另一个顺序差分,然后进行平滑性测试;针对平滑序列,模型类型是根据自相关系数的估计和部分相关系数的估计选择的。微分后估计均匀时间序列预测模型。如果预测模型不符合要求,修改预测模型并重复步骤,直到获得令人满意的室内温度预测模型。
1.3 模型的构建
逐步回归,剔除不显著的自变量。在建立多元回归方程时,通常有一些自变量与依变量存在着显著的回归关系;而另些自变量对依变量的影响很小,与依变量不存在的回归关系,这些自变量在回归方程中是不重要的,应进行剔除,使建立的多元线性回归方程中仅包含与依变量存在显著回归关系的自变量,此时建立的多元线性回归方程称为最优多元线性回归方程。
利用软件IBMSPSSStatistics,将1号大棚内的地温作为因变量,气温、相对湿度、风速、总辐射作为变量,建立四元线性回归方程。可以看出变量气温、相对湿度、总辐射回归系数不显著,在建立最优线性回归方程时需要剔除,由于变量之间的相关性,要逐一剔除,先剔除相关性最低的风速。
去掉风速后建立三元线性回归方程,3个变量的相关系数都<0.05达到显著水平,不需要进一步剔除变量,最终的最优线性回归方程为:
Y1=6.347+0.197×T+0.065×RH+
0.037×Ra(1)
式(1)中,Y1是1号棚模拟地温(℃),6.347为常量,0.197为温度系数,T为温度(℃),0.065为湿度系数,RH为相对湿度(%),0.037为总辐射系数,Ra为总辐射(W/m2)。
1.4 验证模型
为了验证模型的精确度,应用2号大棚的温度、相对湿度、总辐射代入公式,将得出的Y(模拟地温)与2号棚实际地温进行对比。
Y2=6.347+0.197×T+0.065×RH+0.037×Ra(2)
式(2)中,Y2是2号棚模拟的地温(℃),6.347为常量,0.197为温度系数,T为温度(℃),0.065为湿度系数,RH为湿度(%),0.037为总辐射系数,Ra为总辐射(W/m2)。
2 结果与分析
2.1 地温分别与气温、相对湿度、总辐射、风速的关系
2.1.1 地温与风速的关系 在建立模型时,风速因为相关性最低被剔除,这是由于大棚内通风口小,风对地温的影响相对其他要素要小。
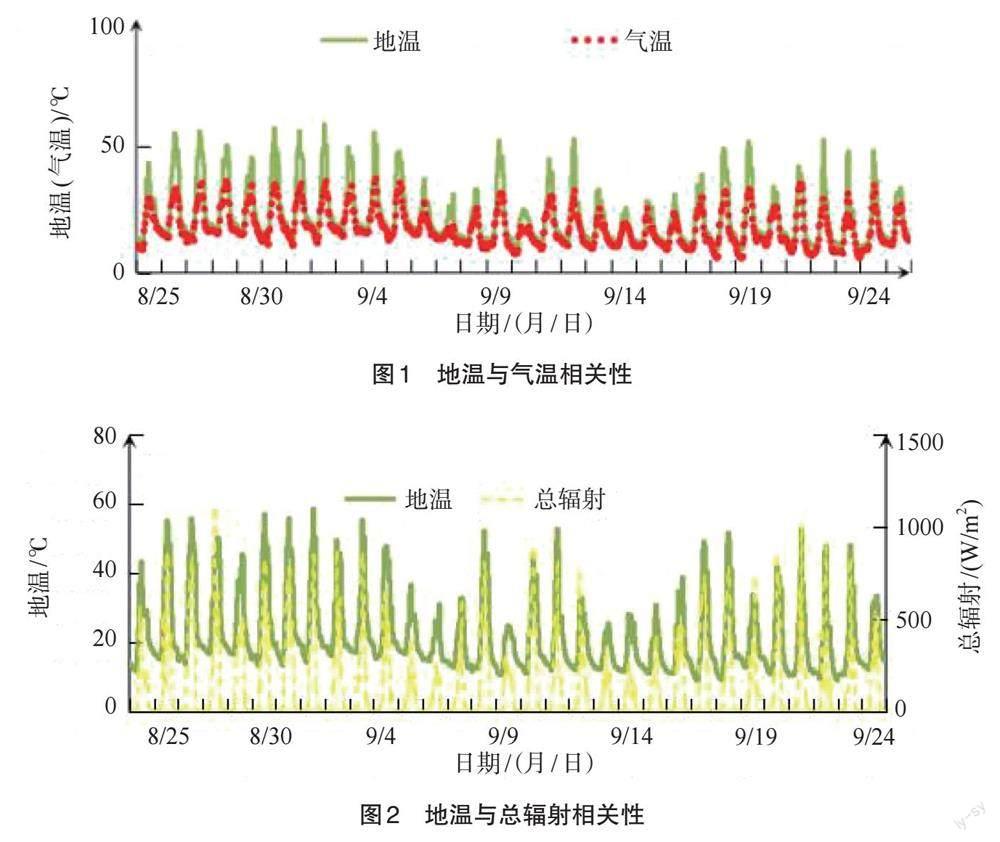
2.1.2 地温与气温的关系 由图1可知,整个实验期内,地温与气温呈正相关,其中,在白天正午气温在30 ℃以上时,地温比气温明显偏高,夜间气温比地温稍微偏低。
2.1.3 地温与总辐射的关系 由图2可知,整个实验期内,地温与总辐射呈正相关,其中,在白天12:00或者地温在30 ℃以上时,总辐射越高地温越高,而在夜间,总辐射越低地温越低。
2.1.4 地温与相对湿度的关系 由图3可知,整个实验期内,地温与相对湿度呈负相关,相对湿度越高、地温越低,反之,相对湿度越低、地温越高。
2.2 模拟地温与实际地温的对比验证
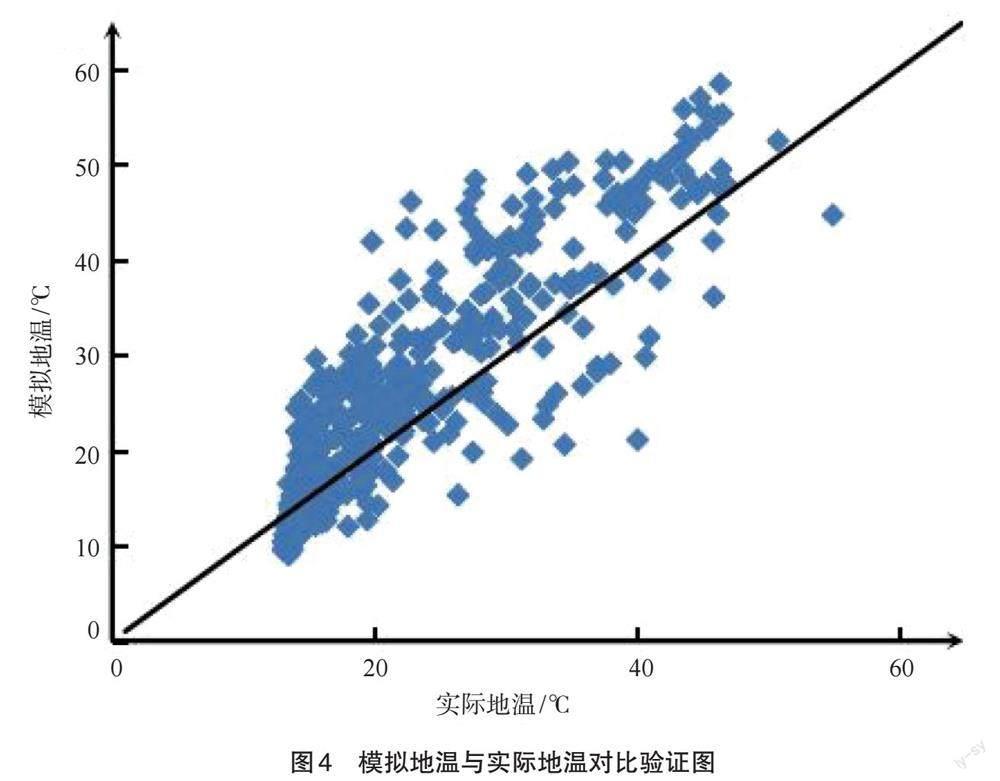
在实验期间,将1号棚的地温作为因变量,气温、相对湿度、总辐射、风速作为变量,在剔除风速之后,利用三元线性回归方程得到模型的模拟地温Y1。为了验证模型的可用性,将2号棚气温、相对湿度、总辐射代入公式,得到模拟地温与2号棚实际地温作折线图1:1对比。由图4可以看到,在温度10~30 ℃时,模型的模拟效果较好,模拟地温与实际地温相对集中,且大多数集中在1:1线附近。而在温度30~50 ℃时效果较差,数据较为分散。而在50 ℃以上,数据又相对较集中,但温度超过50 ℃的情况较少。总体来说,此次实验的模型精度较好。
3 讨论与结论
研究建立了1个基于线性逐步回归的大棚草莓的地温模型,可以利用棚内气温、相对湿度、总辐射等气象要素作为模型变量,最后得出模拟地温。通过另外1个大棚验证模型效果。结果表明:模型预测精度较好。但在30~50 ℃之间的精度不是很好。主要是由于变量比较少,数据量不够多,时间不够长,且地温还与地面湿度、浅层地温、湿度等其他气象要素有关。
线性逐步回归模型是建立在大量实验数据基础上的,模拟某一特定条件下的温室小气候,其精度较好。但线性逐步回归只能采集于特定环境、特定时间,不具有普遍代表性,因此,模型只限于解决某一特定时间、特定环境的小气候问题,其广泛适应性还有待进一步研究。
此处建立的大棚棚内草莓地温预测模型的模拟地温只是针对草莓大棚,对其他不同类型大棚小气候模拟还需要通过大棚内外气象要素的对比试验数据调整模型参数。线性逐步回归构建立了大棚内地温模拟模型,可以利用气温、湿度、辐射为草莓生产管理提供科学依据。但设施草莓生产中,瞬时地温对草莓的生长非常重要。而且影响大棚内小气候因素除了外界气象要素外,草莓植株的株高和茎粗、叶面积也会直接影响蒸腾量大小,从而影响潜热,在以后的试验中还需要进一步完善模拟模型,同时增加短时间气温(如5、10 min等)的模拟,还有在地面铺塑料膜时的模拟,其结果将更具实用性。
参考文献
[1] 金志凤,符国槐,黄海静,等.基于BP神经网络的杨梅大棚内气温预测模型研究[J].中国农业气象,2011,32(3):362-367.
[2] 张新颜,王颖,张盼,等.基于SVR的塑料大棚坐果期草莓光合速率预测模型研究[J].农业工程技术,2021,41(16):57-59.
[3] 杨栋,李清斌,孙军波,等.大棚草莓品质模型及品质时空变化特征[J].浙江农业科学,2016,57(11):1904-1908.
[4] 楊文刚,孟翠丽,胡幼林,等.春季不同结构温室气温变化特征及预测模型[J].江苏农业科学,2015,43(6):386-390.
[5] 何涛,廖克杰,陈丹,等.线性回归模型在四季大棚小气候预测方面的应用研究[J].安徽农业科学,2012,40(19):10061 -10062.
[6] 杨义,洪波,李艳莉,等.基于2种算法的日光温室日均气温预测模型比较研究[J].陕西气象,2022(3):48-52.
[7] 罗靖,杨再强,杨立,等.基于高光谱参数建立苗期高温条件下草莓叶片叶绿素含量估算模型[J].中国农业气象, 2022,43(10):832-845.
[8] 金志凤,符国槐,黄海静,等.基于BP神经网络的杨梅大棚内气温预测模型研究[J].中国农业气象,2011,32(3):362-367.
[9] 高羽,李静,刘洋,等.结构方程模型在兴安落叶松林生长中的应用[J].南京林业大学学报(自然科学版),2023,47(1):38-46.
[10] 张利亚,刘霞,师豪,等.木醋液对大棚草莓土壤pH、叶绿素、品质及产量的影响[J].中南农业科技,2022,43(1):22-23,27.
A Study on the Prediction Model of Temperature in Strawberry Greenhouses in Summer Based on Linear Stepwise Regression
Huang Long-fei et al(Aba Prefecture Meteorological Observation Center, Ma’erkang, Sichuan 624000)
Abstract Collected meteorological data observed in plastic greenhouses from August 2018 to September 2018, and constructed a ground temperature prediction model for strawberry production greenhouses based on linear stepwise regression. A simulation equation was constructed using the ground temperature, air temperature, wind speed, and total radiation in greenhouse 1, and insignificant independent variables were removed during the construction process.The elements that have passed the significance test with a reliability of 0.05 level should be simulated into the ground temperature model. Then validate the model using the corresponding data from shed 2. This model requires fewer parameters, has strong practicality, and good simulation accuracy, which can provide data basis for strawberry meteorological services and environmental regulation in summer facilities.
Key words Linear stepwise regression; Ground temperature; Simulation model; Summer strawberries

