指向深度学习的高中物理实验教学——以有趣的硬币碰撞为例

李茹新 陈晓陆 皮永旺

(1.北京市朝阳外国语学校,北京 100012;2.中国人民大学附属中学朝阳学校,北京 100012)

深度学习是指学生在教师的引导下,围绕素养导向的学习目标,聚焦引领性学习主题,展开有挑战性的学习任务与活动,全身心积极参与、建构学科知识、体会学科思想与方法,获得终身发展的有意义的学习过程.[1]目前,深度学习已成为各学科教学实践和研究的焦点,是落实立德树人、落地核心素养的重要途径.物理学科是一门以实验为基础的自然学科,在课堂开展富有创造性的物理实验教学可以有效促进深度学习.

1 本节课的授课背景

1.1 学生现有知识储备

学生在本节课前,已经对碰撞有了一定的学习,了解弹性碰撞和非弹性碰撞的概念,能够从动量和能量的角度对碰撞进行一定的定量分析.除此之外,通过拓展性学习,学生还了解了恢复系数的概念.

1.2 将“硬币碰撞实验”引入课堂的几点思考

(1)两个具有相对运动的宏观物体或微观粒子在很短时间内的相互作用过程称为碰撞.由于碰撞时间很短,内力往往很大.然而对于上述事实,学生很难真正接受,更多的学生是停留在记忆层面,究其原因是学生在建立碰撞概念时缺乏直观的亲身体验,这是利用硬币碰撞能够解决的问题之一.

(2)对于不同的碰撞,求解的方法并不同,这在一定程度上突出了不同碰撞之间的区别,但是削弱了碰撞之间的共性.再加之学生日常接触的多数题目都属于经过命题者思维加工后的,即完全弹性碰撞和完全非弹性碰撞这两种理想化模型,久而久之,学生便有了_思维定式.硬币碰撞是一个实际问题,通过适当的问题驱动学生思考,可使学生对几种不同的碰撞有一个整体的把握.

(3)与台球的碰撞相比,利用硬币在桌面上的二维碰撞可以更简单地让每一位学生获得对二维碰撞的直观感知.通过对二维碰撞的简单分析,可以进一步深化并拓宽学生对动量守恒定律矢量性的理解.

2 课堂主要环节的实施

环节1:碰撞特点的再认识.

任务1:如图1所示,取4枚1元硬币A、B、C、D,B、C、D放在水平桌面中间,作为被碰物.用食指在硬币A上方拨动,使其以较大速度与B发生正碰(注意碰前食指要离开硬币A),观察现象并解释.

图1

学生:观察到碰撞后A、B、C静止,D获得一速度向前运动一段距离,并用两质量相等的物体发生全弹性正碰会有“速度交换”的规律来解释.

追问1:认真观察倒数第2个硬币C是真的不动吗?

学生:重做实验后发现倒数第2个硬币C确实有向前的微小移动.

追问2:那么倒数第2个硬币C为什么会动呢?

学生讨论并结合硬币碰撞过程的vt图像(如图2所示)给出解释:可能是硬币弹性不是特别好,这将导致倒数第2个硬币C与倒数第1个硬币D碰撞的过程中还没有到达时二者就分离了,此时硬币C的速度还没有减为0.

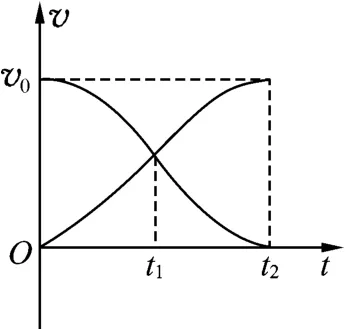
图2

追问3:如果用右手食指用力向下按住B,使A仍以较大速度沿B、C、D中心连线方向与B发生正碰,会发生什么现象呢?

学生:可看到,用力按住B,仍可观察到碰撞后A、B、C几乎静止,D获得一速度向前运动一段距离.

追问4:也就是说有无手指按住B,观察到的现象几乎没有区别.这又说明什么呢?

学生讨论得出:用手指按住B时,A、B碰撞过程,地面及手指对系统的摩擦力大大增加,但由于碰撞时间极短,A、B及B、C间的作用力仍远大于摩擦力(A对B的极大作用力手指能感觉到),仍然满足动量守恒的条件.

设计意图:通过对倒数第2个硬币C为什么会动的细致观察与思考,驱动学生从运动和相互作用的角度还原出碰撞是一个先压缩再恢复的动态过程,在头脑中建构合理的物理图像,并使学生体会弹性碰撞只是一个形变能够完全恢复的理想化过程模型.在分析实际问题时,也应该考虑碰撞物体的弹性好坏.通过观测用力按住硬币B之后碰撞结果,学生亲身体验小小硬币碰撞过程中的相互作用力,并获得碰撞过程内力非常大的实验事实证据.

环节2:设计实验比较不同硬币的质量大小.

任务2:外出旅游时,经常会带回一些不同的硬币.如图3所示,这些硬币质量往往不同.在没有天平的情况下,能否通过碰撞来比较两个硬币的质量大小?

图3

生1:让一个运动的硬币去正碰静止的硬币,如果碰撞后入射硬币不反弹,则入射硬币质量大于被撞硬币质量;如果碰撞后入射硬币反弹,则入射硬币质量小于被撞硬币质量.

生2质疑与反驳:上述分析只有在弹性碰撞下才成立,实际上两个硬币具体的材质未知,不能默认为是完全弹性碰撞.如果两枚硬币的弹性不是特别好,即使是用质量小的硬币去正撞击质量大的硬币,也有可能会发生入射硬币不反弹的现象,因此通过一次碰撞不一定能比较两个硬币的质量大小.

生3:既然一次碰撞不行,那么能否用互换的思想(如图4所示)比较出哪个硬币质量大?

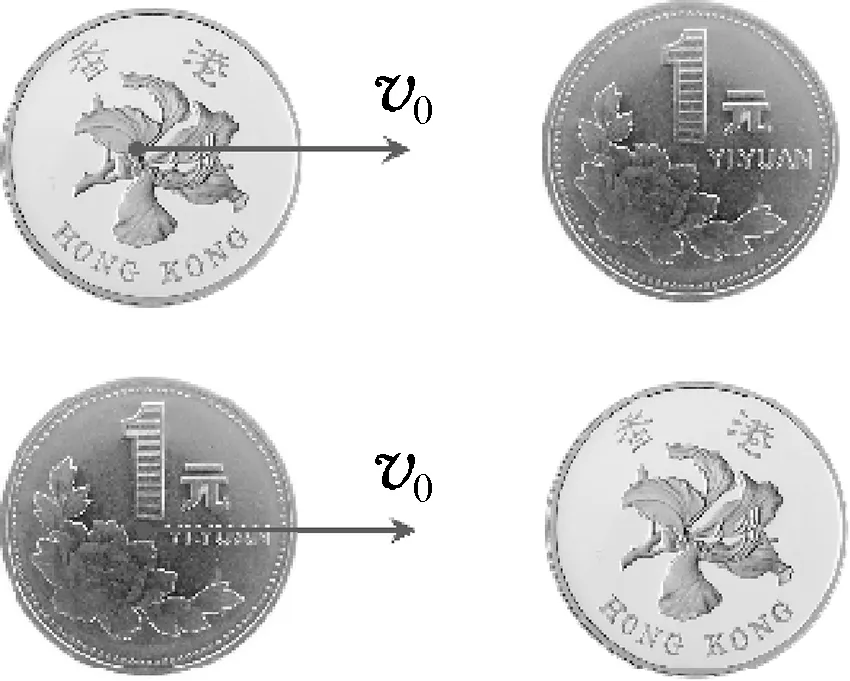
图4

教师给予鼓励,并结合图3组织学生讨论在入射硬币初速度不变的情况下,两种情况下的碰撞结果是否会有不同呢?

生4:肯定会有不同!当入射硬币质量较大时,被撞硬币获得的速度大;进而可发现当入射硬币质量较小时,被撞硬币获得的速度小.因此我们可以通过观测被撞硬币在桌面上滑行的距离来比较硬币的质量.

教师对学生优秀的物理直觉给予鼓励,并引导感兴趣的学生在课后对生4的猜想给出证明.

设计意图:通过对一次碰撞能否比较出两枚硬币的质量大小的争论,评价学生是否能在环节1的启迪之后将硬币的弹性因素考虑进来,进一步强化碰撞物体的弹性对碰撞结果的影响.通过利用互换思想比较硬币质量,培养学生的物理直觉,激发学生的进一步探究欲望.需要说明的是,考虑到学生实际水平和课堂时间的限制,在生4提出通过观测被撞硬币的滑行距离来比较硬币的质量大小后,并没进行理论上的严格分析.实际上该学生的观点也不难证明,简要说明如下.设入射硬币碰撞前后的速度分别为v10和v1,被撞硬币碰撞前后的速度分别为v20和v2,恢复系数为e,质心速度为vC.根据一维碰撞的一般结果有v1=(1+e)vC-ev10,v2=(1+e)vC-ev20.则在入射硬币初速度v10不变,v20=0的情况下,有v1=(1+e)vC-ev10,v2=(1+e)vC.容易发现当入射硬币质量较大时,质心速度vC大,被撞硬币碰撞后的速度v2大,在忽略桌面与各硬币之间动摩擦因数的差异时,被撞硬币滑行的距离会远一些.

任务3:如果近似认为不同硬币之间碰撞为弹性碰撞,并忽略各硬币与桌面之间的动摩擦因数的差异,能否通过碰撞来测得一枚未知硬币的质量?实验提供的器材有:两枚已知质量的硬币,刻度尺,装有弹簧的弹射装置.

学生分组讨论,设计实验方案,汇报如下.

如图5所示,利用弹射装置使未知质量的硬币mx获得一定的速度v,使其去撞击静止状态的已知质量的硬币m1,根据弹性碰撞的规律可得,被撞硬币在碰撞后瞬间的速度为

图5

同样的操作,利用弹射装置使未知质量硬币mx获得相同的速度v,使其去撞击静止状态的已知质量的硬币m2,根据弹性碰撞的规律可得,被撞硬币在碰撞后瞬间的速度为

教师对学生提出的方案给予鼓励,并介绍1935年英国物理学家查德威克巧妙地利用中子与已知质量的氢核和氦核分别发生碰撞,成功测定中子质量的经典案例.

设计意图:通过设计性的任务,让学习更主动,培养学生创新能力.通过介绍与中子发现的相关物理学史,使学生体会到科学就在身边,提升学生的学习成就感.

环节3:探究硬币的斜碰规律.

任务4:如图6所示,让两枚质量相等的1元硬币发生斜碰,观察碰后两球的速度夹角有何规律,请你建立合理的模型,证明这个结论.

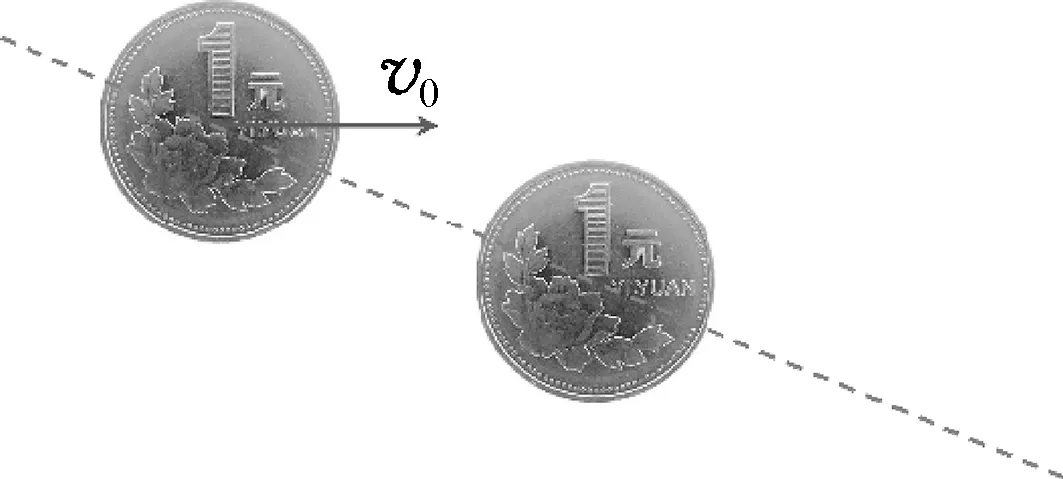
图6

学生实验发现,两球在发生斜碰时,碰后两球的速度夹角总是接近90°.教师提示可先从最简单的情况入手研究,建立弹性碰撞过程模型.

小组讨论,得出以下3种分析.

方法1:以水平方向为x轴,竖直方向为y轴.[2]

如图7所示,碰前入射硬币1的速度记为v0,碰后硬币1、2的速度分别记为v1和v2,v1和v2与x轴夹角分别记为α和β.

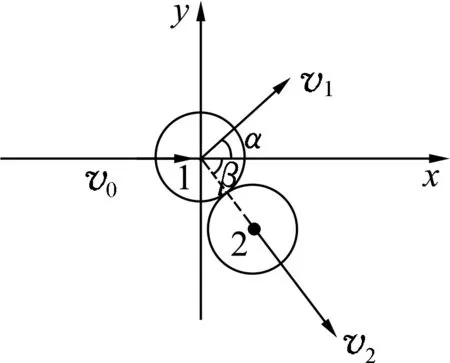
图7

根据动量守恒定律可知,在x方向

在y方向

式(1)(2)联立可得

又由机械能守恒定律

式(3)(4)联立可得cos(α+β)=0,即α+β=90°.

方法2:将运动分解到连心线和垂直于连心线的方向处理.

如图8所示,碰前入射硬币1的速度记为v0,碰后硬币1、2的速度分别记为v1和v2,v1和v2与硬币1初速度v0方向夹角分别记为α和β.

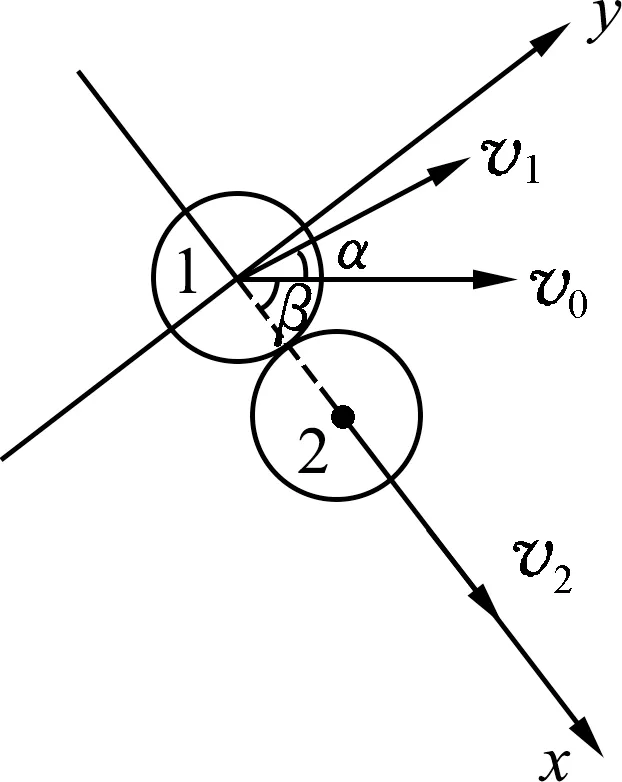
图8

根据动量守恒定律可知,在x方向

y方向

式(5)(6)联立可得

又由机械能守恒定律

式(7)(8)联立可得cos(α+β)=0,即α+β=90°.

方法3:不建坐标系,借助动量三角形处理.

碰前入射硬币1的动量记为p0,碰后硬币1、2的动量分别记为p1和p2,p1和p2与硬币1初动量p0方向夹角分别记为α和β,两硬币碰撞前后的动量矢量三角形如图9所示.

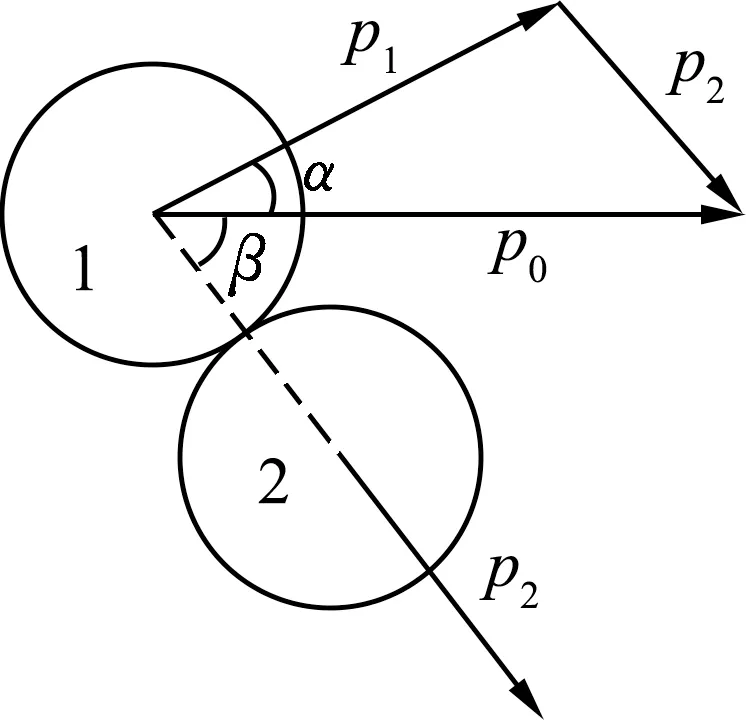
图9

由余弦定理可知

p02=p12+p22-2p1p2cos[π-(α+β)].

考虑到两硬币质量相等,有

又由机械能守恒定律有

式(9)(10)联立可得

cos(α+β)=0,即α+β=90°.

设计意图:通过对等质量硬币二维碰撞的分析可以让学生认识到对于碰撞问题,同样可以根据需要建立坐标系,利用分解的思想进行运算,也可以直接利用动量矢量图进行求解,开阔了学生的视野,激发学生的创新思维.在此环节还可引导学生思考,若有机械能的损失,则碰后的两球运动方向所成的夹角是否还等于90°,激发学生对该问题的进一步思考.

3 结语

本节课学生在教师的引领下,通过简洁的实验探究、深度的交流思辨、巧妙的设计性任务、严谨的科学论证等活动,有效地解决了课前存在的教学问题,达成了教学目标,同时也充分地调动学生主动地迁移应用已有知识、方法解决实际问题,让深度学习真的发生,并使学生从课堂中体验到物理带来的学习乐趣.