考虑破坏深度和发电保证率的水风光互补调度规则研究
景 含,陈 翔,孟洪文,刘本希*
( 1.大连理工大学水利工程学院,辽宁 大连 116024;2.水利部珠江水利委员会珠江水利综合技术中心,广东 广州 510611;3.云南大唐国际李仙江流域水电开发有限公司,云南 普洱 665000)
随着“3060”双碳目标的提出,中国可再生能源取得了快速发展,成为全球可再生能源容量增长的主要推动力之一[1]。充分利用水、风、光可再生能源是构建新型电力系统和实现双碳目标的重要途径。然而,风、光电源出力的随机性对电网安全稳定运行提出了极大的挑战。水电作为启停迅速、运行灵活、技术成熟的优质电源,风、光高速发展背景下,开展水、风、光联合调度研究对于提高清洁能源发电效益和电力系统安全稳定水平具有重要意义[2]。
考虑到风光出力的不可控性,水风光互补调度是在电网安全运行的前提下,最大可能地挖掘互补调度的优势和潜力,提高总体发电效益。目前,水风光短期互补调度主要是平抑风光出力波动性,而中长期调度则是侧重系统的发电效益[2]。谢航等[3]提出水风光短期互补调度策略,从“源源互补”和“源荷匹配”2个角度构建模型,分别采用花粉算法与逐步优化算法优化求解,最后通过分析互补效果,总结水风光短期调度策略;孙艺轩[4]基于水风光互补特性提出等效电站模型,并将等效电站模型与等效负荷模型进行对比讨论,验证了等效电站模型在调峰效果与风光负荷平抑方面的有效性。
大规模风、光并网之后,水电将逐步由传统电源转变为调节电源[5],传统的水电调度规则将不再适用[6-7],因此需要研究适用于风、光大规模并网后的水风光联合调度规则。已有部分学者开展了水电与新能源联合调度规则研究。沈筱等[8]建立了以系统发电量最大为目标的水风光长期互补调度模型,通过BP神经网络提取调度规则,并验证了该规则能较好地保留互补系统的发电效益;魏获晴[9]针对大规模风光并网挤占通道问题,提出了考虑输电断面限制、季调节以上水电站主调模式下的水风光长期互补优化调度模型,通过实例分析验证所提模型能够增加系统总的发电量,提高送电通道的利用率。然而,水、风、光的发电能力均易受天气影响,极端气候条件下将严重威胁电力系统安全稳定运行。如2022年中国川渝地区遭遇了干旱和持续高温,造成水电站出力的深度破坏,地区用电极度紧张的情况。因此,水风光联合调度规则在满足发电保证率的同时[10],还需要避免气候影响条件下出力深度破坏。
为此,本文提出了考虑发电保证率和出力破坏深度的水风光长期联合调度模型。将发电保证出力要求处理成0~1变量,考虑系统破坏深度系数以限制极端破坏,并采用混合整数非线性规划模型进行求解。通过对长系列历史数据进行模拟调度得到训练样本,利用神经网络学习得到调度规则[8-9]。通过对西南某流域下游梯级水电站及风、光电源实例研究表明,本文所得调度规则能够得到良好的发电效益,满足发电保证率要求,并避免出力深度破坏。
1 水风光长期互补优化调度模型
1.1 目标函数
将地区并网的风电、光伏电源分别考虑为一个整体,建立以水风光发电量最大为目标的模型,目标函数为:
(1)

1.2 约束条件
水量平衡约束:
Vi,t+1=Vi,t+(Qi,t-qi,t)Δt
(2)
式中Vi,t、Vi,t+1——第i座水库t时段初、末的蓄水量,万m3;Qi,t——第i座水库t时段的入库流量,m3/s;qi,t——第i座水库t时段的出库流量,m3/s。
出库流量约束:
(3)
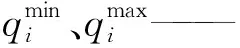
发电流量约束:
(4)
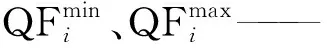
梯级水库之间的联系:
Qi+1,t=QJi+1,t+qi,t
(5)
式中 QJi+1,t——第i座水库与第i+1座水库t时段的区间入流量,m3/s。
水电站出力约束:
(6)
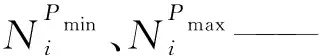
水位约束:
(7)
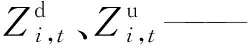
输送通道容量约束:
(8)
式中Amax——外送通道容量限制,MW。
发电保证率约束:
(9)
其中:
(10)
式中Np——水风光联合保证出力;β——发电保证率;bt——判断是否满足保证出力的0~1变量。
破坏深度约束:
(11)
式中α——水风光联合保证出力破坏深度系数。
1.3 风光出力
1.3.1风电出力估算
风能估算方法众多,有采用数理统计来预测风电功率的方法[11];还有根据风机功率-风速关系曲线得到的风频率法[12]。本文参考菲利普贝特计算风电功率的方法[13-14],该方法计算方式简便,并且所需数据较少,容易获取。该方法认为风速达到“切入”风速时,风力发电机开始供电;当风速达到额定功率风速时,发电机以额定功率发电;当风速大于“切出”风速时,风力发电机停止供电。具体计算见式(12):
(12)
式中 NWt——t时段的风电出力,MW;vt——t时段的风速,m/s;IW——风电装机;vcut-in——切入风速;vcut-off——切出风速;vrated——额定风速。
1.3.2光伏出力估算
光伏发电是一个多变量耦合的非线性的随机过程,光照强度、日照时数、环境温度、组件温度以及气压、湿度等都会对光伏功率产生影响[15]。本文采用传统的光伏出力估算方式,认为光伏输出主要与光伏组件的性能、辐射强度和温度有关[14],计算式如下:
(13)
(14)
式中 NPstc——标准条件下光伏板的额定输出功率;Rstc——标准条件下的辐射强度;TPnoc——光伏板的额定工作温度;TPstc——标准条件下的温度;Rt——周期t的实际辐射强度;α——光伏板的功率温度系数;TPt——光伏板在周期t的实际温度;Temt——t时段气温。
2 调度规则提取
2.1 神经网络
2.1.1BP神经网络
BP神经网络是一种前馈神经网络,能够基于数据样本之间的特征,提取之间的规律并进行记忆处理。BP神经网络已经在水电调度规则[16]、水力发电预测[17]、径流预报[18]等领域得到了广泛应用。本文采用BP神经网络对多能互补长期历史数据模拟调度进行挖掘,提取联合调度规则。首先,把模拟调度数据分为训练集、验证集,并采用交叉验证来避免固定划分数据集的局限性和特殊性。通过确定性系数来判断模型的准确度,并且进一步通过量化指标均方根误差RMSE和平均绝对误差百分比MAPE来评判神经网络的拟合精度。
2.1.2输入层和输出层
根据优化调度模型结构及计算过程,考虑到需要统计各种调度方式下的出力结果,本文将水库的出力作为神经网络的输出层。初步认为时段初各水库水位、区间流量以及上游电站的出力、接入的风光出力都会对决策变量产生影响,并通过灰色关联分析进一步筛选。
2.1.3输入输出数据处理
为了便于不同单位或量级的指标能够进行比较和加权,需要将数据进行归一化处理,因此,本文对输入输出数据进行归一化处理来为后续神经网络的训练提供基础。
2.2 基于灰色关联分析的输入因子筛选
灰色关联分析是指对变量和影响因素之间的相关程度进行分析从而评判出影响因素主次关系的一种方法。灰色关联度分析对于一个系统发展变化态势提供了量化的度量,非常适合筛选影响因子。本文采用灰色关联分析方法筛选神经网络输入因子,具体步骤如下:①确定分析数列,反应系统行为特征的定为参考数列,影响系统行为的定为比较数列;②变量的无量纲化;③计算关联系数;④计算关联度;⑤关联度排序,关联度越大,比较数列对参考数列的影响越大。
根据上述分析,本文总体求解流程见图1。
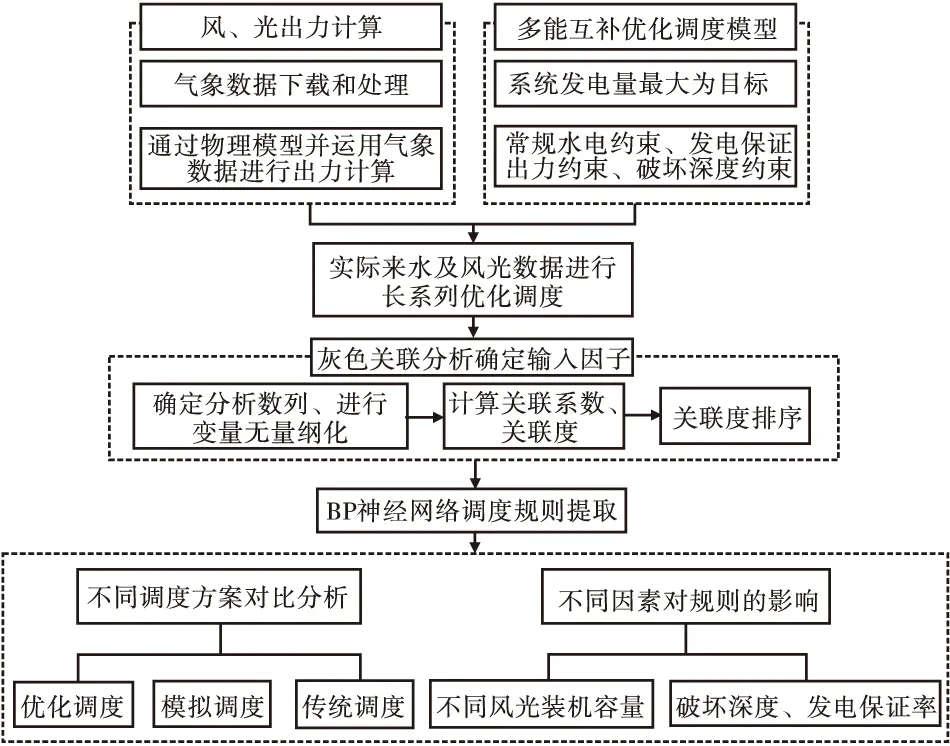
图1 总体求解流程
3 实例分析
3.1 工程背景
本文以中国西南地区A省某流域的梯级水库群为实例研究对象,PS1、PS2、PS3、PS4、PS5、PS6为该流域已建成的6级电站。其中,PS2、PS5分别具有不完全多年调节和多年调节能力,其余仅进行日调节或者季调节。本文以PS2、PS5为典型工程,考虑该流域周边接入的风能、太阳能资源进行联合优化调度。其中PS2、PS5主要参数见表1。
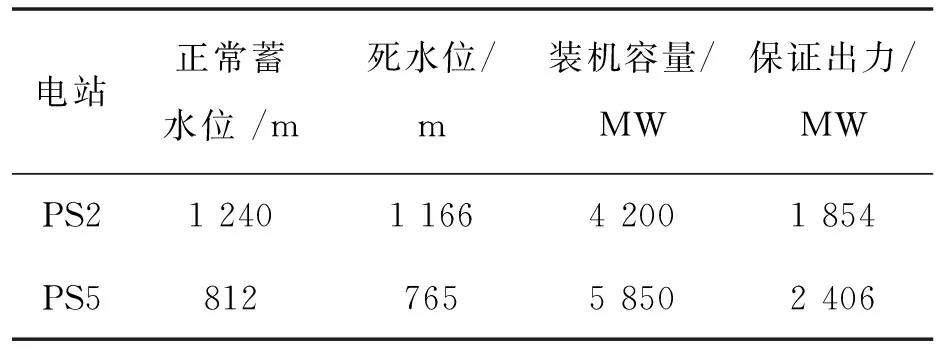
表1 PS2、PS5主要水能参数
3.2 风、光出力计算
为推动绿色电源建设,优化能源结构,A省布局建设新能源,目标在“十四五”期间新增“800万千瓦风电+300万千瓦光伏”,本文考虑A省研究流域周边规划的2 000 MW的风电和750 MW的光伏。在出力估算方面,从ERA5获得从1979—2018年每天的小时再分析气象数据,通过1.3所述方法计算风电、光伏逐小时平均出力,并统计得到1979—2018年每月平均风电、光伏出力,以及多年风光平均出力(图2)。从图2可知,风电出力在1—3月较大,4—10月逐渐下降,随后从9月开始进入秋冬季风电出力又开始增大。光伏出力从1—4月逐渐上升,4—12月逐渐下降。
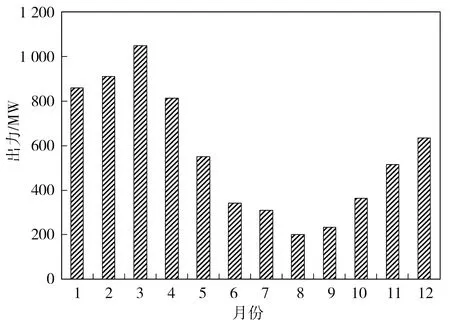
a)风电
3.3 历史数据模拟调度结果
本文采用1979—2018年电站实际来水以及3.2节估算的风光出力进行模拟调度,其中系统保证出力为水电保证出力加上10%的风光装机,破坏深度系数为0.6,发电保证率为90%。从第2节所建立的模型中可知,由于水电的水位库容关系曲线、尾水位泄量曲线属于非线性约束,并且计算保证率的时候还引入0~1变量,因此属于混合整数非线性规划模型,本文采用Lingo 18.0进行求解。图3a、3b、3c分别展示了PS2、PS5模拟调度多年平均水位变化过程和出力过程,表2展示了水风光互补运行模式下多年平均发电情况。

a)PS2水位过程
从图3c可以看出11月至次年5月风、光电出力较高、水电出力较低;而在5—10月,水电来水较大,出力较高,而风、光电出力则较低。从图3a、3b可知,PS2、PS5均充分发挥了良好的调蓄作用,汛前腾出库容,而汛期快速提高水位,给风、光留出输电通道,避免弃水。总体上,水、风、光之间实现了良好的季节互补性。从表2可以看出,水风光联合调度多年平均发电量为510.44亿kW·h,并且通过水风光联合调度能满足90%的发电保证率要求和避免系统深度破坏,因此水风光联合优化调度能保持更好的发电效益同时充分促进清洁能源的消纳。
3.4 调度规则提取
3.4.1输入和输出的选择


表3 PS2灰色关联系数结果

表4 PS5灰色关联系数结果

表5 PS2、PS5神经网络输入层和输出层选择
3.4.2调度规则提取
结合3.3历史数据模拟调度结果,通过3.4.1筛选出的输入和输出带入BP神经网络进行训练,训练占比设为0.7,交叉验证设为5折。具体的训练评价指标结果见表6、7。

表6 PS2神经网络拟合结果
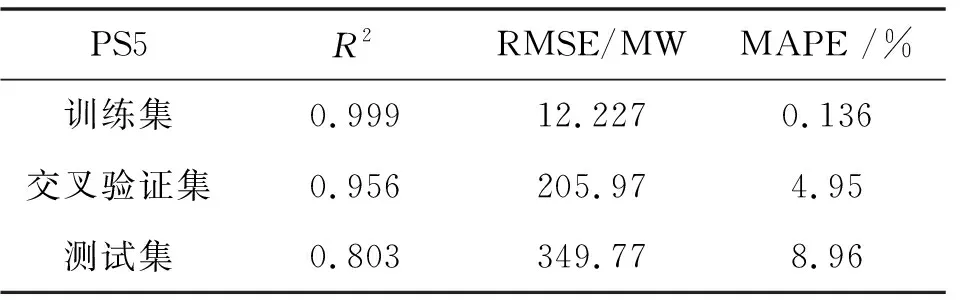
表7 PS5神经网络拟合结果
从表中可知,PS2、PS5网络测试集的均大于0.8,MAPE基本都低于10%,说明模型的拟合准确度较高。因此,模型的训练结果较好,可以用来指导进一步的模拟调度。
3.5 不同方案结果分析
为了验证所提方法的有效性,根据历史数据模拟生成40 a的梯级来水,模型的发电保证率设置为90%,破坏深度系数设置为0.6,对以下3种不同方案进行对比分析。方案1:理想情况下考虑破坏深度和发电保证率的水风光联合优化调度;方案2:通过神经网络提取的调度规则进行的模拟调度;方案3:基于调度图的传统调度。
3.5.1不同调度方案对比分析
表8展示了3种方案对应的发电量以及保证率、最低破坏出力和弃水情况,图4展示了3种方案下PS2、PS5的水位及出力过程。从表8可知,理想调度得到的发电量最大,并且保证率和最低破坏出力都能满足设计要求,基于神经网络调度规则得到的发电量、保证率、最低破坏出力和弃水量次之,但是与理想调度方案结果差异不大,而基于常规调度图得到的发电量最小且保证率和最低破坏出力都不理想。
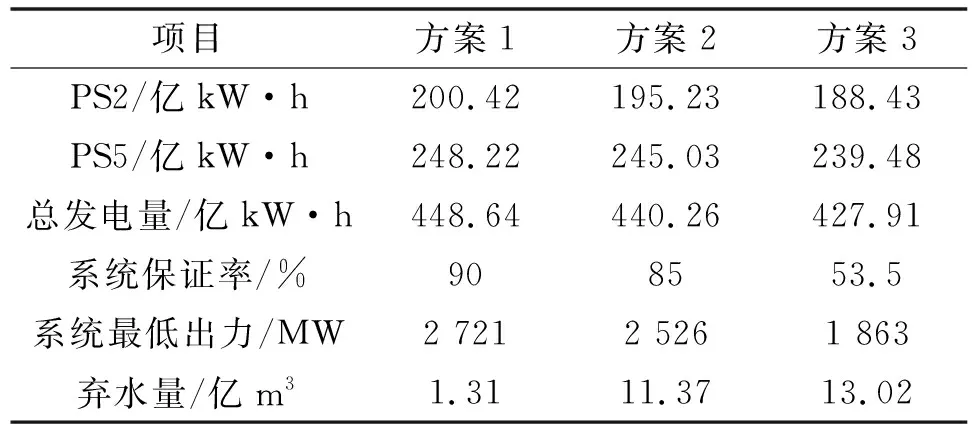
表8 3种调度方案结果对比
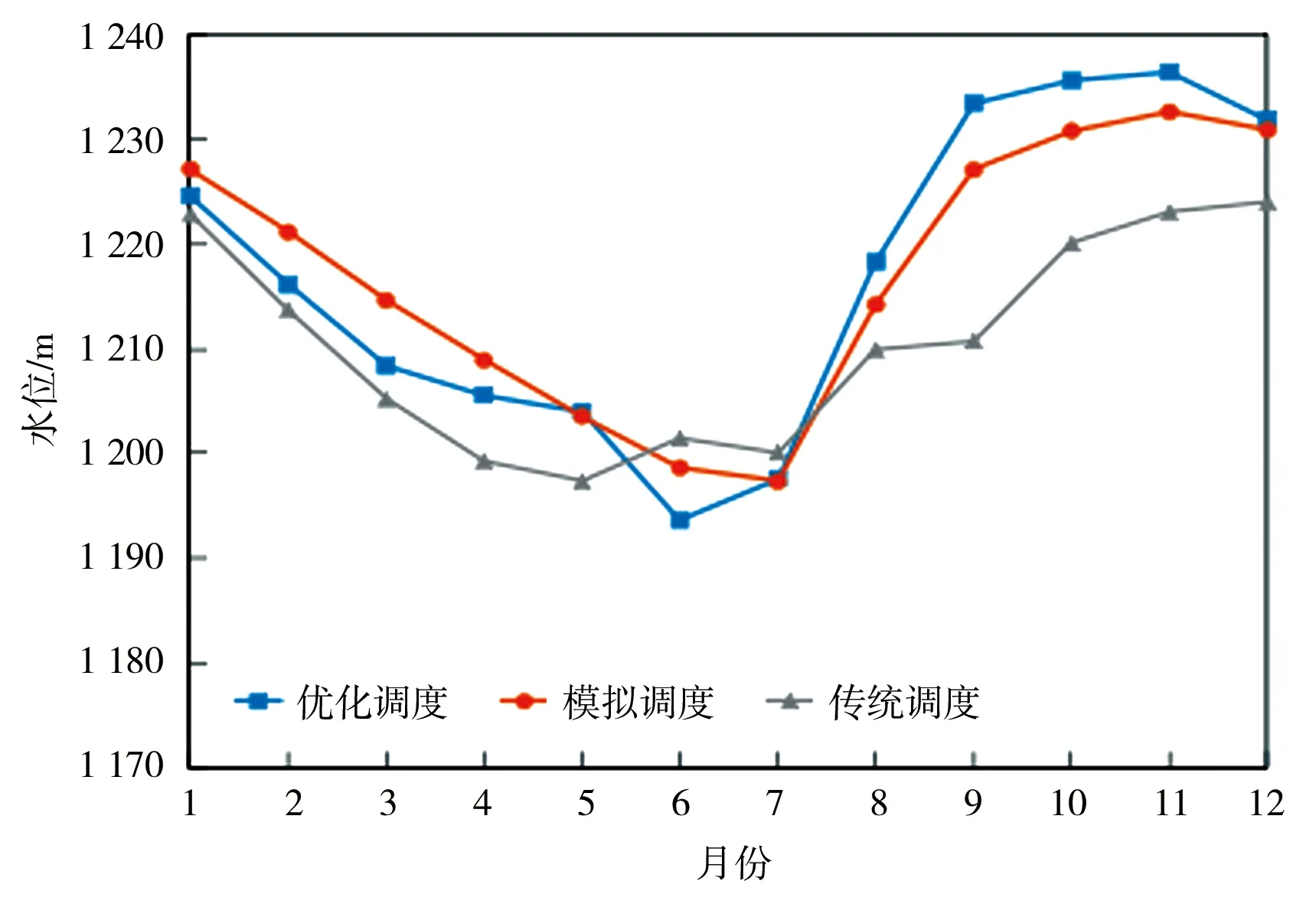
a)PS2水位变化过程
从图4a、4c可以看出PS2、PS5在优化调度和模拟调度中枯期的水位均高于传统调度。这是由于在枯期风、光出力较大,传统调度模式下为了满足发电保证率要求,水库在枯期需要大量放水发电从而导致运行水位较低;而在水风光联合调度时,风光出力较大的枯期水电可以适当地降低出力,从而将平均值维持在高水位运行。
水风光联合调度模型以联合发电量最大为目标,同时考虑了断面限制。为了提高总体发电效益,减少弃水、弃电,水电在汛前尽量降低水位,为汛期充分消纳风、光腾出空间。在汛期来水最大阶段,从图5中1倍风光装机情况下不同年份6、7月出力也可以看出,7月有多次达到了断面上限,因此7月的弃电压力很大。在断面限制条件下,为了避免弃水、弃电,具有良好调节性能的PS2、PS5的水位会快速提升,特别是PS2,充分发挥龙头水库的调蓄作用,在这2个月大幅抬高水位,减少梯级总体出力,从而减少弃水、弃电。对于下游的PS5,为了充分利用梯级间协调作用,同时提高断面利用率和总体发电效益,相应的水位提升不如PS2明显,因此优化调度和模拟调度模式下的PS2在7、8月的初水位会高于传统调度模式,而PS5则可能低于传统调度。
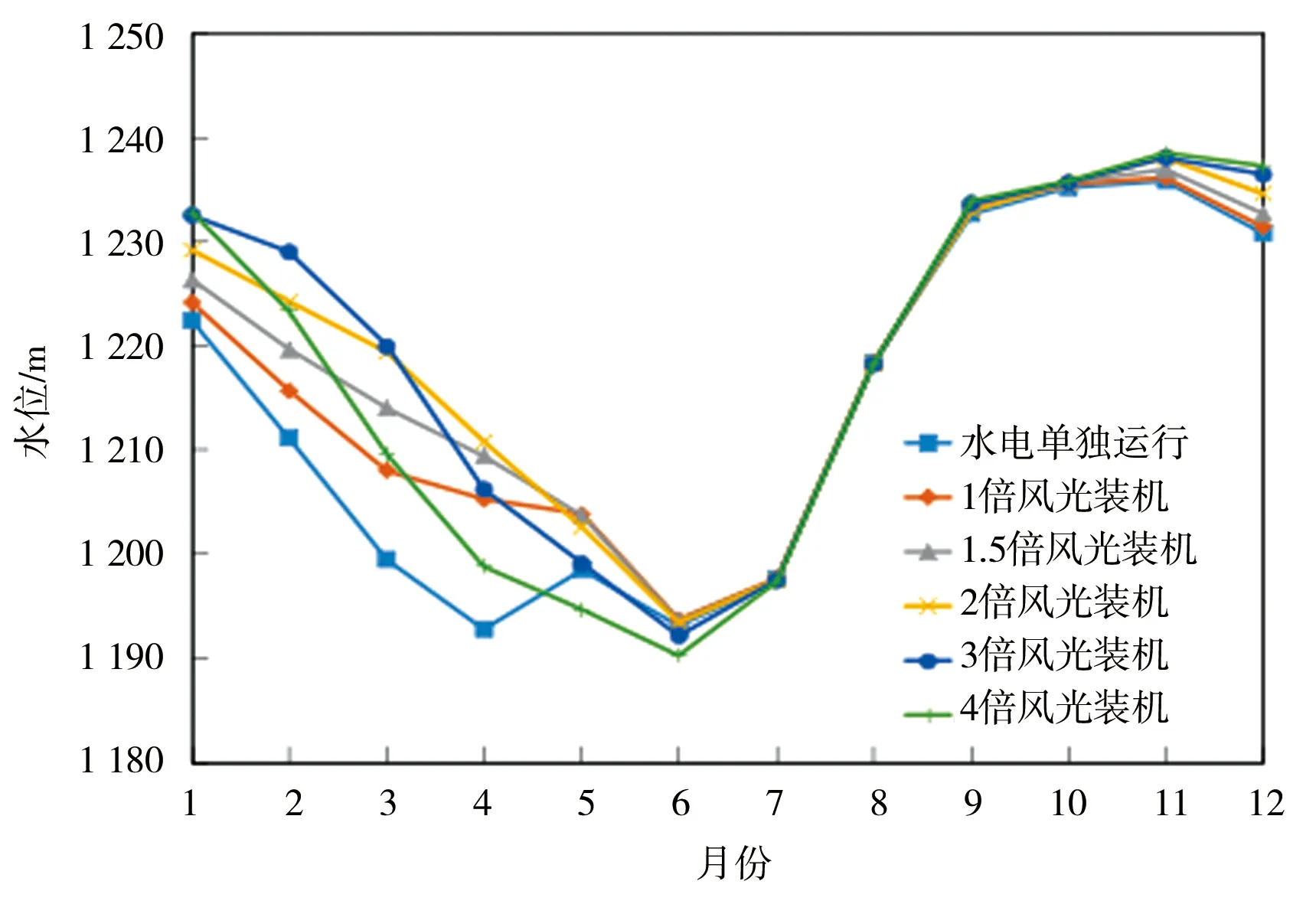
a)PS2

a)6月
从表8可知,传统调度模式下,仅考虑水电的保证出力要求,未考虑水风光系统保证出力要求,在风、光出力较低的时段,仅按照水电保证出力发电时无法满足总体保证出力要求,因此传统调度模式下得到的保证率远低于考虑水风光互补运行模式下的保证率,出力破坏深度也高于互补运行模式下的破坏深度。
总体上,模拟调度方案下的系统总发电量、水位过程以及出力过程均与理想联合调度方案的结果较接近,并且得到的发电量、系统保证率以及最小破坏深度均高于传统调度结果。因此,风光水联合优化调度基础上提取的调度规则,可较好地保证总体发电效益。
为探究6级电站的调度规律和PS2、PS5联合调度的规律是否一致,本文进一步通过6级电站的调度结果进行分析,由于日调节、季调节电站调蓄能力有限,在本次模拟调度中不参与调蓄,因此在PS2和PS5调度结果的基础上进行模拟,具体调度结果见表9。

表9 6级电站多年平均发电情况
从表9可以看出,优化调度模式下的6级电站总发电量最大,多年平均发电量能够达到714.73亿,比模拟调度模式高1.45%,比传统调度模式高3.35%,但是由于日调节和季调节电站调蓄能力有限,虽然通过水风光联合调度,优化调度和模拟调度相较于传统调度在发电效益上确有提升,但是提升程度不如PS2和PS5两个年调节电站大,因此PS2和PS5能够通过水风光联合调度提升发电效益,具有良好的代表性。此外,通过6级电站的调度情况可以看出,本文提取的调度能够较好地满足发电效益,保证率远高于传统调度的61%,且系统发电保证出力要求都要高于3 640 MW(6级电站联合调度下的最低出力要求),因此6级电站调度情况和PS2、PS5联合调度结果相符。
3.5.2风光对调度规则的影响
从3.5.1中可以看出风光能够影响水库的蓄水策略从而影响发电量,因此针对PS2、PS5探讨接入不同规模风光下的水位变化过程。图5a、5b展示了接入“十四五”规划装机(1倍)、1.5、2、3、4倍规划装机还有单独运行水电(不考虑风、光电源)时,通过优化调度模型得到的PS2、PS5的水位过程。从图中可以看出,在接入风光规模0~2倍时,随着风光接入的增加,PS2的水位在11月至次年4月逐渐增抬升,这是因为此时水风光外送通道容量相对充足,在满足系统发电保证率和破坏深度约束的前提条件下,风、光装机越大,出力越大,水电可以相应的减少出力,让水库保持高水位运行来满足发电效益。结合图6,当风光装机达到3~4倍时,水风光系统出力在多年6月皆接近通道上限,因此可以看出水电与风光外送通道竞争激烈,为了减少汛期弃水,水库需要提前消落水位,从图5a、5b也可以看到接入风光装机规模3、4倍时,PS2与PS5在4—6月和枯期的水位相对于1倍风光装机规模都要更低。
此外,通过表10可以看出,系统的多年平均发电量会随着接入风光规模的增加而增加,但是增加幅度逐渐减少,0~1、1~2、2~3、3~4倍多年平均增加电量分别为61.18、60.57、59.36、58.41(亿kW·h)。这是因为随着风光装机的增加,水电与风光外送通道的竞争愈发激烈,弃电量逐渐增加,增加单位风光装机对应的边际效应逐渐减小。因此,也建议在发展风光电站的同时扩大外送通道,避免造成大量弃水弃电。
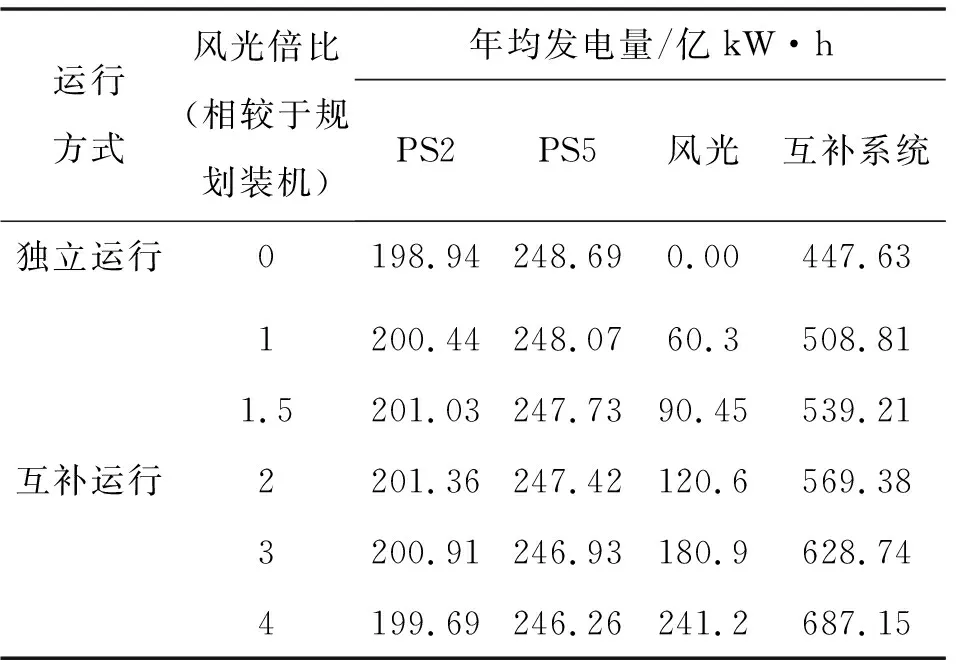
表10 不同倍比风光接入下的多年平均发电量
3.5.3破坏深度和发电保证率对规则的影响
方案1模型中的破坏深度系数为0.6,发电保证率为90%,在方案1的基础上取消这2个约束,采用相同来水及风光数据形成方案5,通过对比2个方案的系统多年平均电量、违反破坏深度约束时段数、满足发电保证出力时段数来探究破坏深度和发电保证率约束对调度规则的影响,具体结果见图7、表11。
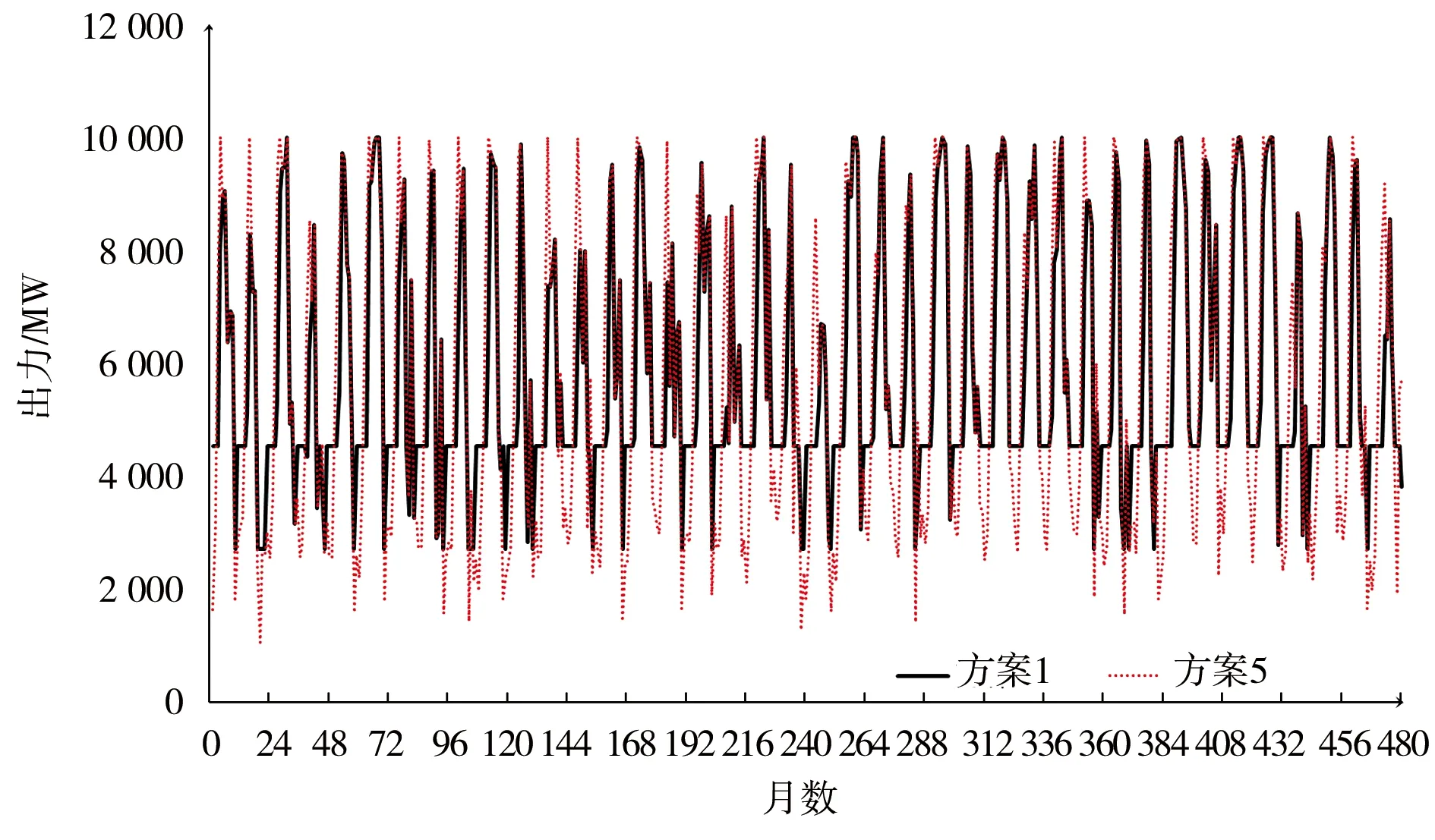
图7 考虑破坏深度和发电保证率约束前后联合调度系统出力
通过图7和表11可以看出,在考虑了破坏深度和发电保证率约束的模型中,得到的系统总发电量略低于不添加的模型,但是并没有出现深度破坏的情况,同时考虑了约束的模型中发电保证率能达到90%,远高于不加约束模型的65%。因此,在水风光联合调度模型中考虑破坏深度和发电保证率能够避免系统出现深度破坏,同时也能满足所规定的发电保证率,保障电网安全稳定运行。
4 结论
本文针对中国风电、光伏大规模并网的能源转型发展形势下,传统水电调度规则难以适用,需要逐步转变为新型电力系统中水风光联合调度情况,提出了考虑发电保证率和出力破坏深度的水风光联合调度规则生成方法,建立了水风光联合调度模型,并通过神经网络提取联合调度规则,基于实例分析得到如下结论。
a)BP神经网络提取调度规则相应的训练集、验证集和测试集R2均大于0.8,MAPE基本都低于10%,模型的拟合准确度较高,可以进一步用来指导模拟调度。
b)通过神经网络提取的水风光联合调度规则得到的年发电量相较于水库常规调度提高2.89%,并且能够满足系统发电保证率和破坏深度要求。
c)在水风光优化调度模型中不考虑破坏深度和发电保证率约束时,虽然多年平均发电量能达到510.63 亿kW·h,略高于所提模型下的508.81 kW·h,但发电保证率和极端破坏深度分别为65%和1 060 MW,远低于所提模型得到的90%和2 721 MW,因此所提模型能够在避免系统出现深度破环、满足发电保证了,并保证发电效益。
综上,所提联合调度规则为风、光大规模并网形势下水风光长期互补调度提供了一种可行途径。未来可以在本文基础上继续开展考虑水风光互补运行条件下风电、光伏容量配置优化等相关研究。

