基于代理模型的广布疲劳损伤平均行为快速确定方法
潘 微,郑旭东,李 杰,李 彦,谈嘉好,陈 昶
(航空工业成都飞机工业(集团)有限责任公司,成都 610092)
在不受外界影响的情况下,机队中50%飞机在所研究的广布疲劳损伤(WFD)敏感结构发生广布疲劳损伤的时间点定义为广布疲劳损伤平均行为[1]。其中,广布疲劳损伤是指在结构相似、应力相当的多个细节部位中同时存在足够尺度和密度的裂纹,随着裂纹的增长,裂纹间的相互影响加剧,从而加快降低结构的剩余强度,使结构不再满足剩余强度要求[2]。基于断裂力学的确定性分析在评估工程设计和安全性、预测结构寿命、对不同类型缺陷的寿命评估等方面一直起着重要的作用,但是由于结构中出现孔洞、位错、夹杂等随机缺陷导致了裂纹萌生及扩展的不确定因素,使疲劳分散性成为材料的固有属性,因此基于疲劳统计学等理论建立裂纹随机萌生和扩展的威布尔分布模型,进而对预测多裂纹结构寿命有着重要的意义。另一方面,确定广布疲劳损伤平均行为求解复杂,需要消耗大量时间,因此基于代理模型的快速求解方法对广布疲劳损伤平均行为工程评估有重要意义。
在确定广布疲劳损伤的概率统计特性研究中,闫晓中等[3]、雷晓欣等[4]针对多部位损伤(MSD)结构,通过蒙特卡洛法模拟,提出多裂纹疲劳损伤随机模型,实现了多裂纹随机萌生和扩展及广布疲劳损伤发生的过程。Ai 等[5]提出基于缺陷的大小和位置来说明制造缺陷对疲劳寿命的影响的概率模型,通过对具有威布尔分布的表面初始裂纹的损伤机理进行建模,得出考虑缺陷表面位置影响的校正因子。
本文在已有的研究基础上,建立裂纹萌生和扩展模型,利用ABAQUS 二次开发得到的应力强度因子数值,根据蒙特卡罗法预测广布疲劳损伤平均行为,在保证精度的情况下预测结构发生概率疲劳时的全寿命。最后,通过机器学习建立广布疲劳损伤仿真程序训练集,使用多项式响应面和高斯过程回归的代理模型进行训练,可以快速确定结构发生广布疲劳损伤时的平均行为。
1 概率疲劳分析方法
1.1 裂纹随机萌生模型
由于材料本身的不均匀性、不同加工方式、试件大小、试验误差及试验环境等因素,会引起结构疲劳寿命的分散,从而在多孔结构中孔边裂纹萌生位置及次序具有随机性,在含有多个相似细节结构中,第i个细节的裂纹萌生寿命Ni(0),i=1,2,…,M由下式给出
式中:Ci、m为材料常数。第i个危险细节的随机参数服从对数正态分布[6],即
式中:C0i为服从标准正态分布的随机参数,下角标0为Ci的初始值和SlgCi分别为Ci的对数均值和对数标准差。
1.2 裂纹随机扩展模型
Paris 裂纹扩展公式计算过程简便,便于运用于工程上的具体运算,Paris 裂纹扩展公式为
式中:G、n为裂纹体的材料特性常数;△K为应力强度因子幅值,即△K=Kmax-Kmin。
裂纹扩展的分散性表现为将材料特性参数G用随机变量Gi表示,即
三参数正态分布可以更好地表示随机参数的可变性,引入变量ui,其表达式为
ui的概率密度函数满足三参数对数正态分布[7],如下式
式中:τ 为位置参数;α 为分散参数;β 为形状参数,通过试验数据可以得到。根据三参数正态分布的性质,Gi可以通过下式得到,即
式中:G0i为服从标准正态分布的随机数,由随机发生器产生。
2 广布疲劳损伤平均行为分析实例
结构的全寿命Nf为裂纹萌生寿命N和裂纹扩展寿命Nc之和,即
由第1 节提出的裂纹概率萌生模型,应用蒙特卡罗法,得到结构的裂纹萌生寿命;通过ABAQUS 建立七孔板裂纹尖端应力强度因子计算模型,七孔板的有限元模型如图1 所示。

图1 七孔平板FEM 模型
通过ABAQUS 二次开发获得裂纹扩展每个增量步的裂纹尖端应力强度因子,建立裂纹扩展的概率模型,最后得到整个结构的全寿命。具体步骤如下。
第一步,由蒙特卡罗法得到M个孔边危险细节的萌生寿命Ni(i=1,2,…,M-1,M)。
第二步,按照裂纹萌生顺序依次给每个危险细节以最小可检裂纹尺寸为1.27 mm 的初始裂纹。
第三步,由组合法求解应力强度因子,计算复杂边界条件下每个孔边裂纹的应力强度因子。
第四步,根据裂纹扩展随机模型计算出裂纹扩展增量,由塑性连通准则和Kc断裂准则共同判断结构是否失效,若没有失效,则继续重复以上计算;若失效,本次模拟失效。
为验证方法的准确性,本文以七孔板为例进行寿命预测,根据文献[8]试验数据,概率模拟过程中的疲劳载荷最大值分别为Pmax=82 kN,Pmax=90 kN,Pmax=98 kN,应力比均为0.1,材料为LY12-CZ 铝合金,材料参数见表1,裂纹随机萌生、扩展参数见表2 和表3。

表1 LY12-CZ 铝合金材料参数

表2 LY12-CZ 铝合金裂纹随机萌生参数

表3 LY12-CZ 铝合金裂纹随机扩展参数
在3 种应力水平下,分别进行100 次蒙特卡罗模拟抽样,模拟结果分别如图2—图4 所示。

图2 Pmax=82 kN 寿命累计分布曲线

图3 Pmax=90 kN 寿命累计分布曲线

图4 Pmax=98 kN 寿命累计分布曲线
从图2—图4 中可以看出,在不同载荷作用下七孔板结构的WFD 失效时刻累计分布曲线,并且可以得到50%概率下的广布疲劳损伤敏感结构疲劳循环数,即广布疲劳损伤平均行为分别为Nave,82=230 450 次、Nave,90=164 665 次、Nave,98=121 700 次。平均行为计算结果与试验结果对比见表4,其中为对数寿命的平均值为试验对数寿命的平均值;SlgNc为对数寿命的标准差,SlgNt为试验对数寿命的标准差。

表4 七孔板计算结果与试验结果对比
从表4 中可以看出,MSD 结构广布疲劳平均行为模拟结果与试验误差仅在6%之内。
3 基于代理模型的快速分析方法
为了继续节约计算成本,可以采用机械设计与机器学习领域中的代理模型方法。
代理模型的基本思想为将复杂的仿真程序看作“黑箱”,使用合适的试验设计方法得到抽样矩阵,抽样矩阵的每一组设计变量的值为一个输入向量。将抽样矩阵输入到仿真程序中获取与之对应的一次随机失效寿命值,建立抽样点-程序响应值间的对应关系作为代理模型的训练集,对选定的代理模型进行训练以得到拟合或插值关系。建立代理模型的步骤如下。
第一步,确定设计变量及变量空间。
第二步,选取合适的试验设计技术(DOE),获得设计变量的抽样矩阵。
第三步,执行仿真程序,获得输入样本点对应的输出响应。
第四步,选取合适的代理模型,建立代理关系,通过训练集对代理模型进行训练。
第五步,精度校核。
为避免过多地输入维度,需对输入参数进行筛选。首先确定代理模型中的设计变量,选取应力水平S、裂纹随机萌生参数m、裂纹随机扩展参数n三个参数为设计变量。其次需要确定3 个参数的变量空间,参数m、n服从正态分布,理论上的变量空间应该是(-∞,+∞),一般情况下选取变量空间为[μ-5σ,μ+5σ],其中μ 为均值,σ 为标准差。应力水平根据工程实际选择变量空间。见表5。
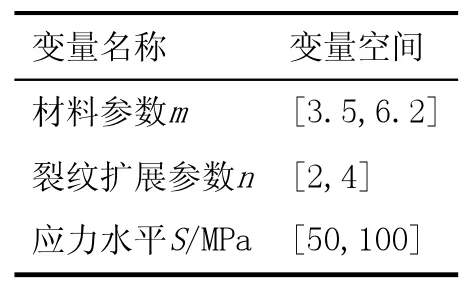
表5 设计变量的变量空间
本文选取拉丁超立方法获得设计变量的抽样矩阵,建立了50 个样本点,在仿真程序中使用蒙特卡罗法抽样50 次获得平均行为作为输出响应,建立多项式响应面法代理模型,由输入-输出响应作为训练集训练代理模型。
基于高斯过程回归模型和多项式响应面模型(RSM)分别训练训练集,通过交叉验证方法进行机器学习验证,验证精度指标见表6。
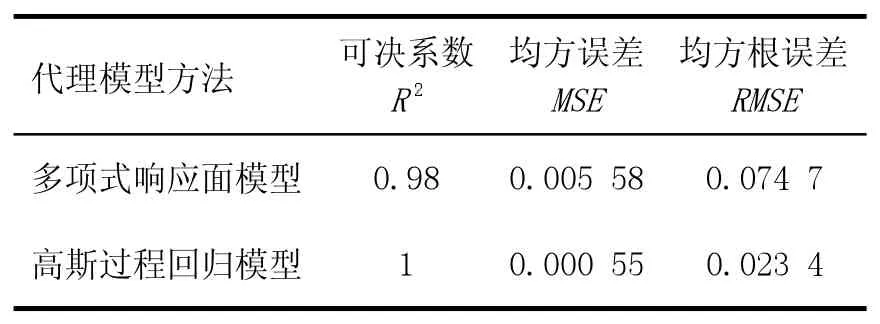
表6 模型学习验证指标
由表6 可以看出高斯过程回归模型精度更高,拟合效果也很好,高斯过程回归模型响应结果如图5 所示。建立测试集,由测试数据对高斯过程回归模型进行测试验证,验证结果显示误差不超过10%,且节约了大量的时间计算成本。
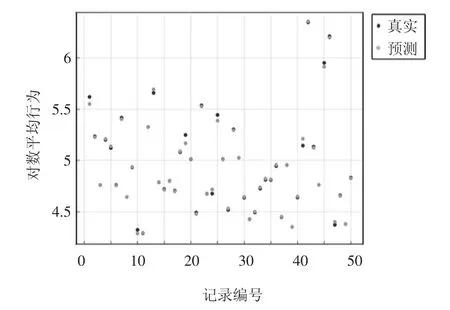
图5 高斯过程回归模型响应图
4 结束语
本文建立了裂纹随机萌生和扩展模型,利用ABAQUS 二次开发得到的应力强度因子数值,根据蒙特卡罗法预测广布疲劳损伤平均行为,广布疲劳损伤平均行为与试验对比误差在6%之内;通过建立代理模型的方式,建立训练集和平均行为输出响应对高斯过程回归模型和多项式响应面模型进行训练学习,由测试数据对模型进行验证显示,高斯过程回归模型精度更高,训练后的预测效果误差不超过10%,并且可以节约90%的计算时间成本,所构建的高斯过程回归模型可以精确地确定广布疲劳损伤平均行为。

