多层尺寸梯度面心立方点阵结构力学性能研究

张武昆,谭永华,高玉闪,王珺,赵剑

(1. 西安航天动力研究所液体火箭发动机技术重点实验室,710100,西安; 2. 航天推进技术研究院,710100,西安)

点阵结构具有高比刚度和高比强度等诸多优异的力学性能[1-2],同时内部巨大的开放式空隙也使其具有良好的抗冲击吸能和对流换热等多功能性能[3-4],目前已经应用于航空航天[5-7]、车辆、医学等诸多领域。近年来,在均匀点阵结构的基础上,通过改变相对密度或拓扑结构等方式而形成的梯度点阵结构[2],这种结构具有更优异的力学性能和更高的结构效率。另外,通过材料梯度分步的设计也能够使其更贴近工程实际应用需求和仿生结构形式,因此梯度点阵结构引起了国内外诸多学者的广泛关注。

当前,由于增材制造技术的不断发展[8-9],梯度点阵结构的制备更加方便快捷[10]。梯度点阵结构的形式主要有4种:材料梯度、截面梯度、胞元尺寸梯度和胞元拓扑梯度。其中,关于截面梯度的研究很多。朱凌雪等基于梯度化因子,采用数值方法研究了面板和芯层梯度因子对金字塔点阵结构在平压和爆炸载荷下吸能性能的影响,认为梯度点阵结构的吸能值相比非梯度结构大大增强[11-12]。乔及森等研究了相同质量下梯度率对铝蜂窝夹芯板结构能量吸收的影响[13]。Niknam等研究了多种梯度组成形式的点阵结构的压缩承载能力和能量吸收性能,结果表明,相对密度垂直于外部压缩力方向变化的梯度组成形式最优[14]。Choy等研究了梯度蜂窝结构的性能,认为梯度结构的吸能量和应变呈指数增加关系,而均匀结构则表现出近似的线性关系[15]。

虽然截面梯度点阵结构易于设计且性能相比均匀结构有所增强,但是截面梯度点阵的小截面很容易在承受振动或冲击等载荷下成为薄弱环节,进而造成整体刚度下降、局部疲劳断裂或冲击损伤破坏等失效行为。同时,小截面对制造和工艺的要求更高。胞元尺寸梯度结构不改变截面大小,仅通过改变胞元的边界尺寸来改变相对密度,因此设计更加灵活。Bai等研究了尼龙(PA2000)制备的尺寸梯度体心立方点阵(SG-BCC)的压缩行为和能量吸收性能,认为SG-BCC相比截面梯度体心立方点阵(RG-BCC)具有更好的承载和能量吸收性能[17]。此外,Bai等还通过Ti-6Al-4V制备并比较了均匀体心立方(BCC)、垂向尺寸梯度BCC和横向尺寸梯度BCC点阵结构的力学性能,结果表明:横向尺寸梯度BCC点阵结构的压缩变形模式与均匀结构相似,而垂向尺寸梯度BCC点阵结构的弹性模量和能量吸收分别提高了17.53%和59.43%[17]。然而,上述研究中针对梯度点阵结构等效弹性模量的计算,一种是通过仿真或试验得到单层性能后组集得到,另一种是基于统计的Gibson-Ashby模型预测整体的等效模量,并没有从理论直接给出预测结果,且没有研究不同梯度因子对结构性能的影响规律。

相比于BCC点阵结构,面心立方(FCC)点阵有着更优异的力学性能[18-20]。然而,针对尺寸梯度面心立方点阵结构(SG-FCC)的研究目前还未见公开发表的文献。本文设计并选用316L材料制备了两种FCC点阵结构,通过试验、理论和有限元方法研究了尺寸梯度面心立方点阵结构的力学性能。

1 设计与制备

图1 FCC点阵结构构型Fig.1 FCC lattice structure configuration

考虑增材制造的工艺约束[21](特征尺寸大于0.2 mm、成形质量和力学性能随悬空角的减少而降低、加载方向与打印方向平行时力学性能更强等),保持胞元杆直径不变,设计并制备了均匀FCC(U-FCC)、尺寸梯度FCC(SG-FCC)两种类型的点阵结构,梯度方向为垂直方向,如图2所示。两种点阵结构均为5×5×5胞元,包络尺寸为20 mm×20 mm×20 mm。U-FCC的单胞尺寸为4 mm×4 mm×4 mm,而SG-FCC点阵结构的每层高度比上层少1 mm,胞元杆直径为0.9 mm。点阵结构的相对密度计算式如下

SG-FCC点阵结构 U-FCC点阵结构图2 FCC点阵结构设计Fig.2 FCC lattice structure design

(1)

式中:Vl为点阵结构的实际体积;Ve为点阵结构的等效体积。通过计算机几何模型计算得出,SG-FCC点阵结构每层的相对密度从上到下分别为0.259 1、0.206 7、0.180 4、0.165 7、0.156 8,U-FCC点阵结构相对密度为0.180 4。假设梯度正方向为相对密度从小到大的方向。

采用BLT S310机器打印点阵结构,基材料为不锈钢SS316L,制备技术为选择性激光熔融(SLM)。激光功率为200 W,扫描速度2 m/s,分层厚度50 μm。打印产品如图3所示。

图3 增材制造的试样Fig.3 Samples made by additive manufacturing

2 试验和仿真

2.1 试验

采用美特斯700 kN微机控制电子万能试验机(美特斯工业系统(中国)有限公司)对试验件进行室温环境下的准静态加载实验。为了获得材料性能,采用相同的技术,制备标准哑铃型拉伸试样,试样尺寸根据ASTM E8/E8M-21标准[22],中心考核段长为50 mm,直径为12.5 mm,拉伸速度为0.5 mm/min。材料名义应力、应变曲线如图4所示。材料拉伸弹性模量为205 GPa,屈服强度为571 MPa,拉伸强度为685 MPa,材料密度为7 971 kg/m3,试验结果与Casati等采用SLM技术制备的316L不锈钢材料的测试结果比较接近[23-24]。根据ISO 13314: 2011标准进行压缩试验,设定加载速率为1 mm/min,加载方向为梯度正方向。在对点阵结构进行压缩实验时,采用数码相机记录点阵结构压缩过程中的变形。打印点阵试件的质量比较如表1所示,实测结果与理论结果误差较小,说明打印精度较高。为方便性能比较,设计的两种点阵结构的质量总体相差不大。

表1 点阵试件打印质量

图4 SS316L材料拉伸应力应变曲线Fig.4 Tensile stress-strain curve of SS316L material

2.2 有限元模型

采用ABAQUS 6.14的EXPLICIT模块建立点阵结构有限元模型,并进行准静态压缩仿真研究[25]。根据下式计算真实应力和应变数据

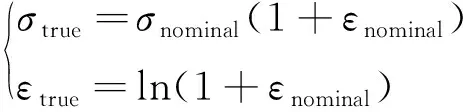
(2)

式中:σtrue和εtrue分别为真实应力和应变;σnominal和εnominal分别为名义应力和应变。

采用Li等关于BCC(体心立方)点阵结构准静态压缩的仿真分析方法[27],用两块刚性平板模拟试验机的两个压头。为了模拟平板与点阵结构之间的接触情况,在切向设置摩擦因数为0.1的摩擦接触,在法向设置硬接触。整体模型采用通用自接触。为保证实验准静态分析的要求和计算精度,减少计算时间,采用质量缩放方法,且保证分析中系统的动能占总能量的比值小于5%。在网格划分方面,采用2节点3D梁单元(B31)。通过网格收敛性分析,设置网格尺寸为0.3 mm。有限元模型如图5所示。其中,Ux、Uy、Uz分别为x、y、z3个方向的位移,Rx、Ry、Rz分别是这3个方向的转角,Vz为z方向的速度,方向向下。

图5 SG-FCC点阵结构有限元模型Fig.5 Finite element model of SG-FCC lattice structures

3 分析与讨论

3.1 压缩过程分析

图6为U-FCC和SG-FCC点阵结构在压缩过程的应力、应变曲线。由图6可以看出,同种结构形式下两个试件的应力、应变曲线基本重合。其变形过程大致分为3个阶段,即线弹性阶段(0<ε<0.02)、塑性平台阶段(0.02<ε<0.55)和致密化阶段(ε>0.55)。不同的应变值下,U-FCC结构和SG-FCC的应力、应变曲线有一定差异。在线弹性阶段基本相似,而塑性平台阶段差异明显,具体表现为SG-FCC点阵结构应力先上升,应力水平明显高于U-FCC点阵结构;然后下降,应力水平略微低于U-FCC点阵结构;然后再上升,应力水平高于U-FCC点阵结构。而U-FCC结构则一直上升,但是不同的应变阶段下应力增长速率不同。在点阵结构压缩后期,两种结构呈现致密化,各层均被压实,压应力迅速增大。此时,力学性能取决于基体材料,故点阵结构的压缩过程仅分析致密化阶段开始前的阶段,即ε<0.55。点阵结构的等效力学性能对比如表2所示。由表2可知,相比U-FCC点阵结构,SG-FCC点阵结构的刚度和比刚度分别增长了6%和4.3%,两者的强度和比强度相差不明显,该结论与Bai等关于尺寸梯度BCC点阵结构强度的研究类似[17-18]。但是,相比U-FCC点阵结构,SG-FCC点阵结构的刚度和比刚度更高,分别增加了17.8%和16.2%。根据Choy等和AL-SAEDI等的研究成果[15, 27],相比于均匀点阵结构,截面梯度形式的点阵会造成刚度和比刚度的大幅减小,这也显示出尺寸梯度相比截面梯度点阵结构在刚度方面的增强优势。

表2 点阵试件结构等效力学性能

数值分析和试验得到的两种点阵结构压缩应力、应变曲线对比如图7所示。结果表明,实验得到的压缩响应曲线与有限元分析得到的曲线在线弹性段和塑性平台段吻合较好,验证了有限元模型的准确性。在致密化阶段,由于杆梁模型难以准确模拟由点阵杆件在大变形压缩后的挤压接触力学行为,因此偏差较大,需要采用实体有限元模型。因致密化阶段并不作为文章的研究重点,本文综合考虑计算效率,可以采用杆梁有限元模型进行分析。

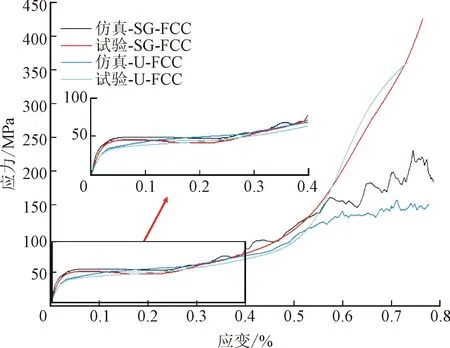
图7 点阵结构试验与有限元模型应力应变曲线对比Fig.7 Comparison of lattice structure stress-strain curves between test and finite element model

图8为SG-FCC和U-FCC点阵结构压缩过程中不同应变水平的变形模式。在压缩起始段,SG-FCC点阵结构相对密度较小的层先产生变形,而相对密度较大的层则变形不明显;相对密度较小的层更高,左右相邻杆件角度更小,相比U-FCC点阵结构在梯度方向的传力效率更好,因此在初期刚度性能好。随着压缩位移的增大,相对密度较小的层相邻杆件角度增大,承载性能下降,这是造成其在塑性平台阶段初期应力水平下降的主要原因。由于相对密度较小的层杆件较长,压缩后致密化结构体积更大,因此结构整体表现为“梯形”现象。最后,各层均逐渐压缩至相互接触,应力水平也逐渐上升,直到结构整体进入致密化,应力急剧增加。U-FCC点阵结构在压缩中表现为上下层先发生大变形,中间层之后发生变形,压缩过程中结构总体表现为两端细中间粗的“椭圆形”现象。Huang等通过对不同杆件角度下金字塔点阵结构的压缩行为研究[29],也得出类似的结论:当点阵结构的杆件角度大于45°时,随着角度的增加,其力学性能会逐渐增强。另外,根据有限元计算的应力云图,SG-FCC相比U-FCC点阵结构的低应力区面积更少,应力梯度更小,也显示出SG-FCC相比U-FCC点阵结构在承载能力和结构效率方面的优势。

相比实体结构,点阵结构具有更优异的能量吸收性能。衡量指标有能量吸收性能Wε(压缩应变为ε时的吸能量)、比能量吸收性能Wsε(单位质量点阵结构在压缩应变为ε时的吸能量),如下所示

(3)

(4)

式中:ρe为点阵结构的等效密度;σ为结构的压缩应力。

两种点阵结构在实验过程中的吸能量和比吸能量对比如图9所示。可以看出,当ε<0.55时,两种结构的吸能量和比吸能量随应变的变化类似,均呈近似线性增长,但梯度点阵结构的吸能性能优于均匀点阵结构。当ε为0.55时,SG-FCC点阵结构的吸能量为36.83 J/cm3,比吸能量为25.27 J/g。U-FCC点阵结构的吸能量为33.23 J/cm3,比吸能量为22.9 J/g。相比于均匀点阵结构,梯度点阵结构的吸能量提高了10.8%,比吸能量提高了10.36%。U-FCC结构和SG-FCC结构的吸能量试验值和仿真值曲线比较接近(应变小于0.6时),也验证了仿真模型的准确性。

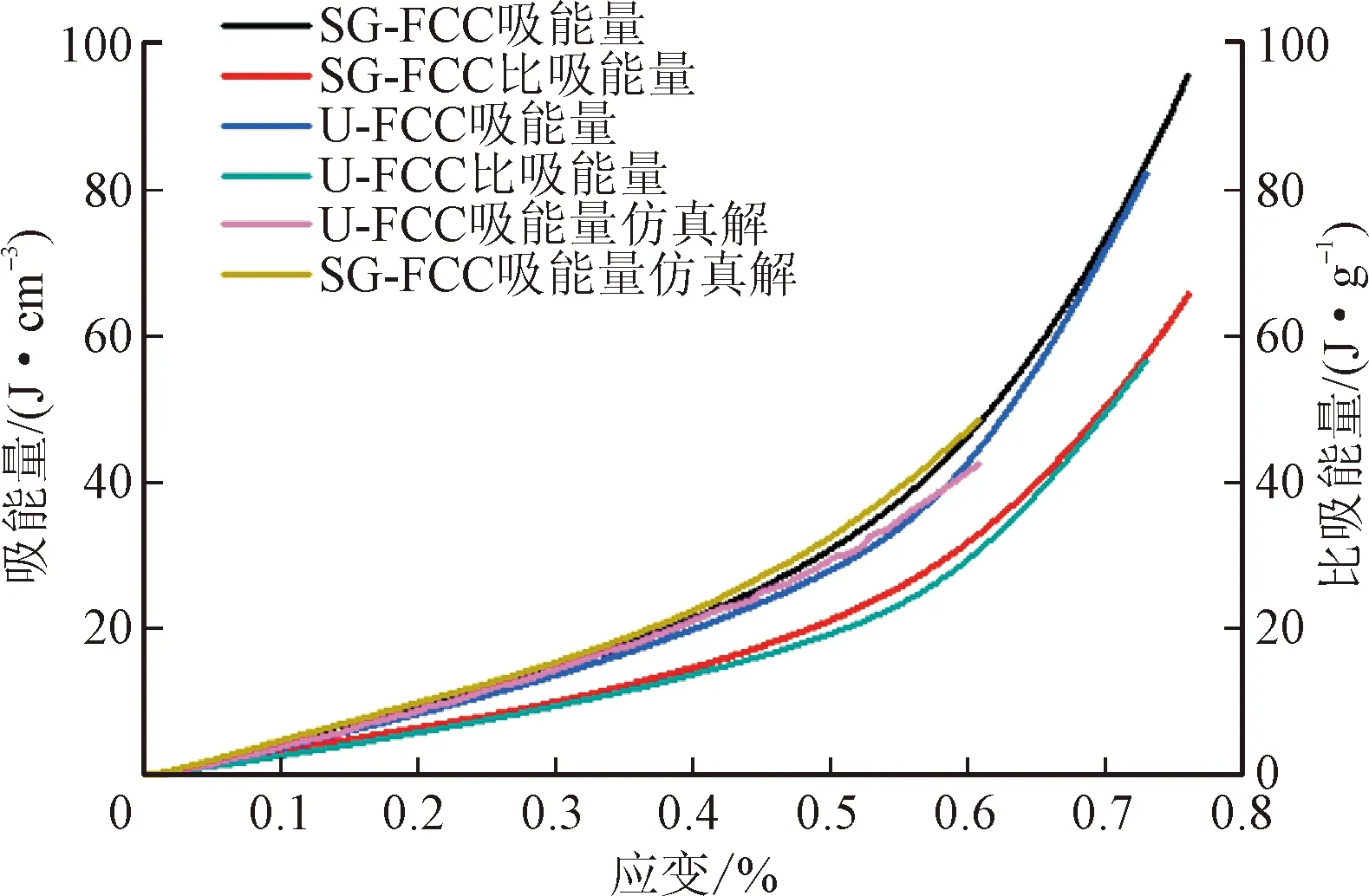
图9 不同点阵结构能量吸收曲线对比Fig.9 Comparison of energy absorption performance curve between different lattice structures

3.2 等效弹性模量模型

由上节可知,试验计算的SG-FCC点阵结构的等效弹性模量为3.032 GPa,U-FCC点阵结构的等效弹性模量为2.574 GPa。梯度点阵结构的等效弹性模量多采用Gibson-Ashby模型预测,本节采用一种基于杆梁变形理论和梯度结构刚度组集方法计算两种点阵结构的等效弹性模量。

由图1中的FCC点阵结构构型可知,可以根据对称性,可以采用图1中的OC杆为例分析受力,如图10所示。将原坐标系xyz旋转得到新坐标系x′y′z′,x′轴沿杆件方向,y′轴沿同平面垂直于杆件方向。根据式(5)中的等效弹性模量方法计算。

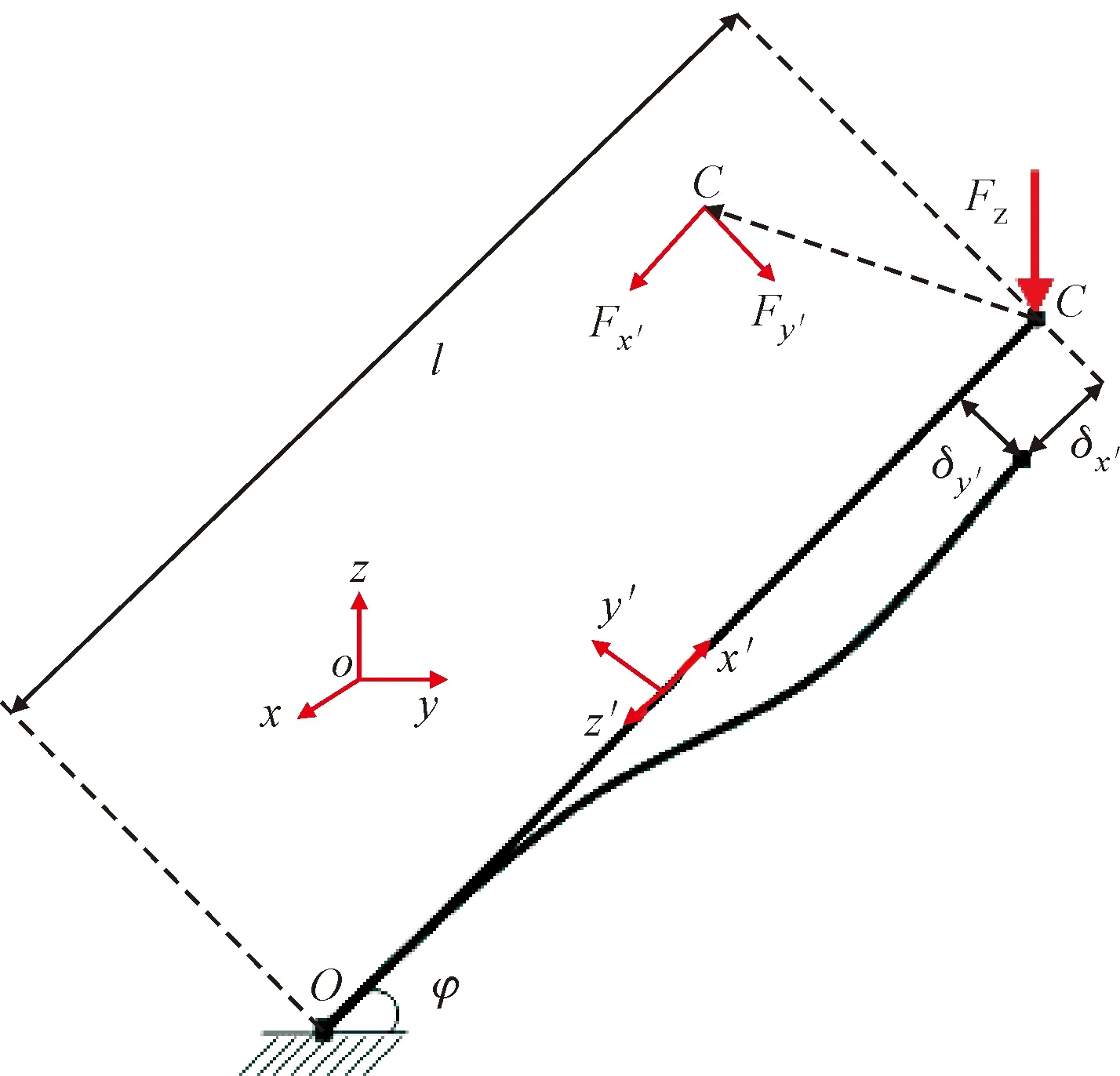
图10 FCC点阵代表性杆件变形模式及受力分析Fig.10 Deformation mode and force analysis of FCC lattice representative rod

(5)

式中:Ez为等效弹性模量;σz和εz分别为等效应力和应变;Fz为z向加载力;δz为z向对应变形。根据矢量运算规则,将Fz和δz分解到x′轴和y′轴,并根据力与位移的关系[30],可得

(6)

(7)

联立式(5)～式(7),可计算出均匀FCC点阵结构的等效弹性模量为

(8)

式(8)为均匀FCC点阵结构的等效弹性模量,当R≤1时,等效弹性模量均可以由此计算。当R>1时,胞元高度增大,杆件的剪切变形作用减弱,在承载后主要呈现弯曲变形特征,因此采用欧拉-伯努利梁理论,将式(7)改为

(9)

联立式(5)、(6)和(9),可计算出等效弹性模量为

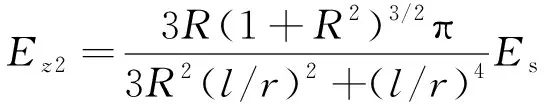
(10)

通过调节R,可以获得不同梯度下FCC点阵结构的等效弹性模量。进而梯度FCC结构整体的弹性模量由不同层的弹性模量叠加计算得到

(11)

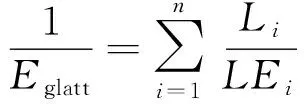
(12)

然而,采用式(12)进行运算时会出现数值误差,不适合进行实际工程计算,可将其改写为

(13)

式中:fk=Lk/L,即单层结构占整体结构的等效体积分数。尺寸梯度点阵结构的相对密度如下

(14)

式中:ρk为第k个单层点阵结构的相对密度。将理论、试验和仿真计算获得的等效弹性模量对比如表3所示。由表3可知,针对U-FCC和SG-FCC点阵结构,理论、试验和仿真计算结果比较接近,验证了提出的梯度点阵结构弹性模量理论模型的准确性。同时也说明了当R>1时,FCC点阵结构杆件的弹性变形更接近欧拉-伯努利梁的弯曲变形模式;当R≤1时,杆件的弹性变形更接近铁木辛柯梁的剪切变形模式。

表3 两种点阵结构弹性模量比较

3.3 梯度因子影响

为研究不同梯度因子下SG-FCC点阵结构的力学性能,设计了不同的梯度因子方案,如表4所示。表4中梯度因子的定义及约束条件如下

表4 梯度化因子研究方案

(15)

(16)

通过设定γi,便可计算出各层的设计高度。采用理论和数值分析方法获得不同梯度因子的点阵结构的力学性能。表5为不同梯度因子点阵结构力学性能对比,图11为不同梯度因子下的FCC点阵结构压缩应力-应变与能量吸收对比。可以看出:对于尺寸梯度FCC点阵结构,不同梯度因子对压缩曲线的变化形状影响不大,与杨等关于不同梯度因子极小曲面点阵结构的压缩研究结论类似[31]。结合上文的压缩过程变形分析,当压缩应变大于0.35时,由于部分杆件提前进入致密段,会造成应力曲线陡增的现象,这是梯度点阵吸能性能得到增强的主要原因。采用梯度化设计后,压缩刚度和能量吸收性能均得到提高。对于刚度性能,当梯度因子为1.5时的等效刚度和比刚度较高,梯度因子为1.963次之,梯度因子为3和2.636的刚度性能比较接近。对于吸能性能(应变0.55),当梯度因子为3时的吸能量和比吸能量较高,梯度因子为1.963和2.636的吸能性能比较接近,且均大于梯度因子为1.5时的性能。当梯度因子为1时的吸能性能和刚度性能均较差。

表5 不同梯度因子点阵结构力学性能对比

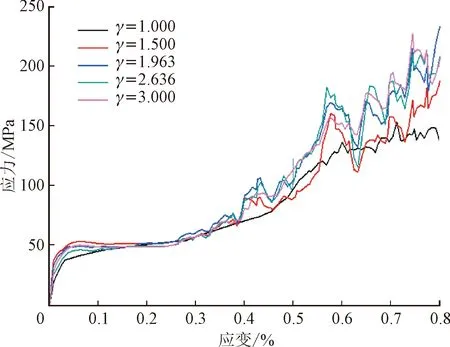
(a)应力-应变曲线

(b)单位体积能量吸收曲线

4 结 论

本文通过理论、试验和数值仿真方法,研究了多层均匀面心立方(U-FCC)和尺寸梯度面心立方(SG-FCC)两种点阵结构在准静态压缩载荷下的力学性能,结论如下。

(1)相比于U-FCC点阵结构,SG-FCC点阵结构的力学性能更加优异,其刚度和比刚度分别增长了17.8%和16.2%,吸能量和比吸能量分别提高了10.8%和10.36%。

(2)基于杆梁变形理论和梯度结构刚度组集方法,针对SG-FCC和U-FCC两种点阵结构,提出了等效弹性模量理论模型计算方法,有限元和试验验证了等效弹性模量理论模型的准确性。

(3)不同的梯度因子下,梯度FCC点阵结构的等效刚度、比刚度、吸能量和比吸能量均不同。当梯度因子为1.5时,等效刚度和比刚度性能较好,当梯度因子为3时,吸能量和比吸能量较好。