数学教学中从几何空间创新理解向量数量积

胡 乙

(江苏经贸职业技术学院,江苏 南京 211168)

在数学中,向量数量积(内积或点积)指:两个向量a和b的模与它们夹角余弦的乘积[1].向量夹角与数量积教学一直是向量教学的重点与难点.在教学实践中,如何引导学生完整准确地理解以上概念,中外学界对此一直未达成共识.

目前国内教材普遍运用物理学中恒力F做功的公式说明向量数量积概念,而从数学几何出发讲授向量数量积,其研究尚处于萌芽状态.程仕然认为从物理学恒力F做功公式推导向量数量积公式有以下不足:一是学生尚不完全熟悉物理做功公式,二是物理学公式与数学公式描述的符号及说法上有不同,可能造成学生新的困扰[2].据此,教师如果转换思路,从求解向量夹角入手推导向量数量积公式,则可能弥补以上不足.陈文雅、江一鸣主张:将向量视为线段,从线段投影出发,运用数形结合思想,将向量数量积视为向量间投影[3].可见,若从几何空间出发设计向量相关教学,则师生教学可能更为轻松.

国外学界倾向于从几何空间出发,首先从笛卡尔坐标定义向量数量积,再运用向量封闭回路法构造直角三角形证明向量数量积公式.如卡尔·P.西蒙等提出应在几何空间中运用封闭回路构造直角三角形,并运用勾股定理推导向量数量积公式[4].此观点已经涉及向量数量积的数学本质,但不完整.完整的向量数量积教学应包含两方面,即从向量坐标法与向量封闭回路法出发,全面讲授向量数量积概念.

此外,通过调整相关概念教学顺序,可能会提高教学效率.按观察问题、解决问题的逻辑顺序,学生应首先认识向量夹角,在计算向量夹角大小的过程中,教师可引导学生归纳出求解向量夹角余弦值的算法,对算法做适当变换后,再引导学生学习向量数量积概念.以上教学设计不仅有利于学生深入理解向量数量积的数学本质,而且可培养学生在解决实际问题中进行数学抽象的能力.

据此,研究拟从数学几何出发,首先引导学生发现笛卡尔平面中的向量夹角,并从向量坐标法与向量封闭回路法两种角度引导学生求解向量夹角余弦值,在此过程中,启发学生归纳出求解向量夹角余弦值的公式,对公式做适当变换后,教师可正式提出向量数量积概念.同时,因为向量是沟通几何与代数的桥梁,为使学生深入理解以上概念,研究将从向量坐标与封闭回路两个角度,引导学生运用向量数量积公式,创新证明欧氏几何直角三角形相关定理,使学生从多角度深入认识向量的概念与作用,并学会在数学、物理学、经济学等不同学科中,主动运用以上知识分析相关数学模型,以此激发学生的学习兴趣,实现教学初衷.

1 向量夹角与向量数量积

与传统教学不同,教师可在笛卡尔平面建立向量夹角,请学生运用三角函数计算该夹角的余弦值,在此过程中,引导学生推导向量数量积公式.待学生熟练掌握后,教师可从向量封闭回路角度再次引导学生理解向量夹角与向量数量积.

1.1 从向量坐标法理解向量夹角与向量数量积

图1 从向量数对(坐标)出发理解向量夹角与向量数量积

cos∠AOB=cos(∠AOX-∠BOX)

=cos∠AOXcos∠BOX+sin∠AOXsin∠BOX

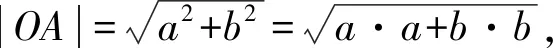
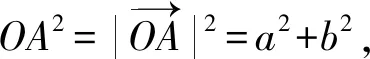
从几何空间出发求解向量夹角时,当学生将两向量起点均平移至原点后,则可通过两向量终点坐标求解向量夹角余弦值,从以上计算过程中定义向量数量积,则学生可能更为容易接受,且更能体会到向量的数学本质.

1.2 从封闭回路理解向量夹角与向量数量积

图2 从封闭回路法出发理解向量夹角与向量数量积

又根据勾股定理,

联立以上三式,展开得:

整理得:

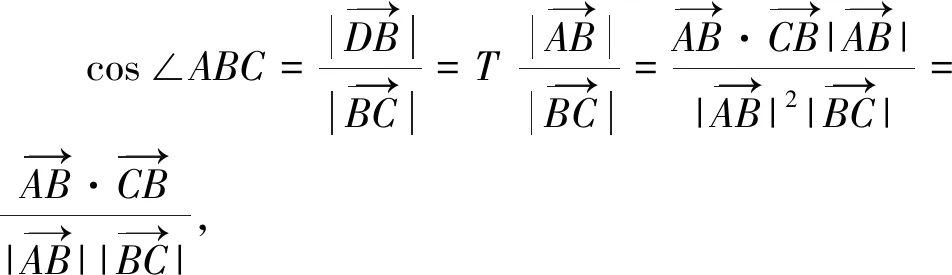
据此,教师可总结向量夹角cosθ的重要性质:当θ为锐角时,cosθ>0;为钝角时,cosθ<0;为直角时,cosθ=0;为零度时,cosθ=1.综上,一般情况下,-1≤cosθ≤1.特别的,当需要证明直线或者线段间夹角为直角时,除了运用综合证明方法外,学生可尝试运用向量数量积求证.此外,在欧氏几何教学中,教师可引导学生尝试运用向量求解相关试题.例如:如果不在同一平面的两线段向量数量积为零,则学生可证明其相互垂直等.学生运用向量求解几何问题,在一定程度上可避免背诵繁琐的定理,同时在解题时可不加或少加辅助线,如此则有利于减轻学生学习负担,激发学生学习兴趣.

2 向量数量积与欧氏直角三角形相关定理的证明

张景中主张运用向量数量积求解或者求证度量几何中垂直、角度值、异面线段长度比值等难题[5].依据试题条件,教师可引导学生从向量坐标法与向量封闭回路法求解相关几何试题.以直角三角形相关定理证明为例,相较于综合证明方法,向量数量积方法则更加简洁高效.

1.3 向量数量积与勾股定理

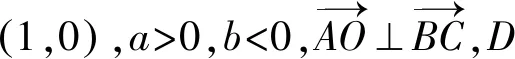
图3 笛卡尔平面中直角三角形的高与中线

a2=-b,b<0,

故AB2+AC2=BC2.

从向量封闭回路法出发,省略繁琐的坐标,学生运用向量数量积公式可直接得到勾股定理.

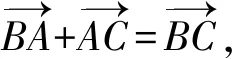
AB2+AC2=BC2.

同理,学生可从向量坐标法证明勾股定理逆定理:

如图3,A点坐标(0,a),B点坐标(b,0),C点坐标(1,0),a>0,b<0,设AB2+AC2=BC2,求证∠BAC为直角.

则b2+a2+a2+1=1+b2-2b,

得a2=-b,a>0,b<0,

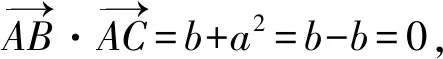
故∠BAC为直角.

与向量坐标法不同,学生运用向量封闭回路证明勾股定理、余弦定理等则更为简洁自然,且几乎不用添加辅助线或构造图形,教师可运用三角形封闭回路性质,再次展示如何证明余弦定理与勾股定理逆定理.

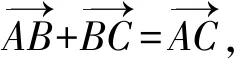
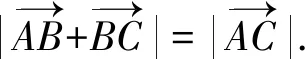
因为结论涉及平方,故对等式两边平方,并运用数量积公式可推理得到等式 :

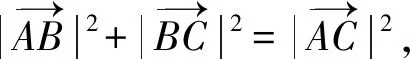
教师仅仅运用向量封闭回路、全程未添加辅助线即完成证明.据此,教师可尝试引导学生用向量知识重新证明几何、代数中相关定理,为学生学习提供新思路,并在此过程中加深学生对向量的理解.

1.4 向量数量积与直角三角形射影定理

用向量证明直角三角形射影定理将更为简洁,如图3,直角ΔBAC中,AO⊥BC,请学生证明:AB2=BO·BC,AC2=CO·CB,AO2=BO·OC.

运用原有坐标,学生可构造如下向量:

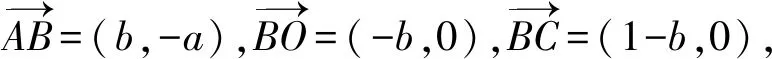
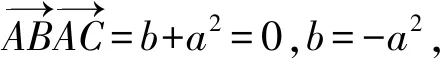
以图3为例,学生可运用向量封闭回路法再次证明直角三角形射影定理.证明的关键是,学生能将已知向量分解为合适的封闭向量,并能运用数量积为零的条件消除无关向量.

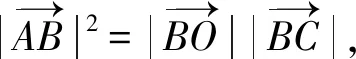
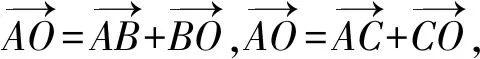
2 总结

从数学几何出发,教师可首先指导学生计算向量间夹角数值,在此过程中,引导学生推导向量数量积公式.教师应从向量坐标法与向量封闭回路法两种角度完整讲授向量夹角与向量数量积.运用向量数量积,学生可创新证明欧式几何中相关定理.限于篇幅,本研究并未详细阐述向量数量积在立体几何、解析几何、不等式等教学内容中的应用.未来教学中,教师可尝试运用质点几何法讲授向量数量积及相关向量知识.