采用神经网络方法建立单摇并步跳绳的能量消耗预测模型研究

李宇轩 陈演 杨俊超 车开萱 邱俊强，2

1 北京体育大学运动人体科学学院，运动生物化学教研室（北京 100084）

2 运动营养北京市高等学校工程研究中心（北京 100084）

跳绳作为一项简单易学且场地需求小的体育运动，在我国校园体育和体能训练等领域均有广泛应用[1]。目前常见的跳绳类型包括单摇、双摇及花式跳绳等[2]，单摇跳绳又可根据不同落地形式分为双脚并步跳和轮换跳，其中在大众健身领域主要以双脚并步跳的锻炼形式为主[3]。同时已有多项研究证实规律的跳绳锻炼能够有效提高锻炼者的心肺耐力、爆发力及协调能力[4]，因此，跳绳运动在全民健身中具有极大的推广潜力。但目前国内现有研究大多集中在跳绳运动的健康效益方面[5]，对于监测跳绳运动能量消耗（energy expenditure，EE）的研究还相对缺乏。间接测热法被认为是测量身体活动能量消耗的金标准[6，7]，但在实际应用中却受限于场地、操作人员及测试成本等因素，并不适用于大样本测试。可穿戴设备的出现，如加速度计、心率表等，相较于气体代谢仪具有操作简便、测试成本低的优势，已在不同人群身体活动监测中得到了广泛应用[8-10]。

加速度计能够采集各运动轴的原始数据（使用count值计数），并代入已验证公式进行能耗计算，但由于现有算法多以走、跑等常见运动模式和日常身体活动为基准[11]，其在应用于监测跳绳等特定运动能耗时常出现较大误差[12-14]，因此在使用加速度计预测特定运动的能量消耗时需建立具体项目的能耗预测模型以提高预测准确性[15]。而伴随加速度计监测技术的迅速发展，单独使用加速度计计数建立线性回归模型的传统能耗预测方法已逐渐被两种改进方法所替代[16]，一种方法是通过加速度计联合一个或多个生理指标（如心率或者体温等）建立能耗预测模型。多项研究已经证实，将心率指标作为加速度计能耗预测模型的补偿因子可以大幅提升爬坡、慢跑等专项运动的能耗预测准确性[17，18]。另一种方法则是通过神经网络等机器学习算法降低加速度计测量身体活动能耗的误差[19]。然而，目前上述改进方法对于跳绳运动能耗监测准确性的研究结论尚未明确。

本研究将以间接测热法测得的不同频率单摇并步跳绳运动能量消耗数据为基准，分析不同频率单摇并步跳绳运动的能量消耗特征，计算精准能耗值与各项生理指标、不同部位加速度计（腰部、两侧腕部、两侧踝部）计数的相关性，同时根据不同建模方式建立基于心率联合不同部位加速度计计数的线性回归模型和神经网络模型并验证模型信度，旨在建立精准的单摇并步跳绳能耗预测模型并确定加速度计的最佳佩戴位置，为单摇并步跳绳运动的能耗监测及在全民健身中的推广提供参考依据。

1 对象与方法

1.1 研究对象

本研究共纳入36名北京体育大学普通（非运动专项）在校大学生，其中男女比例为1∶1。受试者均为汉族，年龄18～30 周岁，18.9 kg/m2≤BMI＜24.0 kg/m2，身体健康，无重大疾病史或家族遗传病史，且基线运动测试达标（即具备1分钟内单摇并步跳绳120次以上的运动能力）。正式实验开始前，受试者需避免参加剧烈运动，无感冒发烧等症状；未服用任何药物；未摄入咖啡因；女性需避免在生理期进行测试。受试者均为自愿参加实验，并签署《知情同意书》。受试者基本信息见表1。

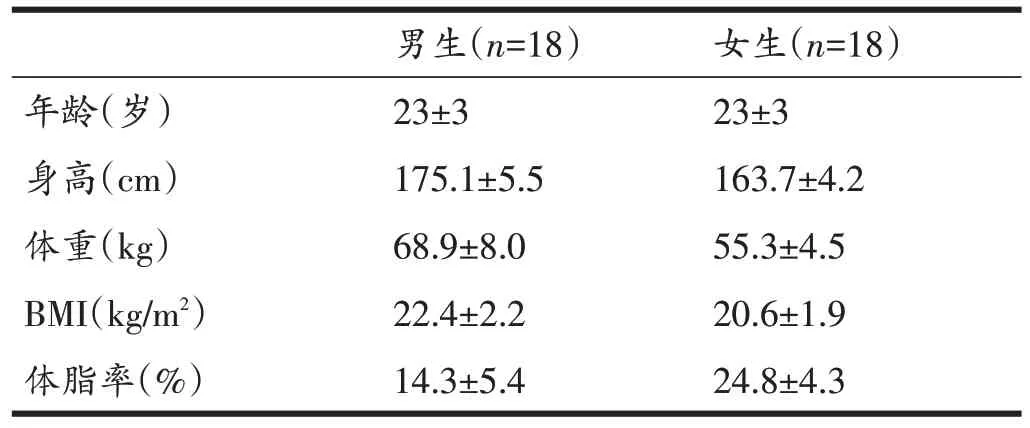
表1 受试者基本情况

1.2 研究方法

1.2.1 实验流程

实验测试由1 次基线测试和3 次不同频率单摇并步跳绳测试组成。需先对受试者进行基础信息采集（身高、体成分测试），然后佩戴便携式气体代谢仪、心率带和加速度计（加速度计佩戴位置为腰部、两侧腕部和两侧踝部），随后完成基线运动测试，低、中、高频率单摇并步跳绳测试。测试时间为2020 年9～10 月，测试场地为北京体育大学科研中心实验室，整个测试期间室内温度湿度均保持稳定，温度为24.7℃± 1.0℃；湿度为61.0%±3.1%。

测试开始前，需让受试者保持安静，待所有测试指标稳定后开始实验，记录运动前5～10 分钟静息状态气体代谢数据，随后开展基线测试和不同频率3 分钟单摇并步跳绳运动测试。整个实验需在3 天内完成，除基线测试外，令受试者随机开展低、中、高频率跳绳测试。具体测试流程如下：

（1）基线测试：受试者进行60 秒尽力单摇并步跳绳，记录整个运动过程中气体代谢仪、加速度计、心率数据、实际跳绳及断绳次数。若基线测试未达标，则不再进行后续跳绳运动测试。

（2）低、中、高频率单摇并步跳绳测试：待受试者基线测试后休息至安静状态，分别进行低、中、高频率（60次/分、100次/分、130次/分）3分钟单摇并步跳绳测试，各频率跳绳测试完成后需休息至静息水平（运动测试后的静息时间不短于15 分钟），方可开展下一次跳绳测试。受试者按照节拍器节奏跳绳，若出现断绳，则需要求受试者立即重新开始跳绳。记录整个运动过程中气体代谢仪、加速度计、心率数据、实际跳绳及断绳次数。若断绳次数大于5次或每分钟平均跳绳次数未能达到对应频率的最低要求，则数据不予纳入。

1.2.2 测试仪器与指标

采用Inbody230 体成分分析仪（韩国）测量受试者体重及体成分；采用CORTEX MetaMax 3B-R2（德国）测试受试者每分钟能量消耗、摄氧量、呼吸商等指标；采用Polar V800 心率带采集受试者心率数据，记录不同频率单摇并步跳绳运动期间的平均心率（HR），计算心率差（ΔHR=运动中平均HR-安静HR）；采用Acti-Graph-GT3X+加速度计记录运动期间矢状轴、冠状轴、垂直轴和三轴向量幅值（vector magnitude，VM）的加速度计计数。

1.3 数据处理与统计

1.3.1 数据处理

采用Excel 2018对受试者基本信息及实验测试数据进行处理，均使用平均值±标准差（±s）进行描述。运动中心率及加速度数据需取跳绳测试后2分钟平稳状态数据，进行能耗特征分析及建立运动能耗预测模型[13]；运动中总能量消耗数据（total energy expenditure，EEtotal）为3分钟跳绳运动净能量消耗（energy expenditure of rope skipping，EERS）与运动后15分钟过量氧耗（exercise post oxygen consumption，EPOC）期间的净能量消耗（energy expenditure of exercise post oxygen consumption，EEEPOC）之和，运动中每分钟能量消耗速率（Rate of energy expenditure per minute during exercise，EEmin）由运动中总能量消耗（EEtotal）换算得出；通过矢状轴（Y 轴即1 轴）、冠状轴（X 轴即2 轴）、垂直轴（Z 轴即3 轴）的加速度计计数换算三轴向量幅值（VM） =（Axis12+Axis22+Axis32）1/2的加速度计数（counts/min）。

1.3.2 统计方法

使用SPSS23.0和MATLAB 2016a统计软件进行数据分析。使用单因素方差分析比较不同频率跳绳能耗特征是否存在差异，检验是否存在方差齐性，采用事后检验LSD对不同频率进行多重比较；通过Eta相关系数分析评价性别与运动能耗之间的相关性（男性作为对照组，男性=0；女性=1），通过Pearson 相关系数分析评价各项基础指标、心率、加速度计计数与运动能耗之间的相关性；经随机抽样将28 名受试者（男∶女=1∶1）的数据作为建模组，其余8名受试者（男∶女=1∶1）的数据作为预测模型的验证组，采用SPSS23.0 软件建立不同部位加速度计的线性回归模型，采用MATLAB 2016a软件建立不同部位加速度计的BP（back propagation）神经网络模型，并使用验证组数据进行模型验证，通过计算各模型预测值与实测值之间的相关系数、平均绝对误差（mean absolute error，MAE）、均方根误差（root mean square error，RMSE）和偏差（Bias）进行预测准确性的比较；通过Graphpad Prism 8 软件绘制Bland-Altman 散点图检验各模型预测值与实测值之间的一致性程度；通过SPSS23.0软件进行等效性检验，以判断各模型预测值与实测值之间是否等效，判断标准为：预测值90%置信区间是否落入实测值等效性区间内（X±10%X）[20，21]。定义显著性P＜0.05。

2 结果

2.1 单摇并步跳绳能耗特征

依据间接测热法对不同频率单摇并步跳绳的精准能耗值进行对比，发现受试者在完成不同频率单摇并步跳绳中的HR、ΔHR、EEEPOC以及EEtotal均存在显著性差异（P＜0.05）。其中低频率跳绳运动中各项生理指标均低于中、高频率，低频率跳绳运动总能量消耗值（EEtotal）比中、高频率分别低7.67 kcal（P＜0.01）和4.92 kcal（P=0.024）。从运动能耗组成分析，EEtotal主要由运动中净能耗EERS和运动后过量氧耗期间的净能耗EEEPOC组成，经对比分析发现运动中不同频率单摇并步跳绳的净能耗EERS之间并不存在统计学差异（P=0.96），但不同频率单摇并步跳绳的EEEPOC存在显著差异（P＜0.05），其中低频率跳绳的EEEPOC分别比中、高频率低4.68 kcal和3.09 kcal（P＜0.01）。虽然中、高频率跳绳运动在实际跳绳次数方面存在显著差异（中、高频率跳绳次数分别为91±12次/min和127±10次/min，P＜0.01），但各项生理指标间不存在显著差异，仅表现为中频率跳绳各项生理指标略高于高频率，具体实验结果见表2。

表2 不同频率单摇并步跳绳能耗特征分析

2.2 各指标与能耗数值的相关性

将受试者各项基础指标、HR、ΔHR 及不同佩戴部位加速度计计数与间接测热法所得的精准能耗值EEmin 进行相关分析发现，EEmin 与性别的Eta 相关系数为0.640，Eta平方值η2为0.410（P＜0.01），说明EEmin与性别之间存在相关关系；且根据Eta相关性分析结果发现，不同性别在跳绳运动期间的EEmin存在显著差异，男性的EEmin 显著高于女性（男性vs.女性：16.8±2.6 kcal/min vs.12.9±2.2 kcal/min，F=71.552，P＜0.01）。同时体重、BMI、ΔHR和实际跳绳次数与EEmin也存在相关关系，相关系数分别为0.580、0.423、0.226 和0.190（P＜0.05）。在不同佩戴位置加速度计参数对比中发现，腰部加速度计参数除X 轴计数值外，Y 轴、Z 轴及VM值均与EEmin存在相关关系（P＜0.05），两侧踝部加速度计Y 轴计数值和VM 值与EEmin 也存在相关关系（P＜0.05），而两侧腕部加速度计参数与总能耗值EEmin 均不存在相关关系（P＞0.05），具体相关性分析见表3。

表3 方程自变量与能耗数值相关性

2.3 线性回归模型的建立

将全部建模组受试者低、中、高频率三组数据，代入多元线性回归模型，以间接测热法测得并计算的精准能耗值EEmin 作为因变量，将性别、体重、BMI、ΔHR、跳绳次数以及不同部位加速度计的VM值、X轴、Y 轴、Z 轴计数值作为自变量，采用线性回归方程中的步进法（Stepwise）分别建立心率联合不同部位加速度计计数的能耗预测模型（EELM），具体结果见表4。

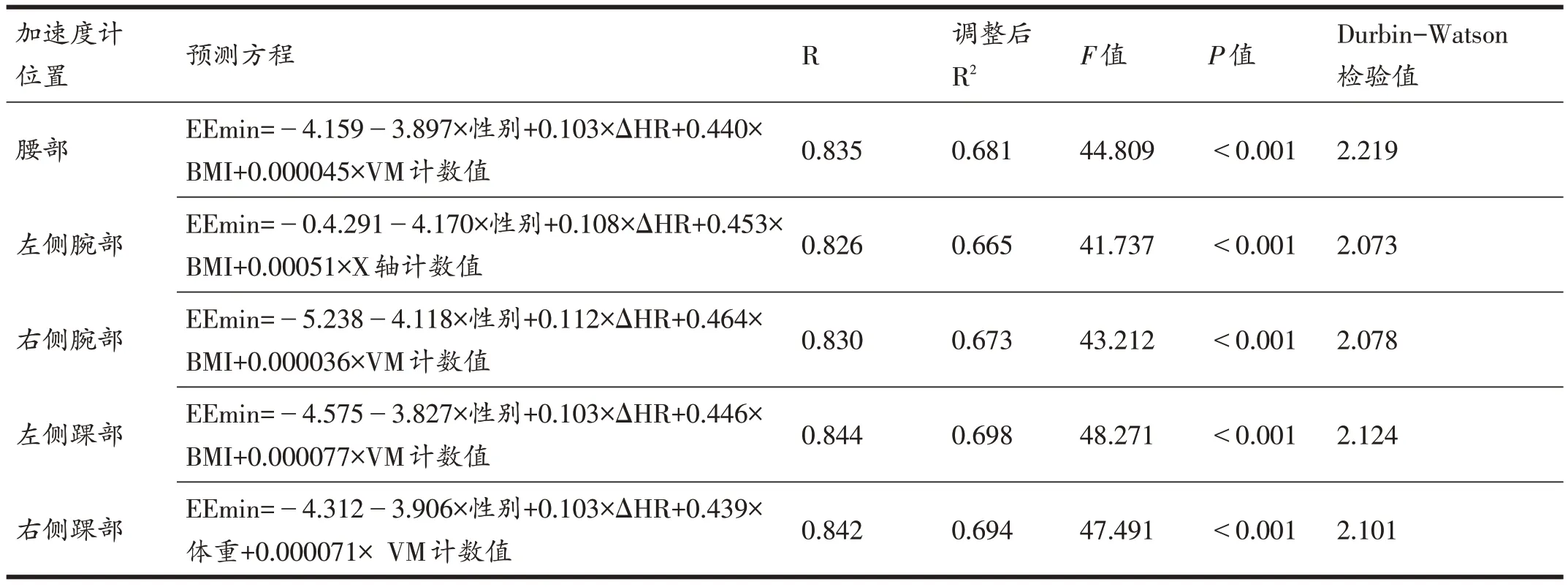
表4 心率联合加速度计线性回归模型

所建立5 个预测模型的调整后R2在0.665～0.698之间，容差值均大于0.1，同时VIF值均小于10，说明预测模型不存在多重共线性。各模型的Durbin-Watson检验值均位于0～4的取值范围内，同时接近于2，表明各自变量间相互独立，不存在自相关。预测模型的F值分别为44.809、41.737、43.212、48.271 和47.491（P＜0.001），说明上述各部位预测模型均具有统计学意义。

2.4 神经网络模型的建立

2.4.1 模型输入层的选取

本研究为了更加直观地对比线性回归模型与神经网络模型之间的预测差异，避免两种模型因自变量选取的不同影响预测结果，选取与线性回归模型相一致的自变量作为神经网络模型的输入层参数，建立心率联合不同部位加速度计的BP神经网络模型（EEANN）。

2.4.2 数据归一化处理

为避免机器学习过程中原始数据值对权值配比的影响，降低迭代次数和训练时长，需对输入层的数据进行归一化处理。采用mapminmax 函数，将所有数值转换至[0，1]区间。

2.4.3 设置网络参数

本研究采用Matlab 软件中的神经网络工具箱（Neural Net Fitting）构建三层BP 神经网络模型，应用工具箱中的newff 函数和LM（Levenberg-Marquardt）算法构建BP 网络并进行模型优化。模型网络参数最终设定初始学习率为0.01，训练目标最小误差为1e-6，最大训练次数为1000，显示训练迭代过程为25。

2.4.4 隐含层节点数目

隐含层节点数目的选取与预测模型的需求、输入层和输出层的单元数目有关。本研究隐含层节点数目采用公式S=（n+m）1/2+a，n为输入层节点数目;m为输出层节点数目；a为1～10的常数。同时采用试凑法，以验证组所得到的平均绝对百分比误差（mean absolute percentage error，MAPE）作为指标，选取MAPE取值最小时的隐含层节点数目。

2.4.5 不同加速度计部位模型的确定

将全部建模组受试者的低、中、高频率三组数据代入BP神经网络模型，通过对模型输入层、输出层、隐含层和网络参数的筛选和调整比较，最终成功建立了心率联合不同加速度计参数的BP神经网络模型，具体结果见表5。

表5 心率联合加速度计神经网络模型

2.5 跳绳能耗预测模型的拟合效果

为了验证各预测模型的拟合效果，将剩余8 名受试者（24组数据）的相关指标回代入各预测模型并与间接测热法所得到的实测值进行比较，具体结果见表6。从模型的整体预测结果来看，各加速度计所建立的线性回归模型预测值与实测值之间的相关性为0.657～0.695，而神经网络模型的预测值与实测值的相关性为0.698～0.780，同时各部位加速度计建立的神经网络模型在MAE、RMSE 和Bias 均低于线性回归模型，说明各加速度计部位建立的神经网络模型预测效果均优于线性回归模型。在对比不同加速度计位置所建立的预测模型时发现，无论是线性回归模型还是神经网络模型，依据腰部加速度计建立预测模型的预测值与实测值的相关性均最高分别为0.695和0.780，同时MAE、RMSE、Bias 也低于其他加速度计部位所建模型，说明依据腰部加速度计参数所建立的预测模型对于跳绳运动能量消耗的预测效果最佳。

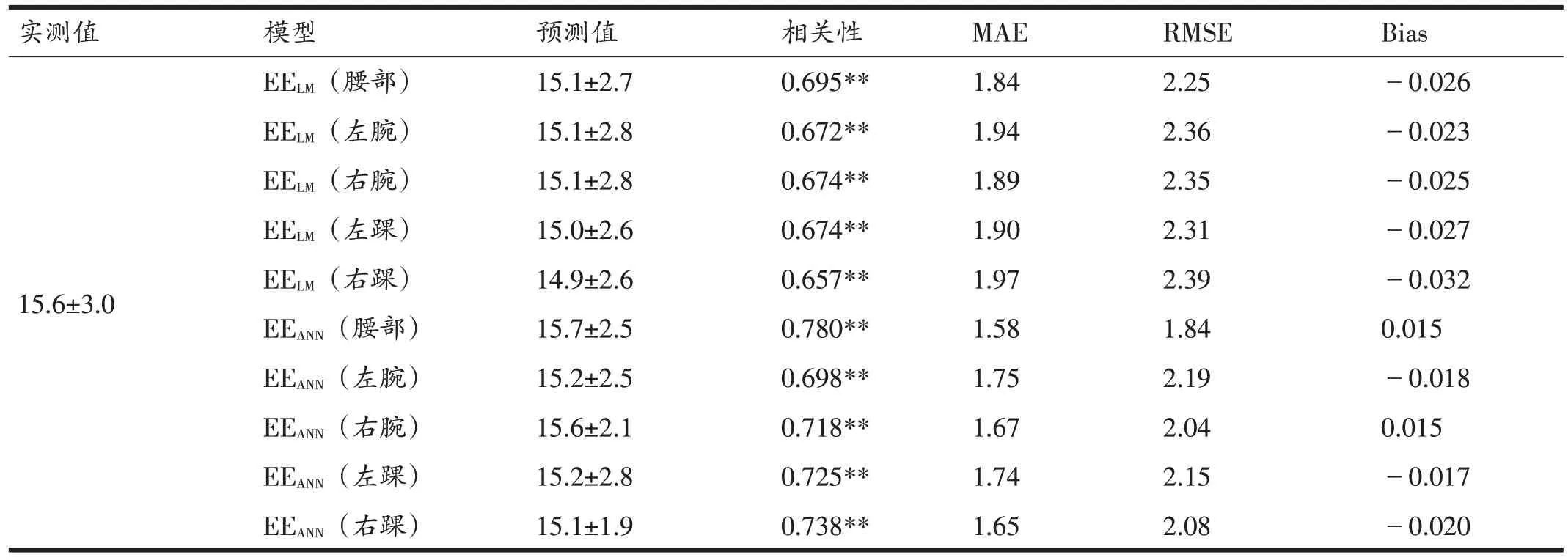
表6 跳绳运动能耗预测模型预测情况

将不同加速度计部位所建立能耗预测模型的预测值与实测值进行Bland-Altman分析（图1），并计算不同加速度计部位所建立模型的预测结果与通过间接测热法所得实测值的一致性限度区间（表7），5个加速度计部位的线性回归模型和神经网络模型中所有的误差点均落在95%置信区间内，说明所有模型均具有较好的预测效果。

图1 不同模型跳绳运动能量消耗Bland-Altman散点图

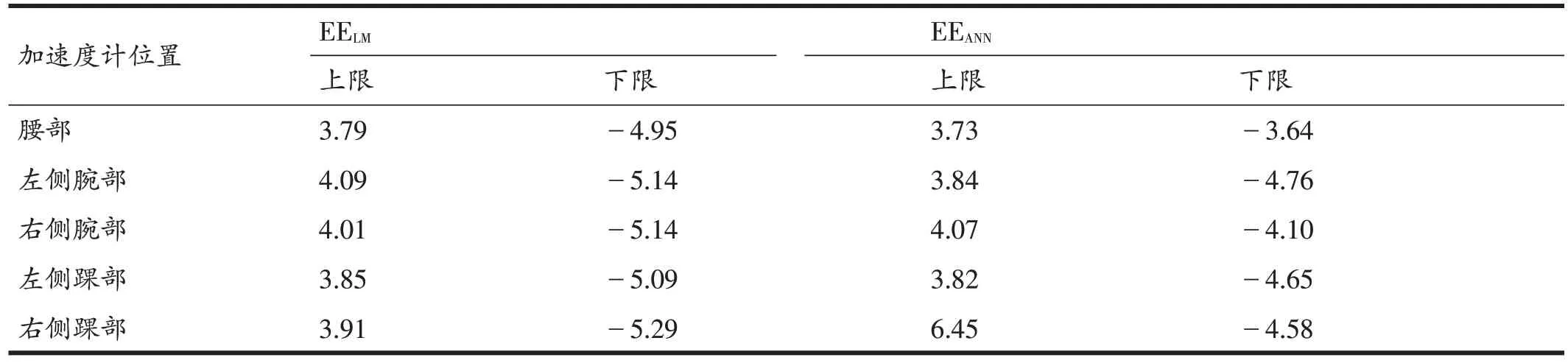
表7 各模型预测值与实测值一致性区间

为进一步验证各模型所得预测值与间接测热法所得实测值之间的一致性，本研究采用等效性检验中的可信区间法，判断预测值与实测值之间是否存在差异，具体结果见表8。依据加速度计所建立的线性回归模型预测值的90%置信区间均未落入实测值等效区间内，而依据加速度计所建立的神经网络模型预测值的90%置信区间均落在了14.06～17.18 的实测值等效区间内，说明不同加速度计部位所建立的神经网络模型预测值与实测值间具有等效性。

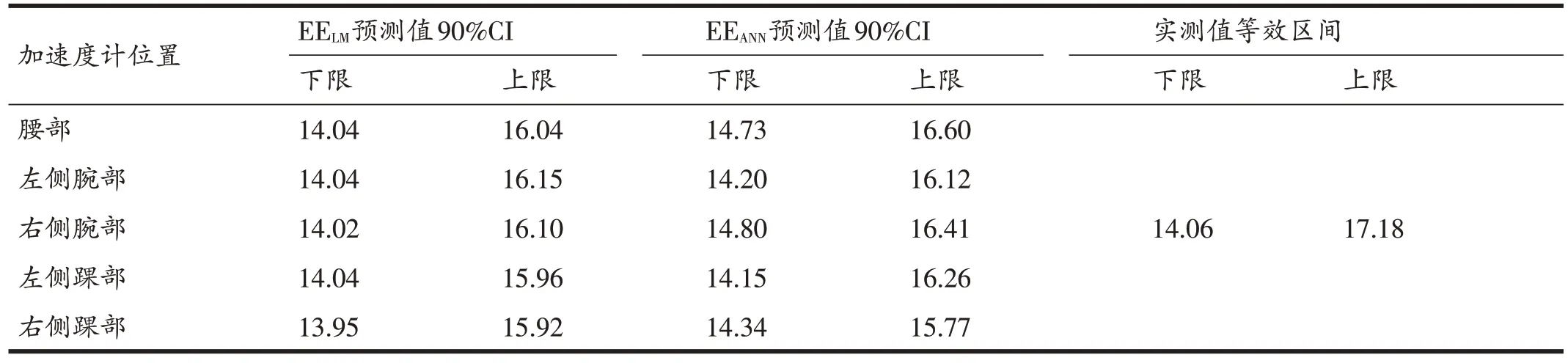
表8 各模型预测值与实测值的等效性检验

3 分析与讨论

3.1 单摇并步跳绳能量消耗特征

本研究通过间接测热法对36名受试者（男∶女=1∶1）进行了三种不同频率的单摇并步跳绳能耗测试，并对运动前静息和运动后过量氧耗期间的数据进行了采集。分析结果发现，低、中、高频率单摇并步跳绳运动过程中的平均心率分别为155.5、168.4 和168.3 次/min，依据心率强度区间，三种频率的单摇并步跳绳运动均属于短时间中高强度身体活动[22]。同时本研究还监测了单摇并步跳绳运动的总能量消耗数值EEtotal，即运动中和运动后过量氧耗阶段的总能耗减去静息能耗，结果显示低、中、高频率3 分钟单摇并步跳绳运动的总能量消耗分别为40.5、48.2 和45.4 kcal，表明单摇并步跳绳运动不仅可以在短时间内产生较高的能量消耗，并能够在运动结束后一段时间内维持机体高能量消耗。这与丁玲的研究结果相似[23]，该研究发现女大学生在频率为60、100和120次/min跳绳运动中所产生的平均能耗值分别为5.43、11.64 和11.33 kcal/min，但是该研究在分析跳绳能耗时没有减去静息能耗也没有考虑运动后过量氧耗阶段的能耗，这是目前国内外测试精准运动能耗的普遍不足[24]。同时本研究发现除EEtotal外，低频率跳绳时的EERS和EEEPOC也均低于中、高频率，而中频率和高频率跳绳运动在上述指标上基本保持一致，这可能与中频率（100次/min）跳绳相较高频率（130 次/min）跳绳的垂直地面反作用力（VGRF）、爆发力及摇绳幅度更大有关[3，25]，此外受试者在中频率跳绳期间的断绳次数较多，也增加了额外的能量消耗，从而导致中、高频率跳绳运动在能耗水平上差异较小。

3.2 各项生理指标与能耗的相关性

本研究将各项生理指标及不同部位加速度计计数与间接测热法所得的跳绳运动精准能耗值进行相关性分析发现，精准能耗值与性别之间的相关性具有统计学意义，由于男性与女性在身体成分（如体重、肌肉含量、去脂体重）和生理功能上均存在差异，因此，在本研究中男性的跳绳运动总能量消耗明显高于女性。此外，精准能耗值与体重、BMI、实际跳绳次数和ΔHR 也存在相关关系，而与运动中平均心率（HR）之间的相关性无统计学意义。这可能是由于心率仅在一定强度范围内与耗氧量呈线性关系[26]，这种线性关系在心率大于110次/min、小于150次/min期间最为显著[27]，说明心率能够有效监测中等强度身体活动的能量消耗。而短时间单摇并步跳绳属于高强度无氧运动[28]，同时结合本研究中低、中、高三种不同频率跳绳运动的心率区间为155.5～168.4次/min，均超出了与心率相关的强度区间，因此运动中平均心率与单摇并步跳绳能耗不存在相关关系。而ΔHR 为运动中平均心率与安静心率之差，通过对运动中净心率变化的计算可以更好地反映实际运动过程中的摄氧量及能耗变化[29]，因此，本研究在预测模型建立的过程中选取ΔHR反映心率指标的变化。对不同部位加速度计计数进行相关性分析发现，腰部加速度计除X轴计数值与精准能耗的相关性不存在统计学意义外，其余运动轴计数均与精准能耗存在相关关系，这可能是由于腰部加速度计的佩戴位置接近身体的重心[30]，相较手腕和脚踝对跳跃动作的敏感性更高。两侧踝部加速度计仅有VM 值及Y 轴计数值与精准能耗存在相关关系，而与感知垂直方向加速度的Z 轴计数值却不存在相关关系，这可能与低、中、高三种频率跳绳期间下肢关节屈伸幅度存在差异有关，低、中频率跳绳期间下肢关节的屈伸幅度较为一致[31]，而高频率跳绳期间髋、膝关节屈伸幅度明显减少，主要以踝关节快速屈伸完成跳绳动作[32]，因此与腰部相比，踝部加速度计可能受关节屈伸幅度影响，无法准确反映跳绳运动垂直方向的加速度变化。然而，同样产生较大运动幅度的两侧腕部的加速度计计数与精准能耗值之间却不存在相关关系，这可能与受试者在跳绳过程中摇绳的动作幅度不一致有关[33]。

3.3 能耗预测模型的建立

3.3.1 不同能耗预测模型准确性的对比

加速度计作为当前科研领域常见的能耗监测设备，已经在日常生活中得以普及，目前智能手机、手表等可穿戴设备的内置加速度计不仅能够满足日常身体活动的监测[34]，多数也已开发了监测专项运动能耗的功能。在针对跳绳运动能耗监测的早期研究中，大多研究都没有针对跳绳运动建立单独的预测模型，而是将跳绳运动包含在日常身体活动中进行研究[35]，因此导致预测跳绳运动能量消耗存在较大误差[13]。国内研究中仅有周洋等根据腰部加速度计VM 值建立了跳绳运动能耗预测的线性回归模型，其模型的决定系数R2为0.799[36]，略高于本研究所建立线性回归模型的R2，这可能与本研究测量跳绳运动总能耗时计算了运动后过量氧耗阶段的能量消耗有关。同时本研究还成功建立了预测单摇并步跳绳运动能耗的神经网络模型，尽管所有线性回归和神经网络模型均具有统计学意义，但是神经网络模型预测结果的MAE、RMSE 和Bias 值均低于线性回归模型，与实测值的相关性（r=0.780～0.698）也整体高于线性回归模型（r=0.695～0.657）。这与Alexander 等[19]的研究结果相似，他依据加速度计原始数据建立了慢跑、功率车和手臂弯举等日常身体活动能耗监测的线性回归和神经网络模型，其中腕部加速度计所建立神经网络模型的RMSE 和Bias 值均低于线性回归模型，与实测值的相关性（r=0.84～0.82）高于线性回归模型（r=0.73～0.71），说明应用神经网络模型能够有效提升加速度计的能耗预测效果。在Stewart等[37]针对青少年能耗的研究也得出了相同的结论，发现神经网络模型的RMSE 值较传统线性回归模型低30%～40%，同时Bias 值也低于线性模型，尤其是在监测跑步或中高强度剧烈运动期间，神经网络模型的预测值与实测值几乎不存在差异。本研究还针对两种模型进行了Bland-Altman 分析和等效性检验，结果显示两种模型的所有误差点均落入95%置信区间内，说明所有模型在预测值与实测值之间的一致性程度均较高[13]。但是在等效性检验中发现，只有神经网络模型预测值的90%置信区间落在了14.06～17.18 的实测值等效区间内，说明神经网络模型所得出的预测值与实测值之间具有等效性[38]。这与陈庆果等[20]的研究结果相一致，他在监测跳绳、篮球、羽毛球等日常身体活动时发现，与线性回归模型、Freedson 模型和Hendleman 模型相比，神经网络模型90%置信区间均落入等效区间内，说明神经网络模型与实测值之间具有等效性。综上所述，本研究结论进一步证实了神经网络模型较线性回归模型在加速度计预测单摇并步跳绳运动能耗时的优势，并且这种通过机器学习改善能耗预测准确性的方法将成为未来专项运动能耗监测的新趋势。

3.3.2 不同部位加速度计预测模型准确性对比

本研究中结合单摇并步跳绳动作模式选取的加速度计佩戴位置为腰部、两侧腕部和两侧踝部，在不同部位加速度计所建立的线性回归模型中，发现依据腰部加速度计所建模型预测结果的MAE、RMSE 和Bias 均低于两侧腕部和踝部所建模型，同时与实测值的相关性最高为0.695，说明在加速度计所建立的单摇并步跳绳能耗线性回归模型中腰部加速度计的预测效果最好，这与解浩东等[39]的研究结果相似，他对比了腕部、腰部、大腿及踝部加速度计在4～8 km/h 慢跑期间的能耗监测结果，经检验发现腰部加速度计的误差范围在-4.1～3.4之间，相比其他部位更加稳定且与实测值无显著差异。Treey 等[40]针对上坡跑的研究中也发现，加速度计佩戴于腰部、胸部和下背部时所建立的线性回归模型预测结果的可靠性（ICC）为78.5%～79.5%，高于大腿和脚背部加速度计的72.2%和71.9%，说明针对跑步等周期性运动时腰背部加速度计的监测准确性更高。本研究在对比不同部位加速度计所建立的神经网络模型时也发现了相同的结果，依据腰部加速度计计数所建立神经网络模型的预测结果具有更低的MAE、RMSE和Bias值，分别为1.58 kcal/min、1.84 kcal/min 和0.015 kcal/min，同时与实测值的相关性最高为0.780，说明在不同部位加速度计所建立的神经网络模型中腰部加速度计的预测效果最佳。但在Mackintosh等[41]针对儿童身体活动的研究中，将9个不同部位加速度计所建立的神经网络模型进行对比，发现仅有腰髋部和胸部加速度计预测值与实测值的相关性（r=0.81）略高于两侧手腕加速度计（r=0.77～0.78），而不同部位加速度计模型的RMSE 和Bias 值之间却无显著差异，这提示神经网络模型可能可以提高手腕、脚踝等部位加速度计的能耗监测准确性。然而，在Vries 等[42]应用神经网络模型识别跑步、跳绳、自行车等日常身体活动的研究中发现，腰部加速度计对动作的识别率为77%，显著高于脚踝的68%，说明在实际应用加速度计监测多种身体活动时仍然更推荐加速度计佩戴于腰部，以确保正确的活动分类和能耗监测。综上所述，在本研究中各线性回归模型和神经网络模型中预测准确性最高的部位均为腰部，同时结合跳绳运动是垂直克服自身重力做功，腰部加速度计不仅可以有效感知垂直方向（Z轴）的运动变化，且在实际应用中配合心率带较腕部和脚踝具有更高的可行性。因此，本研究认为在不同频率跳绳运动能耗监测过程中腰部为加速度计的最佳佩戴位置。

4 结论

本研究在中国人群中使用间接测热法，以单摇并步跳绳能耗精准数据为基准，分别建立了心率联合加速度计的线性回归模型和神经网络模型，两种建模方式均以腰部加速度计所建立的预测模型准确性最高，其中，线性回归模型：EEmin（kcal/min）=-0.262-3.897×性别+0.103×ΔHR+0.440×BMI+ 0.000045×腰部加速度计VM 计数值；神经网络模型：输入性别、ΔHR、BMI 及腰部加速度计VM 值建立三层（4-6-1）BP 神经网络模型。同时在两种模型的对比中发现，神经网络模型对于单摇并步跳绳运动的能耗预测具有更高的精准度。未来，在大样本人群跳绳运动能耗监测中，可使用心率带和腰部加速度计建立神经网络模型预测单摇并步跳绳运动的能量消耗，为跳绳运动在全民健身中的推广提供参考依据。