核心素养导向下的解析几何中坐标法的再理解
——由2023年高考解析几何综合题引发的思考
王长友 韩佳琦 郭 菁
(北京市密云区第二中学)
2023年高考数学试题已经揭晓,在解析几何综合问题的考查中多套试卷不约而同的出现了“确定性的一般规律”的研究,看似偶然实则是考查学生的直观想象、逻辑推理和数学运算等基本数学素养,是在考查学生真实问题情境中应用所学知识与思想方法解决真实问题的核心素养落地的体现.众所周知,坐标法是解决解析几何的根本方法和灵魂,本文结合2023年几个高考解析几何综合题的分析与思考,希望教师在具体教学中提升在核心素养导向下的坐标法的理解.
一、高考真题重现与思考
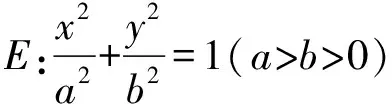
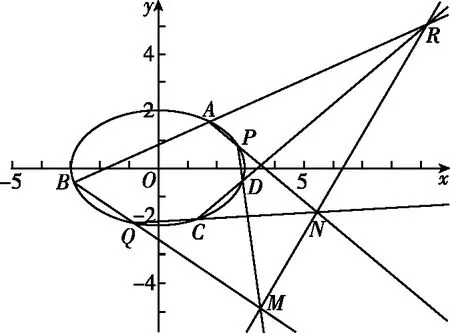
(Ⅰ)求椭圆E的方程;
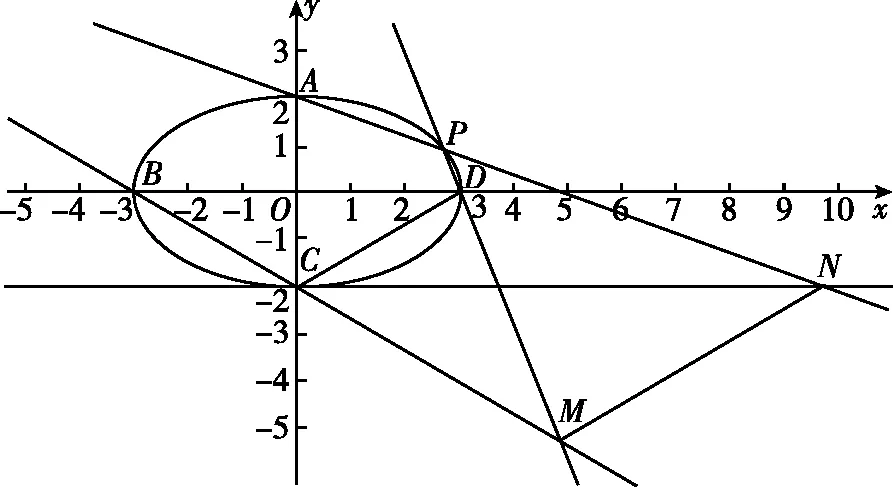
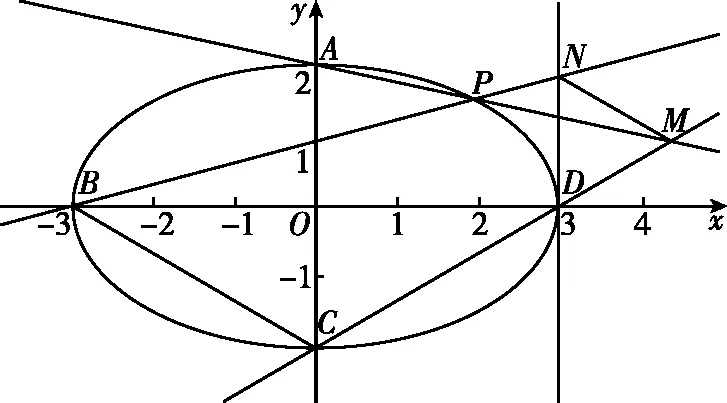
(Ⅱ)设P为第一象限内椭圆E上一动点,直线PD与直线BC交于点M,直线PA与直线y=-2交于点N,求证:MN∥CD.
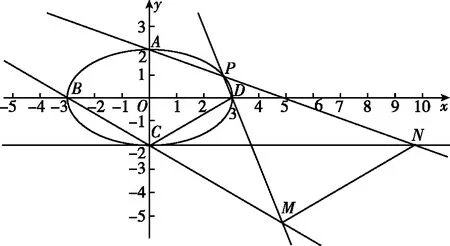
【分析】第二问依旧延续北京高考题题干简洁、位置关系清晰的风格,重点考查学生的坐标法解决解析几何综合问题的素养,考查学生的逻辑推理、数学运算素养等基本数学素养.
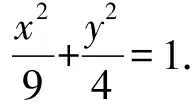
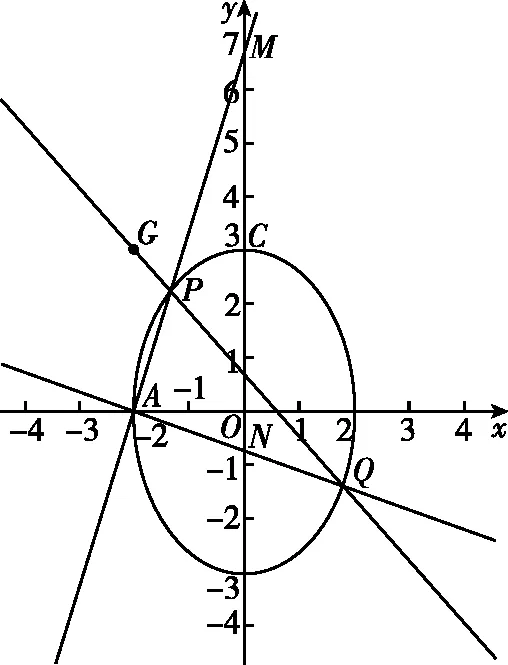
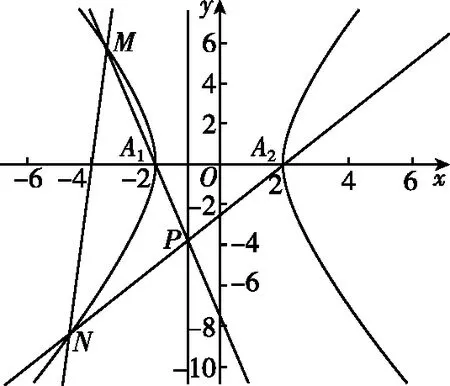
(Ⅱ)解法一:设P(x0,y0),易知(0 由A,P,N三点共线得kAP=kAN, 又因为P,D,M三点共线,得kPD=kMD, 又因为由A,P,N三点共线得kAP=kAN, 对此问题有如下几个思考: 【思考一】若将求证结论改为证明:直线MN的斜率为定值.显然问题本质不变,但是对学生来说,实际难度会加大. 【思考二】若将问题改为设P为第一象限内椭圆E上一动点,直线PA与直线y=-2交于点N,过点N作与CD平行的直线MN与直线BC交于点M,求证:P,D,M三点共线. 联立消去y并整理得(4+9k2)x2+36kx=0, 所以kPD=kMD,亦即P,D,M三点共线. 【思考三】设P为第一象限内椭圆E上一动点,直线AP与直线CD交于点M,直线BP与直线x=3交于点N,求证:MN∥BC. 解题思路分析:此问题与原问题本质是姊妹题,解决问题只需要将原问题的对应关系相应改变即可得证,不再赘述. 【思考四】回顾此问题解题过程,可以发现当动点P在其他象限时,结论不变.因此追加思考此问题的几何本质应该是什么? 由射影几何帕斯卡定理:椭圆E上有六个点A,B,Q,C,D,P,直线BQ与直线DP交于点M,直线AP与直线CQ交于点N,直线AB与直线CD交于点R,则M,N,R三点共线.反观北京此道高考题就是将上述情形进行了特殊化和具体化而得来. (Ⅰ)求C的方程; (Ⅱ)过点G(-2,3)的直线l交C于点P,Q两点,直线AP,AQ与y轴的交点分别为M,N,证明:线段MN的中点为定点. (Ⅱ)解法一:对于第二问常规解法具体过程不再赘述,只探讨如何便捷找出定点.若直线l与椭圆相切于上顶点时,此时P,Q与上顶点重合,此时直线AP,AQ与y轴的交点M,N重合为上顶点,显然可以大胆预测线段MN的中点即为(0,3),下面只需证明即可. 解法二:换个思路可得如下解法. 设直线AP的方程为y=m(x+2),直线AQ的方程为y=n(x+2),易知m,n存在且m≠n.设P(x1,y1),Q(x2,y2),M(0,yM),N(0,yN). 令x=0,则得yM=2m,yN=2n. 又因为G,P,Q三点共线,即kGP=kGQ, 将x1,y1,x2,y2代入得 进一步化简,并整理得(2m-3)2=(2n-3)2. 因为m≠n,所以2m-3=3-2n, 对这个问题进行重新梳理,有如下反思: 【思考一】上述问题条件不变,可以变为证明:直线AP,AQ的斜率之和为定值. 简要分析解题思路,结合解法一的常规思路可以通过计算kAP+kAQ得证;回顾解法二就可以发现kAP+kAQ=3. 【思考二】若改变问题形式为过点A(-2,0)分别作两条直线AP,AQ且满足直线AP,AQ的斜率之和为定值3,证明直线PQ过定点. 易知m-2k=0,直线PQ过点A(-2,0)显然不成立,因此得到m-2k-3=0,即直线PQ的方程为y=kx+2k+3=k(x+2)+3,显而易见过定点(-2,3). 【思考三】进一步思考过椭圆(或双曲线、抛物线)上一个定点分别作两条斜率之和为定值或斜率之积为定值的两条直线与椭圆(或双曲线、抛物线)相交,两个交点所形成的直线有什么特征? 【性质2】设抛物线的方程为y2=2px(p>0),点P(x0,y0)(y0≠0)是抛物线上的定点,PM,PN是该曲线的两条不同的弦,其所在直线的斜率分别为k1,k2,则: (Ⅰ)求C的方程; (Ⅱ)记C的左、右顶点分别为A1,A2,过点(-4,0)的直线l与C的左支交于M,N两点,M在第二象限,直线MA1与NA2交于P.证明:点P在定直线上. (Ⅱ)对于第二问的解答不做过多赘述,只说明如何确定结论即可. 结合上述三个2023年高考试题,可以发现在解析几何综合问题中,虽然情境问题千变万化,但是基本考查的特点为依托不同的圆锥曲线背景,以点、直线与圆锥曲线的位置关系考查为出发点,重点落实坐标法解决解析几何问题的应用,突出直观想象、逻辑推理、数学运算等基本数学素养的落地.高度契合了高考的“核心价值金线” “能力素养银线” “情境载体串联线”的“一核四层四翼”的要求. 教师要做一名研究型的智慧教师,一方面教师认真研究高考真题,这不是要以“考试为中心”的追随高考指挥棒效应,更重要的是要切实理解高考命题“一核四层四翼”的含义,把握数学教育的形势要求;另一方面教师要研究学生,抓住学生的痛点,准确把握学情,做到教学有的放矢.因此,教学中要切实提升对核心素养导向下的坐标法的理解. 教师要加强学习与认真研读新课标,明确课标要求.深入思考解析几何教学,教师要明确“解析几何是什么和解析几何如何做”这两个基本问题.新课标明确指出,解析几何的本质是“研究对象是几何图形,研究方法主要是代数方法”;解析几何的学业要求是“根据具体问题情境的特点,建立平面直角坐标系;根据几何问题和图形的特点,用代数语言把几何问题转化为代数问题;根据对几何问题(图形)的分析,探索解决问题的思路;运用代数方法得到结论”.这就是解析几何的核心标准,教师在教学中要把要求转化为具体的实践过程.即 单元教学将教学目标集中地把握与单元整体结构的有机整合,创建一种有利于学生学科思维发展和学科能力的提升的教学设计策略,充分体现学科的整体性、逻辑的连贯性、思想的一致性、方法的普适性、思维的系统性,切实防止碎片化教学;从学生的发展角度体现学生发展与认知的基本规律、学习是学生主动建构的过程、是培育和落实育人的过程.具体到解析几何教学,主要体现在整体把握点、直线、曲线的研究方法与研究内容的一致性,整体从坐标法的研究路径认识解析几何,整体从发展学生数学素养的角度去关注教学过程性的层次性、差异性. 解析几何综合问题体现了研究对象要素关系的复杂性、解决方法的综合性等特点,教学中教师要宏观引导学生明确研究本质,把握运动变化和数形结合分析问题、解决问题的关键过程.从运动变化过程分析,可以明确解析几何是在研究点、直线、圆、圆锥曲线等基本研究对象在运动变化过程中呈现的“变与不变”的规律,抓住运动过程分析,就可以抓住各要素间的联系,进而转化为代数关系研究.从数形结合过程分析,着重关注文字语言、图形语言、符号语言的基本转化,将数学问题直观展现,有利于学生对问题的深入理解;在此过程中,引导学生分析几何性质优化建立代数关系是重要的目的.把握这样两个过程,会使学生明白解析几何的问题发展过程,将复杂抽象问题条理化、具体化. 解析几何的学习重点发展学生的直观想象、逻辑推理与数学运算三个基本素养,三个素养有差异更有联系,是解决解析几何问题的有机整体. 直观想象是发现问题的基础也是解决问题的灵感和入手点,特别是在求解“确定性规律问题”时要强化直观感知,结合前面的实例中的猜想过程,教师在教学中要引导学生在具体问题中主动采用特殊位置、特殊情形、极限位置等对论证结论寻找方向,从而实现避免盲目使用复杂代数运算处理,体现在解决数学问题中“先猜后证”的探究一般性数学规律的思维过程. 逻辑推理素养是解决问题的核心,是问题不断深化与解决的指南,是指导学生有效通过代数运算解决问题的根基.应用价值体现在:一是在具体问题中要指导学生关注解析几何中运动变化的基本量之间的约束关系与联系,有效选择参数与合理选择代数关系进行问题刻画,实现问题思路清晰、路径具体;二是在逻辑推理的基础上分析、选择良好的几何性质实现代数关系的简洁,同时更要关注的代数关系运算处理的难易程度.只有在逻辑推理的基础上才能准确把握方法的合理性和运算的易于操作性. 运算素养是问题展开与完整解决的落脚点,是展现学生意志品质的载体.在教学中要有层次、有目的、有设计的分解运算难点和差异化的要求学生.特别是运算素养的有效落地是关键,因而教师必须提升对运算素养的重视与理解.在教学中,教师要通过典型问题指导学生建立整体的算法观,注意运算法则的准确理解、重视运算规律与特点的发现、养成明晰运算对象、预判运算方向、及时化简整理、有效应用运算策略的习惯,只有教师有目的的指导,学生才能够提升运算能力形成素养. 解析几何综合问题题目的本质是体现坐标法的应用,教师在课堂教学中可以实施“突出变化为手段,关注本质为核心”的变式教学,从而提升教学效率和激发学生的内驱力,实现教学相长的效果. 回顾前面问题的再思考过程,可以得到以下的变式教学的入手点.一是突出研究对象变化关注共性与联系,解析几何的基本研究对象是点、直线、曲线,重点是研究对象间的关系.教师要擅于在圆、椭圆、双曲线、抛物线的四种基本曲线中“随时切换”,用相同的背景问题在不同的曲线中展现发散学生思维,引导学生从数学的眼光去发现圆锥曲线中的相似性质就显得水到渠成,让学生体验到坐标法的魅力.二是突出命题形式变化关注逻辑规律,解析几何综合问题存在大量相关性问题,此类问题体现了基本的数学逻辑变化,因此教学中从改变已有常见命题的基本形式入手,可以重点探究原命题的逆命题,这会激发学生的研究兴趣,发现“创新结论”;三是突出数学运算的功能关注数学研究根基,运算既是数学技能,更是在解析几何乃至数学的发展过程中发现数学问题与数学规律的重要思想方法,因此主动引导学生在研究问题中关注“加减乘除”的基本运算关系,实现对问题的“突变”,通过此类变式会产生大量的“奇怪问题”,既有学生高中可以解决的,更会有不能解决的,但是学生对解析几何的理解会更深入. 变式教学要求教师首先勤于思考、善于思考,然后在教学中引领学生主动思考,就会激发学生的创造性.变式教学的核心是实现引导学生学会尝试“用数学的眼光观察世界、用数学的思维思考世界、用数学的语言表达世界”的数学教育价值,同时学生也能体会到数学的逻辑美、奇异美.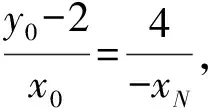
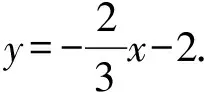
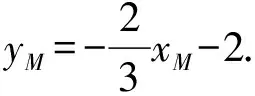
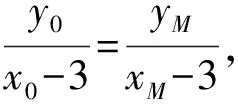
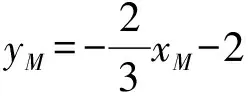
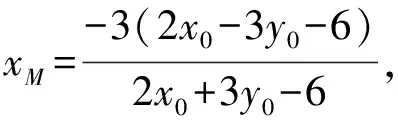
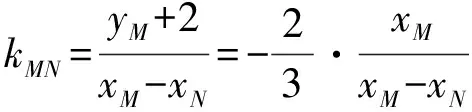
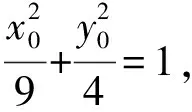
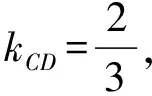

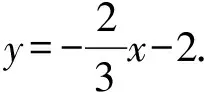
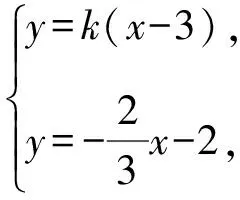
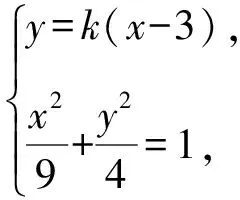
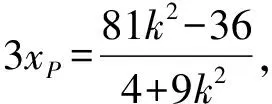
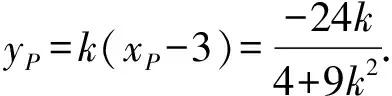
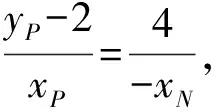
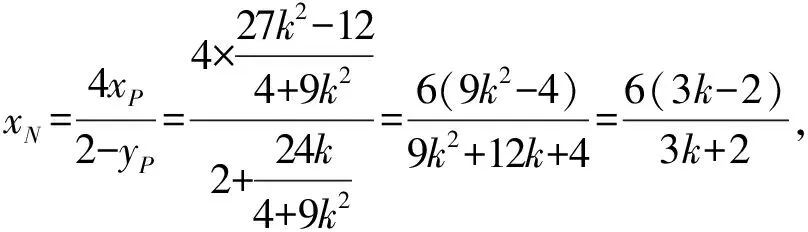
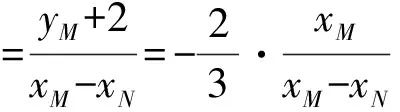
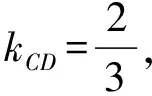
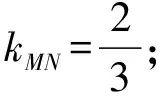
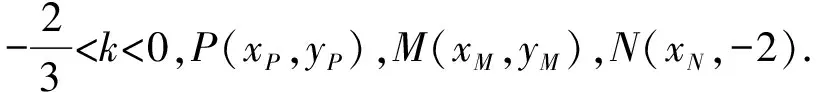
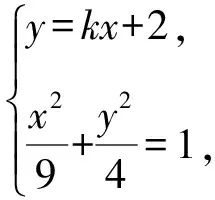
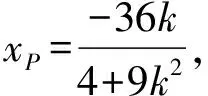
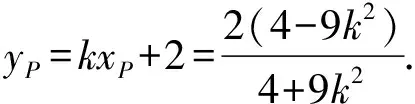
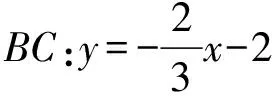
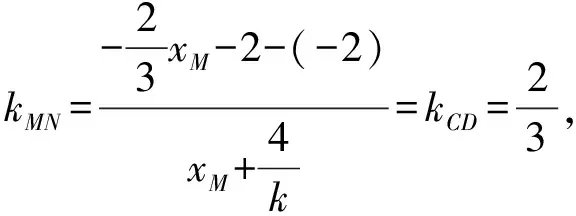
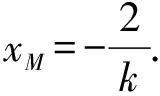
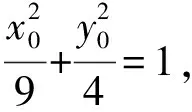
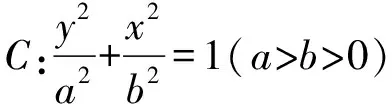
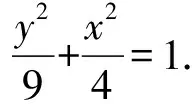
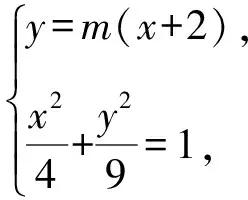
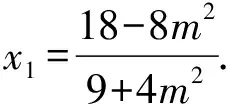
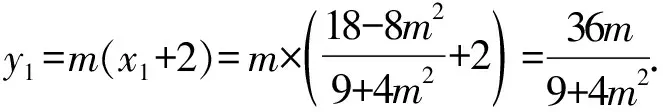
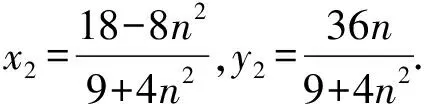
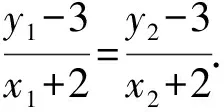
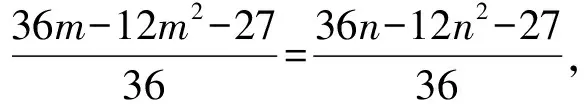
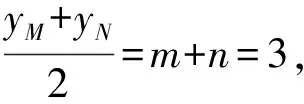
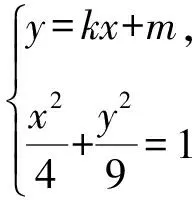
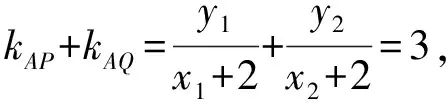
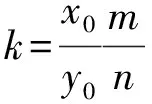
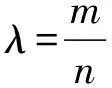
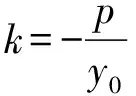
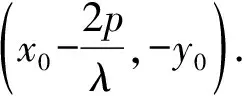
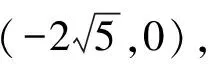
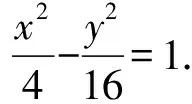

二、解析几何教学再思考
1.依托单元教学策略整体把握教学

2.把握运动变化和数形结合两个关键过程的分析
3.抓实直观想象、逻辑推理与数学运算三个素养的发展
4.重视变式教学提高效率


