求向量最值步履维艰,构隐圆模型大道通天——谈向量最值问题中几种常见的“隐圆”模型

唐 洵

(福建省福清第三中学)

平面向量的最值与范围问题是全国高考以及地市质检中的热点问题之一,其中有一部分问题,在充分剖析题设条件、合理构建知识联系后,可以发现其与圆的最值问题息息相关,因此在解题时,若是可以构造“隐圆”模型,便能实现数形结合,使得计算化繁为简.那么常见的“隐圆”模型有哪些?如何通过向量的条件联想到“隐圆”模型的构建?下面笔者结合相关例题进行说明,旨在对读者有所帮助.

模型一、定义圆

平面内到定点(a,b)的距离等于定长r的点的轨迹叫作圆,该定点(a,b)为圆的圆心,定长r为圆的半径,此时圆的标准方程为(x-a)2+(y-b)2=r2;在向量问题中,若遇到|a|=λ(λ>0)或|a-b|=λ(λ>0)(此时a或b为定向量)等条件时,可以考虑构造此模型,用圆的标准方程、一般方程或参数方程进行解题.

( )

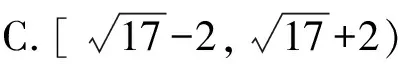
【答案】D

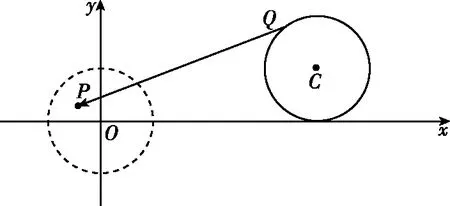
图1

【例题2】(2022·福州二模)已知平面向量a,b,c均为单位向量,且|a-b|=1,则(a-b)·(b-c)的最大值为

( )

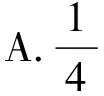
【答案】B

模型二、直径圆

圆的直径所对的圆周角为直角,因此当两个向量相互垂直时,可以选择一个共同的起点,则该起点在以两个向量的终点构成的线段为直径的圆上.在向量问题中,向量a,b的垂直条件体现为=90°,a⊥b,a·b=0,|a|2+|b|2=λ(λ>0)等,另外,以A(x1,y1),B(x2,y2)为直径端点的圆的方程为(x-x1)(x-x2)+(y-y1)(y-y2)=0.

( )

【答案】B

图2

【例题4】(2023·湖北名校联盟三测)已知平面向量a,b,c满足|a|=|b|=a·b=2,且(b-c)·(2b-c)=0,则|a-2c|的最大值为

( )

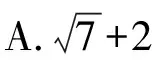
【答案】D

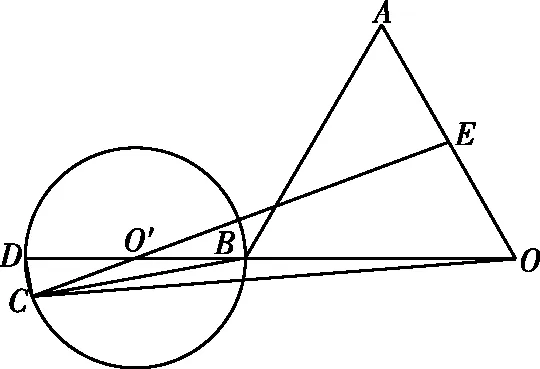
图3

模型三、向量圆

( )

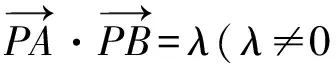
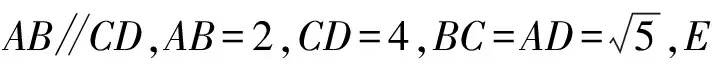
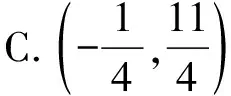
【答案】D

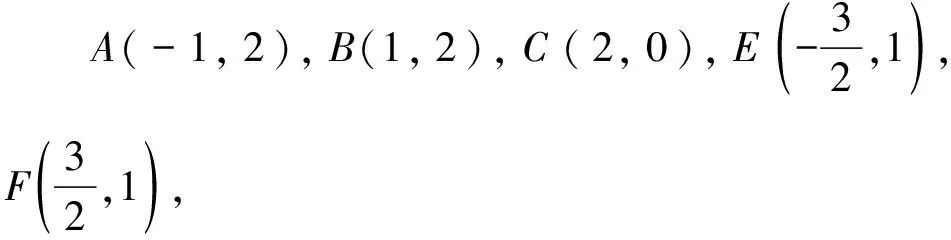
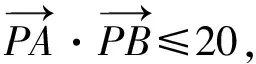
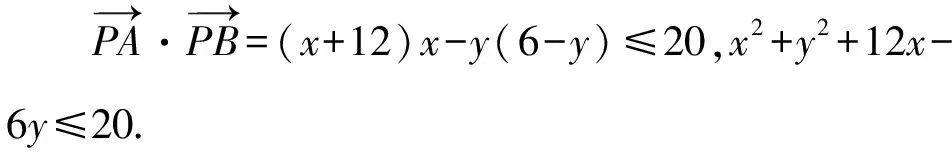
模型四、比例圆(阿波罗尼斯圆)

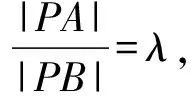
【例题7】平面向量a,b满足|a|=3|b|,且|a-b|=4,则a与a-b夹角的正弦值的最大值为

( )

【答案】B

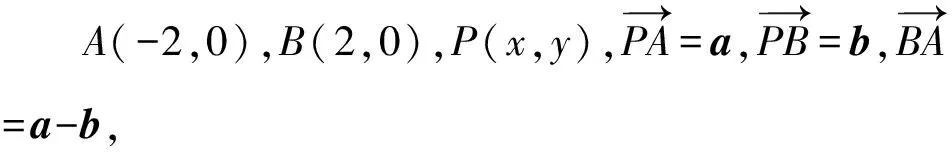
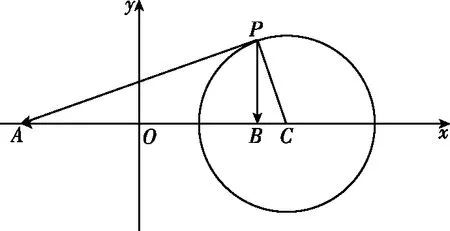
图5

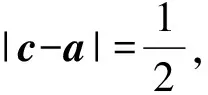
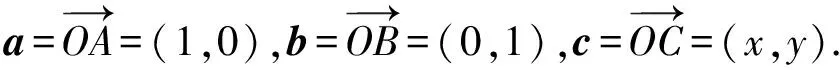
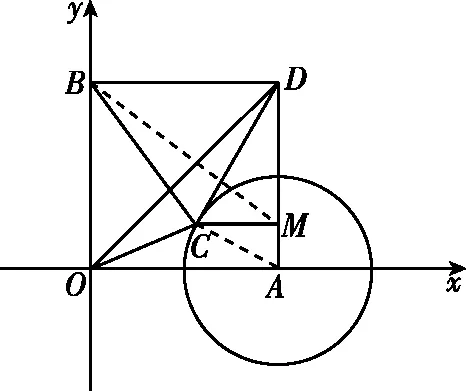
图6

模型五、外接圆

在三角形中,若遇到一边一对角问题,可以考虑构造此三角形的外接圆,从几何的角度进行解题.同样的道理,在向量问题中,若两个或三个向量可以构造出一个三角形(如a,b,a-b),且给出一边一对角的条件,可以考虑构造外接圆模型进行解题.

( )

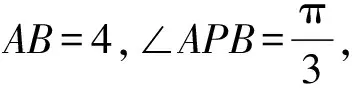
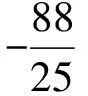
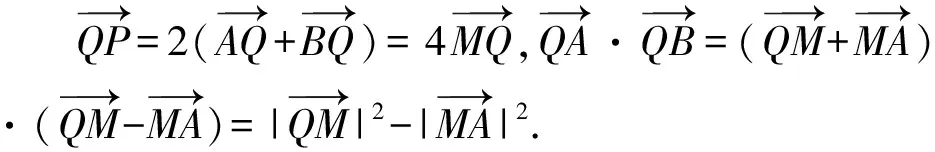
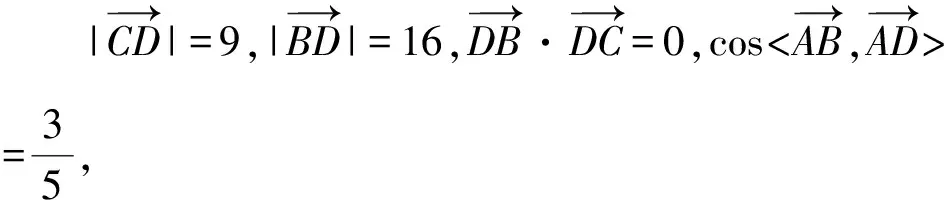
A.27 B.16 C.10 D.25

【答案】A

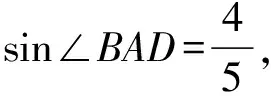
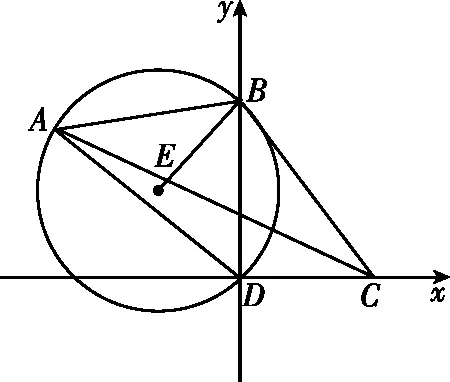
图7

模型六、四点共圆

圆内接四边形的对角互补;反之,若某四边形的对角和为180°,则该四边形的四个顶点共圆.在向量问题中,只需有三个向量,选取1个共同起点,加上3个终点,便可构成一个四边形,若该四边形满足上述条件,可以构造“隐圆”模型进行解题,四点共圆模型可以认为是外接圆模型的延伸.

( )

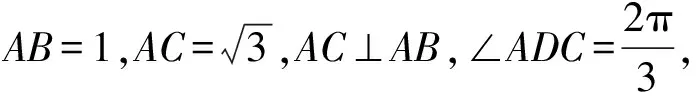
【答案】D

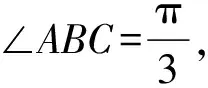
【答案】2

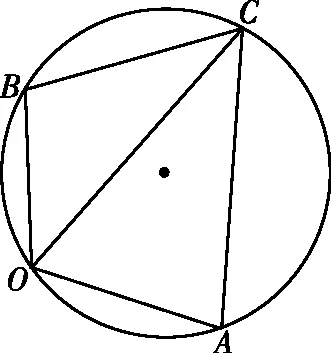
图9

模型七、极化圆

【答案】15

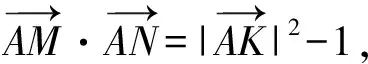
图10

【例题14】已知平面向量a,b,c满足a·b=60,|a-b|=4,|a-c|=1,则|c|的取值范围为________.

【答案】[5,11]

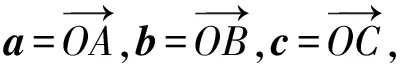
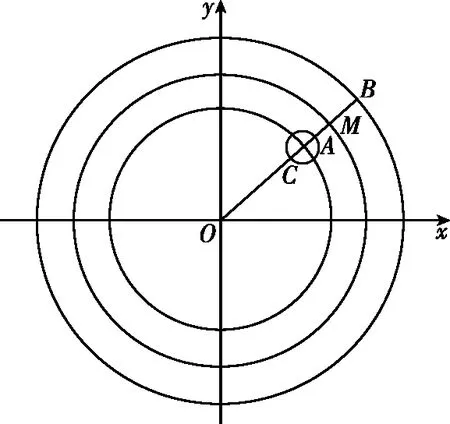
图11

图12