基于因式分解的压轴题最值方法探究

刘昌领

(湖北省通山县第一中学)

最值问题是高中数学的重要内容之一,也是高考数学热点内容之一.题目综合性较强,涉及到高中数学的诸多方面,因而方法灵活多变.笔者从一道能因式分解求最值的题目切入,通过多维度多视角分析,得到四种解法.

一、原题呈现

【例题】已知实数x,y满足2x2-xy-3y2=1,则2x2+3y2的最小值为________.

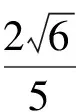
【分析】观察条件式子可知:左边是二次式,且能因式分解,要求的式子也是二次式,所以可以考虑:常规换元、三角换元、极坐标换元、利用导数求最值、或者基本不等式求最值.

二、解法探究

解法一:(因式分解+换元1)

∵2x2-xy-3y2=1,

∴(2x-3y)(x+y)=1.

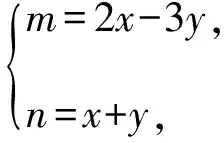
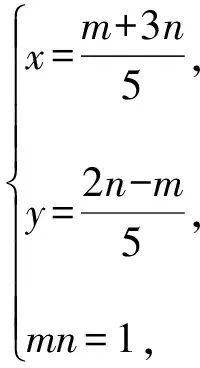
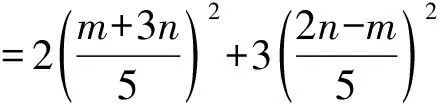
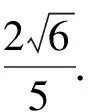
【评注】观察等式左边是二次三项式,巧妙地发现能进行因式分解,通过换元,再借助基本不等式成功地求出最小值.

解法二:(因式分解+换元2)

∵2x2-xy-3y2=1,

∴(2x-3y)(x+y)=1.

令t=2x-3y,

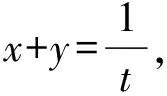
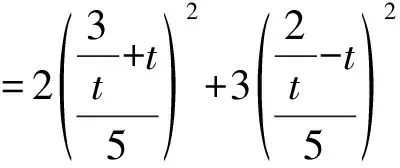
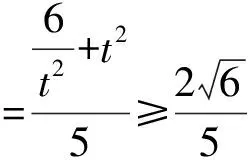
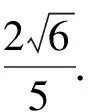
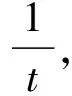
解法三:(因式分解+三角换元)

∵2x2-xy-3y2=1,

∴(2x-3y)(x+y)=1.

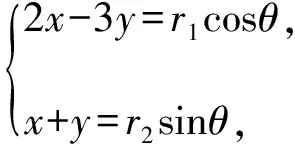
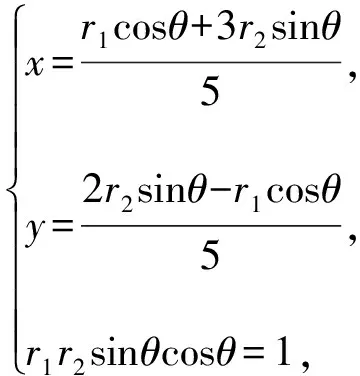
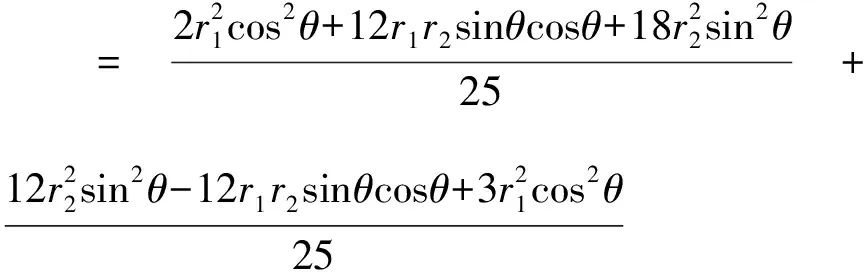
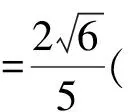
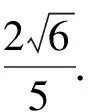
【评注】本法在因式分解基础上,应用三角换元,再借助基本不等式求出最小值.

解法四:(三角换元+分离常数+基本不等式)

∵2x2-xy-3y2=1,

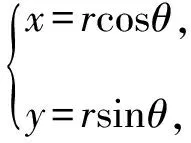
则2r2cos2θ-r2sinθcosθ-3r2sin2θ=1,

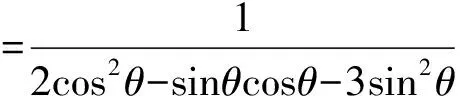
∴2-tanθ-3tan2θ>0,

∴(tanθ+1)(3tanθ-2)<0,

∴2x2+3y2=2r2cos2θ+3r2sin2θ

=r2(2cos2θ+3sin2θ)

令u=2x2+3y2,

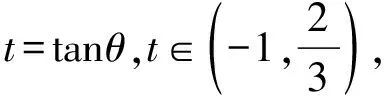
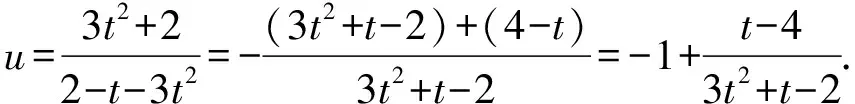
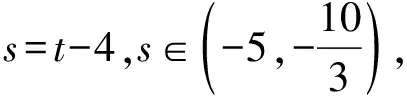
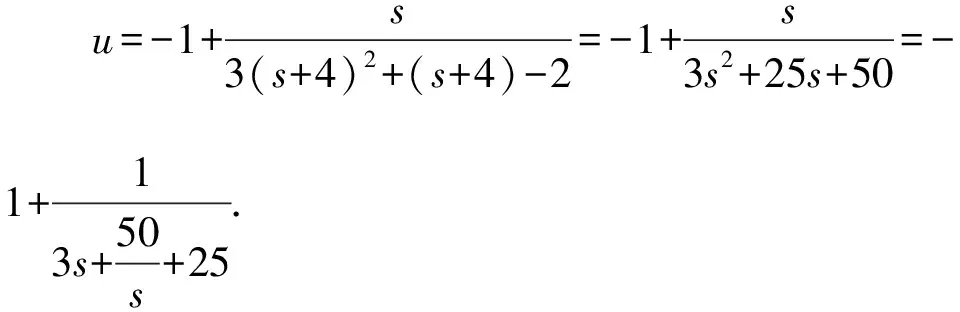
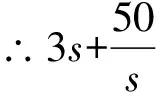
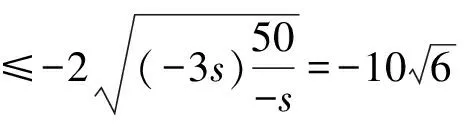
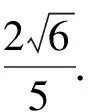
【评注】本法是先通过观察出齐次式,再进行两次换元,分离常数,最后利用基本不等式求最值.注意取等条件,即取得等号的s值是否在s的取值范围内.

三、变式训练

【变式1】已知实数x,y满足x2+2xy-3y2=1,则x2+y2的最小值为________.

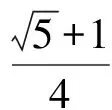
解法一:(因式分解+换元)

∵x2+2xy-3y2=1,

∴(x+3y)(x-y)=1,

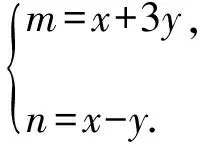
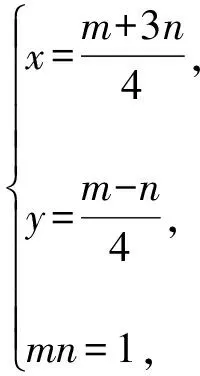
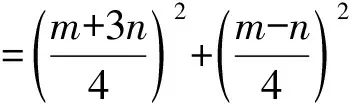
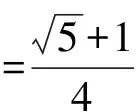
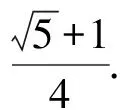
解法二:(三角换元+“1”的代换+判别式法)

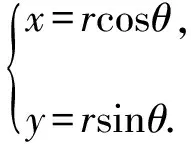
则r2cos2θ+2r2sinθcosθ-3r2sin2θ=1=sin2θ+cos2θ,

∴(r2-1)cos2θ+2r2sinθcosθ-(3r2+1)sin2θ=0,

等式两边同时除以cos2θ,得

(3r2+1)tan2θ-2r2tanθ-(r2-1)=0,

它是关于tanθ的一元二次方程,该方程有解,

∴Δ=4r4+4(3r2+1)(r2-1)≥0,

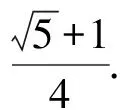
【评注】本法很巧妙,直接三角换元,关键是“1”转化为“sin2θ+cos2θ”,得到齐二次式,合并同类项之后再两边同时除以cos2θ,转化为关于tanθ的一元二次方程,利用判别式Δ≥0,得到r2的范围,而x2+y2=r2,即可求出x2+y2的最小值.

本题与例题的不同之处在于:例题计算的式子2x2+3y2的系数之比不是1∶1,如果例题也用判别式法,则计算过程非常烦琐.

解法三:(三角换元+判别式法)

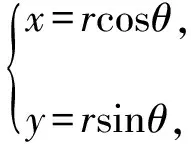
则r2cos2θ+2r2sinθcosθ-3r2sin2θ=1,

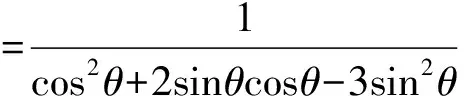
整理,得(3r2+1)tan2θ-2r2tanθ-(r2-1)=0,

下同解法二.

【评注】本法是在例题解法四的基础上进行变形,得到关于tanθ的一元二次方程,再利用判别式法,与解法二后半部分相同.

【变式2】已知x>1,y>0,且xy-2x-y+1=0,则x2+y2-2y的最小值为________.

【答案】7

【解析】∵xy-2x-y+1=0,

∴(x-1)(y-2)=1,

∵x>1,y>0,

∴m>0,n>0,

∴x2+y2-2y=(m+1)2+(n+2)2-2(n+2)

=m2+n2+2(m+n)+1

=7(当且仅当m=n=1,即x=2,y=3时,等号成立),

∴x2+y2-2y的最小值为7.

【评注】本题看到已知条件,要能“条件反射”想到因式分解.事实上,形如“Ax+By+xy+C=0”的式子,总能因式分解成为“(x+B)(y+A)=D”,之后即可进行换元:可以常规换元、三角换元、极坐标换元等.

【巩固练习】

1.已知x>0,y>0,且xy+2x+4y-41=0,则x+y的最小值为________.

2.已知实数x,y满足5x2-4xy-y2=5,则2x2+y2的最小值为________.

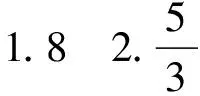
四、感悟

本文选题在基于能因式分解的基础上,进行换元,再结合基本不等式、判别式法、二次函数等方法求最值.