例谈解题教学的时效性

王胜锋

(广州市培英中学)

本文围绕数学解题教学的时效性,提出在日常教学中要用好课本中的例题、课后的习题、考试中的考题,注重基本方法的研读、重点知识的强化、变式题的练习等.

一、问题提出

检验教学的成果,普遍采用的方式是通过阶段性的调研考试、模拟考式或者期末考试,检测学生的学习情况,总结教学中的得与失.我们发现考试中的题目,似乎都在课堂中讲解过或者课外练习过,但面对常做常考的题目,还是有相当一部分学生存在计算上的错误、表达上的模糊、理解上的错乱等情况.学生反复出现这样的问题是教师的教学方法落后,学生的学习能力太差,还是教与学落实不到位?其实,数学教师一直都有这样的困惑.那么如何破解这种困惑呢?

二、解题教学在数学教学中的重要性

数学教学主要是围绕数学的核心与关键概念层层展开,通过对一些有关联性的问题的探讨,归纳和总结出新的概念、性质、法则、定理、结论等,可用于解决一系列与之有关的数学问题,所以解题教学就显得举足轻重了.教师在教学过程中,通过对数学问题的讲解帮助学生学会提出问题、分析问题、解决问题,可以说解题教学贯穿了整个数学课堂.

三、解题教学在数学教学中的时效性

1.时效性与实效性

时效性是指同一件事物在不同的时间具有很大的性质上的差异,它影响着决策的生效时间,进而决定了决策在特定时间内是否有效.信息的时效性是指从信息源发送信息后经过接收、加工、传递、利用的时间间隔及其效率.时间间隔越短,使用信息越及时,使用程度越高,时效性越强.

实际教学中,数学教师把教学的重心放在了教学的实效性上,只注重一节课、一个星期的效果,而忽视了教学的时效性,在用信息传达的过程中没有把时效性与实效性很好的结合起来.从两者的关系来看,时效性是实效性的必要条件和重要途径,实效性是增强时效性的根本目的和检验时效性的重要标志.

2.数学解题教学的时效性

要想提高数学教学的实效性,首先必须提高解题教学的时效性,才能从根本上解决教学过程中的困惑.解题教学的时效性就是在一定的时间内,学生能够准确表达解题思路,格式书写规范,并且能解决相关的数学问题.这里提到的一定时间是以实效性为标准,教师可以根据学生对知识的掌握的程度,灵活规定一个时间,可以是一周、一个月或一个学期.

四、提高数学解题教学时效性的基本方法

在解题教学过程中,教师不能只关注学生在课堂中的学习效果,也要关注学生在日后的学习中是否把所学的知识坚持运用下去,做到真正长时间的掌握,所以教师在解题教学中要把例题学习、练习、测试中出现的问题长期放在解题教学的过程中,反复强化,提高学生学习的效果.

1.用好课本的例题,更要选好例题的变式

课本中的例题是围绕本节内容展开的,既能对知识点进行巩固,又能为进一步学习打下基础.用好这些例题是课堂教学的首要任务.

只满足于弄懂课本上的例题是远远不够的.每一次的学习都是为日后打基础的,所以需要培养学生会用数学知识解决数学问题的能力.在这里,要求我们每位教师选好、设置好例题的变式,这是解题教学时效性的前提条件.

现以普通高中教科书《数学 必修 第一册》P227例10为例进行变式设计与分析.

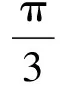
【分析】借助角α并利用三角函数,把矩形ABCD的长和宽表示出来,确定矩形ABCD面积的表达式,最后利用三角恒等变换和三角函数的性质就可以确定最大面积.接下来我们看一道对应的变式题.

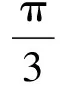
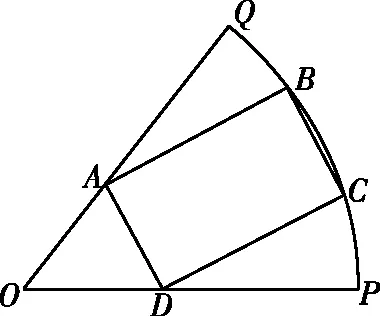
图1

图2

图3

【评注】通过课本中例题的变式,既可以加深知识间的相互联系,又可以帮助学生重构对数学思想、方法的认识和理解,对数学的学习大有裨益.

2.选好课后的习题,更要讲好习题的难点

随着课程改革和新教材的推进,数学教师更要注重对教材的利用,认真研读课后的习题,找出与课堂教学内容紧密相关、有利于补充知识并且难度和数量适度的习题给学生布置作业.不仅如此,教师通过批改作业,进一步发现学生学习上的不足.教师在课堂教学过程中,要求学生完全掌握课后习题,并且一定要安排时间来帮助学生消化习题的难点,为学生下一阶段的学习打下基础、树立信心,这是解题教学时效性的必要条件.

现以普通高中教科书《数学 必修 第一册》P23第5题为例进行分析.

【例题2】设a,b,c∈R.证明:a2+b2+c2=ab+ac+bc的充要条件是a=b=c.

【分析】在实际教学过程中,我们发现学生容易出错或不容易想到必要性证明的方法.

(1)条件和结论是相对的,它们可以相互转化,在说明充分条件和必要条件时,一定要明确条件和结论.很多学生分不清楚条件和结论,以为只要证明左边推出右边,右边推出左边就是证明了充要问题.

(2)在证明必要性时,如何由a2+b2+c2=ab+ac+bc得到a=b=c呢?应该从等式的结构特征出发,联想到与结构相近的完全平方公式a2+b2-2ab=(a-b)2,以及(a-b)2=0⟺a=b.

有时我们说这是数学中的技巧,但任何数学技巧都是对数学知识的应用,合理、正确的数学表达应该是自然的.解决数学问题的关键是要学会利用“路标”去到达“目的地”.获得“路标”的方法:一是观察,二是联想.讲好习题的难点不能仅满足于去到“目的地”,还要帮助学生学会发现“路标”,去到新的“陌生地”.

3.定好测试的试题,更要明确重难考点

数学的学习是需要内化的,而内化是需要时间的,所以数学的教与学是一个比较慢的过程,教师必须时刻关注学生的学习情况,帮助学生找到学习的方法,克服学习上的困难.因为日常教学时间紧、任务重,集中测试的机会自然难得,所以一定要精选题目,定好测试的试题.测试的目的不仅仅是了解学生对知识的掌握程度,更是在测试中帮助学生找到学习的动力和成就感,所以在每次测试中应该将平时学生练习中经常出错的试题作为测试的重要内容,保证学生彻底掌握,这是解题教学时效性的必然要求.

( )

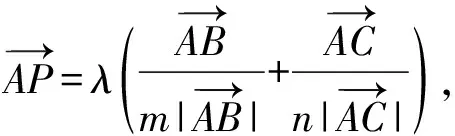
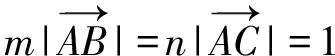
B.当m=n=1时,直线AP一定经过△ABC的外心

C.当m=cosB,n=cosC时,直线AP一定经过△ABC的垂心

D.当m=sinB,n=sinC时,直线AP一定经过△ABC的内心

【分析】该问题是关于共线定理和平面向量基本定理的综合应用,在多次考试中作为多项选择题的压轴题出现.在教学和复习备考中经历了以下几个阶段:

已知点O为△ABC平面内一点,

(1)初次尝试

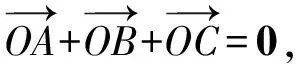
(2)继续深入

(3)重新认识

为了简化内心的证明过程,引入奔驰定理,将三角形的面积和向量联系在一起.首先利用比例的合比性质以及三角形的面积公式,以向量作为主干知识推理得出奔驰定理.接着应用奔驰定理验证重心、内心、外心、垂心对应的向量结论.

(4)最后确认

因为三角形四心的向量结论在表达形式上有很多,所以学生在掌握上是存在困难的,但结合奔驰定理,理解加记忆就可以很好辨别常用的结论.在最后一个阶段学生要自己评价是否完全掌握.有些学生掌握的好,不仅仅是他们记得牢、记得准,更重要的是他们重视最后一个阶段的学习和总结,能对自己的学习有一个评价,并且根据评价重新进行学习.

根据考试的结果,我们发现,虽然一直把某些特定的知识作为测试的重点,想通过多测试来进行知识的强化,但效果还是不理想,主要原因是教师不注重教学过程中解题的时效性,以为当时学生会了,以后就一定会,所以在设置测试的试题时,要关注学生重复出错的问题,把这类问题作为重复测试的核心,让学生经历再学习、再确认的过程,从而保证学习的效果.

五、总结