聚焦深度学习,发展核心素养——以一道教材习题为例

徐晓辉

(广东省惠州市惠阳中山中学)

本文以一道教材习题为基础,通过由特殊到一般、由浅入深的教学方法,一步步引导学生从简单的情景中发现问题、分析问题、解决问题,最终认识到问题的本质,进而提升学生对数学学习的兴趣,达到培养学生核心素养的目标.

一、经典再现,习题展示

选自人民教育出版社《数学 选择性必修 第一册》“3.3抛物线”的习题3.3复习巩固第6题.

【例题】如图,直线y=x-2与抛物线y2=2x相交于A,B两点,求证:OA⊥OB.

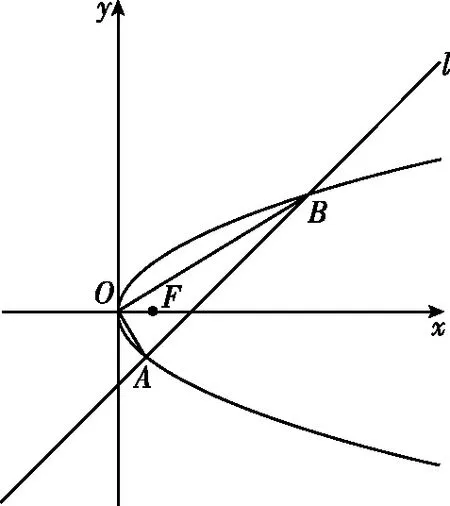
【证明】不妨假设A(x1,y1),B(x2,y2),则

消x得y2-2y-4=0,

由韦达定理知y1+y2=2,y1y2=-4,

所以x1x2=(y1+2)(y2+2)=y1y2+2(y1+y2)+4=4,

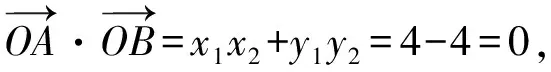
因此OA⊥OB.

二、角色互换,初步探究

【探究1】将已知条件和结论做一个简单的位置调换,即已知O为坐标原点,直线l与抛物线y2=2x相交于A,B两点(异于原点O),且OA⊥OB,直线l是否唯一存在?若唯一存在,求出直线l的方程.

【解析】由题意可设A(x1,y1),B(x2,y2),直线l的方程为x=my+t,其中t≠0,

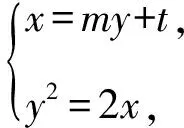
消x得y2-2my-2t=0,

由韦达定理知y1+y2=2m,y1y2=-2t,

所以x1x2=(my1+t)(my2+t)=m2y1y2+mt(y1+y2)+t2=t2.

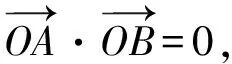
【评注】观察分析直线方程x=my+2发现,不管m如何变化,直线l均经过点(2,0),因此得出结论:已知O为坐标原点,直线l与抛物线y2=2x相交于A,B两点(异于原点O),且OA⊥OB,则直线l经过定点(2,0).

我们知道O不仅是坐标原点,同时也是抛物线y2=2x上的一个特殊的点.基于上述分析,不禁提出新的疑问:将条件OA⊥OB中的点O改换成抛物线上任意一点,是否存在类似的结论?

三、疑问呈现,逐个击破

【探究2】已知O为坐标原点,N为抛物线上的一点,直线l与抛物线y2=2x相交于A,B两点(异于点N),且NA⊥NB,直线l是否过定点?若直线l过定点,求出该定点.

消x得y2-2my-2t=0.

由韦达定理知y1+y2=2m,y1y2=-2t,

所以x1x2=(my1+t)(my2+t)=m2y1y2+mt(y1+y2)+t2=t2,

x1+x2=(my1+t)+(my2+t)=m(y1+y2)+2t=2m2+2t.

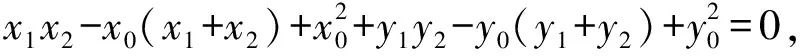
解得t=x0-my0,或者t=x0+2+my0.

当t=x0-my0时,直线l的方程可化为x-x0=m(y-y0),因此直线l过N点,与题意矛盾,舍去;

当t=x0+2+my0时,直线l方程可化为x-(x0+2)=m(y+y0),直线l过定点,该定点坐标为(x0+2,-y0);

因此直线l过定点,且该定点坐标为(x0+2,-y0).

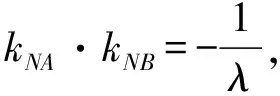
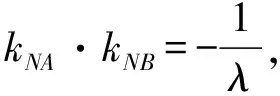
消x得y2-2my-2t=0,

由韦达定理知y1+y2=2m,y1y2=-2t,

所以x1x2=(my1+t)(my2+t)=m2y1y2+mt(y1+y2)+t2=t2,

x1+x2=(my1+t)+(my2+t)=m(y1+y2)+2t=2m2+2t.

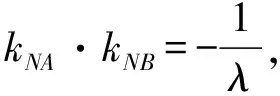
所以(x1-x0)(x2-x0)+λ(y1-y0)(y2-y0)=0,

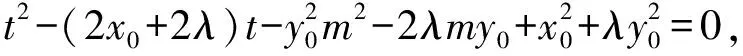
解得t=x0-my0,或者t=x0+2λ+my0.

当t=x0-my0时,直线l的方程可化为x-x0=m(y-y0),因此直线l过点N,与题意矛盾,舍去;

当t=x0+2λ+my0时,直线l方程可化为x-(x0+2λ)=m(y+y0),直线l过定点,该定点坐标为(x0+2λ,-y0);

因此直线l过定点,且该定点坐标为(x0+2λ,-y0).

在探究2和探究3的分析中,我们发现该定点的位置与抛物线上点N的坐标和直线NA,NB斜率的乘积有很强的关联.为了深化对该定点的认识,接下来探究:当抛物线的开口大小发生改变时,直线l经过定点的位置如何变化?

四、深化认知,直击本质

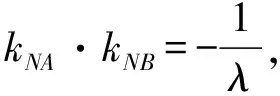
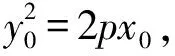
消x得y2-2pmy-2pt=0,

由韦达定理知y1+y2=2pm,y1y2=-2pt,

所以x1x2=(my1+t)(my2+t)=m2y1y2+mt(y1+y2)+t2=t2,

x1+x2=(my1+t)+(my2+t)=2pm2+2t.

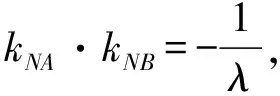
所以(x1-x0)(x2-x0)+λ(y1-y0)(y2-y0)=0,

解得t=x0-my0,或者t=x0+2pλ+my0.

当t=x0-my0时,直线l方程可化为x-x0=m(y-y0),因此直线l过点N,与题意矛盾,舍去;

当t=x0+2pλ+my0时,直线l方程可化为x-(x0+2pλ)=m(y+y0),直线l过定点,该定点坐标为(x0+2λp,-y0);

因此直线l过定点,且该定点坐标为(x0+2λp,-y0).

【评注】通过探究4不难发现,抛物线上点N到x轴的距离等于定点到x轴的距离.当直线NA,NB斜率的乘积不变时,改变抛物线上点N的位置,对应定点的位置也会相应发生改变,这些定点组成怎样的图形?

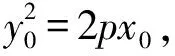
【探究5】已知O为坐标原点,N为抛物线上的一点,直线l与抛物线y2=2px相交于A,B两点(异于点N),直线NA,NB的斜率均存在,且kNA+kNB=μ,直线l是否过定点?若直线l过定点,求出该定点.

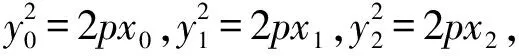
消x得y2-2pmy-2pt=0,

由韦达定理知y1+y2=2pm,y1y2=-2pt,

所以x1x2=(my1+t)(my2+t)=m2y1y2+mt(y1+y2)+t2=t2,

x1+x2=(my1+t)+(my2+t)=2pm2+2t.

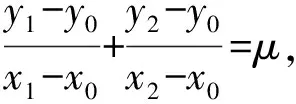
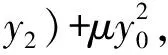
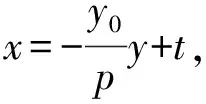
五、拓展应用,感悟反思

【练习1】已知抛物线E:y2=2px(p>0)的焦点为F,点P在抛物线E上,点P的横坐标为1,且|PF|=2,A,B是抛物线E上异于O的两点.

(Ⅰ)求抛物线E的标准方程;

(Ⅱ)若直线OA,OB的斜率之积为-4,求证:直线AB恒过定点.

【练习2】如图,已知抛物线C:y2=2px过点A(1,1),过点P(3,-1)的直线与抛物线C交于M,N两个不同的点(均与点A不重合).

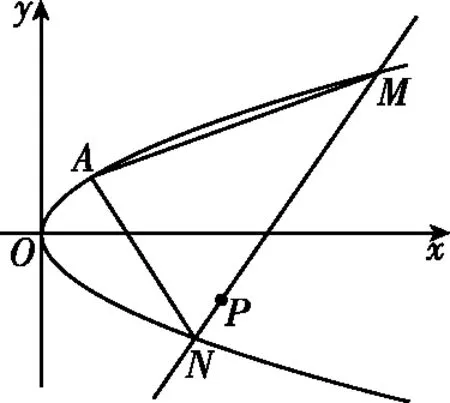
(Ⅰ)求抛物线C的方程及焦点坐标;

(Ⅱ)设直线AM,AN的斜率分别为k1,k2,求证:k1k2为定值,并求出该定值.

【练习3】已知抛物线C:y2=2px的焦点坐标为F(1,0).

(Ⅰ)求抛物线C的方程;

(Ⅱ)已知定点P(1,2),A,B是抛物线C上的两个动点,如果直线PA的斜率与直线PB的斜率之和为2,证明:直线AB过定点.

【练习4】已知抛物线C:y2=2px(p>0)经过点(1,2).

(Ⅰ)求抛物线C的方程;