解三角形问题中“爪”型结构的解题策略研究

杨媛媛 田万华

(湖北省赤壁市第一中学)

解三角形是高考中的重要考查内容,是考查学生思维能力、核心素养的重要载体,其中“爪”型结构的解三角形问题屡见不鲜,如中线、角平分线、高线等.下面通过对2023年高考部分解三角形真题的分析,总结这类问题的常见解题策略.

类型一、解三角形中有关高线问题

【例题1】(2023·新课标Ⅰ卷·17)已知在△ABC中,A+B=3C,2sin(A-C)=sinB.

(Ⅰ)求sinA;

(Ⅱ)设AB=5,求AB边上的高.

(Ⅱ)思路1.结合三角函数求解

如图,过点C作CD⊥AB于点D.

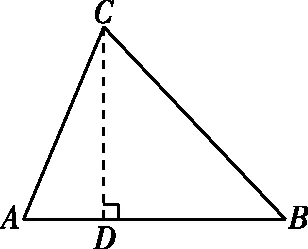
∴CD=BCsinB=6.

思路2.结合等面积法求解

思路3.结合两个直角三角形求解

如图,过点C作CD⊥AB于点D.

设CD=h.

∴h=6,即CD=6.

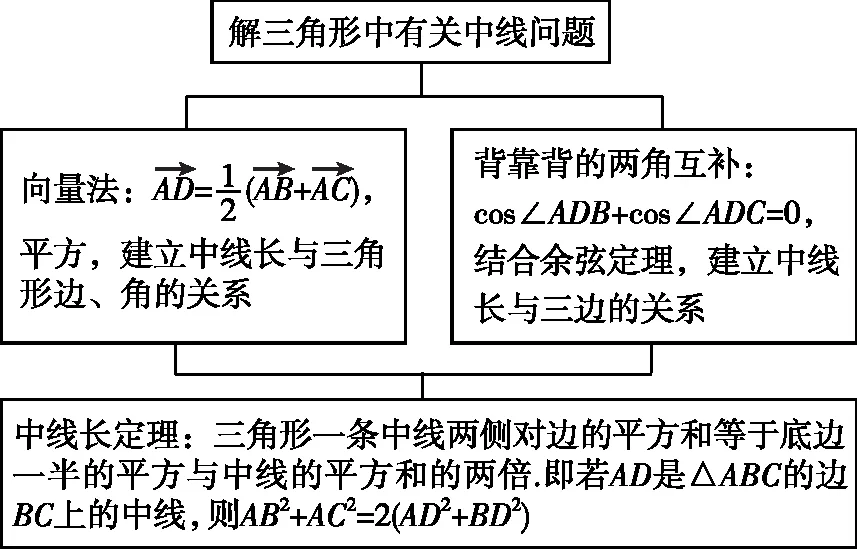
【归纳总结】

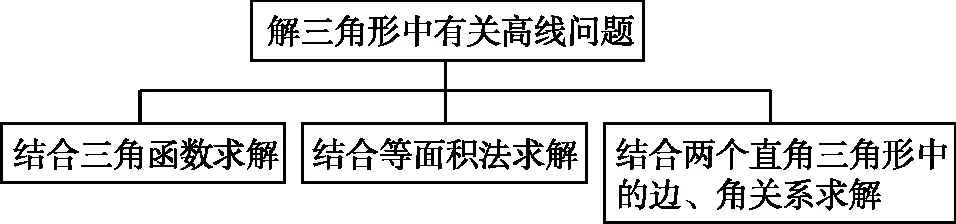
类型二、解三角形中有关中线问题

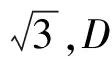
(Ⅱ)若b2+c2=8,求b,c.

【解析】(Ⅱ)思路1.借助向量工具

如图,

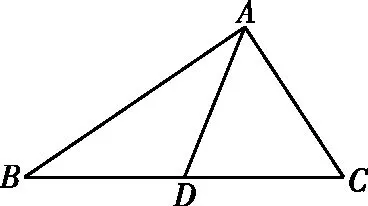
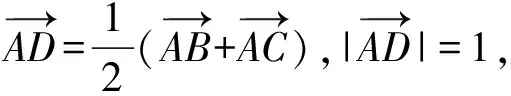
∴4=b2+c2+2bccos∠BAC.

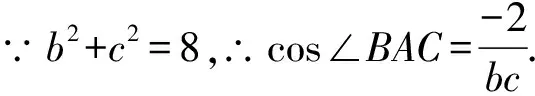
∵sin2∠BAC+cos2∠BAC=1,

∴bc=4,∴b=c=2.

思路2.利用背靠背角的互补关系

如上图,∵cos∠ADB+cos∠ADC=0,

∴b2+c2=2(AD2+BD2),

∴sin∠ADB=1,

∴由勾股定理,得b=c=2.

【归纳总结】

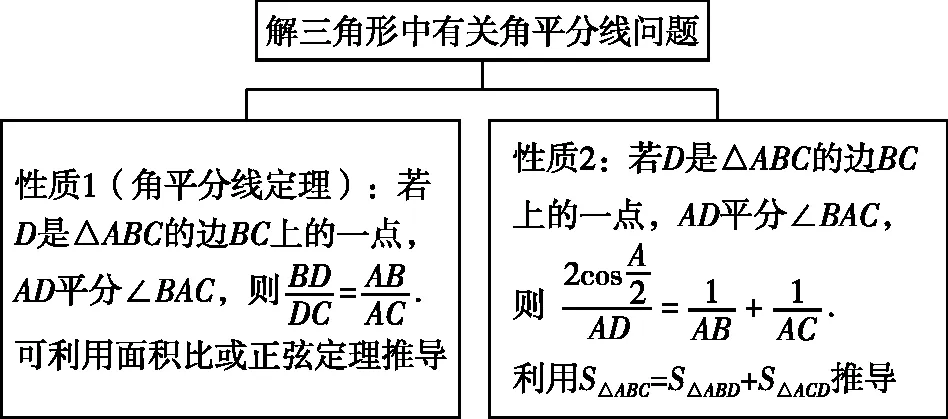
类型三、解三角形中有关角平分线问题

【解析】思路1.等面积法

如图,

令BC=a,AC=b,AB=c,

a2=b2+c2-2bccos∠BAC,

∵S△ABC=S△ABD+S△ACD,

∴AD=2.

思路2.向量法

如上图,在△ABC中,

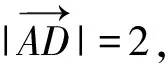
∴AD=2.

【归纳总结】

类型四、其他“爪”型问题

【例题4】(2023·全国乙卷理·18)在△ABC中,已知∠BAC=120°,AB=2,AC=1.

(Ⅰ)求sin∠ABC;

(Ⅱ)若D为BC上一点,且∠BAD=90°,求△ADC的面积.

【分析】本题在第(Ⅰ)问的基础上非常容易,但如果抛开第(Ⅰ)问,第(Ⅱ)问的解法就非常多,而且体现了爪型问题的常见解法.

(Ⅱ)思路1：如图,

∵BC2=AC2+AB2-2AB·AC·cos∠BAC,

在Rt△ABD中,

∵∠BAC=120°,

∴∠DAC=30°,

思路2：∵∠BAC=120°,∴∠DAC=30°.

∵S△ABC=S△ABD+S△ACD,

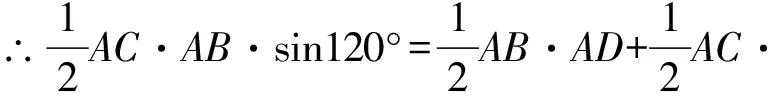
思路3：∵∠BAC=120°,

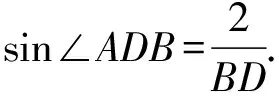
∵sin∠ADB=sin∠ADC,

∴BD=4CD,

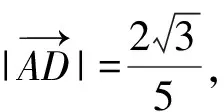
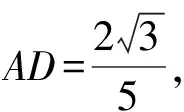
思路5：过C作AB的垂线,交BA的延长线于点E,

∵AC=1,∠CAE=60°,

∵AD∥CE,

∵∠DAC=30°,

【归纳总结】