基于算术优化算法的低压配电网故障区段定位方法
王欣阳,王瑞阳,魏云冰
(1.上海工程技术大学 电子电气工程学院,上海 201620;2.许昌电气职业学院,河南 许昌 461002)
随着社会经济的发展,我国低压配电网越来越复杂,居民用电需求日益增多。随着计算机技术和通讯技术的发展,为了提高居民用电质量,电网企业开始建设智能配电网和智能台区,用以监测居民的用电数据和故障报警信息[1]。通过对汇总数据进行分析,可以实现低压配电网故障区段定位。
目前,常见的故障区段定位方法有矩阵算法和群体优化算法。矩阵算法[2-3]具有计算简单、运算速度较快的优点,但需要获得较为准确的数据,当数据残缺时易造成误判或错判。群体优化算法有遗传算法(Genetic Algorithm,GA)[4-5]、粒子群算法[6-7]、蚁群算法[8]和免疫算法[9]等,这些算法计算速度快,但易陷入局部最优,因此准确度较差。文献[4]使用遗传算法对配电网进行故障定位,提高了配电网故障定位效率。文献[6]对粒子群算法进行二进制处理,并和遗传算法进行对比,结果表明二进制粒子群算法(Binary Particle Swarm Optimization,BPSO)具有更好的速度优势,收敛性更好。文献[7]对二进制粒子群算法进行改进,添加免疫算法,使其收敛速度和准确性再次得到提高。此外,蝙蝠算法[10]、灰狼算法[11]、正余弦算法[12]以及鲸鱼优化算法[13-15]等算法也被用于故障区段定位,但都需要较大的初始种群数量才能保证计算准确性,且部分算法也具有容易陷入局部最优的缺点。文献[11]通过对灰狼算法进行改进,加入遗传算法,使其准确度和收敛性均得到显著提升。文献[12]通过添加levy扰动策略使正余弦算法不易陷入局部最优状态。文献[13]通过添加调节搜索路径和最优邻域扰动算法使鲸鱼算法不会陷入局部最优且加快了收敛速度。
算术优化算法(Arithmetic Optimization Algorithm,AOA)[16-18]具有结构简单、收敛速度快以及精确度高等优点。本文运用该算法的全局寻优和局部寻优分开进行的特点,通过对判断为全局或局部的函数进行改造,使此算法在前期迭代中对局部寻优进行充分探索。仿真结果表明,与二进制粒子群算法、遗传算法和改进鲸鱼优化算法(Improved Whale Optimization Algorithm,IWOA)相比,算术优化算法能更快更准确地计算出故障区段。
1 低压配电网智能台区故障区段定位模型
低压配电网智能台区将获取各用户节点配电终端的信息汇总到低压配电自动化控制中心,并对汇总后的信息进行判断处理从而实现故障区段定位。
1.1 故障区段定位模型搭建
低压配电网智能台区将一个或多个用户划分为独立区段,每个区段均具有独立的配电终端,并且在每个用户节点上具有独立的配电终端,这些终端均具有数据传输功能。当终端后端发生故障时,终端通过通讯总线把故障信息发送到数据采集系统,通过对收集的信息进行合理分析判断从而实现有效的故障区段定位。
以图1为例,对节点进行编号,无分布式电源,因此各节点仅有无故障和有故障两种状态,如式(1)所示。
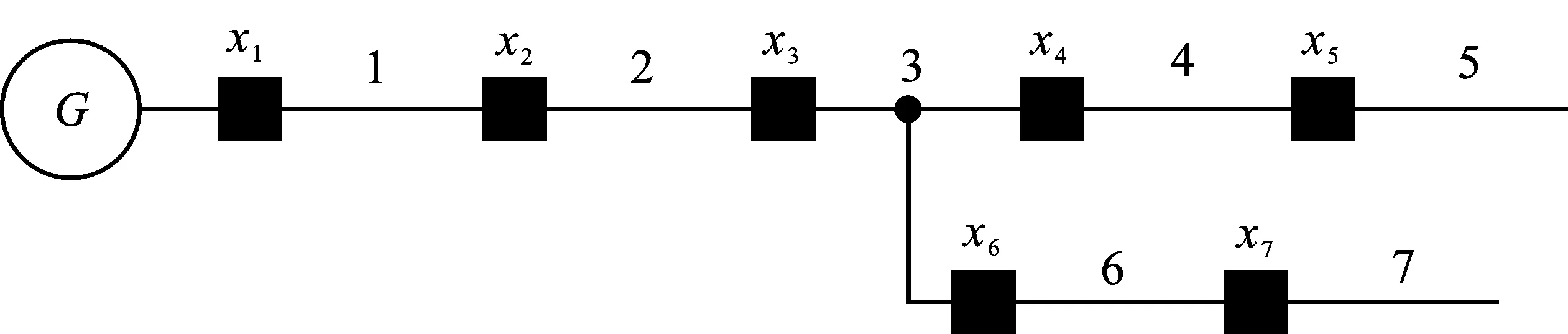
图1 简单配电网Figure 1. Simple distribution network
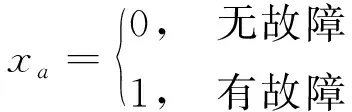
(1)
式中,xa为节点a的状态,a=1,2,……,7。
各节点的开关函数Ix1~Ix7如式(2)所示。
(2)
式中,“|”表示逻辑“或”。
1.2 故障区段定位适应度函数
本文采用的适应度函数为
(3)
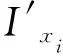
2 算术优化算法
算术优化算法[16-18]是一种新型元启发式算法,来源于简单的四则运算“加减乘除”,具有收敛速度快、精度高等特点。
算法初期对种群进行初始化,如式(4)所示。
(4)
式中,N为种群数量,在故障区段定位问题中定义N个解。N越大,解数越多,问题准确度越高,但计算时间随之增加。在本文中当N取50时,能获得最好的效果;n为探索空间维度,在故障区段定位问题中代表总节点数;x1,n为第1个解在第n维空间的位置。
在初始化种群时,先对X的N×n矩阵全部赋0,然后对矩阵X每行的每个元素进行赋值。定义r为服从[0,1]均匀分布的随机数,当r>0.5时,对元素赋1;当r<0.5时,对元素赋0,最后得到一个0~1分布的矩阵X。
在初始化种群后,算法设定了一个数学优化加速系数(Math Optimizer Accelerated,MOA)来控制算法的搜索阶段,即勘探阶段和开发阶段,如式(5)所示。
(5)
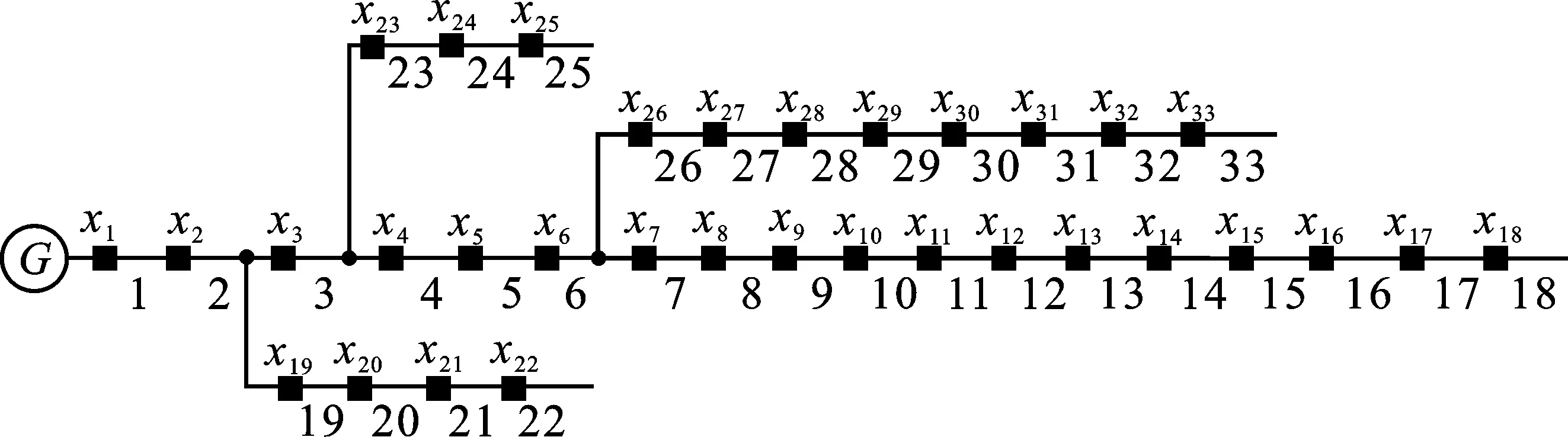
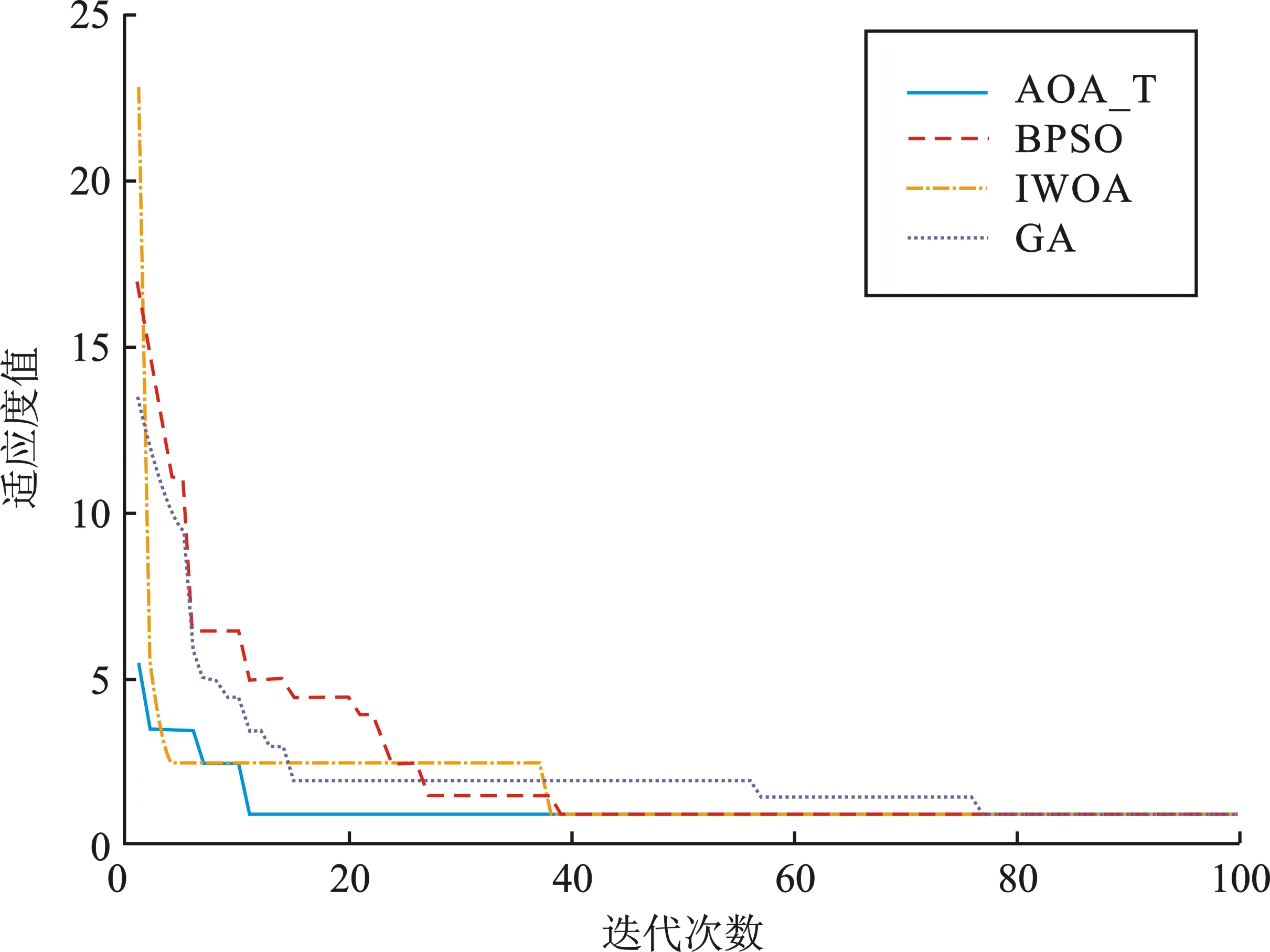
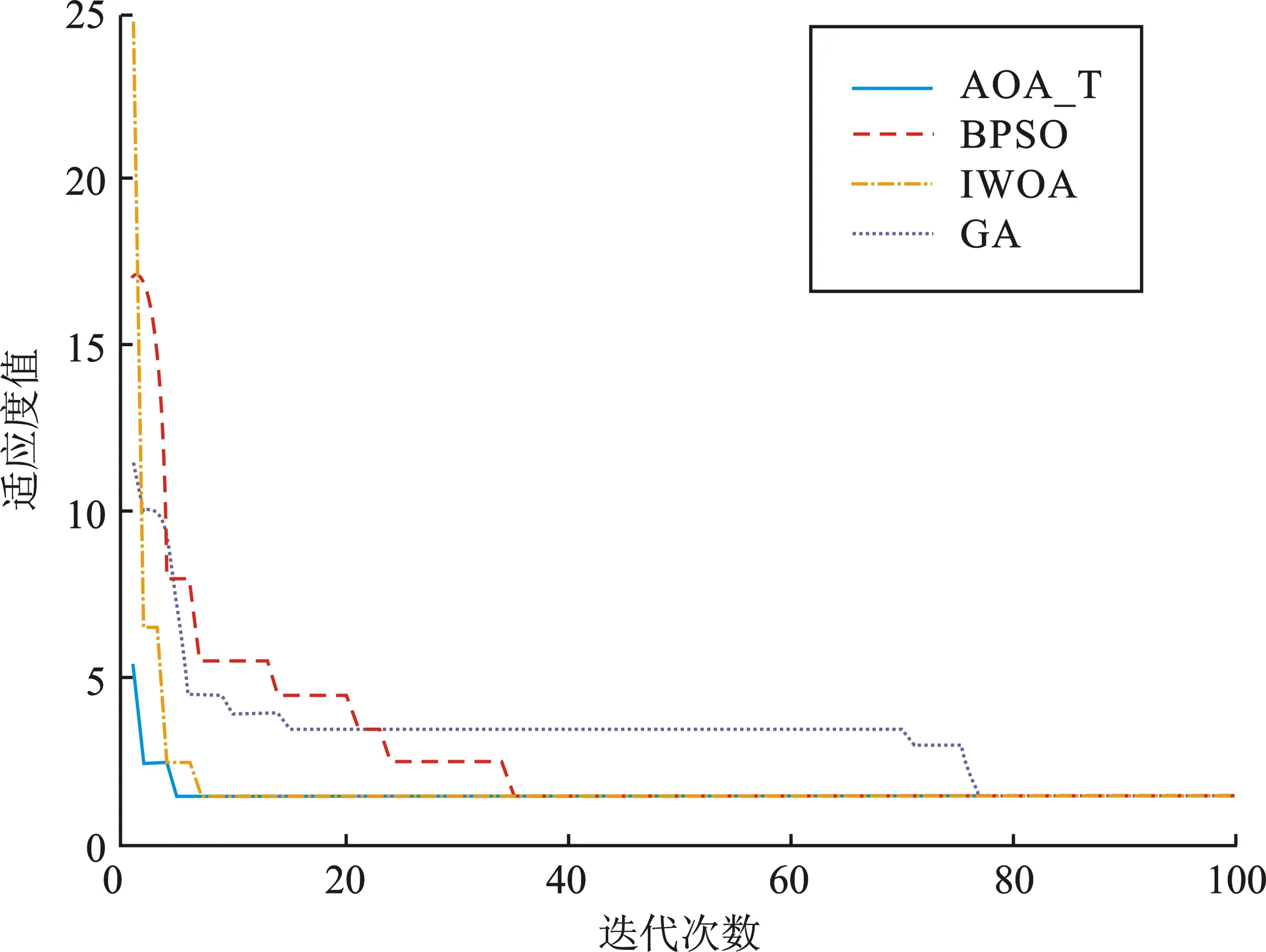
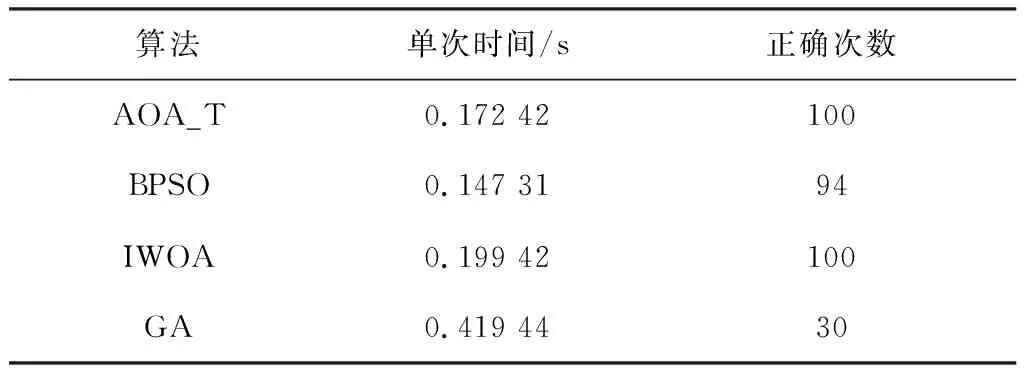
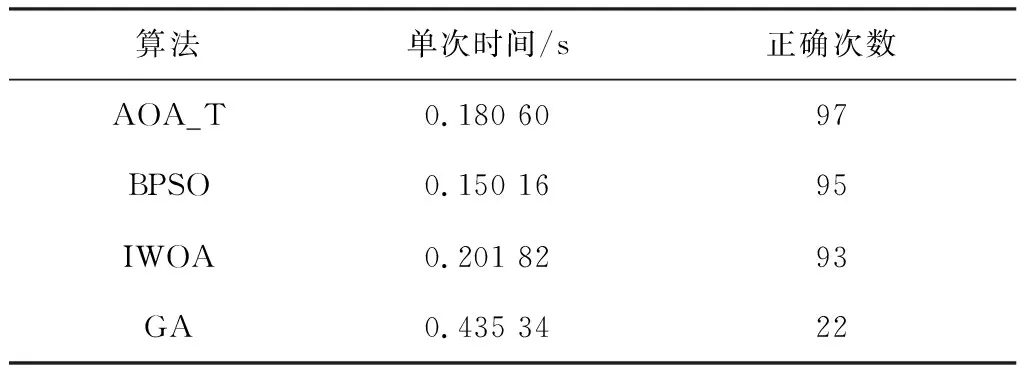
式中,C为当前迭代次数;M为最大迭代次数;min为加速系数的相对最小值,该值决定了全局搜索精度,本文取0.2;max为加速系数的相对最大值,该值决定了局部搜索精度,本文取1。定义r1为服从[0,1]均匀分布的随机数,当r1>MOA时,进行勘探阶段;当r1 在后期搜索阶段中,算法又设定了一个概率系数(Math Optimizer Probability,MOP)来控制当前阶段的搜索速度,如式(6)所示。 (6) 式中,α是一个敏感参数,定义了在迭代过程中的局部搜索精度,本文中取-5。 在算法勘探阶段,通过乘法运算和除法运算实现全局寻优,定义r2为服从[0,1]均匀分布的随机数,当r2<0.5时,执行除法运算;当r2>0.5时,执行乘法运算,其位置更新如式(7)所示。 (7) 式中,xi,j(C+1)为迭代C+1次时,第i个解在第j维的位置;best(xj)为在迭代过程中最优个体xj在第j维的位置;ε为随机比例系数,防止出现分母为0的情况;μ为在调整搜索过程的控制参数;UBj和LBj分别为第j维上的搜索上、下限。 在算法开发阶段,通过加法运算和减法运算实现局部寻优,定义r3为服从[0,1]均匀分布的随机数,当r3<0.5时,执行减法运算;当r3>0.5时,执行加法运算,其位置更新如式(8)所示。 (8) 在算术优化算法中,MOA的大小取决于算法的搜索阶段,MOA越大,局部搜索精度越高;MOA越小,全局搜索精度越高。对于故障区段定位问题,需要对局部进行充分探索,因此对MOA进行变换,使其由小变大变换为由大变小,定义其为MOA_T,如式(9)所示。 (9) MOA与MOA_T的变化曲线如图2所示。 图2 MOA与MOA_T变化曲线Figure 2. MOA and MOA_T variation curves 对使用MOA_T的算术优化算法定义为AOA_T,AOA_T算法流程如图3所示。 图3 AOA_T算法流程Figure 3. Flow of the AOA_T algorithm 本文的仿真实验基于Intel(R)Core(TM)i7-10875h CPU@2.3 GHz、16 GB内存,操作系统为Windows 11,仿真软件为MATLAB 2021a。图4为IEEE33节点模型。 图4 IEEE33节点模型Figure 4. IEEE33 node model 为验证AOA_T模型的优越性,本文选取BPSO、GA和IWOA作为比较模型。AOA_T参数设置为:种群规模N=50,最大迭代次数M=100,加速系数相对最大值max=1.0,加速系数相对最小值min=0.2,控制参数μ=0.6,敏感参数α=-5,上下限为1和0。BPSO参数设置为:种群规模为50,最大迭代次数为100,速度范围为[-4,4],加速常数c1和c2均为2,惯性因子为0.9。GA参数设置为:种群规模为50,最大迭代次数为100,交叉概率为0.8,变异概率为0.01。IWOA参数设置为:种群规模N=50,最大迭代次数M=100,上下限为1和0。 对IEEE33节点配电网进行单点故障、两点故障和三点故障仿真,正确输出如表1和表2所示。 表1 故障信号无畸变定位结果 表2 故障信号有畸变定位结果 选取表1中故障点为8、31和表2中故障点为12、畸变点为7的两个故障区段定位参数,4种算法的迭代过程如图5和图6所示。 图5 故障点为8、31的4种算法迭代过程Figure 5. Iteration process of the four algorithms with fault points 8 and 31 图6 故障点为12、畸变点为7的4种算法迭代过程Figure 6. Iteration process of four algorithms with a fault point of 12 and an aberration point of 7 由图5可知,GA在迭代初期计算出的最优值下降较快,但在迭代中期易陷入局部最优状态,无法快速获得最优值,BPSO和IWOA较GA能快速跳出局部最优状态,分别在最大迭代次数为39次和38次时算出最优值,AOA_T在最大迭代次数为11次时能算出最优值。 由图6可知,当故障信号出现畸变后,GA在迭代次数为50次时仍无法跳出局部最优状态,BPSO和故障信号在无畸变时的状态表现相似,在最大迭代次数为35次时算出最优值,IWOA加入了扰动算法,因此可以在最大迭代次数为7次时就可算出最优值,AOA_T能在最大迭代次数为5次时算出最优值。 为验证准确性,本文对4种算法进行单点和两点故障的100次循环测试,测试结果如表3和表4所示。 表3 单点故障100次循环测试(故障点为29) 表4 两点故障100次循环测试(故障点为8、31) 由表3可知,在100次循环测试中,BPSO的单次计算时间为0.147 31 s,在4种算法中计算最快;AOA_T和IWOA的计算时间仅比BPSO慢0.025 11 s和0.052 11 s,计算速度也较快;GA的单次计算时间是BPSO的2.85倍。在准确度方面,BPSO的正确次数为94次,低于AOA_T和IWOA的100次;GA的正确次数仅为30次,远低于其他3种算法。 由表4可知,在100次循环测试中,BPSO的单次计算时间仍最快,为0.150 16 s;AOA_T和IWOA次之,仅慢0.030 44 s和0.051 66 s;GA在4种算法中仍最慢,单次时间是BPSO的2.89倍。在准确度方面,AOA_T的正确次数为97次,略高于BPSO和IWOA的95次和93次;GA的正确次数仅为22次,远低于其他3种算法。 综上所述,在单次计算时间方面,BPSO最快,AOA_T和IWOA次之,GA最慢;在准确度方面,AOA_T最高,IWOA和BPSO次之,GA最低。综合对比下,AOA_T性能最好。 本文针对低压配电网智能台区的配电网故障区段定位问题,引进基于算术优化算法解决方法,在单点和多点故障情况下对配电网故障区段定位进行仿真对比分析。结果表明,相比二进制粒子群算法、遗传算法和改进鲸鱼算法,算术优化算法不需添加扰动算法,仅改变搜索阶段顺序就可实现故障区段定位,且算法所需的迭代次数更少,收敛速度更快,准确度更高。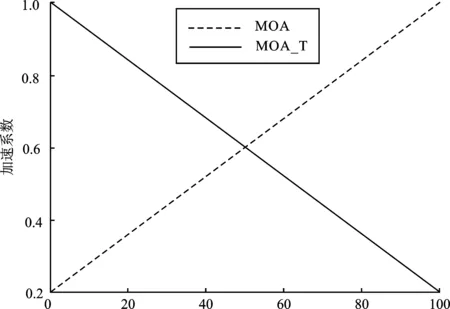

3 仿真实验


4 结束语

