基于实物期权的高速铁路建设时机分析*

陈佩虹 卢 媛 陈 娟

(北京交通大学经济管理学院,100044,北京∥第一作者,副教授)

高速铁路(以下简称“高铁”)具有显著的经济社会效益,同时也具有建设难度大、建设期长、投资额巨大的特点,因此其成本与收益随时间增加存在极大的不确定性。传统的项目评估体系所使用的净现值法无法解释这种不确定性,因而使得项目决策者在选择高铁建设时机时充满挑战。特别是在一些欠发达地区,过早投资建设高铁可能面临沉重的还贷与运营补贴压力,加剧债务问题。若在高铁项目评估体系中增加对投资时机的评估将使项目评估更加全面,有利于提高投资可靠性,降低决策风险。实物期权可以用于评估这种不确定性因素的影响。

1 高铁项目建设时机选择的理论分析与建模

1.1 期权类型识别

1.1.1 实物期权

实物期权的标的物是各种实物资产。在实物期权中,有效期称为投资机会消失的时点,即在某一时刻决策者丧失了投资机会。这个期限并不像金融期权合约中规定的十分具体的期限,但一般情况下,实物期权的期限较金融期权的而言更长。行权价格在实物期权中表现为不可逆转的投资成本,即决策者必须付出的资金成本。另外,类似于股票价格会有波动性,在投资机会消失之前,项目价值也会受到多种因素影响而具有波动性。因此,项目的预期现金流净现值也会随之发生变化。

实物期权有多种类型,例如放弃期权、扩张期权、收缩期权、转换期权、延迟期权和增长期权等。从国家角度来看,对一个具有不可逆性的项目投入资源,不仅需考虑它所带来的预期效益,还应看到这些投资机会中所隐含的期权价值。对一个项目进行最优设计与决策是政府科学发展战略的本质体现[1]。

1.1.2 高铁项目的投资特性

1) 不确定性和风险性。高铁项目在规划建设阶段和开通运营阶段存在着诸多不确定性和风险性。规划建设阶段的不确定性主要是高昂的资金成本和时间成本等,项目开通运营阶段的不确定性主要是对高铁项目效益有重要影响的客运需求、运输价格、VOT(旅行时间节省价值)等的变化,这些不确定性会带来项目投资风险。因此高铁项目适用于引入实物期权进行评价。依据实物期权应用框架,首先应对高铁项目投资决策中的期权类型进行识别。识别可分别从规划建设和开通运营两个阶段展开。对于每个阶段,基于高铁项目投资的风险性,获得与决策机会相关的成本、收益和不确定性的初步估计。

2) 期权类型识别。根据以上对不确定性的分析,可以识别出高铁项目规划建设的期权类型有延迟期权和增长期权,开通运营阶段中的期权类型有扩张期权、转换期权和放弃期权。

(1) 延迟期权:对应着建设时机。若时机恰当,可以选择及时展开项目;若时机尚早,则新线建设暂缓。

(2) 增长期权:早期建设中预留线和提速空间的设计是后续能力扩张的先决条件,可以打开未来客流增长机会。

(3) 扩张期权:经济社会发展情况乐观,运量增加,则存在扩张期权。

(4) 转换期权:一些高铁客流不足时,可以转而发展高铁货运业务,则存在转换期权。

(5) 放弃期权:由于资产专用性较强,在高铁项目中放弃期权价值很低。

本文以建设时机为研究主题,因此重点关注高铁项目规划设计中的延迟期权。

1.2 不确定性因素影响函数

为求解高铁项目规划设计中的延迟期权,需对主要涉及的不确定性因素进行建模分析。本文选择的不确定性因素为项目的建设成本和运营效益。由于客流量和VOT值是影响运营效益的最主要因素,所以本文主要对客流量、VOT值和建设成本进行分析。

1.2.1 客流量的建设时机影响函数

项目建设成本和运营效益服从几何布朗运动是实物期权模型常用的假设之一[2]。几何布朗运动是交通运输研究中一种常用的随机过程,适用于人口、铁路需求和公路需求等的不确定性[3]。本文用几何布朗运动来描述高铁项目客流量的变化。

研究高铁项目投资建设时机涉及到项目建设年限和项目运营年限。假设项目建设完工需要时间(年)为TC,运营时间(年)为N。用i表示开始建设高铁项目后的第i年,则i∈[0,TC+N]。此时引入高铁项目建设时机变量t(t≥0)(单位,年),当t=0时,表示项目按期建设;当t>0时,表示项目推迟建设。设T=t+i,则T∈[t,t+TC+N]。

考虑不确定因素的影响,高铁项目客流量可表示为:

Q(T)=Qifq(t)

(1)

式中:

Qi——可行性研究中项目开始建设后第i年客流量的原预测值,为确定值;

fq(t)——客流量的建设时机影响函数;

Q(T)——客流量新预测值,表示在建设时机影响下新的客流量值。

类比股票价格随机波动的几何布朗运动,高铁项目客流量Q(T)的几何布朗运动微分方程表示为:

dQ(T)/Q(T)=μqdT+σqdB

(2)

式中:

μq——客流量的漂移率,反映高铁项目客流量的发展趋势;

σq——波动率,表示标准差;

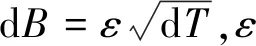
由Q(T)服从几何布朗运动,可以推导出客流量的建设时机影响函数fq(t)也服从几何布朗运动。设布朗运动函数为B(t),即:

dfq(t)=μqfq(t)dt+σqfq(t)dB(t)

(3)

根据伊藤引理求得:

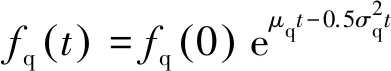
(4)

其中,fq(0)=1,表示项目按期建设时,客流量是其原预测值。

一般而言,随着经济社会的快速发展以及城市化率的不断提高,居民出行距离会不断增加,支付能力不断提升,表明推迟投资在很大程度上会有利于客流量的增加,由此可知,μq>0。

1.2.2 VOT值的建设时机影响函数

基于VOT值对于交通运输领域研究的重要意义,国内外在其经验估计方面做出了巨大努力。例如荷兰采用陈述性偏好数据估计出行者效用函数来研究VOT,日本在铁路项目评估中采用收入逼近法来估计VOT值。根据《铁路建设项目经济评价方法与参数》中的方法估算VOT值[4],如式(5)所示。

Vi=ωi/[(365×5/7-11)×8]

(5)

式中:

Vi——第i年VOT原始值,单位 元/h;

ωi——第i年城镇居民人均可支配收入,单位 元。

当项目推迟建设时,社会经济的发展会影响沿线居民的收入,进而改变旅客对节省时间的支付意愿。通常来说,VOT值随时间发展与居民收入保持同方向变化,即:

V(T)=VifV(t)

(6)

式中:

V(T)——VOT新值;

fV(t)——VOT值的建设时机影响函数。

设沿线区域城镇居民人均可支配收入的平均增长率为r,假设VOT值每年以r的比例增长,则

fV(t)=(1+r)t

(7)

1.2.3 建设成本的建设时机影响函数

当项目推迟建设时,经济与社会发展会对高铁项目建设成本有较大影响。建设成本会受项目征地拆迁、建筑材料、技术更新和劳动力费用等因素影响而具有不确定性,不过总体成本呈现上升趋势。建设成本新预测值计算公式如式(8)所示。

C(T)=Cifc(t)

(8)

式中:

C(T)——第i年建设成本新预测值;

Ci——建设成本原预测值;

fc(t)——建设成本的建设时机影响函数。

我国铁路项目中设定物价上涨预留费为3%[2],因此本文假设建设成本每年以3%的比例增长,则:

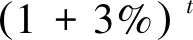
(9)

1.3 建设时机选择的实物期权模型

建设项目运营收入、运营成本和旅行时间节省效益均受到客流量影响,它们的新预测值取决于建设时机t。高铁项目的经济净现值HNPV(t)为:

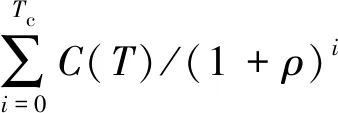
(10)

式中:

P(T)——运营收入新预测值;

S(T)——旅行时间节省效益新预测值;

O(T)——运营成本新预测值;

ρ——社会折现率。

以经济净现值最大值,即以HNPVmax(t)为目标对应的建设时机为最佳建设时机tzj。若tzj=0,则按期建设项目就是最优选择;若tzj>0时,则推迟tzj年建设是最优选择。由此可知,tzj可以从经济角度反映出该高铁项目的发展时机,为建设时机的选择提供一定的理论依据。

1.4 蒙特卡洛模拟近似求解

利用Crystal Ball软件的OptQuest优化工具可以实现蒙特卡洛模拟,具体步骤为:①按照净现值的公式建立模型。②定义决策变量、假设变量和目标变量:决策变量为建设时机t;假设变量为建设成本C(T),按固定比例上涨;客流量Q(T)服从正态分布;VOT值按固定比例上涨;目标变量为项目净现值。③ 运行OptQuest优化工具进行随机优化,得出净现值最大化条件下的最佳建设时机,以及净现值的概率分布图表。

2 基于实物期权的高铁项目建设时机分析

2.1 数据来源及相关参数设定

以高铁项目A为例进行分析。A的建设成本原预测值和客流量原预测值依据项目可行性研究可得。利用实物期权求解高铁项目A最佳建设时机建立在传统净现值法分析基础之上,因此一些基本参数取值与其保持一致,例如:μq以客流量原预测值的年均增长率来表示;σq以客流量原预测值的标准差表示;客流量波动系数kq按参考文献[2]取值;建设成本上涨率按照3%的物价上涨预留费设定;VOT值增长率参考城镇居民人均可支配收入增长率,设定为8%。各参数的取值如表1所示。

表1 高铁项目A建设时机分析参数取值

2.2 最佳建设时机求解结果

在Crystal Ball软件中设定好决策变量、假设变量以及目标变量,根据该软件计算的高铁项目A净现值概率如图1所示。

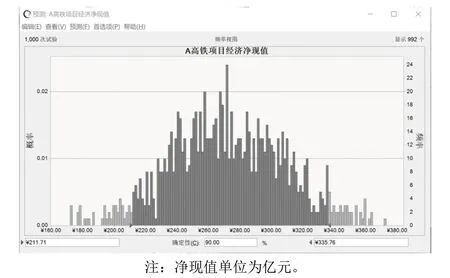
图1 高铁项目A净现值概率分布截图

取0≤t≤30,在该设定时间范围内对变量变化趋势进行1 000次模拟,得到高铁项目A的最佳建设时机为18年,经济净现值最大值为271.81亿元(采用传统方法计算的经济净现值为-643.78亿元)。经济净现值以90%的概率分布在211.71亿元和335.76亿元之间。

除了按照式(10)计算得出经济净现值外,本文还基于实物期权模型考虑了财务净现值最大化,即忽略旅行时间节省效益,仅考虑建设成本、运营成本和运营收入。此时,最佳建设时机为25年,财务净现值为78.72亿元(采用传统方法计算的财务净现值为-1 199.60亿元)。由此可以看出,当不考虑旅行时间节省效益时,建设时机将进一步推迟。

2.3 敏感性分析结果

实物期权的价值与投资机会消失之前项目价值的波动性密切相关。在高铁项目中,客流量的波动性通过影响运营收入、运营成本和旅行时间节省效益间接影响到项目价值。因此,本文主要对σq进行敏感性分析,分别运行Crystal Ball软件并记录该值在上下20%范围内波动时对项目经济净现值最大值以及建设时机的影响。敏感性分析结果如表2所示。

表2 高铁项目A敏感性分析

由表2可见,当客运量波动率增加时,经济净现值最大值呈现出逐渐减小的趋势;当客运量波动率减小时,经济净现值最大值呈现出逐渐增大的趋势。同时可以得出,σq波动对经济净现值的影响总体而言并不明显,求解结果相对稳定,模型较为可靠。

2.4 结果分析

引入实物期权求解高铁项目A建设时机时只考虑了该项目的建设成本、运营成本、运营收入和旅行时间节省效益,计算结果得出高铁项目A尚未处在最佳建设时机,推迟18年建设将会达到最优净现值。该项目建在地广人稀、经济发展迟滞的西北地区,是我国政府决策部门从国家整体利益和长远发展战略出发做出的一项部署。除了经济效益以外,更多考虑了该项目的社会效益,可以说,社会效益是这一项目启动的最重要依据。

3 结语

高铁项目评价应是一个动态优化的过程,项目成本与收益随时间增加存在极大的不确定性。实物期权提供了一种衡量和估计这种不确定性的框架,可以增强高铁项目建设时机考察的理论支撑,使项目评价更加客观全面,使评价结果更有参考价值,使高铁项目评估的系统性得到进一步提升。