基于CoppeliaSim的UR5机器人码垛仿真

黄 伟,闵柏成,张世超

(中国船舶集团有限公司第七二三研究所,江苏 扬州 225101)

0 引 言

使用机器人替代一些传统的制造产业是实现制造强国的必要途径[1-3],机器人建模与仿真技术已成为研究机器人的一个不可或缺的途径。目前机器人仿真软件常见的有RobotStudio、RoboGuide等,但这些软件需要昂贵的价格和后续使用价格。三维软件如UG、PROE等虽然可以进行仿真,但是其扩展性差[4]。OpenGL图形库功能强大,但需大量软件开发工作才能用于机器人建模和仿真。Matlab机器人工具箱的仿真显示效果比较差,难以进行逼真的仿真。CoppeliaSim仿真软件可以将三维软件里面的精确模型导入其中进行仿真,还可以联合Python、Matlab等软件进行联合仿真[5]。利用Matlab的矩阵计算优势,结合CoppeliaSim仿真软件进行联合仿真,可以建立多种机器人工作环境,并可以快速进行运动学解算[6]。

1 机器人模型的建立

在CoppeliaSim仿真平台中进行机器人的模型建立,先通过三维软件(例如UG、PROE等)画出机器人各个部件的三维信息,然后将其转化成stl格式的文件;其次在CoppeliaSim仿真平台中导入这些文件,即可以看到各个部件在CoppeliaSim软件界面上;最后在CoppeliaSim软件中添加相关关节的位置姿态信息,将各个导入的机器人部件附属在各个关节上,建立好机器人各系统的树形结构,附属好关节的部件就会随着机器人关节的旋转进行相应的跟随运动。图1(a)为在CoppeliaSim中建立的UR5模型,图1(b)为在CoppeliaSim中建立的树形结构图。整个流程如图2所示。

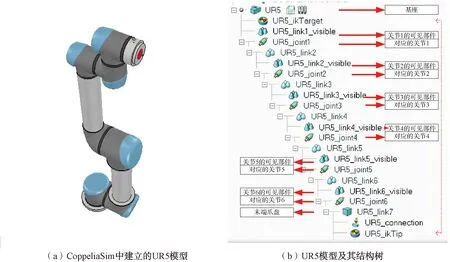
图1 CoppeliaSim中建立的UR5模型及其结构树

图2 CoppeliaSim中建立机器人模型的流程

2 机器人运动学分析

UR5机器人为6自由度串联机器人模型,可以用标准D-H建模法对UR5进行建模。图3、图4分别为UR5结构图和其标准D-H参数坐标系图。以UR5机器人为例,由表1的参数可以进行运动学方程的推导。坐标系从{i-1}到坐标系{i}的变换矩阵可以写成:

表1 UR5型机器人的连杆参数表

图3 UR5机器人结构图

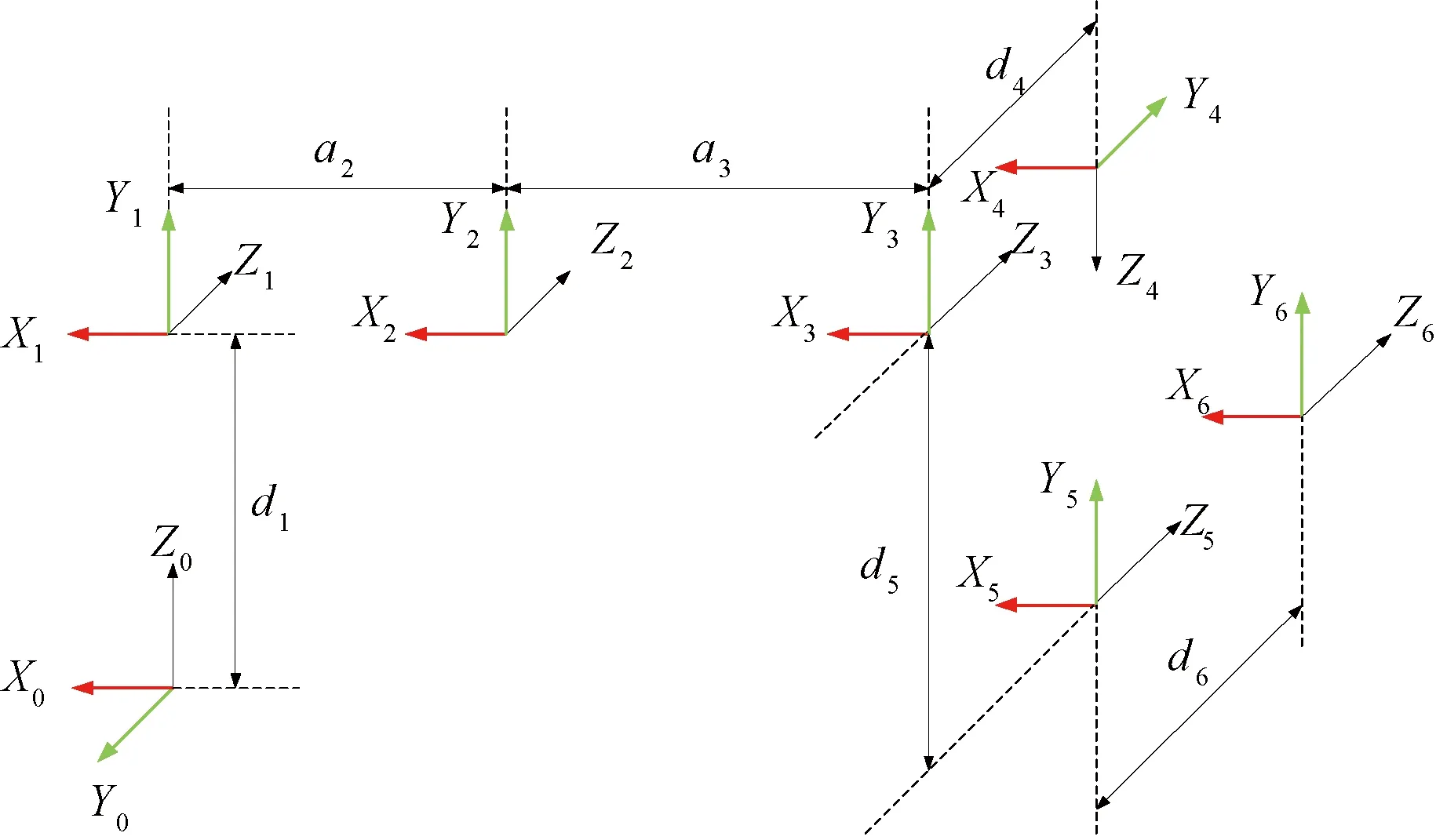
图4 UR5机器人D-H坐标系

(1)

代入表1中参数,最终变换矩阵为:

(2)

就完成了正运动学的求解。

逆运动学求解是已知变换矩阵T,求6个关节角度。逆运动学求解有解析法、迭代法,这里采用解析法求解。逆运动学算法求解的角度范围为θ∈[-π,π],因为标准的反正切arctan的值域是[-π/2,π/2],所以不能使用。使用一个改进的反正切的函数Atan2(y,x)(Matlab里有这个函数),这个反正切的求法值域也满足要求。已知最终变换矩阵:

(3)

左右变换逆乘得到:

(4)

式(4)左右侧第3行第4列对应相等,求得关节角θ1为:

(5)

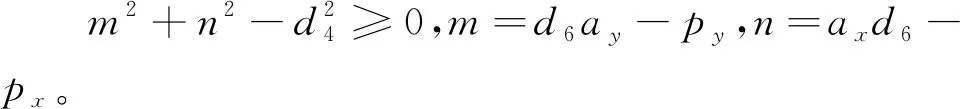
式(4)左右2侧第3行第3列对应相等,求得关节角θ5为:

θ5=±arccos(axs1-ayc1)

(6)

式中:axs1-ayc1≤1。

式(4)左右侧第3行第1列对应相等,求得关节角θ6为:

θ6=Atan2(m,n)-Atan2(s5,0)=

Atan2(m/s5,n/s5),s5≠0

(7)

左右变换逆乘得到右侧等式:

(8)

式(8)左右第1行第4列对应相等,第2行第4列对应相等,求得关节角θ3为:

(9)

式中:m2+n2≤(a2+a3)2,并有:

(10)

为了简化缩写,约定c23=cos(θ2+θ3),s23=sin(θ2+θ3)。

将式(10)展开,将θ3代入式(10),求得关节角θ2为:

θ2=Atan2(s2,c2)

(11)

约定s6=sinθ6,c6=cosθ6,式(8)左右第1行第2列对应相等,第2行第2列对应相等,求得关节角:

θ4=Atan2(-s6(nxc1+nys1)-c6(oxc1+oys1),

ozc6+nzs6)-θ2-θ3

(12)

假设6个关节角都取1°,经Matlab编程验证得出末端位置姿态矩阵T。将得出的末端位置姿态矩阵在Matlab中代入逆运动学求解,得出8组逆解,其中一组为6个关节角,都是1°,从而验证了运动学公式的正确性。

3 机器人码垛环境坐标系之间的关系

机器人完成码垛作业需要知道搬运起始点和最终点的机器人末端位置和姿态。以UR5机器人为例,搬运长方体如图5所示,UR5机器人搬运过程中,用末端手爪工具从传送带抓取物件,然后放置在指定的位置。

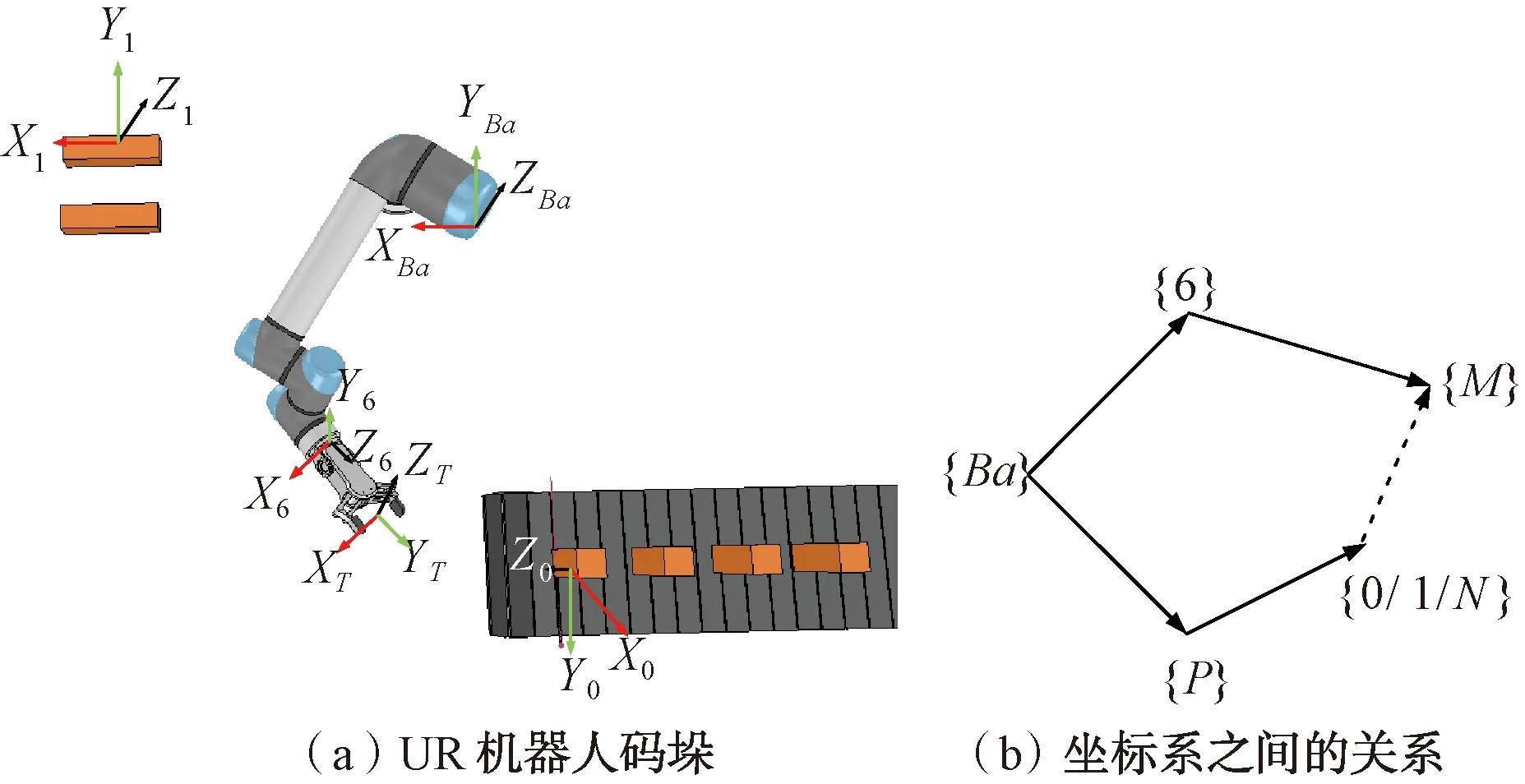
图5 UR机器人码垛及其坐标系之间的关系

图5中{Ba}代表UR5基座坐标系;{6}代表UR5机器人末端坐标系;{M}代表UR5手爪工具坐标系;{0}代表起始抓取点坐标系;{1}代表搬运结束点的坐标系;{N}代表搬运过程中点的坐标系。各个坐标系关系组成一个闭环链如图5(b),各个坐标系关系如下:

(13)

等式两边同乘以逆矩阵得:

(14)

式(14)给出了UR5机器人末端夹持工具沿给定轨迹运动时,机器人的运动学方程。除了{6}系相对于{Ba}系的位置和姿态在变动中不确定之外,其余的位姿都是预先规定好的,求出UR5码垛运动轨迹上各个目标轨迹点处{6}系相对于{B}系的位姿,就完成了工件坐标系到机器人坐标系的转换。

完成工件坐标系到机器人坐标系的转换后,根据机器人运动学解算就可以求出机器人码垛运动到各个轨迹点处所对应的机器人的各个关节角。

首先每组解对应关节角度值应该符合机器人手册里规定的关节角取值范围。其次从满足关节角运动范围的解集中选择关节角绝对值之和最小的解,最小的解即是波动范围最低的解,也是最合适的解。

求得的运动学反解往往不唯一,须根据机器人的各项参数和工作环境,从中选择最合适的解[7]。

此关节角数据是在Matlab中计算生成的,并以弧度值的形式保存成文本格式,此文本可以用来提供给CoppeliaSim进行仿真。

4 基于CoppeliaSim的UR5机器人仿真运动

CoppeliaSim软件的运动仿真可以在建立好模型和场景的基础上,通过对模型添加相应的脚本语言进行运动学和动力学控制,但是其不能进行位置姿态计算,也不能进行复杂的矩阵计算。机器人运动学动力学涉及到很多矩阵方面的知识,所以需要结合C、MATLAB、Python等语言进行矩阵运算,然后将运算结果提供给CoppeliaSim软件进行仿真。本文的UR5机器人需要将4个长方体运送到指定位置,初始和最终长方体码垛结束后的位置如图6所示。

图6 初始和最终长方体码垛结束后的位置

本文用Matlab解算逆运动学生成UR5机器人进行码垛运动所需的关节角,然后将关节角参数传给CoppeliaSim软件控制机器人进行运动。在CoppeliaSim软件中添加脚本程序调用相应函数来控制机器人关节、传送带、手爪,具体参考CoppeliaSim中菜单栏的使用说明。当传送带将长方体传送到指定位置时自动停止传动,相同的长方体都传送到相同的位置停止。长方体被送到传送带上指定的位置后,机器人通过控制各个关节的转角让手爪到指定位置进行抓取,靠近长方体时通过脚本程序设定夹住物块,然后将长方体搬移至指定的位置上。重复上述操作,将所有长方体放置在相应的位置上,就完成了码垛作业。

整个过程如图7所示:(1)传送带送到指定位置;(2)UR5机器人移动到手爪夹取位置;(3)机器人进行装夹;(4)机器人搬运到指定位置;(5)机器人夹具松开,机器人移动回原点;(6)重复上述5个步骤,将不同的长方体物块放置在指定位置。

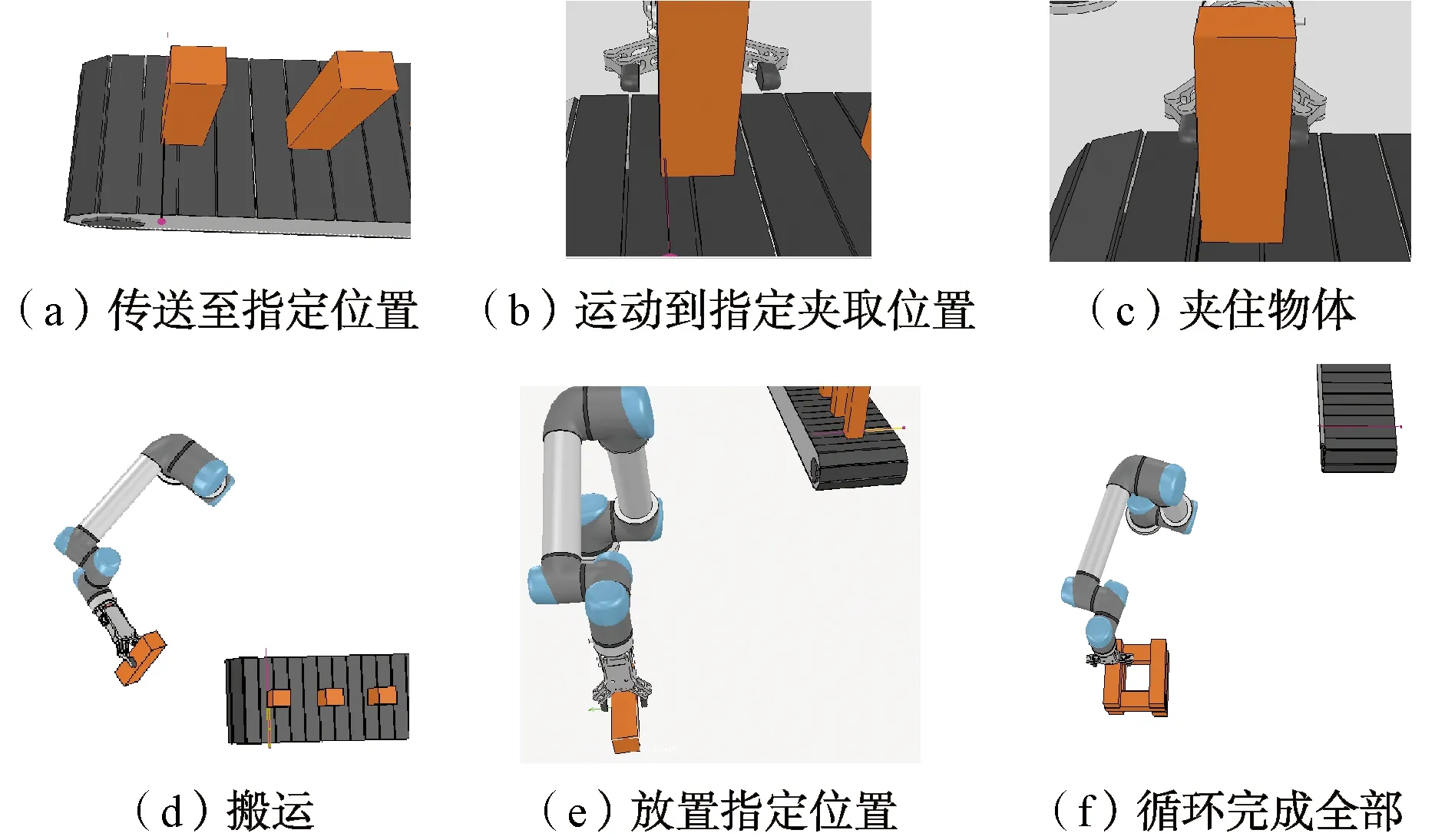
图7 机器人码垛过程

5 结束语

采用本文方法对UR5机器人码垛过程进行了仿真。在CoppeliaSim中建立了机器人及码垛作业环境的三维模型,对UR5机器人进行运动学分析并在Matlab中计算获取了码垛过程中的机器人各个关节的转角轨迹,将Matlab生成的转角信息传递给CoppeliaSim,在CoppeliaSim软件仿真平台中对码垛作业过程进行了运动仿真。仿真结果表明,所提方法能够生成无干涉码垛运动轨迹和正确的机器人在运动中的各个转角参数。本文方法可以运用到其它机器人仿真中。