基于能量法的高频冲击载荷下机械结构振动特性研究

李征宇,王 薇,陈 强

(1.中国船舶集团有限公司第七二三研究所,江苏 扬州 225000;2.东南大学,江苏 南京 211189)

0 引 言

船舶、高速列车、航空航天等领域的机械结构在服役过程中不可避免地面临冲击载荷的作用。冲击载荷是结构服役时面临的最恶劣力学环境之一[1-4],通常具有短时瞬态、宽频带和高量级等超常特性。极端的冲击载荷对电子仪器等冲击敏感元件的破坏作用十分突出,极大影响了机械结构的正常工作,严重时可导致结构发生失效。因此,在机械结构设计过程中必须重视冲击问题。

冲击载荷作用下,结构时域响应的精确预示对结构设计和安全性能评估具有重要意义。但由于冲击载荷具有作用时间短、频带范围宽和载荷量级高等复杂特性,采用有限元、边界元等离散化方法分析宽频段的瞬态冲击问题时,需要划分大量的网格,使得计算模型规模很大、计算分析效率极低。此时,选择能量法来预示结构瞬态冲击响应具有较高的计算效率。

统计能量分析(SEA)通过将结构划分为若干子系统,将结构的振动能量在空间和频域内进行平均,进而建立子系统间的能量传递方程,并获取结构振动特性[5]。由于SEA方法具有极高的计算效率和较好的分析精度,在航空、航天、船舶、建筑等领域有着广泛应用。传统的SEA方法通常用于分析频域内的高频动力学问题。近年来随着SEA相关理论的发展,SEA方法逐渐拓展到时域动力学问题的分析,极大地扩展了SEA方法的应用范围。

基于SEA理论发展的时域动力学分析方法主要有瞬态统计能量分析(TSEA)[6-9]和瞬态局部能量分析(TLEA)[10-11]2种。在理论研究方面,丁少春等[9]基于TSEA 方法研究了耦合强度对两自由度系统瞬态能量响应的峰值时间和峰值能量的影响规律,进而评估了TSEA方法的适用范围;Guasch等[10]为解决传统差分方法的鲁棒性问题,提出了一种局部时间步进有限差分方法,提高了TSEA方法的计算精度和稳定性;Sui等[11]对比了TLEA和TSEA 2种方法的准确性,并讨论了子系统耦合强度对能量峰值分析结果的影响规律;仝宗凯等[12]考虑热效应对统计能量分析参数的影响,基于TLEA方法研究了变温环境下结构高频瞬态能量响应,分析了温度对结构能量响应的影响规律。在工程应用方面:Robinson等[13]采用TSEA方法分析了瞬态冲击载荷下建筑结构地板的振动响应和室内的声压响应,并通过试验研究验证了方法的准确性;聂旭涛等[14]对空空导弹进行了简化建模,并基于TSEA方法预示了其舱内的动力学环境,仿真结果与实测数据的对比表明TSEA方法能够较为准确地预示结构中高频动力学环境。Chen等[15]将TLEA方法与商业统计能量分析软件相结合,分析了瞬态冲击载荷下复杂整流罩结构的声固耦合响应,并分析了耦合强度对冲击响应的影响规律。

现有瞬态能量响应预示研究大多是基于TSEA方法开展的,预示结构时域冲击能量响应的精度较低。本文基于TLEA理论,给出一种机械结构时域冲击响应高精度预示方法。首先,介绍TLEA方法中控制方程、算法优势等理论基础;随后,以双振子模型和L型折板结构为例开展瞬态冲击载荷下系统的振动响应预示研究,分析对比TSEA方法和TLEA方法的预示结果,研究耦合强度对响应峰值时间和峰值能量的影响。

1 理论基础

TLEA方法是SEA方法在时域响应分析中的延伸,TLEA方法中关于能量流动的基本假定为:

e(s,t)=e+(s,t)+e-(s,t)

(1)

I(s,t)=I+(s,t)+I-(s,t)

(2)

I(s,t)=I+(s,t)+I-(s,t)

(3)

式中:e+(s,t) 和e-(s,t)分别为向左和向右的能量密度;I+(s,t) 和I-(s,t)为输入和输出的能量流;c为能量流动速度,在均匀阻尼的介质中等于波传播的速度。

对于非受载区域,其局部功率流平衡方程可表示为:

(4)

式中:Pd为阻尼所耗散的功率,其能量耗散量为:

Pd=ηωe(s,t)

(5)

式中:η为阻尼损耗因子。

将式(1)～式(3)和式(5)代入式(4)中可得:

(6)

将式 (4)和式 (6)分别对时间和空间进行微分可得:

(7)

(8)

用式 (7)减去式 (8)可得:

(9)

将∂I(s,t)/∂s的表达式代入式 (9)可得TLEA方法中的能量密度平衡方程:

(ηω)2e(s,t)=0

(10)

式 (10)中给出的是能量密度的平衡方程,但SEA方法中大多采用能量对子系统的响应进行表征。因此,需要将式 (10)对子系统的体积进行积分,进而可得:

(11)

进而,可得子系统i的功率流平衡方程为:

(12)

对于SEA系统而言,其功率流平衡方程可表示为二阶常微分方程:

(13)

对于由2个子系统组成的结构而言,其功率流平衡方程为:

(14)

(15)

对于脉冲激励作用下的系统而言,初始瞬态载荷E1(0)作用在子系统1上,而子系统2的能量、子系统1和子系统2的外部能量均为0。此时,子系统1和子系统2的瞬态能量响应表达式分别为:

(16)

(17)

进而,子系统2的瞬态能量变化率为:

(18)

当子系统2的能量变化率为0时,子系统2的能量达到峰值,则峰值时间为:

(19)

统计能量分析理论的基本假设中要求子系统间耦合强度为弱耦合。对于弱耦合工况下的结构而言,有η12/η1<<1。因此,由Taylor级数展开可得峰值时间的近似式为:

(20)

2 数值仿真

2.1 双振子模型

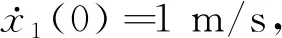
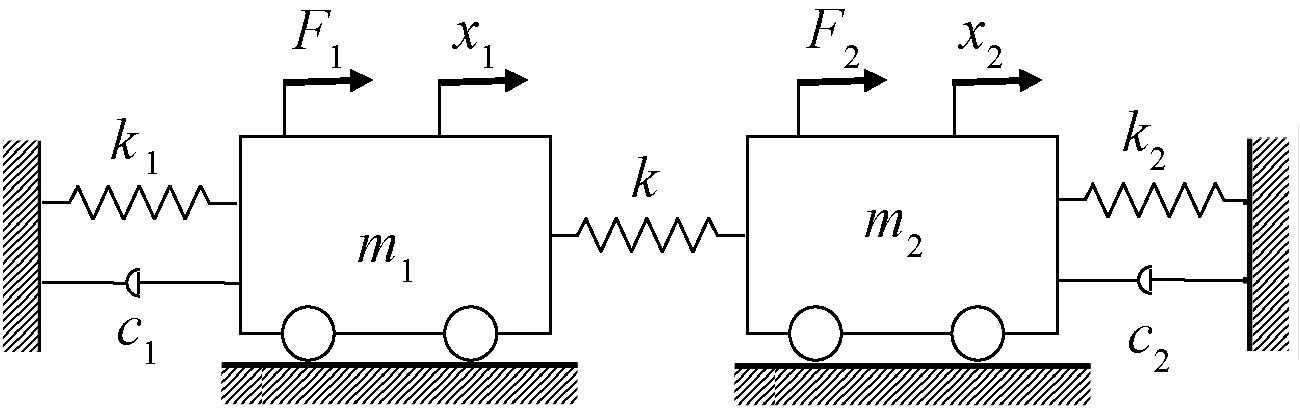
图1 双振子模型

2.1.1 精度验证

首先,对比TSEA方法和TLEA方法的预示结果,计算结果如图2所示。由图2可知,TLEA方法预示结果表明子系统1和子系统2的能量响应均呈现出周期性震荡的变化规律,而TSEA方法的预示结果在达到峰值后快速下降。这表明冲击载荷作用下各子系统的能量传播包括带有振荡特征的波动过程,这也符合结构振动特性的变化规律。子系统1和子系统2交替达到振动响应的峰值。由于结构阻尼的存在,子系统1和子系统2的能量快速衰减。此外,TSEA计算得到的峰值时间要早于TLEA方法,2种方法计算得到的峰值能量也存在一定的差异。

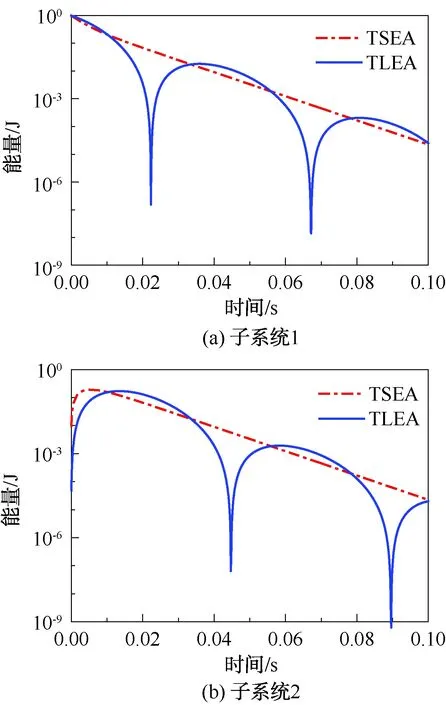
图2 子系统的瞬态能量响应

2.1.2 耦合强度的影响规律

峰值时间和峰值能量是表征瞬态冲击能量响应的重要参数。耦合强度是统计能量分析中的一个重要参数,用于表征子系统间的能量传递效率。不同耦合强度下子系统2的峰值时间和峰值能量如图3所示。计算结果表明,TLEA方法能够较好地预示不同耦合强度下子系统2的峰值时间和峰值能量,而TSEA方法的计算结果与精确解有较大差异。在弱耦合工况(耦合强度小于0.1)的条件下,TSEA方法预示得到的峰值时间约为TLEA方法的一半。随着耦合强度的增加,瞬态能量响应的峰值时间逐渐下降,而其峰值能量逐渐上升,这是因为耦合强度的增加导致了子系统间能量交换的增加和子系统能量耗散的降低。

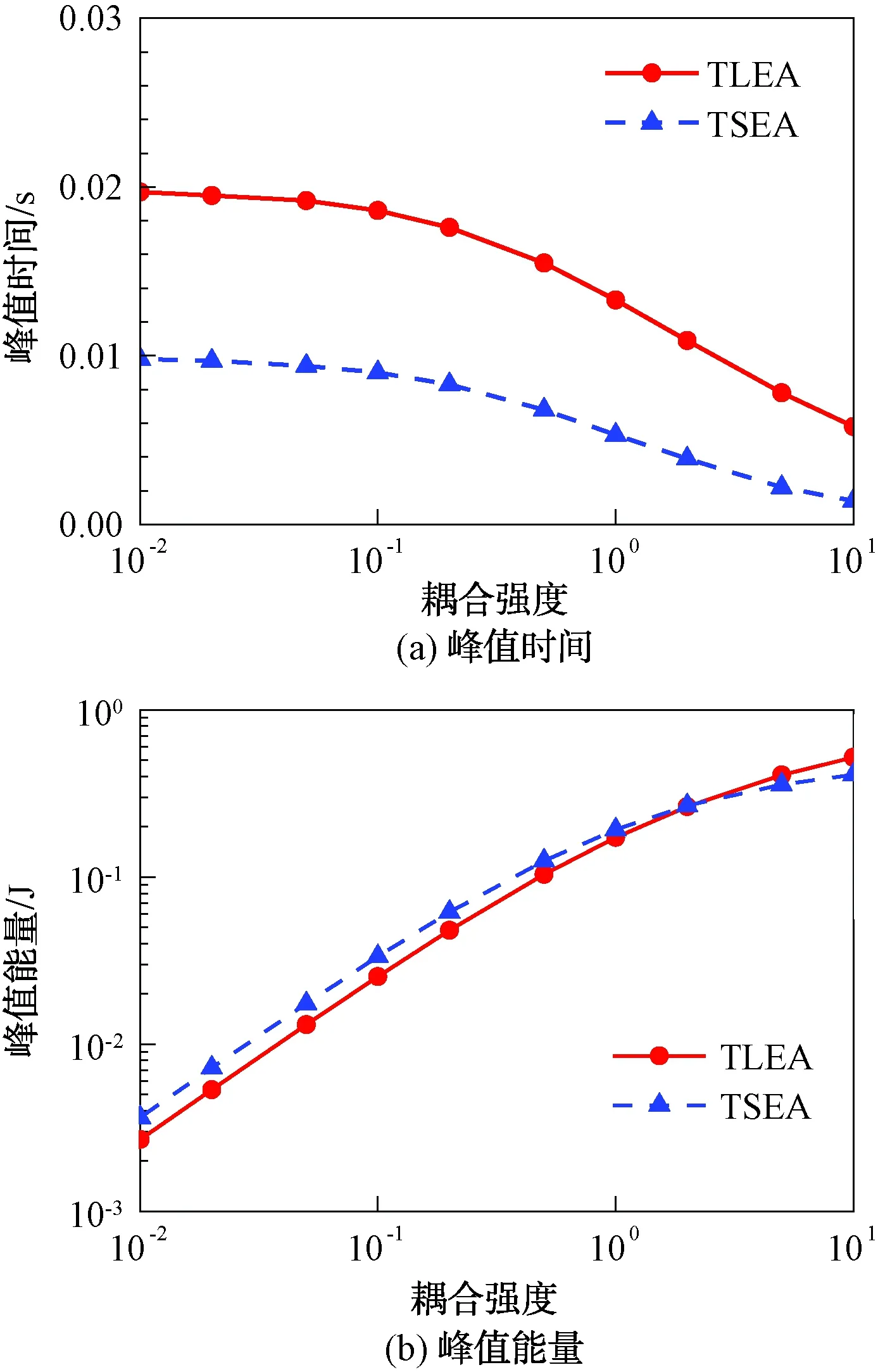
图3 耦合强度对子系统瞬态能量响应的影响

2.2 L型折板模型

本节以如图4所示的L型折板结构为例开展研究,该模型是统计能量分析理论研究中的常用模型。对板1施加均布脉冲激励,使其具有单位初始能量。将结构材料设置为TA9钛合金,分析频率设置为2 000 rad/s。系统的统计能量分析参数可由理论分析或商用软件计算获得。

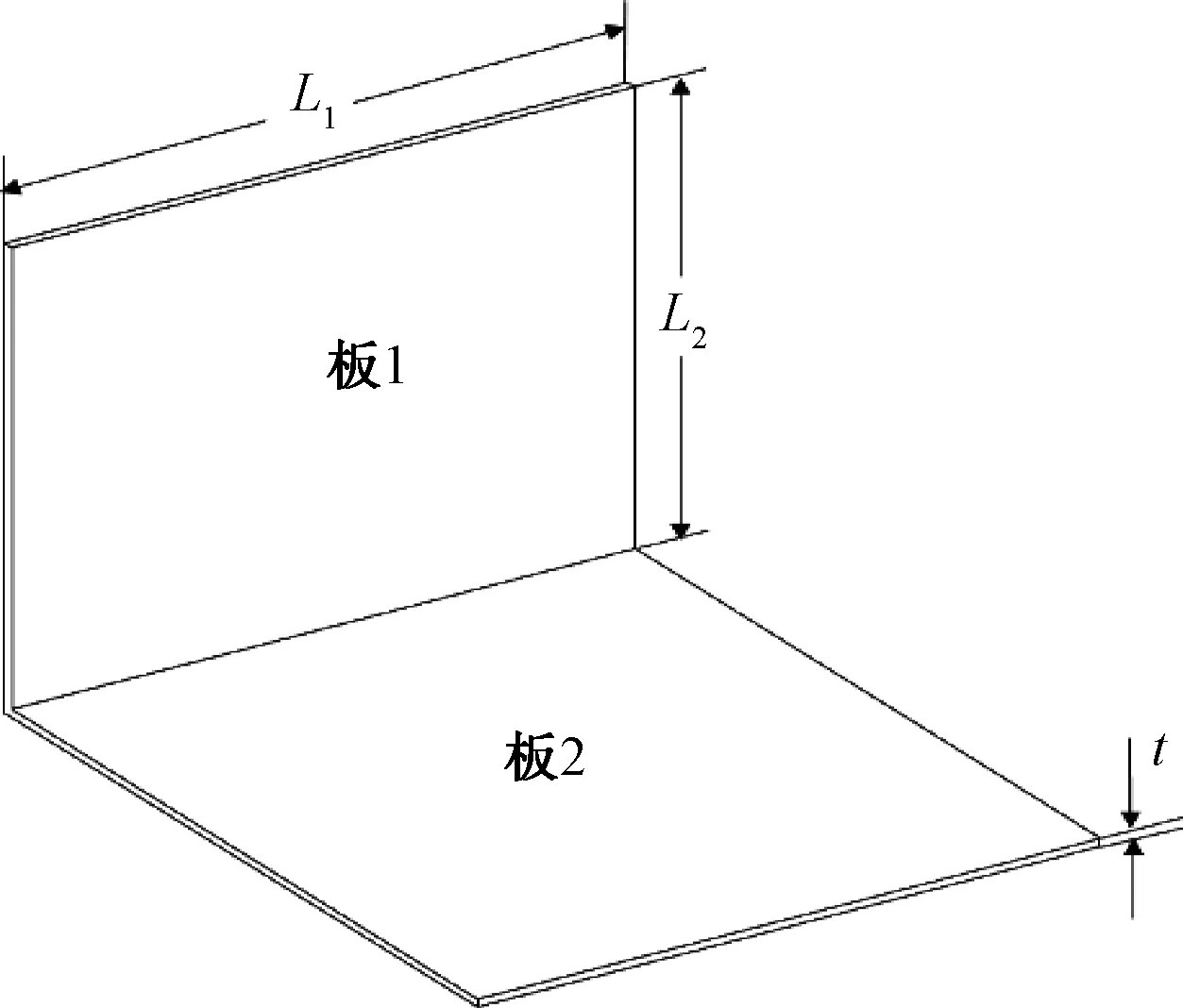
图4 L型折板

2.2.1 TSEA和TLEA的对比

为验证分析方法的准确性,本节采用有限元(FEM)方法对TSEA和TLEA方法进行对比验证。基于TSEA方法、TLEA方法和FEM方法预示得到的子系统2瞬态能量响应如图5所示。由图5所示的计算结果表明,TLEA方法分析结果与FEM方法的分析结果具有较好的一致性,能够较好地捕捉能量响应的峰值时间和峰值能量,而TSEA方法的预示偏差较大。

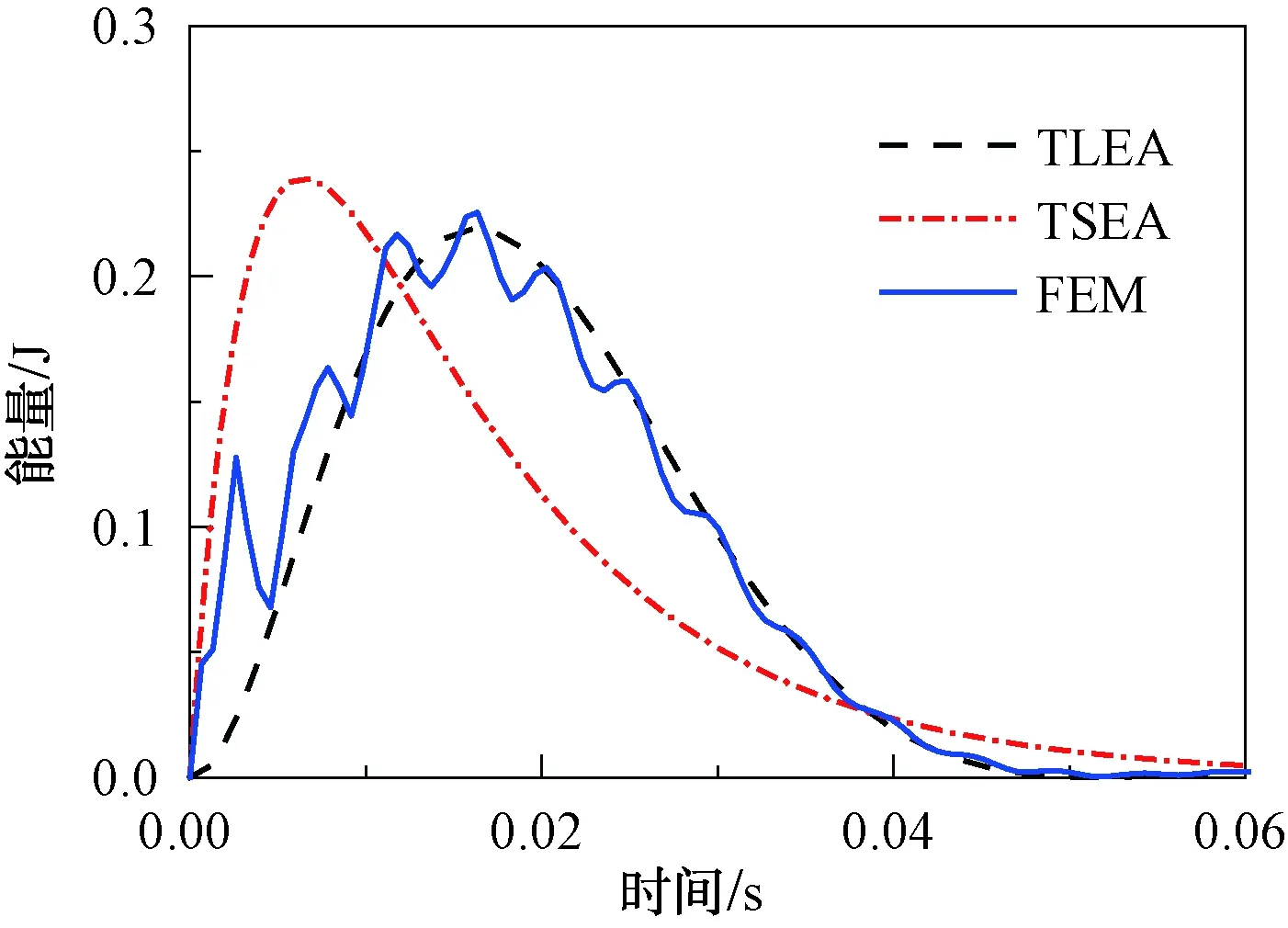
图5 板2子系统的瞬态能量响应

2.2.2 耦合强度的影响规律

不同耦合强度下板2子系统的峰值时间和峰值能量如图6所示。在耦合强度较低的工况下,子系统2能量响应的峰值时间较小、峰值能量较低。随着耦合强度的增加,子系统能量响应的峰值时间逐渐下降,而板2子系统能量响应的峰值能量逐渐上升。这是因为耦合强度的增加导致了子系统间能量交换的增加以及子系统能量耗散的降低。此外,TSEA计算得到的峰值时间要早于TLEA方法,2种方法计算得到的峰值能量也存在一定的差异。

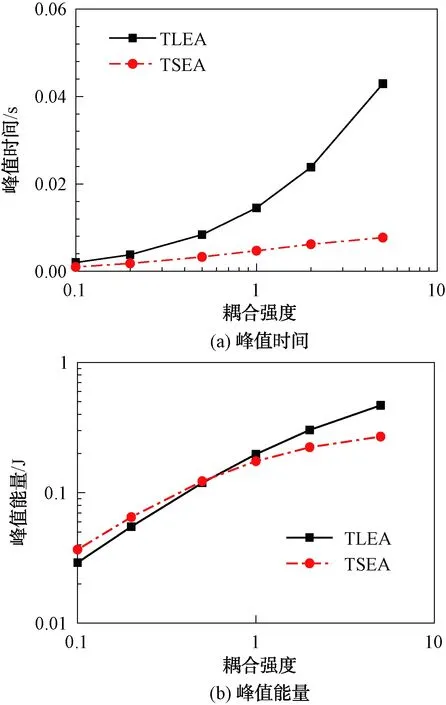
图6 耦合强度对子系统瞬态能量响应的影响

3 结束语

机械结构在服役过程中不可避免地面临冲击载荷的作用,给结构的安全性能带来了极大危害。本文针对宽频冲击载荷下结构的瞬态响应预示问题,给出了一种复杂结构瞬态能量响应的高精度预示方法。以两自由度系统和L型折板结构为例开展了数值分析,对比不同耦合强度工况下的瞬态能量响应预示结果,研究了耦合强度对峰值时间和峰值能量的影响规律。研究结果表明:TLEA方法能够精确地预示不同耦合强度下结构的瞬态能量响应。子系统冲击响应的峰值时间和峰值能量均随着耦合强度增加而降低。