声发射信号的小波阈值降噪研究
裴 嵩,孙 超
(中国船舶集团公司有限公司第七二三研究所,江苏 扬州 225101)
0 引 言
声发射技术是无损检测技术的一个分支,通过测量被测物内部材料相互作用所产生的弹性波进行故障诊断。声发射技术检测到的信号是一种非平稳信号,它在同一时刻存在多种频率成分,加之检测环境复杂,信号的噪声干扰比较大,而常规的滤波方法很难使信号和噪声有效地分离。目前,对于含有噪声的非平稳信号降噪效果比较好的方法就是小波分析法。在小波分析降噪的过程中,小波函数和阈值的选取直接影响着降噪效果的好坏。本文通过仿真声发射技术获取的信号,研究该种信号降噪过程中小波函数的选取和阈值的选取对降噪效果的影响,并比较小波降噪和小波包降噪的各自特点。
1 小波阈值降噪技术
1.1 信号在小波变换下的特征
工程上添加了高斯白噪声的非平稳信号的数学模型为:
f(t)=s(t)+n(t)
(1)
式中:s(t)为原始信号;n(t)为方差为σ2的高斯白噪声,服从N(0,σ2)分布。
对含有噪声的信号进行小波变换,将信号从时域转换到频域。Mallat在文献[1]中指出,若函数x(t)的Lipschitz指数α>0,则该函数的小波变换模的极大值将随尺度的变化成正比;若Lipschitz指数α<0,则函数的小波变换模的极大值将随尺度的变化成反比。通常信号s(t)的Lipschitz指数α>0,而白噪声n(t)的Lipschitz指数α<0,所以信号小波变换模的极大值随着尺度的增大而增大,而白噪声小波变换的模的极大值随着尺度的增大而减小。小波变换是线性的,f(t)的小波变换等于信号s(t)的小波变换和噪声n(t)的小波变换之和,所以可以在不同尺度上对变换结果进行阈值操作,以降低噪声成分,达到降噪效果。
1.2 小波阈值降噪原理和过程
原始信号经小波正交变换以后,信号对应的小波系数数目少,幅值大,包含着有用信息;噪声对应的小波系数分布均匀,数目多,幅值小,要剔除。Donoho等人根据上述现象提出了基于小波阈值的降噪方法,把幅值较小的小波系数设置为0,把幅值较大的小波系数保留或者依据某种原则进行收缩[2-3]。这样得到估计小波系数(EWC),然后利用估计出的小波系数重构信号,达到降低噪声、提高信噪比的效果。这一过程可以由以下3个步骤构成:
(1) 选择合适的小波基,对原始信号进行正交小波变换或小波包变换,得到一系列小波系数;
(2) 选择阈值,对小波系数按照一定法则进行阈值操作,得到新的小波系数;
(3) 对经过阈值操作的小波系数进行重构,得到降噪信号。
上述降噪过程如图1所示。

图1 小波降噪流程
1.2.1 小波变换和小波包变换
对采集到的离散数据进行小波分析的方法通常有2种:离散小波变换和小波包变换。小波变换的工程意义在于把信号分解成不同尺度系数的叠加,而每个尺度系数都包含有信号在一定频率范围的信息。离散小波变换是对连续小波变换尺度离散化和位移离散化的结果,其小波基函数为:
Ψj,k(t)=2-j/2Ψ(2-jt-k),j,k∈Z
(2)
离散小波变换首先选定一个尺度,再把信号和该尺度的小波函数做内积,得到一个小波系数;平移该小波函数再做内积,得到第2个小波系数;再次平移、内积,直到得到该尺度下的所有小波系数。重复上述步骤,可以得到不同尺度的小波系数,也得到了包含信号在不同频率范围内信息的一系列系数,分解示意图如图2所示。
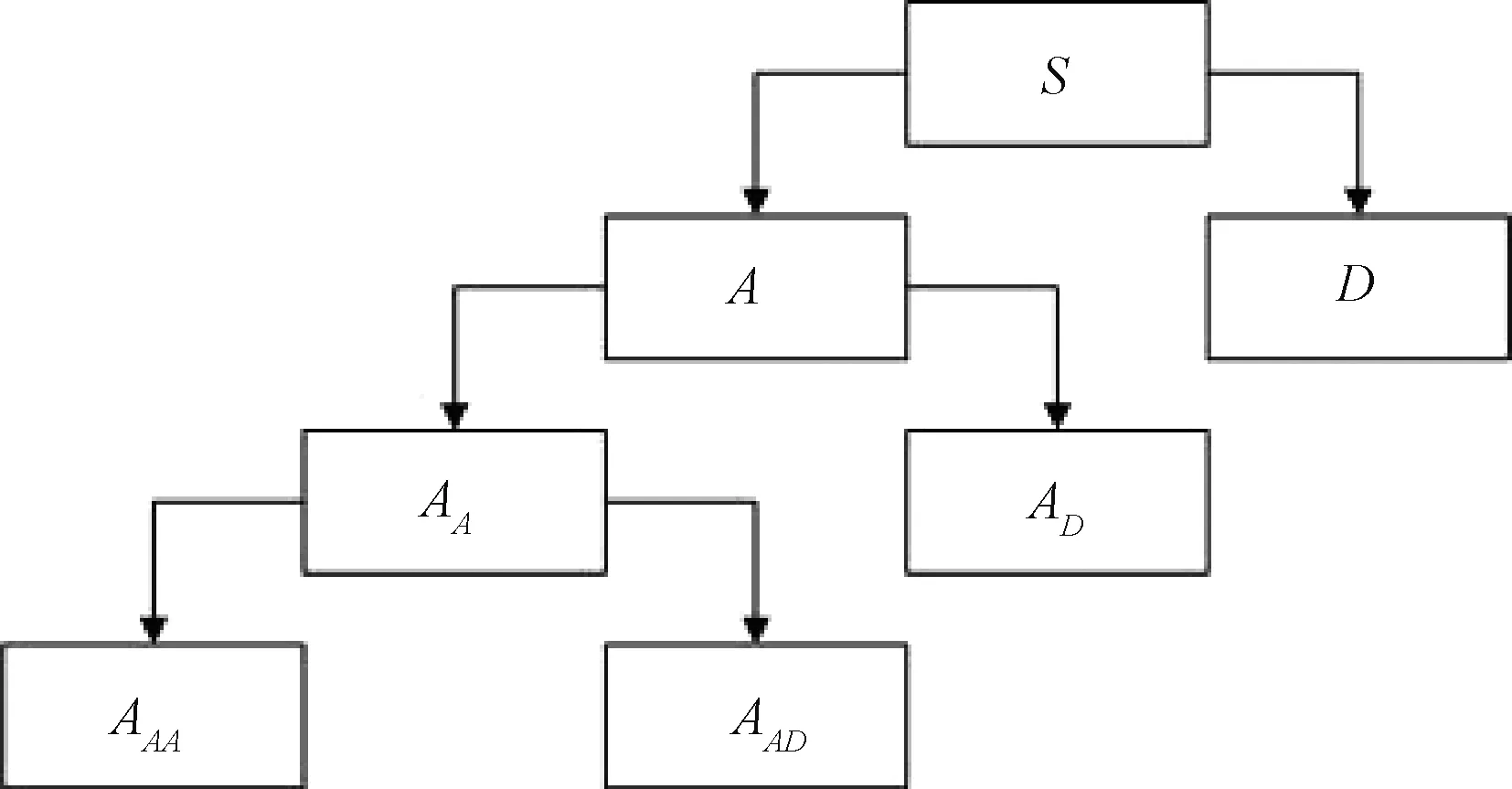
图2 离散小波分解示意图
假设原信号的频率范围为0~Fs,则离散小波变换分解系数D1包含信息的频率成分范围是Fs/2~Fs,系数D2包含信息的频率成分范围是Fs/4~Fs/2,系数D3包含信息的频率成分范围是Fs/8~Fs/4,系数A3包含信息的频率成分范围是0~Fs/8,依次类推。与离散小波变换相比,小波包变换对低频、高频成分都做了分解,分解更加精细,分解结构见图3。
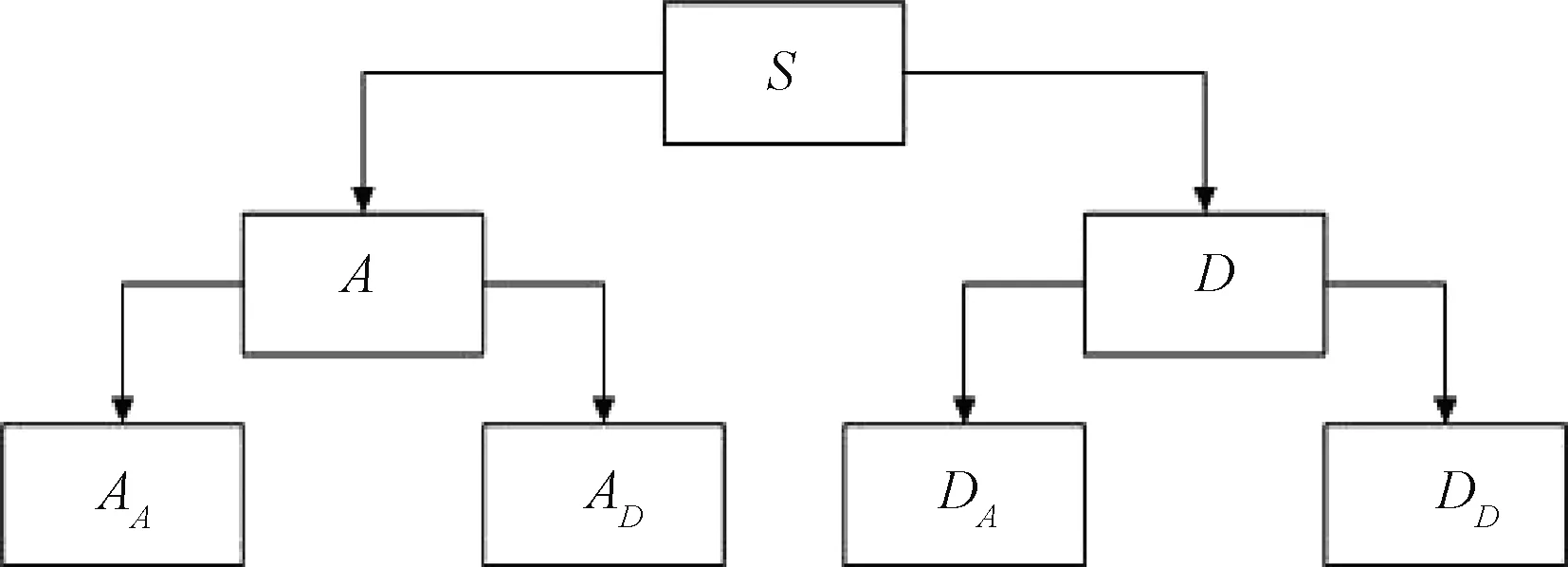
图3 小波包分解示意图
1.2.2 小波降噪阈值的分类
常用的阈值降噪方法有硬阈值法和软阈值法,两者都是对小波分解后的系数进行阈值操作,方法如下:
(1) 硬阈值函数
(3)
(2) 软阈值函数
(4)
阈值λ直接影响信号降噪的效果。λ过大,在滤掉噪声的同时也会把有用信息给滤除;λ过小,会保留噪声,达不到降噪效果。目前比较流行的阈值选取规则有以下几种:
(1) 固定阈值规则(sqtwolog规则)
(5)
式中:σ为噪声的标准方差;N为信号的长度。
这种方法的含义是:如果信号里存在N个相互独立且同分布规律的噪声,那么经过小波变换后它的系数最大值小于λ1的概率随N的增大而趋于1。
(2) Stein无偏似然估计阈值规则(rigrsure规则)
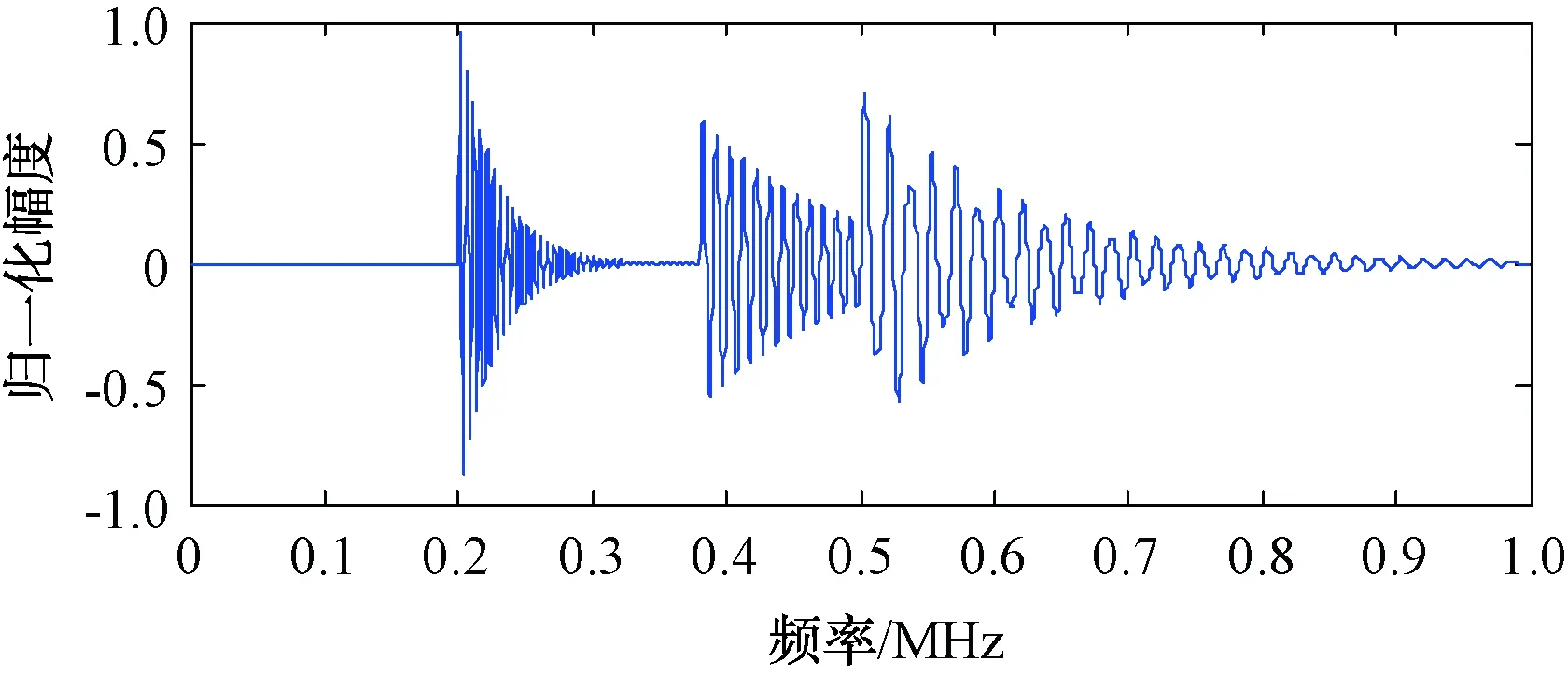
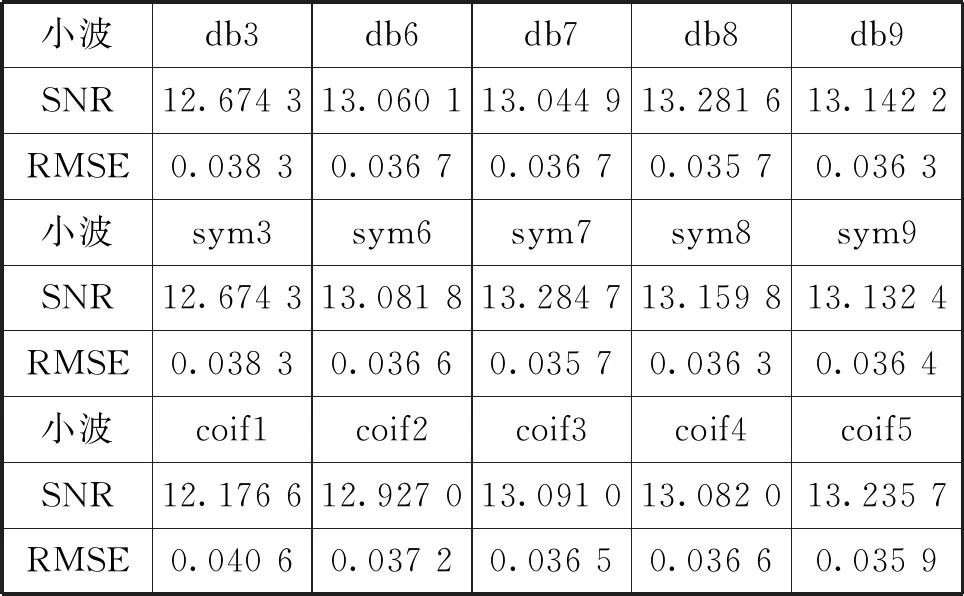
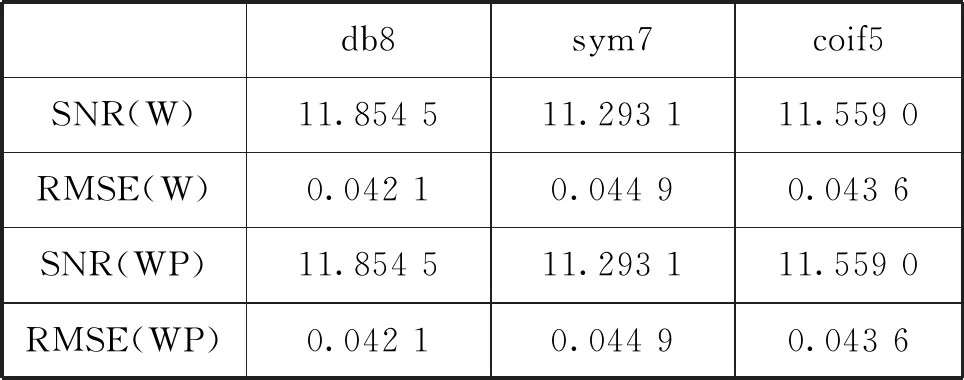
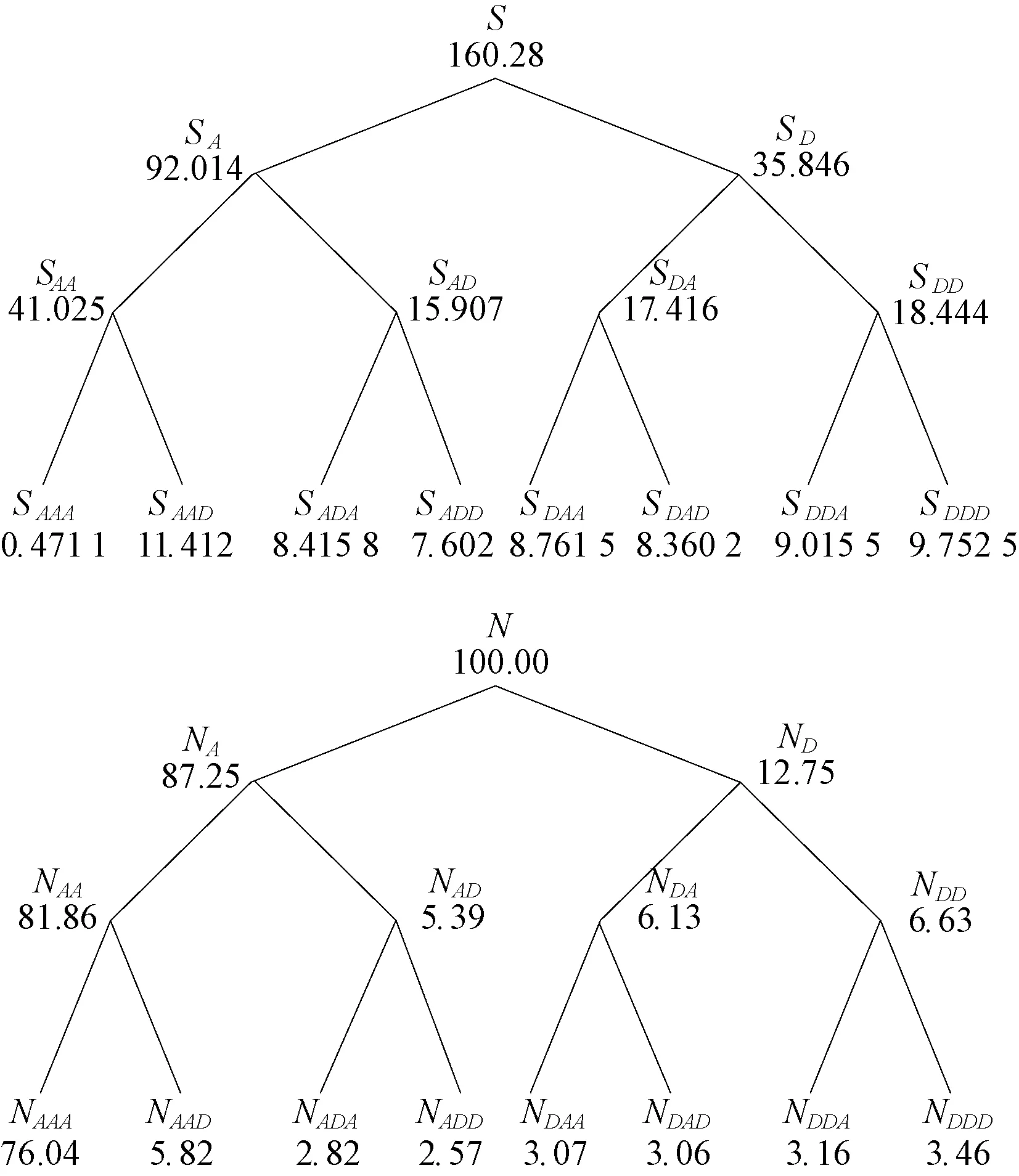
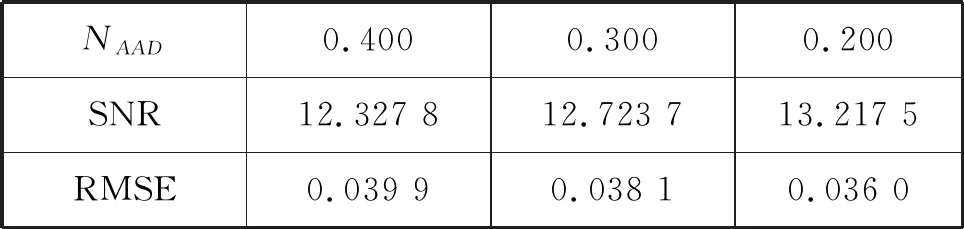
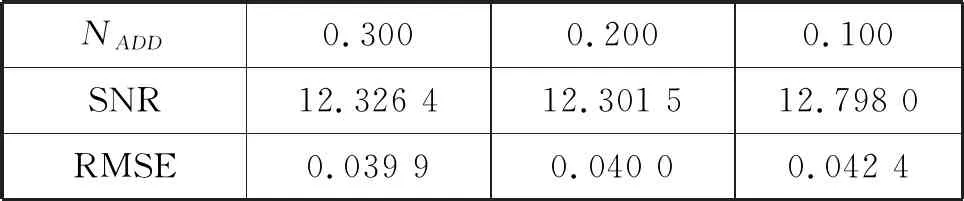
这种方法选取阈值的步骤是:设信号长度为N,取向量P=[p1,p2,…,pN],并且p1 (6) 用R中的最小rj作为风险值,由rj的下标量j得到对应的pj,则阈值λ2=σ(pj)1/2,σ是噪声的标准方差。 (3) 启发式阈值规则(heursure规则) 启发式阈值是前2种阈值的综合。核心是根据信噪比的状况选取阈值,若信噪比低,则使用固定阈值;若信噪比高(含噪声小),则使用Stein无偏似然估计阈值。设s为小波系数的平方和,m为小波系数的个数,令μ=(s-m)/m,η=(log2m)3/2/m1/2,则阈值为: (7) (4) 最大最小值阈值规则(minimaxi规则) 最大最小阈值是一种固定的阈值选择,这种阈值处理是有误差的,但它最小化了降噪信号和原始信号的极大均方差: (8) 声发射信号是一种典型的非平稳、非静态信号,其物理模型公式如下: s(t)=A(t)ejθ(t) (9) 根据公式(9)构造如图4所示的声发射信号。 图4 仿真信号 工程实际中的声发射信号会夹杂着噪声,噪声的类型一般包括机械噪声和电磁噪声。机械噪声的来源主要有:摩擦、撞击、流体运动等。电磁噪声的来源主要有:采集电路前置放大部分固有噪声、接地不当引入噪声、电子噪声(电源、继电器、无线电)等。加入噪声后的仿真信号如图5所示。 图5 加入噪声后的声发射信号 信号降噪过程中,选用不同的小波基函数和不同的阈值会有不同的降噪效果,这是信号降噪问题研究的关键。根据式(1)含噪信号模型,工程上评价降噪效果的标准有如下2个参数:信噪比(SNR)和均方根误差(RMSE): (10) (11) 信噪比越大,均方根误差越小代表信号所包含的信息量大,降噪的效果好。以下着重利用这2个参数研究声发射信号降噪过程中小波函数、阈值的选择问题,并比较小波降噪和小波包降噪的效果。 2.2.1 小波函数的选择 小波函数的种类很多,包括Haar,Daubechies,Symlets,Coiflets,Morlet,Mexican Hat,Meyer等。为进行离散小波变换和小波包变换,小波函数必须具备正交性,所以Morlet,Mexican Hat,Meyer等小波函数不适用于信号降噪。本文采用自适应阈值算法,对含有5 dB噪声的声发射信号分别用db3,db6,db8,db9,sym3,sym6,sym8,sym9,coif2,coif3,coif4,coif5小波函数降噪处理,处理结果见表1。 表1 不同小波基函数的降噪效果 由表1可见,db8,sym7,coif5等小波函数的降噪信噪比较大,而且均方根误差较小,说明这些小波函数与信号的相似度最好,可用于降噪。 2.2.2 阈值的选择 在上节的基础上,利用sym7小波,对常用的4种阈值选取规则在硬阈值法和软阈值法的基础上进行比较。比较结果见表2[4-5]。 由表2可见,对声发射信号的处理中,在软阈值降噪法基础上,用Stein无偏似然估计得到的阈值取得的降噪效果最好,但数据无法表明硬阈值法和软阈值法哪个效果更好。文献[6]对此现象做了研究,指出硬阈值法不能完全去除噪声,容易引起重构信号的局部振荡;软阈值法通过减少所有系数的阈值来减少噪声,重构信号虽然光滑但精度差。 2.2.3 小波降噪和小波包降噪的比较 由1.2.1节的论述可知小波包对信号在频域的分解比小波对信号在频域的分解更加精细,小波包变换对信号的高频成分也做了分解。本文对含有噪声5 dB的声发射信号在同一阈值的基础上,分别用小波变换和小波包变换降噪,效果见表3。 表3 小波降噪和小波包降噪的比较 由表3不能看出小波降噪和小波包降噪的差别。现选择sym7小波函数对信号分解,通过分析小波包分解的能量图可以看出:最底层的分解中,含有噪声的声发射信号的熵值在SAAA节点最小,说明能量主要集中在该节点上,经计算该点能量值为76.04,见图6。 图6 小波包分解节点的熵值(上)和能量(下) 小波降噪与小波包降噪区别不大,而声发射信号的能量主要集中在低频范围内,由于NAAD节点的能量为5.82,较其它尺度的节点包含能量大,可以通过调节该节点的阈值来找出降噪效果和节点能量的关系。设计阈值和降噪效果如表4所示。 表4 高能量点阈值与降噪的关系 再看看小能量的节点,通过图6可以发现节点NADD的能量为2.57,比较小,可以调节这两节点的阈值来验证降噪效果和节点能量的关系(保持NAAD节点的阈值0.4不变),设计阈值和降噪效果如表5。 表5 低能量点阈值与降噪的关系 比较表4和表5可以得到,声发射信号的降噪效果与分解层节点的能量有关,高能量点的阈值减少时或者低能量点的阈值增加时,降噪效果得到提高。 综合以上分析可以归纳出:(1)当声发射信号能量比较集中,利用小波变换就可以很好地降噪,并且能减少计算量;若能量比较分散,小波包降噪因为尺度比小波降噪更加精细,降噪效果要比小波变换好;(2)对能量分散的信号进行小波包变换后,针对不同频段能量的大小分别设置不同的阈值,可以获得更好的降噪效果。 图7对仿真声发射信号进行了局部放大,比较原始信号、小波降噪后的信号以及小波包能量改进降噪后的信号,可以发现依赖小波包能量改进降噪的效果要比小波降噪的效果好。 图7 原始信号、小波降噪信号、能量改进小波包降噪信号2 声发射信号的小波降噪
2.1 声发射信号的仿真
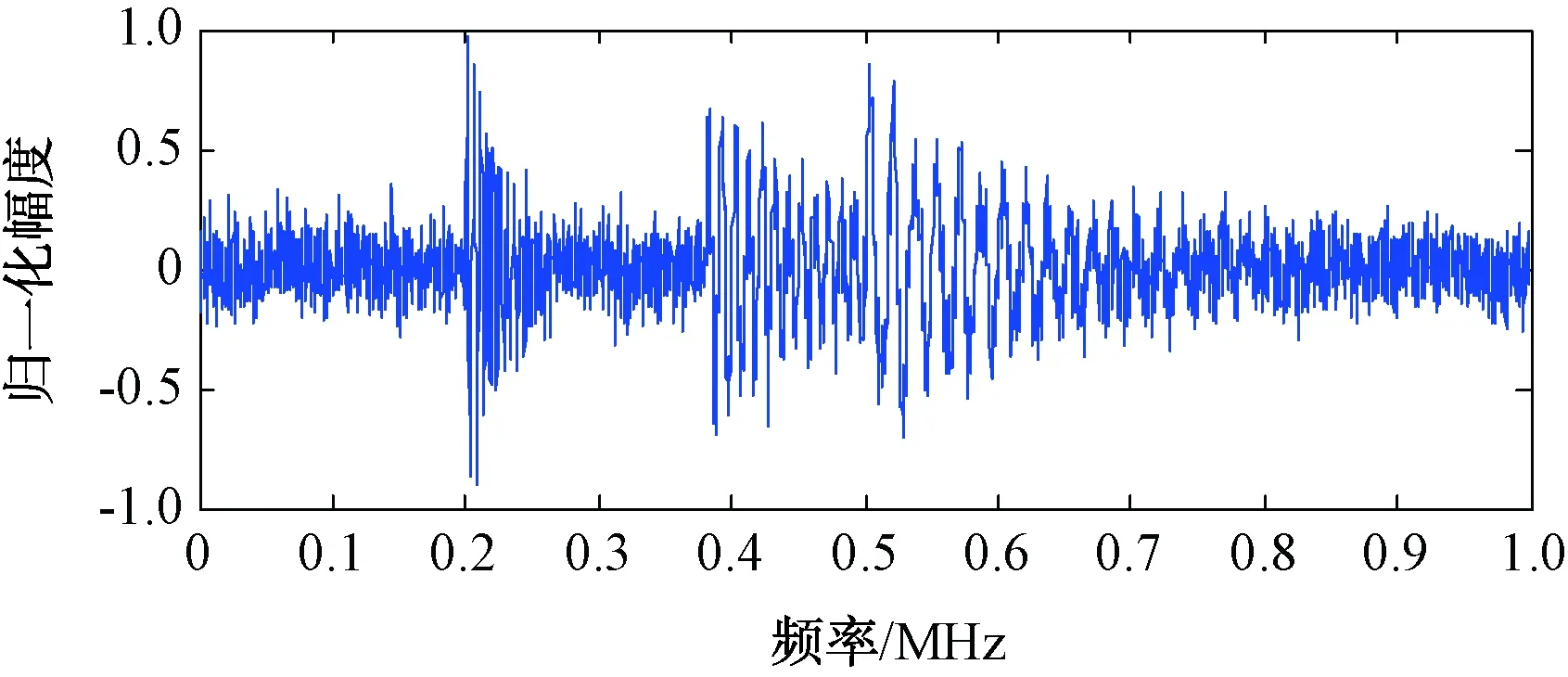
2.2 声发射信号的降噪
3 结束语