基于改进人工势场法的无人船动态路径规划算法研究

陈凯翔,周姝婧,许 强,闵柏成

(中国船舶集团有限公司第七二三研究所,江苏 扬州 225101)

0 引 言

无人船是一种可在复杂水域环境中,利用感知装置进行探测,并完成既定任务的小型水面运动平台。相较于传统船舶,无人船摆脱了对船员历史经验教训的依赖,综合了环境感知、信息融合、人工智能、规划决策和自动控制等技术,能够智能化完成特殊任务需求,使船舶更为经济、环保、安全和便捷。无人船航行路径规划是保障无人船自主、安全航行的关键技术之一,如何及时、有效地避碰更是其中的重点和难点[1]。

路径规划是综合考虑无人船机动性能及水面环境约束等因素而设计出的一条从起点快速抵达目标位置的最优路径[2]。目前比较常见的有栅格法、A*算法、蚁群算法、Voronoi图法、神经网络算法和人工势场法等。其中栅格法和A*算法是通过启发式信息估算下一步行进的最优节点位置,常用于全局路径规划,它一般需要大量的环境数据和先验知识作为支撑,计算繁杂,并行性差,实时性弱,与环境粒度的大小密切相关[3]。蚁群算法具有很好的算法收敛和并行分布式,可做到局部最优,但所规划出的路径却并不平滑,且随着地图范围的扩大,所需计算的工作量和时间也将急剧增加[4]。Voronoi图法容易构造实现,时效性较强,计算量较小,具有很好的环境兼容性,但特征元素较难选取,所规划出的路径不够平滑[5]。神经网络算法具有很好的分类准确度,可并行分布处理,具有较强的鲁棒性和容错能力,但它通常需要大量的样本环境数据进行学习,高昂的计算成本和更长的开发时间也很难令人满意[6]。人工势场法的数学机理简单,计算量小,硬件要求低,运算迅速,且满足实时控制需求,规划路径较为平滑,但它往往容易陷入局部极小值点而造成局部振荡和目标不可达现象,导致算法停滞[7-8]。

本文便是基于人工势场法(APF)的思想,引入了碰撞危险度、虚拟引力和偏航引力,提出了一种动态路径规划算法,使无人船在船舶动力学约束条件下能够快速跳出局部振荡和目标不可达的怪圈并抵达目标终点。仿真结果表明,该方法在不同环境下都可以规划出一条安全、可靠、平滑且经济的路径。

1 传统的人工势场法

众所周知,在磁场中,2个同性物体之间存在着排斥力,该力会阻止两者的靠近,被称为斥力;2个异性物体之间存在着吸引力,该力会不断促使两者相互靠近,被称为引力。而人工势场法便是借鉴了这一思想,将无人船所处的环境抽象成一个势力场,障碍物看成同性物体,目标终点看作异性物体,那么无人船在航线上所受到的作用力就可以认为是引力和斥力的合力叠加,其下一时刻的行驶方向便由合力方向所决定。

如图1所示,将无人船看做一个质点,在某一时刻其行驶空间可视为一个二维区域。假设此时无人船的位置为P(X,Y),目标终点的位置为G(XG,YG),第i个障碍物的位置为Oi(Xi,Yi),那么无人船所处的任意一点的势场环境就可以当成是由目标终点和障碍物所形成的合势场Ut(P),表示为:

Ut(P)=Ua(P)+Ur(P)

(1)

式中:Ua(P)表示引力势场;Ur(P)表示斥力势场。

无人船在P位置所受到的合力为:

F(P)=Fa(P)+Fr(P)

(2)

式中:Fa(P)和Fr(P)分别表示无人船所受到的引力与斥力作用,无人船在合力F(P)的作用下前进。

1.1 引力势场

当无人船处于目标终点作用的引力势场中时,所受到的引力方向是朝向目标终点的。根据引力势能的原理可知,目标终点对无人船的引力势能Ua(P)会随着两者间的距离减小而减弱,受到的引力作用Fa(P)也随之变小,反之则变大。在抵达目标终点时,引力也变为零。因此可由势能与距离的关系定义无人船所受到的引力势能为:

(3)

式中:ka为引力增益系数;dG为目标终点和无人船之间的相对距离。

Fa(P)=-▽Ua(P)=kadG

(4)

式中:dG为目标终点和无人船之间的相对距离,其值可根据两者相对位置关系获得:

(5)

1.2 斥力势场

在二维行驶区域内,为避免和无人船发生碰撞,障碍物会对无人船产生斥力影响,距离决定了该斥力的影响程度。当无人船进入到斥力势场影响区域内时,随着与障碍物之间的距离越来越短,所受到的斥力将会逐渐增加,反之减小。而当无人船离开斥力势场影响区域后,受到的斥力作用为零。由此可定义无人船所受到的第i个障碍物的斥力势能为:

(6)

式中:kr为斥力增益系数;doi表示第i个障碍物与无人船之间的相对距离;Di表示第i个障碍物的斥力势场影响半径,其通常由无人船最小安全制动距离Dmin来决定。

根据势能Ep和力F的关系,第i个障碍物的斥力表示为:

Fri(P)=-▽Uri(P)=

(7)

则无人船在斥力势场中受到的合力表示成:

(8)

1.3 局部极小值问题

采用人工势场法形成的路径,能够高效、准确、实时地规避障碍物,且路径平滑安全,应用优势十分明显。但同样地,它也有自身的缺陷之处,即局部极小值问题[9]。

由于无人船行驶位置发生变化时,其势场大小和行驶方向也会随之变化,因此,如图2所示,在某些位置上时,无人船受到的引力Fa(P)和斥力Fr(P)相等或近似的时候,F(P)≈0,无人船到达零势能点。在零势能点上,无人船将会停止不动或在该位置附近来回徘徊,形成局部振荡或者目标不可达现象,从而导致算法停滞,无法继续向目标终点前进。

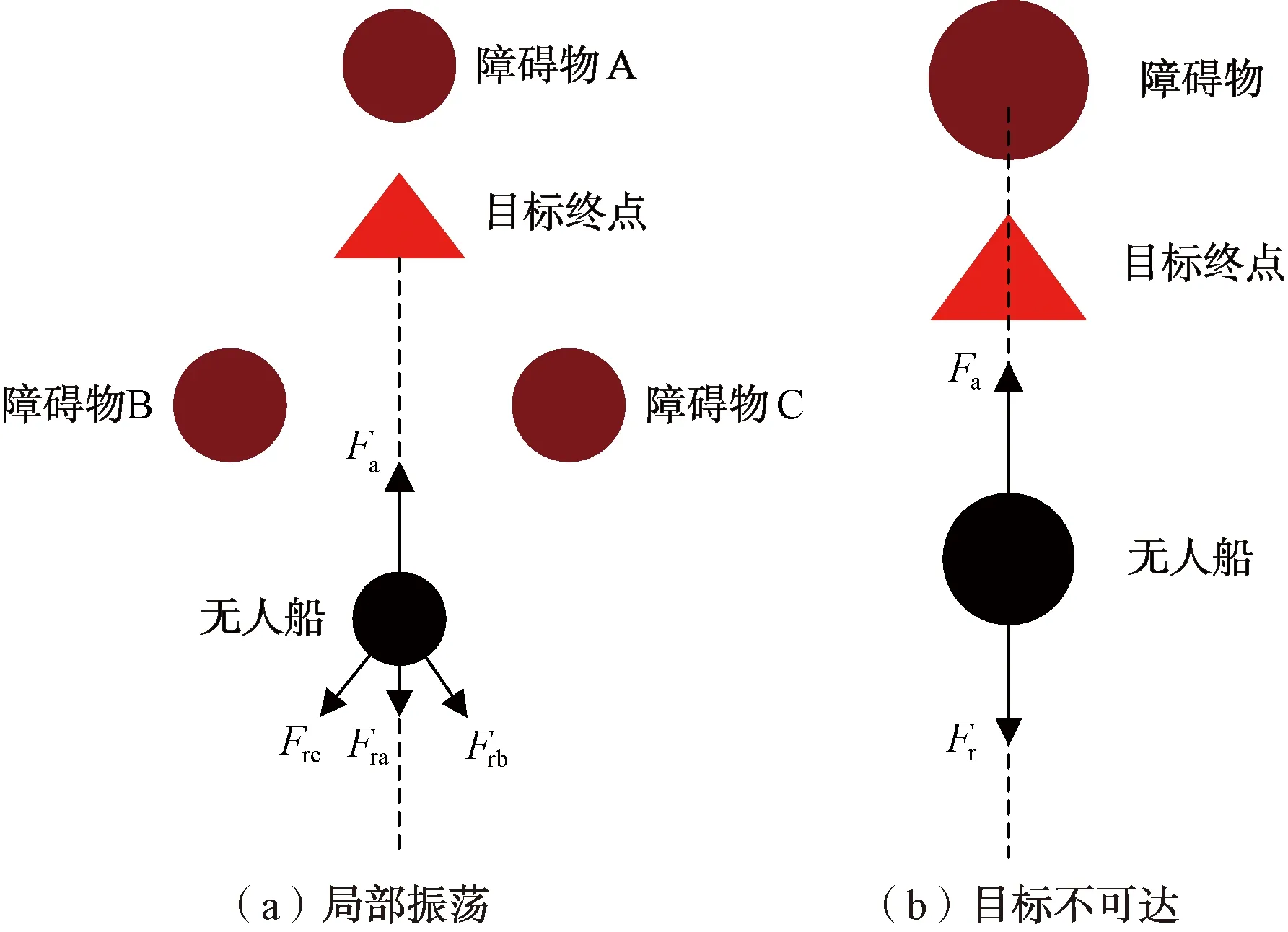
图2 局部极小值点受力情况

2 基于改进人工势场法的动态路径规划算法

动态路径规划的目的是引导无人船快速有效地避开障碍物,从而寻求一条经济适用的航行路线。在实际航行过程中,需要从碰撞危险程度和船舶动力学约束的角度加以分析,从而对传统的人工势场法加以改进,使其快速形成一条安全、平滑、机动耗能少的动态路径。

2.1 障碍物的危险度判定

在无人船实际航行过程中,遇到的所有障碍物是否需要规避,可根据碰撞危险度指标来对环境感知设备传送的障碍物信息进行评估。根据衡量指标的不同,碰撞危险度可分为空间碰撞危险度(ISCR)和时间碰撞危险度(ITCR)[10]。其中,ISCP描述了无人船和障碍物在保持当前运动状态的情况下空间上发生碰撞的可能性;ITCP描述了在发生空间碰撞的前提下,从当前时刻到形成空间碰撞危险的紧迫程度。因此,可定义碰撞复杂度表达式为:

(9)

(10)

ICR=ISCR·ITCR

(11)

式中:(x,y)t表示在t时刻障碍物的位置坐标;Dt表示无人船与障碍物之间的安全航行阀值,通常由无人船在平面投影上的最长边来确定;Tmin由最小安全制动距离Dmin与无人船当前航速V所确定;TCPA表示最小会遇时间,由无人船和障碍物之间的相对距离与相对速度计算所得;TG表示无人船按当前航速行驶到目标终点所需的时间。

因此,为了区分障碍物对无人船的影响程度,可在原有的斥力函数中引入碰撞危险度因子:

(12)

2.2 改进人工势场法模型

在传统的人工势场法中,由于势场系数的影响,在局部位置上达到受力平衡,会导致局部极小值现象的产生。如果仅仅是通过调整引力增益系数或斥力增益系数来调节,也只是将局部极小值点偏移得离目标终点近一些或远一些,并不能从根本上打破这种受力平衡。因此,本文提出虚拟引力Fv(P)作为一个新的外力打破这种受力平衡,促使无人船偏航,从而引导无人船尽快驶离障碍物区域。

如图3所示,虚拟引力Fv(P)的受力方向与斥力Fr(P)方向保持垂直,且偏向于引力Fa(P)的一侧,即满足以下条件:

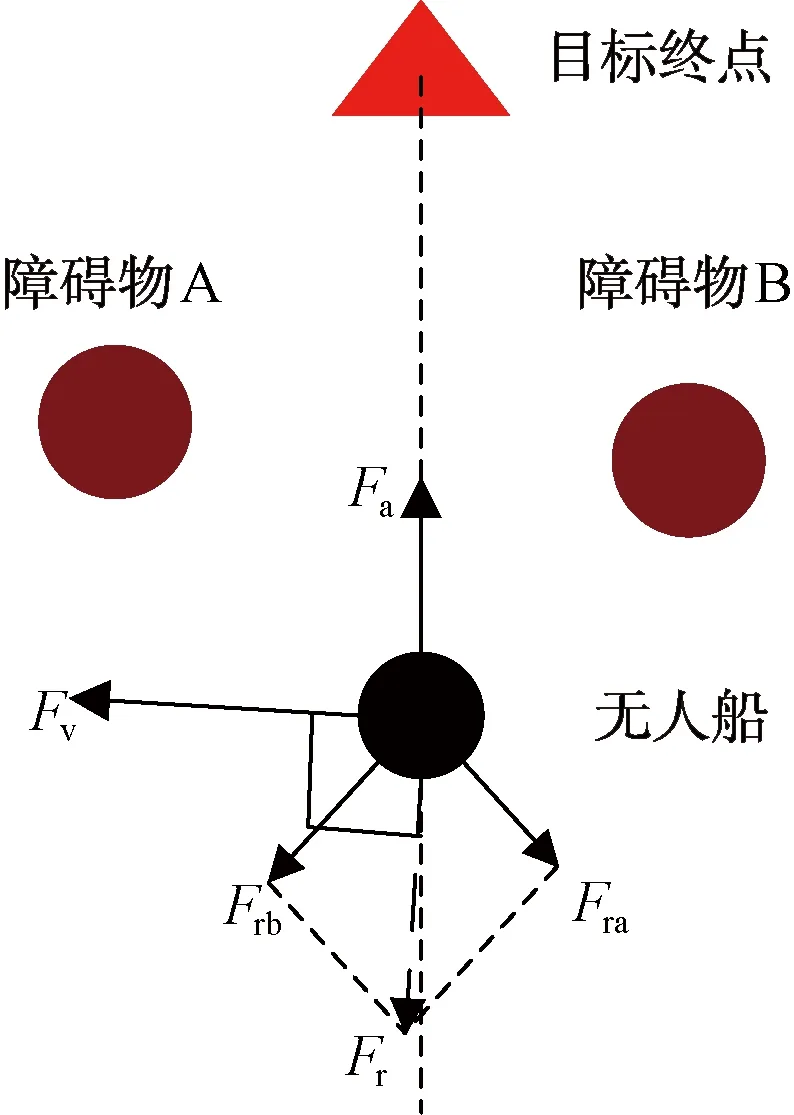
图3 虚拟引力的引入

(13)

式中:f表示虚拟引力增益系数,为使无人船能尽快转向,f应当尽可能使Fv(P)>Fr(P),因此可表示为:

(14)

这样可以保证,在障碍物斥力影响区域范围外,即Fv(P)=Fr(P)=0时,仅引力Fa(P)发生作用,促使无人船快速向目标终点靠近;而在障碍物斥力影响区域范围内,由于存在Fv(P)与Fr(P)垂直,推动无人船远离障碍目标。但当无人船避让完障碍物后,此时的Fv(P)和Fr(P)再次变为0,仅引力发生作用,此时无人船会直接向目标终点行进。无人船此时的行进路线为一条全新的航线,而不是原计划航线(在不考虑障碍物影响情况下原先规划的航线)。因此,需要在原有的引力函数中增加原计划航线对无人船的吸引和约束,使得无人船偏离原计划航线后仍然能不断地向其靠拢。

如图4所示,当无人船与原计划航线间的垂直距离超过偏航距离阀值Dp时,无人船开始受到偏航引力Fp的约束,促使无人船向原计划航线靠拢;而未超过偏航距离阀值Dp时,偏航引力Fp未产生作用,无人船依旧在Fa(P)、Fv(P)和Fr(P)的联合作用力下,远离障碍物。由此形成改进后的引力函数为:

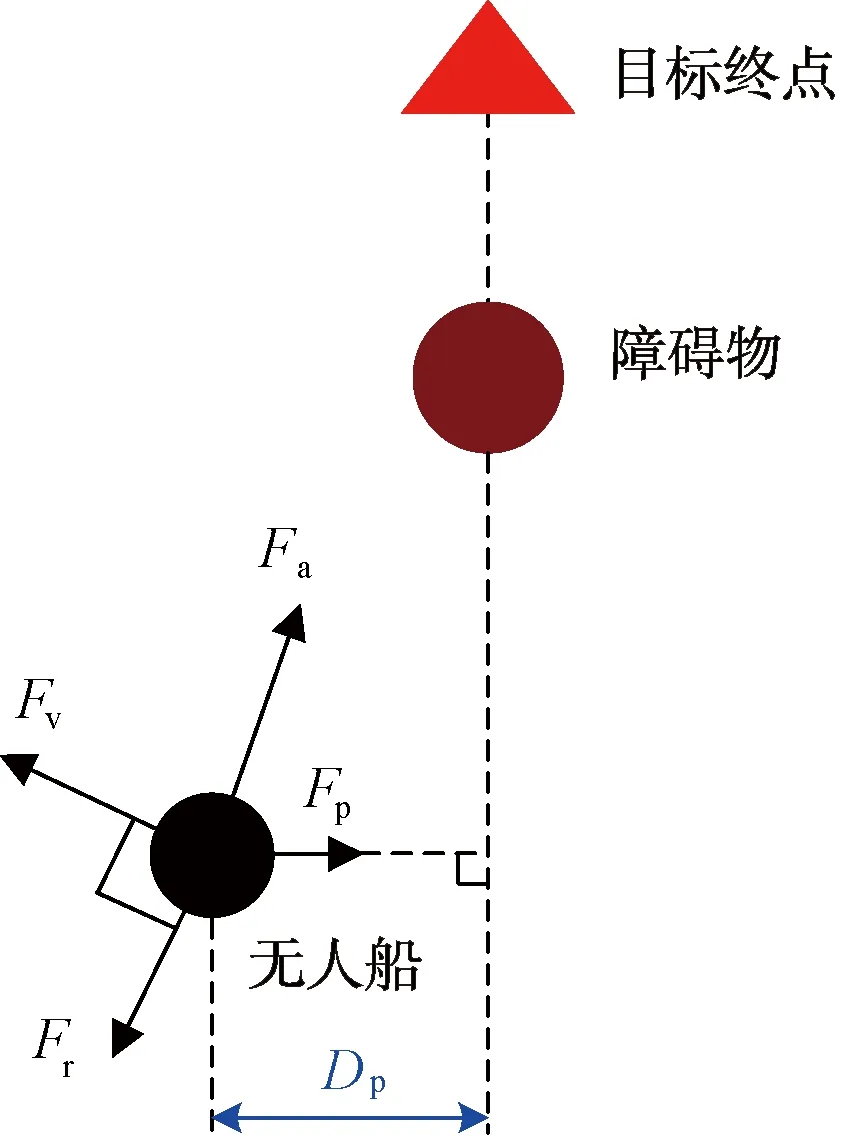
图4 改进后的受力示意图

(15)

式中:kp表示偏航引力增益系数;DL表示无人船到原计划航线的垂直距离。

因此无人船所受到的联合作用力为:

F(P)=Fa(P)+Fr(P)+Fv(P)+Fp(P)

(16)

2.3 动态路径规划算法

为了使规划出的动态避障路径更符合无人船的操纵特性,需要考虑船舶动力学的约束,即无人船在进行转向时是一条光滑的弧线或曲线,而不是尖锐的拐角,因此需要通过无人船最大偏转角度差Δθmax对动态路径规划算法进行约束和限制[11-12]。根据弧度公式Δl=Rmin·Δθmax和距离公式Δs=V·Δt可知,当Rmin=Dt=50 m,V=10 m/s时,无人船在1个转舵周期(设定为0.2 s)内的最大偏转角度差Δθmax为0.04°,即连续2个偏转角度之间的变化率不应该超过0.04°。

由此结合传统的比例、积分、微分(PID)+MMG船舶运动控制模型对无人船进行控制,可设计形成的基于改进人工势场法的无人船动态路径规划算法如下:

(1) 根据环境感知设备(即探测雷达、激光跟踪监视设备或超声探测设备等)实时传送的环境信息,判断有无障碍物。若存在障碍物,则执行步骤(2);否则执行步骤(6)。

(2) 由式(9)、(10)与(11),计算出无人船周边最小安全制动区域Dmin范围内的所有障碍物的碰撞危险度ICR。

(3) 根据无人船当前的航向θ、航速V以及与障碍物之间的相对距离L、无人船安全航行阀值Dt,判断是否需要紧急停船。如需要紧急停船,则关闭无人船发动机;否则执行步骤(5)。

(4) 通过式(8)与(12),得到所有障碍物对无人船的总斥力之和Fr(P)。

(5) 通过式(13)与(14),获得虚拟引力Fv(P)。

(6) 根据式(15),计算无人船受到的目标引力Fa(P)。

(7) 根据无人船当前的位置信息,对船只的偏航程度进行判断,并求得偏航引力Fp(P)。

(8) 通过式(16),确定无人船在势场中所受合力方向。

(9) 根据无人船当前的航速V,判断是否需要重新启航。如需要重新启航,则开启无人船发动机,并执行步骤(10);否则直接执行步骤(10)。

(10) 由当前航速与限定航速间的差值,进行速度管理,调整航速V。

(11) 根据无人船当前的航向θ和舵角φ、合力F(P)的方向、最大偏转角度差Δθmax与PID船舶控制模型,给出无人船的操舵舵角。

(12) 根据舵角和MMG船舶运动模型,保持无人船继续航行。

算法流程图如图5所示。

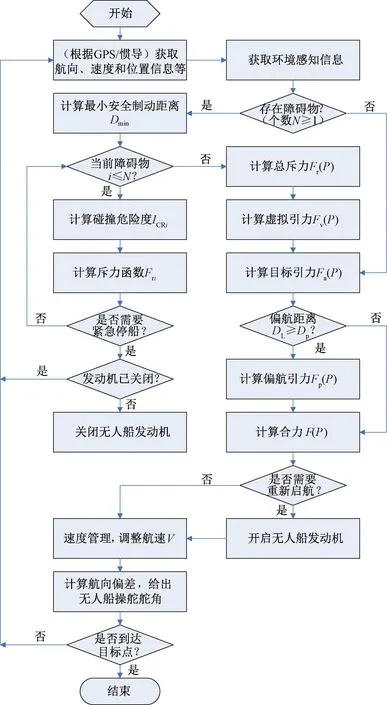
图5 无人船动态路径规划算法

3 仿真实验结果与分析

为了验证改进后的动态路径规划算法的有效性,本文采用MFC对算法进行了仿真,通过模拟多个目标的复杂环境,求解出一条经济有效的可行路径。

如图6(a)所示,设定无人船的起点为(0,0),目标终点为(0,2 000 m),航行速度为10 m/s,生成理论航迹如图中虚线所示。通过障碍圆模拟在航行过程中遭遇的障碍目标,分别设置圆心为A(-50 m,1 000 m)、B(50 m,500 m)和C(0,900 m),障碍圆的半径为40 m,其中C为动目标,运动速度为5 m/s,航向为180°。安全航行阀值Dt=50 m,安全制动区域范围Dmin=300 m,偏航距离阀值Dp=50 m,最大偏转角度差Δθmax=0.04°,实际航行轨迹如图6实线所示。

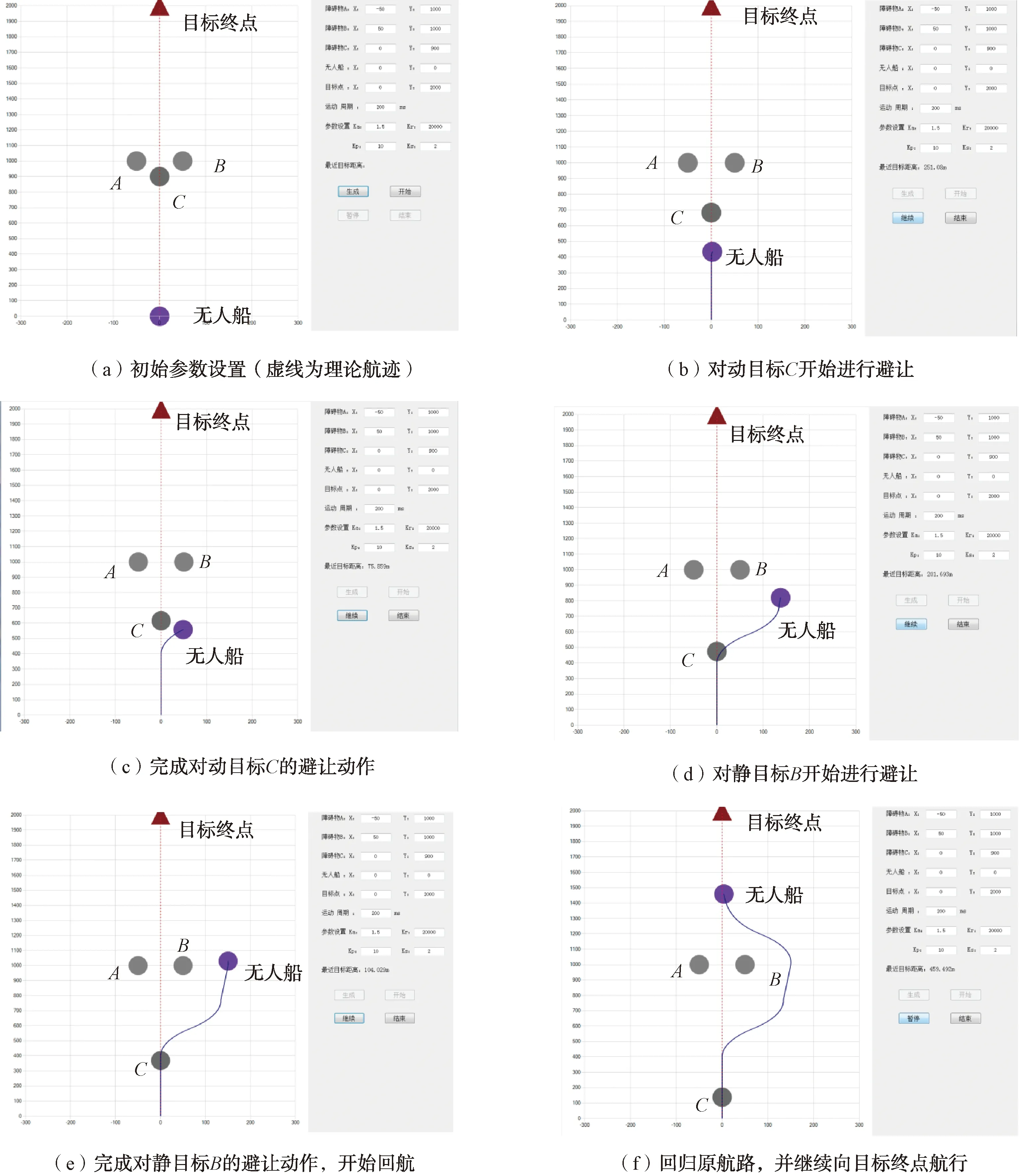
图6 算法仿真效果图

在航行过程中,障碍目标在无人船最小安全制动区域范围Dmin之外时,船只保持原航速和航向航行。当遇到障碍目标C,对其进行碰撞危险度判断,并执行避让动作(向右偏航),如图6(b)和6(c)所示。动目标C避让完成后,此时在无人船视距范围内仅有障碍目标A和B存在,判断B可能存在碰撞危险,因此继续对目标B执行避让动作(向右偏航,此时偏航代价最小),如图6(d)和6(e)所示。所有障碍目标均避让完成后,无人船在偏航引力和目标引力的作用下,向原计划航线逐渐靠拢,直至回归原航线,如图6(f)所示。

4 结束语

本文对人工势场法的原理与不足进行了分析,并通过引入虚拟引力、偏航引力和碰撞危险度等方法,对引力函数和斥力函数进行了改进,可以解决局部极小值问题,使动态路径规划算法能够在复杂障碍环境中求得最优解。MFC仿真结果表明,改进后的动态路径规划算法能够有效规避在航行过程中遇到的障碍目标,到达目标终点。本文采用理想化航行区域,而在实际工程应用中应当考虑狭窄水域这一特殊限制条件,因此可将狭窄水域的两岸抽象成静态障碍物,在实际的动态路径规划算法中进行考虑,增强其自主化和安全性。