基于ETKF 的协方差膨胀比较研究

陈 丽

（中国民用航空飞行学院理学院，四川 广汉 618307）

集合变换卡尔曼滤波[1]将集合成员视为可用于估计未知的状态向量和误差协方差矩阵的样本，以此避免对模型进行线性化处理。但有限的集合数目使得抽样误差协方差矩阵在长距离上产生伪相关问题，强烈影响滤波算法的性能。因此，已有研究引入了多种方法来规范误差的分析：如协方差膨胀（CI）[2]。

目前，协方差膨胀有两种方式：乘法膨胀和加法膨胀。乘法膨胀的原理是调整（通常增加）集合扩散，从而调整协方差，消除算法伪相关性。而加法膨胀可以处理由于模型误差的存在产生的误差低估问题，且对于模型误差是EnKF 方案外部的误差情况也可解决。但是目前越来越多的学者在相关研究中更多地考虑的是乘法膨胀法，对于加法膨胀的关注却较少。

因此，本文结合Lorenz3[3]和Lorenz96[4]模型以及ETKF 同化方案综合研究两种膨胀方式对同化效果的影响。

1 研究方法

1.1 集合变换卡尔曼滤波算法简介

在EnKF 框架中[5]，从集合开始分析

其中xa i表示在分析步骤的集合中的第i个状态向量，表示在预测步骤的集合中的第i个状态向量。

由于EnKF 中预报误差协方差矩阵Pf=Xf(Xf)T的秩至多为m-1，因此不可逆。但作为对称矩阵，它在其列空间S上是一对一的，这也是Xf的列空间，最小化可以在这个子空间S 中进行。将Xf视为从k 维空间Ω至S的线性变换，并在Ω中执行分析。在下面的讨论中，定义集合空间如下：

对于分析估计，利用卡尔曼增益的形式得到均值的最优系数向量wa：

其中δ=y-H()。

定义T=（，可以构建后验集合为

1.2 乘法膨胀法

乘法膨胀简单地将集合误差协方差Pf膨胀一个因子λ，以近似真实误差协方差Pf：

乘法膨胀的引入弥补了原始Pf中不包括的模型误差。

1.3 加法膨胀法

加法膨胀通过向每个集合成员中添加具有一定协方差结构的随机扰动来参数化模型误差。其表现形式如下：即给集合成员增加扰动←+εi并且=Q。

2 数值实验

本节将基于ETKF、ETKF混合乘法膨胀法（ETKF+MI）、ETKF 混合加法膨胀法（ETKF+AI）以及ETKF 混合乘法和加法膨胀（ETKF+MI+AI）在Lorenz3 与Lorenz96 模型上进行实验。所有实验的基本设置与文献[6]相同。实验性能的好坏用以下均方根误差（RMSE）进行衡量，其计算公式如下：

其中，x和x真分别为估计得到的模型状态和真实的模型状态。

2.1 Lorenz3 模型的实验

在本小节中，基于Lorenz3 模型进行实验，其模型方程表示如下：

其中，σ=10、ρ=28 和β=8/3。

我们做了4 个实验，考察观测误差R和集合数目m发生变化时算法的性能如何改变。每个实验都运行1000 次，舍弃前100 次结果，计算剩余900 次的平均结果见表1。

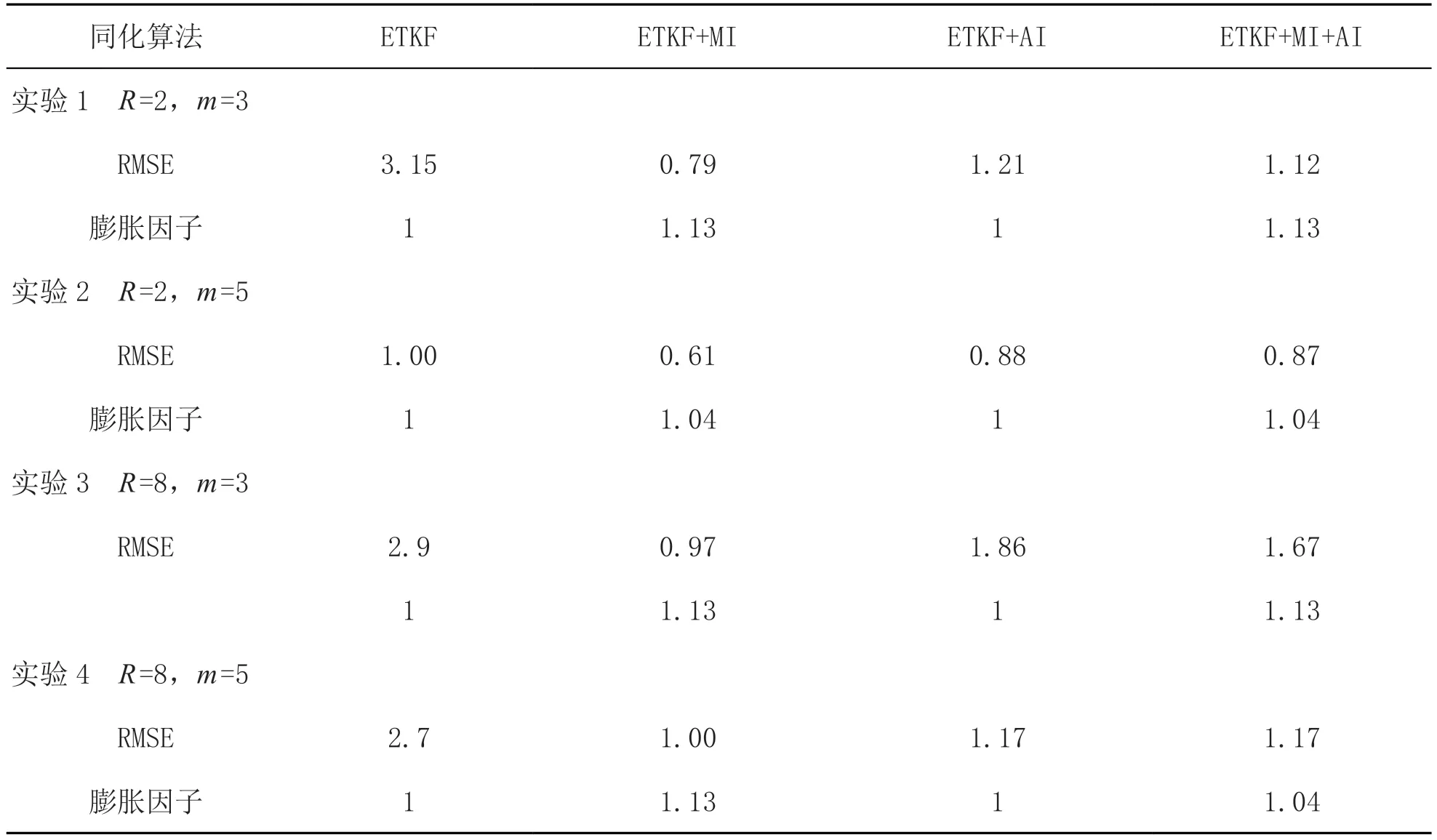
表1 Lorenz3 模型

从表1 中可知，在Lorenz3 模型中，观测误差较小，集合数目也较小时，不管引入乘法膨胀还是加法膨胀，算法性能都有较大提升，显然，仅添加乘法膨胀的算法性能最优，而两种膨胀方式叠加并没有显著提高算法性能，仅略微优于只混合加法膨胀的算法。当观测误差增大时，ETKF+MI 的RMSE 仍然是最低的，ETKF+MI+AI 次之，ETKF+AI 最高，增加集合数目后，仅添加加法膨胀的算法性能与两种膨胀方式结合的相同，这说明叠加引入乘法膨胀也无法提升ETKF+AI 算法的性能。

2.2 Lorenz96 模型的实验

Lorenz96 模型表达式为：

在Lorenz96 模型中，依然进行了4 个实验，考察观测误差R和集合数目m发生变化时算法的性能如何改变。每个实验运行1000 次，舍弃前100 次结果，计算剩余900 次的平均结果见表2。

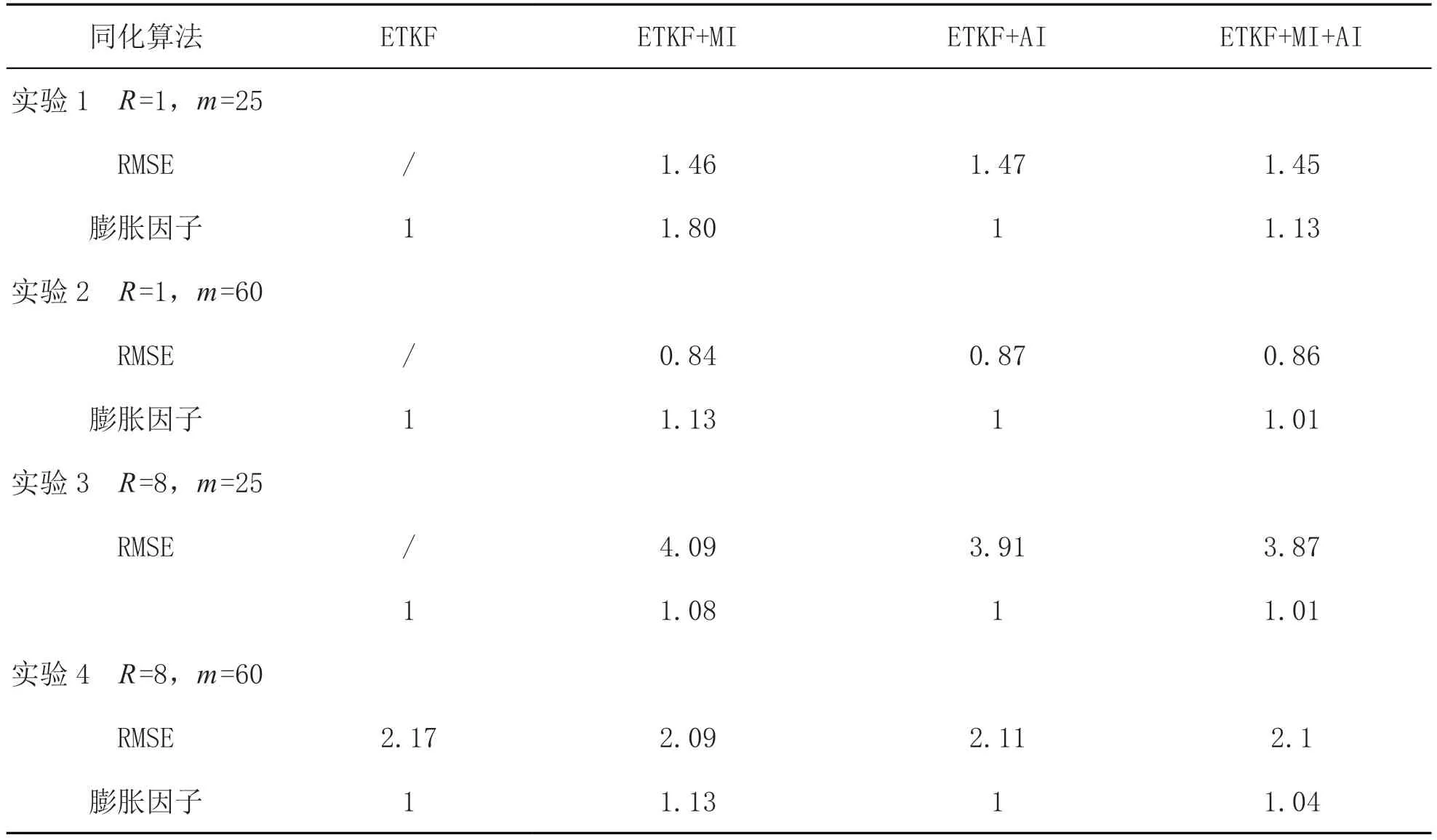
表2 Lorenz96 模型

如表2 所示，在Lorenz96 模型中，观测误差较小，集合数目也较小时（低于状态变量的数目）两种膨胀方式的融合算法性能最优，优于乘法膨胀，而加法膨胀性能较低，增加集合数目高于状态变量个数后，ETKF+MI的算法性能变成最优的，而ETKF+MI+AI 次之。当观测误差增大时，在集合数目较低时，ETKF+MI+AI 算法性能仍然是最优的，而将集合数目增加后，其算法性能又变成次优的。由此说明，与Lorenz3 模型不同，在非线性性更强的Lorenz96 模型中，两者混合的膨胀算法ETKF+MI+AI 可以在较低集合数目下显著提升同化算法的性能。

3 结论

协方差膨胀的引入可以显著提高算法性能，防止滤波发散。膨胀方式的选择则需要依托模型特点。在弱非线性模型中，无论观测误差是大还是小，集合数目是多还是少，在同化算法中仅考虑加法膨胀的算法性能是最优的，两者结合的算法次之，加法膨胀性能最低。在强非线性模型中，当集合数目较多时，不论观测误差的高低，乘法膨胀性能仍是最优的，这与弱非线性模型结果相同。但当集合数目较少，观测误差较低时，两者结合的算法性能变为最优，乘法膨胀次之，加法膨胀最低，随着观测误差增大，两者结合的算法性能依然是最优的，但乘法膨胀性能变为最低。由此说明，协方差膨胀方式的选择并不是固定的，需要根据模型非线性的强弱，观测误差的大小，以及集合数目进行综合考虑。