探索规律：感受字母表示数的优越性

文／赵维坤

同学们，代数发展的历史经历了三个主要阶段：公元3 世纪之前，人们主要用文字描述来表示数；接着，古希腊数学家丢番图首次引进缩写字母来代表未知的量，这个阶段可以称为半符号化阶段；数学真正进入符号代数阶段，始于“代数学之父”法国数学家韦达的创新，他系统地使用字母表示已知量、未知量，让字母可以像数一样进行运算，这才是代数的真正开始。

下面，我们通过动手操作、观察、猜想、推理、归纳等活动，在形象感知的基础上，找出规律、列出代数式，感受字母表示数的优越性。

画对角线

连接多边形不相邻两个顶点的线段叫做多边形的对角线。如图1 所示的四边形，我们可以画出2条对角线。

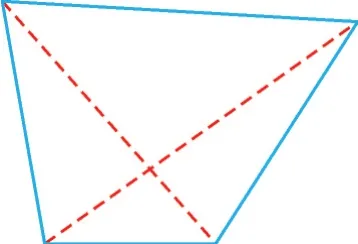
图1

同学们可以尝试画出五边形、六边形，并分别画出五边形、六边形的所有的对角线。

猜想七边形对角线的条数，然后画出七边形，并画出它所有的对角线，验证你的猜想。

随着多边形边数的增加，其对角线的条数也在变化。请同学们尝试写出多边形的边数n与其对角线的条数m之间的关系。

摆放棋子

如图2，请同学们按照前4 个图形中棋子的摆放规律，依次在后两个图形上摆放棋子。

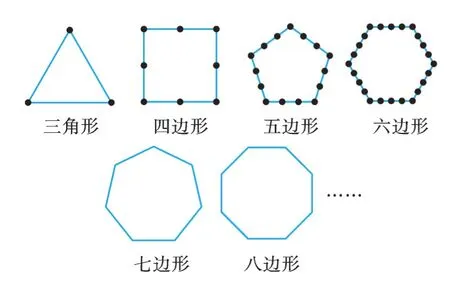
图2

照此摆法，九边形图形中棋子总数是多少？我们可以通过画出九边形来验证自己的猜想。那么，n边形呢？

画出图形

如图3，每个图形都是由边长为1 的单位长度的小正方形按照某种规律排列组成的。

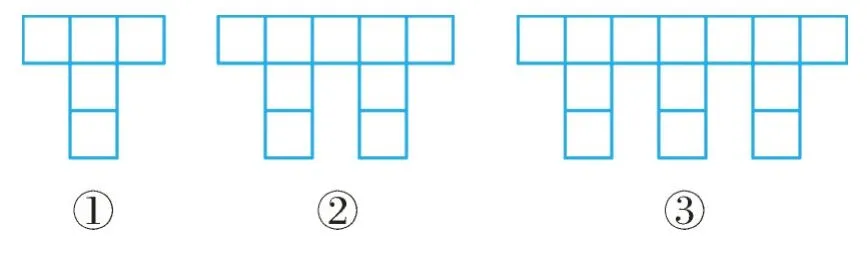
图3

请同学们手脑并用，做如下操作：

（1）按上述画图方式画出第4个图形；

（2）猜想：第5 个图形中小正方形的个数；

（3）思考：第n个图形由多少个小正方形组成？

同学们，用字母表示数量关系更具有一般性，能给我们解决问题带来便利。正如著名天文学家、物理学家开普勒所说，“数学是研究千变万化中不变的关系”，希望同学们带着数学的眼光继续打开“代数”知识的大门。