Bacterial turbulence in gradient confinement

Ningzhe Yan(颜宁哲), Chenliang Xie(谢晨亮), Hao Luo(罗昊), Yanan Liu(刘亚楠), and Guangyin Jing(经光银)

School of Physics,Northwest University,Xi’an 710127,China

Keywords: collective motion,bacterial turbulence,bacterial drop,gradient confinement

1.Introduction

Microorganisms can stir the surrounding medium to form disturbance flows by beating their flagella or cilium for locomotion.When these microswimmers move collectively at high density,the disturbed flows exhibit spatiotemporal chaotic vortices at a length scale much larger than the size of individual unit.[1]The spontaneous flow generated by tiny swimmers is fascinating and can be analogous to the inertial turbulence occurring at a large scale with high velocity,i.e.,high Reynolds number.[2–5]Bacterial suspension,for example,is recognized as a typical system far from equilibrium,in which the energy is continuously injected at the unit level and collective motion of coordinated individuals occurs.[3,6–9]This living turbulence plays a significant role in mixing enhancement and efficient molecular transport at low Reynolds number, and also facilitates the intracellular communications of the cells in biological systems.[10–16]From the fundamental point of view,the statistical features and laws are extremely interesting for the active flows in the systems with living microorganisms at vanishing Reynolds number.[1,17–20]

The individual bacterium injects the energy into the surrounding fluidic medium in a disordered way, which can be however collected to form ordered moving vortices.[21]Extensive studies have been conducted to understand this phase transition from the statistical point of view.[22,23]This new class of the spontaneous flow also raises questions on whether and how this living turbulence manifests the features and universality reminiscent of energy cascades in inertial turbulence.[3–5,24,25]The isotropic hypothesis, commonly applied to well-developed inertial turbulence, is both reasonable and necessary.However, microorganisms experience heterogeneous nutrient and oxygen supplies,compelling them to dynamically adapt to their environment and inject energy in an anisotropic manner.This raises the question of whether the isotropic assumption remains valid for bacterial turbulence across all scales.Moreover, the theoretical analysis and numerical methods for three-dimensional living turbulence are difficult to be realized by direct imaging under microscope.[26–30]Instead, two-dimensional living turbulence is feasibly observed within homogeneous films or channels.[3,7,24,31–33]Dombrowskiet al.introduced the dense bacteria into a sessile drop and Hele–Shaw confinement, and reported an interesting collective behavior due to oxygen diffusion dynamics.[6]It is however unclear how or to what extent,the properties and mechanisms of non-uniform living turbulence in bacterial suspensions differ from those of uniform counterparts.

Here,we trap dense bacteria inside sessile drops.This geometry,as a natural habitat for bacteria,generates an inevitable thickness gradient in the vicinity of the contact line.Since the characteristic size of the collective motion of the bacterial population depends on the smallest dimension of the confinement(i.e.,thickness),we,therefore,build a non-uniform living turbulence confined in the wedge at the corner of the sessile bacterial drop.Particularly,the air–liquid interface allows the diffusion of oxygen and provides a concentration variation along the radial direction of the drop due to the thickness gradient.This coupling of the thickness gradient and oxygen gradient allows a new type of heterogeneous turbulent flow in living bacterial suspension.The high activity of the motile bacteria contributes to the strong fluctuation of the living flows close to the contact line where oxygen is rich.However,the fluctuation increasingly decays due to less oxygen supply when the liquid layer gets thicker toward the drop center.Moreover, it turns out that this living turbulence is locally anisotropic at a unit scale while tends to isotropic at a scale around collective motion.The kinetic energy spectrum here exhibits geometric dependence at large wavenumber region, while a robust scalingE(k)∼k1with short wavenumber.This heterogenous turbulence built herein by controlling the activity of self-propelled units,suggests the possible spatial guide for the energy transfer across vortices in living turbulence.

2.Results and discussion

2.1.Non-uniform living turbulence

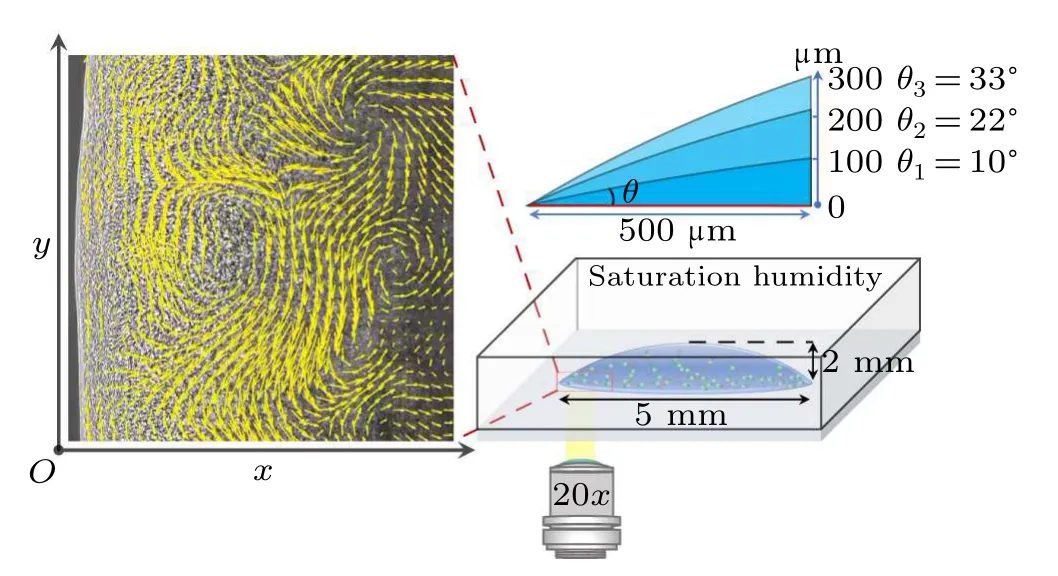
In our experiments,a specific region near the contact line of a sessile droplet is opted to study the collective behavior of the dense bacteria.Naturally,there is a wedge-shaped confinement between the substrate and the air–liquid interface with a gradually varying height from a few to hundreds of micrometers.A drop of bacterial suspension is transferred onto a horizontal glass slide and is kept within a closed chamber with saturated humidity to avoid the influences of evaporation and external disturbances.According to the wetting hysteresis behavior, drops with three contact anglesθ1= 10◦,θ2= 22◦andθ3=33◦are stably controlled through the subtle experimental setup as sketched in Fig.1.An inverted microscope equipped with a high-speed camera is used to record the collective behavior of bacteria close to the drop edge, with the focal plane at the drop bottom.The visual field has a size of 696µm×695µm(with 0.34µm/pixel).As shown in the left panel of Fig.1,thexandyaxes represent the radial direction starting from the contact line and the tangential direction along the contact line,respectively.

Similar to the typical depiction of inertial turbulence,the formation of living turbulence within a wedge-shaped space exhibits numerous distinctive intermittent whirls and jets.To characterize this living turbulence,we perform the particle image velocimetry(PIV)analysis through the PIVlab module in MATLAB[34]to obtain the coarse-grained velocity field of the bacterial suspension,as shown in Fig.2.

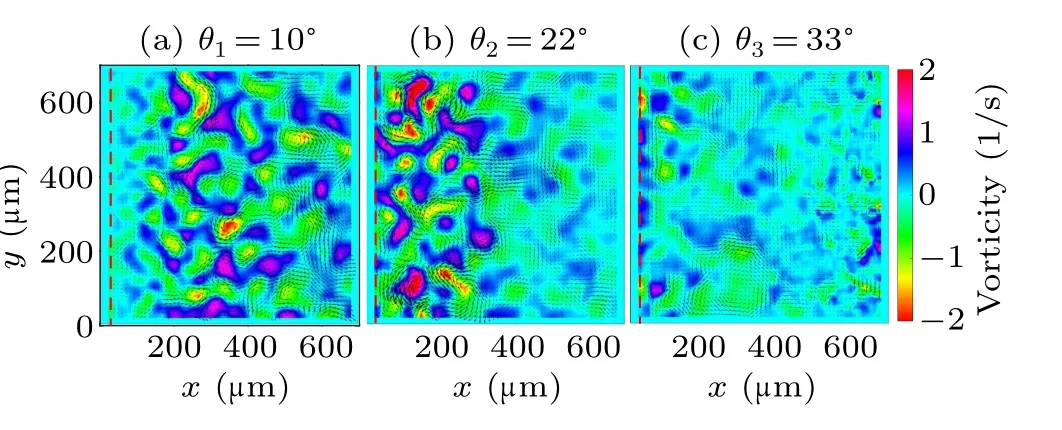
In particular, the vorticity map of the living flow shows an obvious non-uniform feature in the case ofθ2= 22◦(Fig.2(b)).Note that, the thickness of the wedge-shaped liquid film reduces to several micros at very close to the edge,which suppresses the motility of the swimming bacteria.In order to understand this heterogeneity, it is then necessary to further investigate the spatial distribution of the turbulent kinetic energy.By using the conventional way, the velocity is decomposed into a time averaged velocityv(r) and fluctuation velocityv′(r,t),where (·)denotes the average over time.The mean kinetic energyEm(r) and turbulent kinetic energyEt(r),are calculated from these two velocity components as

The distributions of turbulent kinetic energyEt(r) in three cases are shown in Figs.3(a)–3(c).It can be seen that the collective motion of bacteria is suppressed in the extremely thin liquid layer very close to the contact line,reflected by the much lower turbulent kinetic energy.Thereafter, the turbulent kinetic energy is more or less uniform distributed in the area away from the contact line in both cases of contact angleθ1=10◦andθ3=33◦.However, there is an obvious decay of turbulent kinetic energy in the case ofθ2,in the vicinity of 300µm away from the contact line.

Interestingly, a remarkable peak appears in the mean kinetic energy distribution in Fig.4(b)near the position 300µm away from the drop contact line withθ2= 22◦.Whereas,other distributions of mean kinetic energy are almost uniform(Figs.4(a) and 4(c)).Furthermore, we confrim that the peak value of mean kinetic energy results from the contribution of radial velocityvx, directing to the inside of the drop, as illustrated in Figs.4(d)–4(f).The gradient of the turbulent kinetic energy as ∇xEtcaptures the spatial variation ofEt.This dependence suggests that there is an inward mean flow from the contact line toward the drop center.This inward mean flow requires an outward counterpart above the observation layer(i.e.,the substrate bottom in the present work)to form a global circulation,which has been observed in Ref.[35].The turbulent kinetic energy presents a non-uniform distribution along the radial direction, which is intuitively ascribed to the varying thickness of the wedge-shaped drop corner.Then,we try to fgiure out the intrinsic reason responsible for the nonuniform fluctuation of turbulent energy.It is measured that the maximum variation of turbulence occurs at the distance aboutx=300µm away from the contact line,as shown in Figs.4(b)and 4(e).We confrim that this distance is stable around the whole drop by repetitively independent experiments.This characteristic distance corresponds to the local liquid height at that position,which establishes a vertical diffusion layer for oxygen.The bottom layer of the drop experiences a limited oxygen supply, whereas the air–liquid interface benefits from a rich oxygen source.

Considering the fact that the confined space at the drop corner can be approximately regarded as a triangle, and the thickness of the liquid filmhincreases with the distance from the contact line.It has been experimentally confirmed that persistent oxygen-consuming is needed to maintain the mobility of the bacteria and thus their collective motion.[36,37]It is also quantitatively determined for a accumulation layer of oxygenrich by combining oxygen diffusion and consumption,chemotaxis, and viscous fluid dynamics.[35]We have measured the active turbulence close to the air–liquid interface.The results show that an outward mean flux towards the contact line,which built a global circulation within this wedge-shape region close to the contact line.We believe that the increasing thickness of liquid film generates a non-uniformity of oxygen distribution,thereby affecting the activity of the bacteria.The dynamical evolution of the oxygen concentrationcwith the molecular diffusion coefficient ofDc, depends on the bacteria densityn,the consumption rateκof oxygen,and the fluid velocityvas[35]

2.2.Local anisotropic and global isotropic

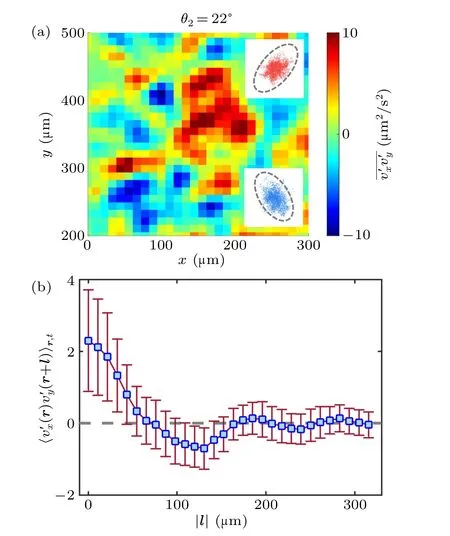
In the inertia turbulence, it is realistic anisotropic at the typical scale of the system since the energy is injected from the boundary.While well developed flow is normally regarded as isotropic which is also the essential basis of most statistical theories.[38–40]However, most theoretical and numerical studies for living turbulence also keep this isotropic hypothesis down to the unit-scale regime.[9]It has been shown that a longwavelength hydrodynamic instability drives the transition to form active turbulence.[41–43]In living turbulence, however,the isotropy or anisotropy is of great interest for evidence.Hence, the local anisotropy of living turbulence in our system is characterized at each node in the viscous feild,through the time-averaged product of turbulent velocitiesv′x·v′y.The red and blue spots in the map shown in Fig.6(a), represent locally anisotropic with nonzero velocity products and ellipselike asymmetry with opposite signs in the insets.Although it is locally anisotropic in the living turbulence system, the injected energy can be gathered to form collective motion at a much larger scale due to bacterial interactions.We thus analyze the spatiotemporal average of the correlation function of turbulent velocities in given distances.After considering and going through every velocity point in spatial and averaging on 500 frames (time of 10 s), a dependence that changes as the distance|l| increases has been presented in Fig.6(b).We find that the correlation function is non zero at short distances showing anisotropic properties and declines to a plateau around zero near 70µm which is in the order of typical size of collective motion.The analysis above reveals that the living turbulence is locally anisotropic due to energy generation at the unit scale and global isotropic at a much larger scale.

2.3.Energy spectrum and scaling

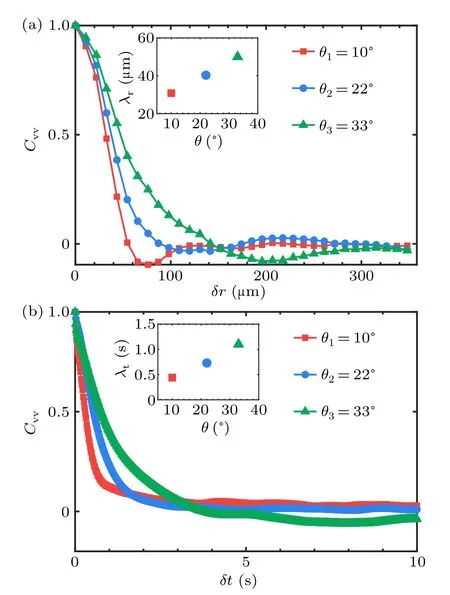
The structure of the swirling flow generated by the bacterial collective motion can be characterized by the velocity correlation functions which are calculated and plotted in Fig.7.The characteristic size and persistence time of the vortices are calculated to be∼50 µm and∼2 s as the order of magnitude,respectively.Turbulence exhibits a remarkable dynamical complexity characterized by vortices of varying sizes and random velocity fluctuations.Beneath the chaotic-like velocity field,a universal law called Kolmogorov-5/3 scaling has been found to govern the energy cascade in inertial turbulence.

Here, for the 2D living turbulence, the energy spectrumE(k)can be calculated by

whereRrepresents the position vector between two considered points andkis the scalar wavenumber with a value ofkldefined by the size of a single bacteria.〈·〉r,t,ψrepresents the average on the spatiotemporal domain and over the unit circle in wavenumber,respectively.Since the energy is injected in an anisotropic way from individual units,we thus check the onedimensional spectrum from the velocity componentsv′xandv′y,as explained in detail in the method section.We find that the 2D energy spectra of the turbulences can be roughly used for simplification as the overall energy spectra of the non-uniform living turbulence.Thek/kl∼1 donates the typical length scale of the unit for the energy injection, which is transferred into large vortices with the size of∼50µm(Fig.7)at a peak in the energy spectrum in Fig.8.In this region of large wavenumber,the averaged scaling varies from-1/5 to-1, depending on the geometric confinement of the systems.It seems that injected energy can be transferred with different efficiency into the vortices with the characteristic lengthλr∼50 µm due to collective motion,therefore showing herein different decaying slopes in the energy spectra.The sharper decrease (i.e.,k-1)in strong confinement (i.e.,θ=10◦) shows higher efficiency due to stronger bacterial alignment to form collective motion,than that in loose confniement (i.e.,θ=33◦).A robust scaling ofk1at the small wavenumber is found to be independent of detailed geometric confniement, which is consistent with result in Ref.[24].Note that the upper limit of the wavenumber is determined by the typical size of the individual bacteria(λl), which is not sufficiently smaller than the characteristic coherent length(λr)of the collective motion.Thus,as shown in Fig.8, calculating the energy scaling in the large range of wavenumber can not be across orders of magnitude.

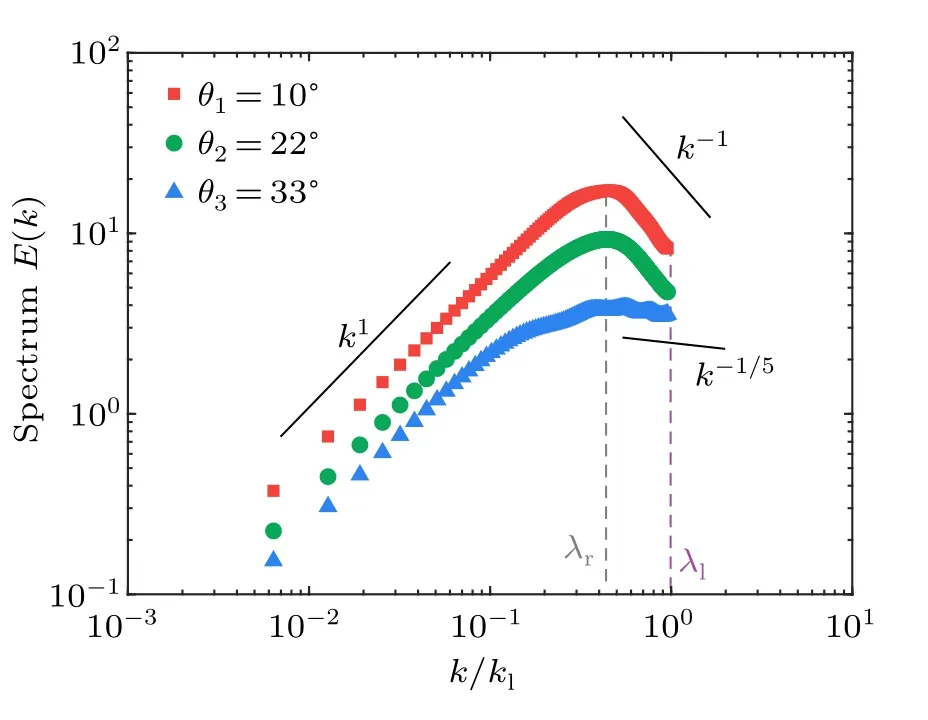
3.Conclusion

We construct spatial confinements featuring varying thickness gradients by manipulating the contact angle of sessile drops containing dense bacterial suspension.The diffusion-limited layer of oxygen from the air–liquid interface to the bottom of the drop creates a non-uniform oxygen concentration.The approximate cut-off distance of 100µm is estimated along the height direction,causing the heterogeneous distribution of bacterial activity along the radial direction of drop.The velocity fluctuation shows a large value close to the contact line where the oxygen is rich, while decays inward to the drop center where oxygen supply is significantly reduced due to the diffusion-limited regime across the thick liquid layer.Therefore non-uniform living turbulence is produced.Interestingly,energy is injected in a locally anisotropic way at the unit scale, but generates the isotropic feature at a much larger scale with energy spreading.The heterogeneous turbulence here is governed by the bacterial activity, thereby regulating a global flux of mean kinetic energy.This flux exhibits a linear dependence on the gradient of turbulent energy,analogous to the diffusion law.The bacterial activity can be controlled by the wedge-shaped geometry at the corner of a sessile drop.This natural non-uniform thickness of the liquid layer can tune the balance betweenExyandΩzwith a monotonic dependence by varying the contact angles of the bacterial drops.And the fniding suggests a potential strategy for controlling energy transfer through the deliberate design of non-uniform living turbulence.Furthermore, we perform a detailed analysis of the energy spectra, revealing a distinct scaling behavior for large wavenumbers ranging fromk-1/5tok-1.This scaling variation clearly demonstrates a pronounced dependence on the geometric confinement presents within the bacteria drops.We also characterize the energy spectra and show that the scaling for large wavenumber varies fromk-1/5tok-1, and this scaling behavior indicates a significant correlation with the geometric confinement presents within the bacterial drops.

4.Materials and method

4.1.Bacteria

The wild-type bacillus subtilis(strain 168)was used in all experiments.The bacteria were cultured using a standard protocol.In brief, the bacteria was taken out from a frozen tube stored at-20◦C,and then transferred into the Luria–Bertani broth (LB) medium in a plastic tube for overnight growth at 30◦C.Thereafter,a controlled volume of this bacterial suspension was picked and introduced to the new LB medium with a volume of 20 mL in a normal centrifugation tube, in order to keep the final optical density OD≈0.05 measured under the optical wavelength of 600 nm.Then the tube with the mixture of bacteria and medium was kept on a shaker at 30◦C with a shaking speed of 200 rpm for about 6 h.All the culture medium here of LB was made before the experiment from the components of tryptone 1.0%(w/v), yeast extract 0.5%(w/v),and NaCl 1.0%(w/v).The bacterial growth was stopped at the mid of the exponential phase.Then they were harvested and concentrated by centrifugation with the acceleration of 1500 g for 5 mins.After centrifugation, the clear upper supernatant was removed, and then the bacterial pellet was re-suspended into the motility buffer(MB).The MB medium was prepared with 0.01 M potassium phosphate, 0.067 M NaCl, and 10 M EDTA, and was adjusted to pH=7.0.The suspension was then washed twice by MB and diluted to the expected volume fractionφ(here∼7%, only accounting for volume occupation by the bacterial head body).The bacteria body length and radius were measured as≈4.0µm and≈0.5µm,respectively.Note that the volume fraction of bacteria was roughly calibrated asφ=0.001 corresponding to the bacterial number density ofn0=8×108cells/mL or OD600=1.0.

4.2.Experimental setup

We deposited 5 µL bacteria suspension onto a microscope quartz coverslip by a needle with inner diameter of 0.11 mm, to form a sessile drop.The coverslip and bacterial drop were together enclosed in an acrylic chamber loaded on the stage of the microscopy with saturated humidity and at room temperature (∼25◦C) to avoid the influence of evaporation as well as external disturbance.Images were recorded 3 min later than transfer process, in order that a steady state was sufficiently developed within the bacterial drop.An inverted microscope (Nikon Ti2-E, Japan) equipped with high speed camera(Hamamatsu,ORCA-Flash4.0 V3)was used for imaging in the bright-field mode.Two objective lens 20×(NA = 0.45) and 60× (NA = 1.2) were used to obtain the view-filed with size about 696µm×695µm(0.34µm/pixel)and 225µm×225µm,respectively.The frame rate was fixed to be 50 fps with resolution of 2048 pixels×2044 pixels.All snapshots and video stacks were focused on the bottom of the coverslip, which was defined asx–yplane in our coordinate system.No evaporation flow was observed in our experiments.The observation window was located in the region near the contact line of the bacterial drop.

4.3.Image processing and data analysis

The continuous image sequences taken by bright-field microscopy,stored the signal intensity of the whole field,which reflected the movement of the coarse-grained flow generated by dense swimming bacteria.The imaging here was difficult for particle-resolved tracking but favored the measurement of the velocity field.This velocity field could be obtained by the analysis routines of PIVlabs in MATLAB based on the raw videos.The key parameters, window size and step size,were set as 128 pixels and 32 pixels respectively for all of our PIV processes.Then, the optimal interrogation window size was calibrated as 43.52 µm by 43.52 µm, for each pair of neighboring frames.Other parameters were set to be default values.The minimum lattice spacing of the velocity field was 10.88µm.The velocity field in Fig.1 shows the velocity vectors at each lattice.To verify the accuracy of PIV measurements,we also carried out particle tracking velocimetry(PTV)by adding passive colloidal tracers (1 micrometer of diameter, red fluorescence-labeled, Fluoro–Max, thermo scientifci)in bacterial suspensions.The radial velocity distributionvxshows similar results by using both PIV and PTV(Fig.9),displaying a maximum velocity band located aroundx=300µm.

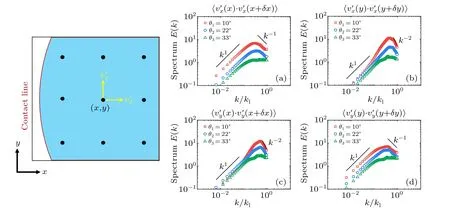
The energy spectraE(k)quantify the energy distribution over different length scalesλ=2π/k, wherekis the wave number.Here, the energy spectrum is obtained by calculating the Fourier transform of the two-point velocity correlation function〈v(r0)·v(r0+δr)〉,averaging over the spatiotemporal domain and the unit circle in wavenumber space.Here,we check the one-dimensional energy spectra in separate directions except for energy distribution with respect to the scalar wavenumber by averaging around the unit circle.We calculate the turbulent velocity componentsv′xandv′yalongxandyaxes as〈v′x(x)·v′x(x+δx)〉,〈v′x(y)·v′x(y+δy)〉,〈v′y(x)·v′y(x+δx)〉and〈v′y(y)·v′y(y+δy)〉,as shown in Fig.10.We can see that scaling of radial velocity along the radial direction,has the same scaling as that of the total spectrum with scalar wavenumber calculated from 2D velocity.Therefore, the 2D energy spectra of the turbulences can be roughly used for simplification as the overall energy spectra of the non-uniform living turbulence.

Acknowledgments

Project supported by the National Natural Science Foundation of China(Grant Nos.12174306 and 12004308)and the Natural Science Basic Research Program of Shaanxi (Grant No.2023-JC-JQ-02).The authors also thank D.Saintillan,A.Lindner,and X.Shi for useful discussions and contributive suggestions.