Optical image encryption algorithm based on a new four-dimensional memristive hyperchaotic system and compressed sensing

Yang Du(都洋), Guoqiang Long(隆国强), Donghua Jiang(蒋东华) ,Xiuli Chai(柴秀丽),†, and Junhe Han(韩俊鹤),‡

1Center for Physics of Low-Dimensional Materials,Henan Joint International Research Laboratory of New Energy Materials and Devices,School of Physics and Electronics,Henan University,Kaifeng 475004,China

2School of Artificial Intelligence,Henan Engineering Research Center for Industrial Internet of Things,Henan University,Zhengzhou 450046,China

3School of Computer Science and Engineering,Sun Yat-sen University,Guangzhou 510006,China

Keywords: memristor,hyperchaotic system,compressed sensing,fractional Fourier transform,optical image encryption

1.Introduction

With the rapid development of the Internet,artificial intelligence technology is more and more closely connected with people’s lives,[1–6]and different types of data can be rapidly disseminated and diffused through the network, in which the issue of image information security has become more and more serious.[7–9]In order to address the above issues, some image encryption schemes have been proposed.

Fridrich[10]first applied chaotic maps for image encryption in 1997.After that, some simple one-dimension (1D)chaotic maps[11–15]were widely proposed by scholars and applied to the field of image encryption.However, the security of 1D chaotic map is low because of its small key space and vulnerability to violent attacks.Therefore,in order to improve the shortcomings of 1D chaotic map,some scholars have provided image encryption algorithms based on high-dimensional chaotic map by improving 1D chaotic map.[16–18]Because of the excellent nonlinear characteristics of memristor, some scholars applied it for chaotic maps to produce systems with stronger chaotic characteristics.Liet al.[19]designed an image encryption algorithm combining memristor and chaotic tent map.Wanget al.[20]presented a new hyperchaotic system with two memristors as nonlinear terms in the system.Yeet al.[21]proposed an image encryption scheme based on seven-order hybrid memristive chaotic circuit.Penget al.[22]designed a new memristor chaotic circuit based on Lorenz-like circuits and applied it to image encryption.Memristor chaotic systems have great application value in the field of image encryption, so it is urgent and necessary to continue to explore and study memristor chaotic systems with more complex dynamic behavior.

Images have the characteristics of large amount of data and high information redundancy.In order to remove the redundant information of images and improve the transmission and storage efficiency of algorithms,scholars applied the theory of compressed sensing[23]to the image encryption process, and proposed some image encryption algorithms based on CS.Xuet al.[24]constructed two measurement matrices to measure the image from two directions, so as to obtain better compression performance with higher efficiency.Zhouet al.[25]proposed an image encryption algorithm based on CS and fractional Mellin transform.Yanget al.[26]constructed the measurement matrix through the fractional hyperchaotic system, and introduced the DNA coding technology into the encryption process,which improved the complexity and security of the algorithm.Zhouet al.[27]used two-dimensional (2D)CS to compress and encrypt images and cyclic shift to improve the security of the algorithm.Although CS is introduced into the above scheme, the image reconstruction quality is poor and the robustness of the algorithm cannot be guaranteed.Therefore, the design of a robust CS encryption algorithm has attracted attention.[28,29]Luoet al.[30]constructed a measurement matrix by Lissajous map and logistic map, and designed an encryption algorithm with strong robustness.Zhanget al.[31]put forward a robust image compression–encryption scheme, which uses 2D projection gradient algorithm for image reconstruction,but the security of the algorithm is lacking.Therefore,it is necessary to design a compression–encryption algorithm with both robustness and security.Based on the previous discussion of image encryption algorithms based on CS, it is worth noting that while some algorithms have used CS to achieve efficient image compression,the trade-off is reduced image quality and potential security vulnerabilities in the encryption process.[32–34]This has led to a growing interest in designing image encryption algorithms that balance robustness and security.One approach that has gained attention is the use of optical encryption methods, such as the double random-phase encoding algorithm.

In 1995, Refregieret al.[35]first proposed an optical image encryption algorithm based on double random-phase encoding (DRPE).Optical transformation has its unique highspeed parallel data processing ability and multi-dimensional coding space.[36]Optical image encryption algorithms based on DRPE and different optical transformations have been widely proposed.The authors in Refs.[37–40] applied different optical transformations to realize image encryption in DRPE, such as fractional wavelet transform, Hartley transform, fractional Fourier transform, fractional Mellin transform, and so on.However, since DRPE is a linear system,the corresponding image encryption is vulnerable to knownplaintext and chosen-plaintext attacks.Fortunately,the nonlinearity of chaotic systems can compensate for the lack of nonlinearity of DRPE.Some algorithms[41–43]combined chaotic system with DRPE to improve the security of the algorithm,but these algorithms generally used a single integer-order chaotic system, and the key space was small.The authors in Refs.[44,45]proposed some optical encryption algorithms combining DRPE with CS.However, these algorithms have not been comprehensively analyzed,so their security needs to be verified.

Recently,Jianget al.[2]proposed a cross-ring neural network model based on the Hopfield neural network to reduce bandwidth saturation in communication channels and securing the transferred medical data.Yuet al.[3]constructed a 4D memristive Hopfield neural network (MHNN) which can perform complex dynamics and performs well in image encryption applications for the significant complexity of multiscroll.Suet al.[4]proposed a multi-image visual encryption algorithm based on region of interest(ROI)to ensure the security of multiple image regions of interest.This design scheme can not only reconstruct the significant part without damage,but also reduce the storage space.

Generally speaking, despite being powerful already, the current image encryption schemes suffer from the following problems:

(i)Most of image encryption schemes adopt simple lowdimensional chaotic systems,which have small key space and chaotic interval,and thus they are vulnerable to violent attacks and have insufficient security.

(ii)In some CS-based schemes, the measurement matrix is a random Gaussian matrix,and the whole measurement matrix needs to be transmitted and stored as a key when decrypting,which takes up a lot of transmission bandwidth and storage space.

(iii) Although some schemes use chaotic sequences to construct deterministic measurement matrices, most of them use a single chaotic system.The parameters and initial values of chaotic systems are simple and fixed,and the performance of the constructed measurement matrices is poor, the quality of image reconstruction is not high,and the robustness of the algorithm is unsatisfactory.

(iv)Some schemes are not related to plaintext images,and are hence vulnerable to known-plaintext and chosen-plaintext attacks.

In order to solve the problems in the above schemes,this paper proposes a new image encryption scheme based on 4D MHS,CS,and DRPE.The main contribution of the proposed scheme is as follows:

(I) A new 4D MHS is designed, which generate four hyperchaotic sequences simultaneously.The structure of 4D MHS is simple and easy to implement.The results show that 4D MHS has a larger key space, richer dynamical behavior,and more complex hyperchaotic properties.

(II)A method of constructing deterministic chaotic measurement matrix(DCMM)is proposed by combining 4D MHS and 1D CCS.The system parameters and initial values of 1D CCS are determined from four hyperchaotic sequences of 4D MHS,in which the system parametersuiandviare no longer fixed values and will change in each iteration,which improves the randomness of the DCMM.Compared with other commonly used random measurement matrices,using the DCMM can not only save a lot of transmission bandwidth and storage space,but also ensure the quality of image reconstruction.

(III) The proposed scheme combines 4D MHS, CS, and DRPE.The introduction of CS reduces the amount of image data and reduces the transmission burden of hardware devices.DRPE has unique high-speed parallel data processing ability and multi-dimensional coding space ability,and the excellent hyperchaotic characteristics of 4D MHS can make up for the lack of nonlinearity of DRPE.Among them,the optical transformation adopts fractional Fourier transform,which increases the key space of the algorithm and improves the security of the algorithm.

(IV)The confusion method and the diffusion method are proposed.The confusion and diffusion process needs row keykrand column keykc, which are closely related to plaintext images.Four hyperchaotic sequences are used in the construction process of the DCMM, DRPE, confusion and diffusion process,and the generation of hyperchaotic sequences is determined by the hash value of plaintext images and external keys.The proposed algorithm is sensitive to plaintext images and can effectively resist known-plaintext and chosen-plaintext attacks.

The rest of this paper is organized as follows: In Section 2, the preliminaries of the work are described.In Section 3,the specific process of image encryption and decryption in this scheme is introduced in detail.In Section 4,simulation results and performance analyses are provided.In Section 5,our work is summarized.

2.Preliminaries

2.1.One-dimensional Chebyshev–Chebyshev system (1D CCS)

The one-dimensional CCS[13]is a new chaotic map constructed by the difference between the output sequences of two 1D Chebyshev chaotic maps.Compared with 1D Chebyshev chaotic map,the 1D CCS has better chaotic characteristics and larger chaotic interval.Its mathematical expression is

where the system parameteru ∈(0,10],v ∈[8,20], and the initial value of the system iss0.

2.2.Compressed sensing(CS)

Donohoet al.[24]put forward compressed sensing theory in 2006.The CS pointed out that if the signal is sparse or sparse in a transform domain, the high-dimensional signal can be projected into the low-dimensional space through the measurement matrix independent of sparse basis,and then the original signal can be recovered more accurately by solving the convex optimization problem.

Assume that the signalxN×1isK-sparse and transforms it under the standard orthogonal baseΨ.

There are onlyK(K ≪N)non-zero coefficients in the vectors.The original signal is projected by using the measurement matrixΦM×Nindependent ofΨ,which is expressed as

M(M ≪N)linear measurementsycan be obtained,which already contain enough information for reconstructing the signalx,andycan be expressed as

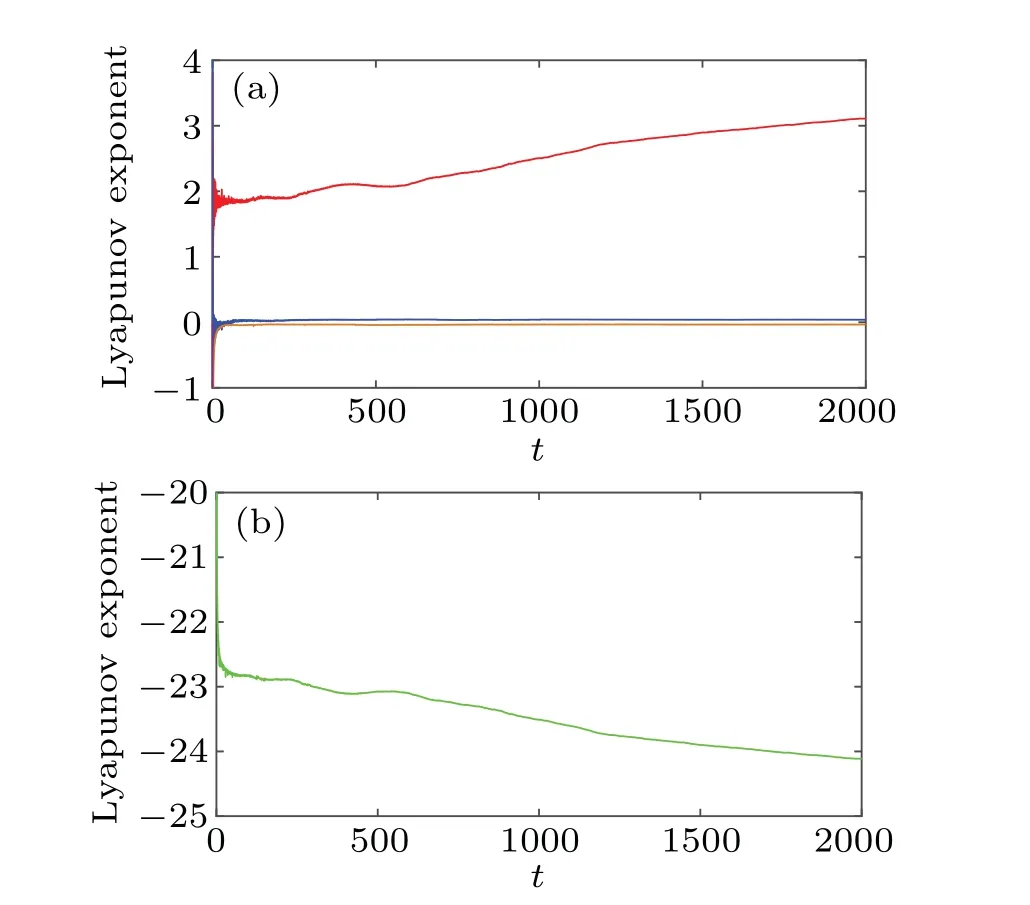
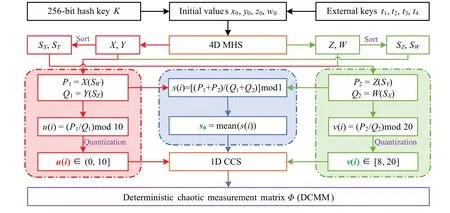
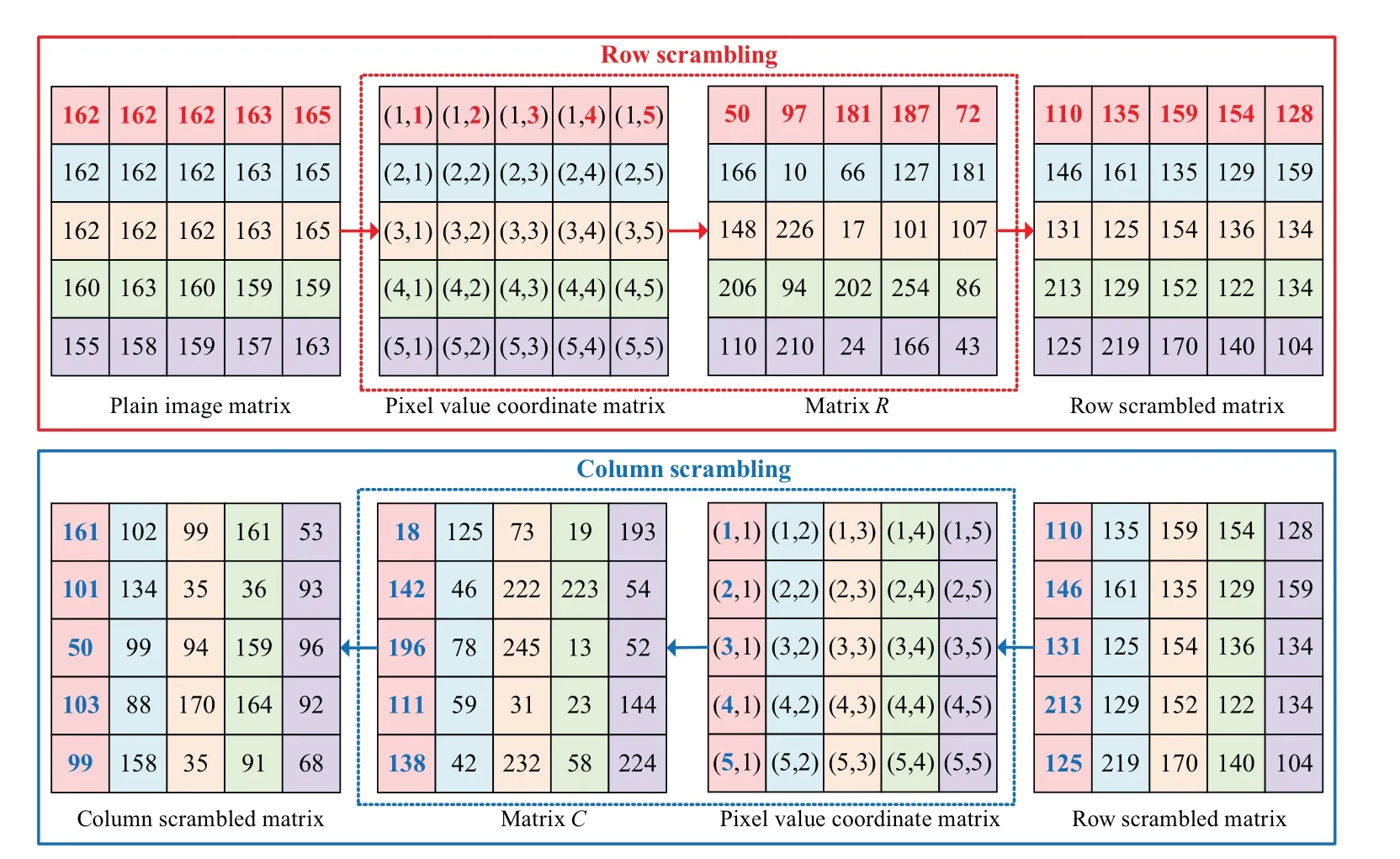
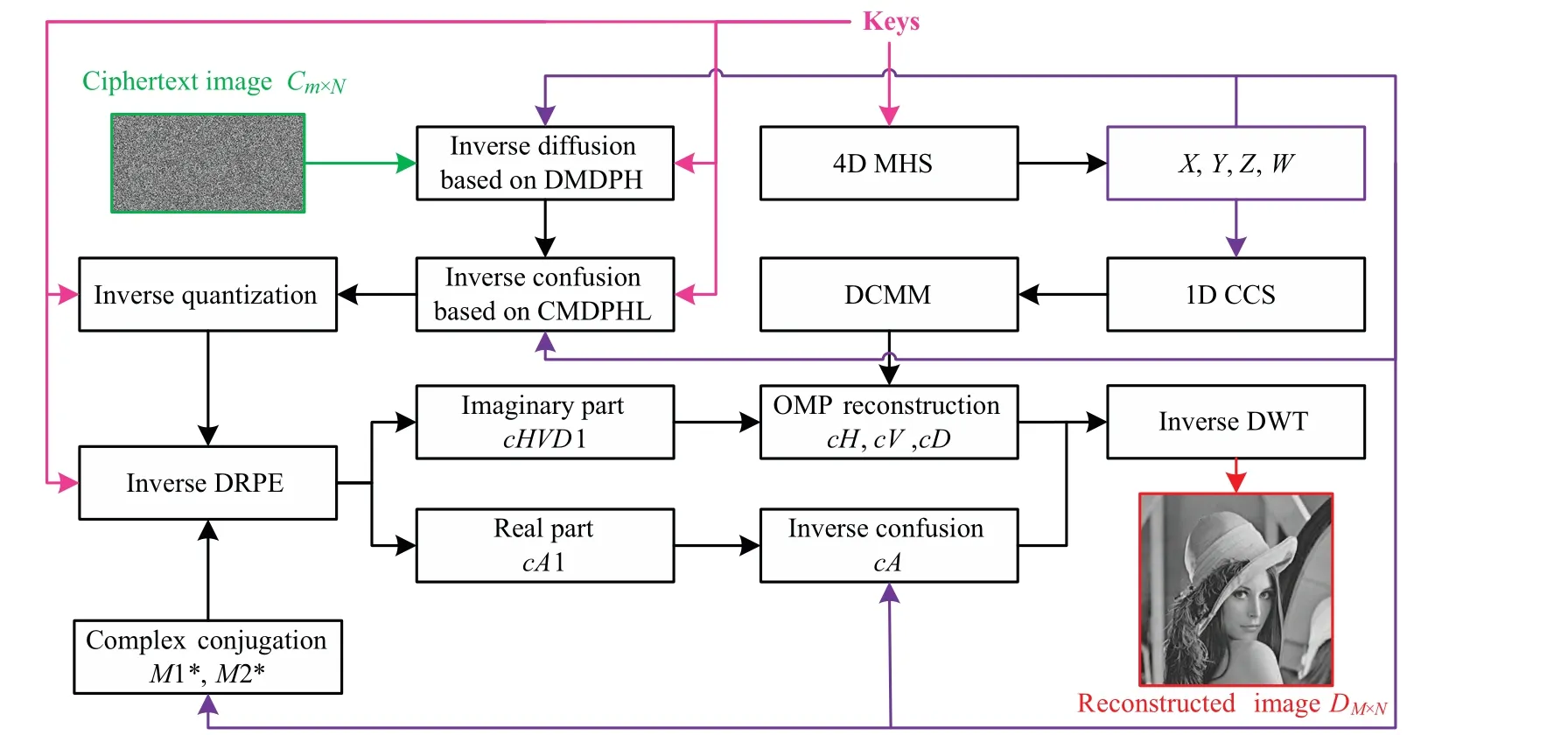
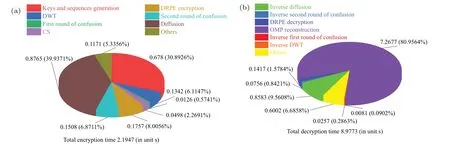
whereΘis sensing matrix,xis reconstructed by solving the optimal problem, and the convex optimization problem is solved by using the minimumlp(0

where||s||pis thelpnorm of the vectorsand the measurement matrixΦM×Nhas to satisfy the restricted isometry property (RIP).The original signalxcan be recovered from the dimensionality reduction process.At present, there are many reconstruction algorithms,such as basis pursuit(BP),orthogonal matching pursuit(OMP),smoothedl0norm(SL0),and so on.

2.3.Fractional Fourier transform(FrFT)

In 1980,Namias first put forward the definition and properties of fractional Fourier transform.[46,47]In 1987, Mcbride and others perfected the concept of Namias, and they gave a strict mathematical definition of the fractional Fourier transform.[48]The integral form of the fractional Fourier transform of the functionf(x)is

wherekα(x,u)is its kernel function and its state equation is

2.4.Latin square

Latin square[49]is ann×nsquare matrix.In then×nsquare matrix,there are exactlyndifferent elements,and each different element only appears once in each row or column.Figure 1 gives four examples of Latin square matrix with different orders.The pseudo-code for generating the Latin square matrix[50]is shown in Algorithm 1.Here sort(x) is a sort function, which sorts the sequencexin ascending order.The circshift(x,y)means to cyclically move the sequencexfrom left to right byypositions.

Fig.1.Latin square example.(a)2×2,(b)3×3,(c)4×4,(d)5×5.

Algorithm 1: A Latin square matrix generation method Input: Q1 and Q2 are two sequences of equal length(N)Output: L is a Latin square of order N 1 Qseed=sort(Q1);2 Qshift=sort(Q2);3 for i=1:N do 4 L(i,:)=circshift(Qseed,Qshift(i));5 end for

3.The proposed image encryption and decryption scheme

3.1.The new 4D memristive hyperchaotic system (4D MHS)

In this section,a new 4D memristive hyperchaotic system is proposed.By introducing a quadratic memristor model.[51]into a three-dimensional (3D) Lorenz-like chaotic system, a 4D chaotic system fed back by the memristor is obtained.After that, the performance analysis of the new system proves that it has excellent hyperchaotic characteristics.The memristor model is shown below:

whereqis the charge,ϕis the magnetic flux,α,βare positive real numbers, andW(ϕ)is the memristor function of the quadratic magnetron memristor model.

3.1.1.Mathematical model

The mathematical model of the 4D MHS can be defined by

wherea,b,care the control parameters of the system,x,y,z,ware the state variables of the system,kis the coefficient associated with the memristor.

3.1.2.Phase–orbit diagram

The phase–orbit diagram of chaotic attractor is the motion trajectory of the system,which reflects the change in the motion state of the system.When the chaotic attractor appears in the phase space, it can be roughly considered that the system has chaotic behavior.

Fig.2.Phase–orbit diagrams of 4D MHS:(a)x–y–z space,(b)x–y plane,(c)x–z plane,(d)y–z plane.

When the system parameters are set toa= 35,b= 6,c=20,k=6,α=0.1,β=0.02, and the initial values of the system are set tox0=10,y0=10,z0=10,w0=10, the phase–orbit diagram of the system is shown in Fig.2.It can be seen that there are two chaotic attractors in the phase space,which have complex folding and stretching trajectories,ergodicity and boundedness in a specific attraction domain,and the dynamic behavior is complex.So the system can be considered to be in a chaotic state.

3.1.3.Analysis of system dissipation

The trajectory of a chaotic system has the characteristics of contraction and divergence at the same time.The contraction of the trajectory makes the system dissipative, while the local instability of the trajectory makes the system divergent.When the system is dissipative,it can converge to a finite set,which indicates that the system is bounded.

The dissipative analysis of the system is carried out to judge whether the system converges, and the certainty and global stability of the system can be analyzed theoretically.The divergence expression of the system can be derived from Eq.(11):

Under the conditions of system parameters and initial values set in Subsection 3.1.2, the divergence of the system can be calculated by Eq.(12)as ∇·V=-a+c-b=-35+20-6=-21.Because ∇·V=-21<0,the system is dissipative and converges at e-21tspeed.

3.1.4.Analysis of system equilibrium points and stability

It is generally believed that chaotic systems need at least one unstable equilibrium point.In order to solve the equilibrium point of the system, let the right side of the system equations defined by Eq.(11)be equal to zero,and under the above parameters,the equilibrium point of the system is point setP={x=y=z=0,w=C}, whereCis any real number.It can be seen that there are infinitely many equilibrium points in the system at this time.

Taking the equilibrium pointO={x=y=z=w=0}as an example to analyze whether the system is stable at this equilibrium point,the Jacobian matrix of the system at the equilibrium pointOis

Assuming thatλis the eigenvalue andIis a fourth-order identity matrix,four eigenvaluesλ1=19.6155,λ2=0,λ3=-6,andλ4=-34.6155 of the system can be obtained by solving determinant|λI-J|=0.

Because the eigenvalue of the system is a positive real root,a zero root,and two negative real roots,according to the Routh–Hurwitz stability criterion,the system is unstable at the equilibrium pointO.Therefore,the system has at least one unstable equilibrium point.

3.1.5.Analysis of system Lyapunov exponent and dimension

Lyapunov exponent is an important quantitative index to measure the chaotic characteristics of the system, which represents the average exponential rate of convergence or divergence between adjacent orbits in the phase space.

Every dimension of a chaotic system has a corresponding Lyapunov exponent.If the system has only one positive Lyapunov exponent, it indicates that the system is a chaotic system.If the system has two or more positive Lyapunov exponents,it shows that the system is hyperchaotic,with two or more trajectory separation directions,and its dynamic behavior on the trajectory is more complex and hyperchaotic.

Fig.3.Lyapunov exponents diagram of the 4D MHS: (a) exponents diagram of L1,L2,and L3,(b)exponents diagram of L4.

Under the conditions of the above system parameters and initial values, we solve the Lyapunov exponent of the system by the Jacobian matrix method,as shown in Fig.3.The Lyapunov exponents of the system areL1=3.1104,L2=0.0392,L3=-0.0350,andL4=-24.1146.The system has two positive Lyapunov exponentsL1andL2, and the sum of all Lyapunov exponents is less than zero, so the system is in hyperchaotic state.

The Lyapunov dimension is calculated by Eq.(14), and the Lyapunov dimensionDL=3.1292 is a fractional order,which indicates that the system has a more complex fractal structure.

3.1.6.Effect of parameter changes on system dynamics

System parameters have a very important influence on the dynamic behavior of chaotic systems.Keeping other parameters unchanged,taking the parameterbas a variable,with the change of parameterbin the interval [0, 8], the bifurcation diagram of system state variablexand the Lyapunov exponents diagram of the system are shown in Fig.4.It can be seen that when the parameterbchanges, the system presents a variety of motion states,and its motion states correspond to the Lyapunov exponents diagram.Whenb ∈[2,8],the system has two positive Lyapunov exponents, and the system is in a hyperchaotic state.

3.1.7.Analysis of the NIST SP800-22 standard test

Currently,the most well-established standard for evaluating the randomness of sequences is the NIST SP800-22 standard test, which has 15 tests.If the test result isP-value>0.01,the sequence passes the test.

In order to further analyze the performance of the 4D MHS, four hyperchaotic sequencesX,Y,Z,Ware tested by the NIST SP800-22 standard, and the results are shown in Table 1.It can be seen that all hyperchaotic sequences have passed the NIST SP800-22 standard test,which shows that the 4D MHS has excellent hyperchaotic characteristics, and the hyperchaotic sequences generated by it are safe enough for image encryption.

Fig.4.(a)Lyapunov exponents diagram of the system varying with the parameter b,(b)bifurcation diagram of system state variable x varying with the parameter b.

3.2.Construction method of deterministic chaotic measurement matrix

In this section, a method of constructing deterministic chaotic measurement matrix (DCMM) is proposed based on 4D MHS and 1D CCS.Compared with some commonly used random measurement matrices that require the entire measurement matrix to be stored and transmitted as the key, DCMM only requires the 256-bit hash keyKassociated with the plaintext image and the external keysti(i=1, 2, 3, 4).It can effectively reduce the space consumption during key storage and transmission,and also ensure good image reconstruction quality.

Set the compression rate CR=0.5, the size of plaintext imagePisM×N,and the size of DCMM ism×n(m=M/2,n=N/2).The construction process of DCMM is shown in Fig.5,and the specific steps are as follows:

Step 1 The 256-bit hash keyKof the plaintext imagePM×Nis calculated,andKis converted into thirty-two decimal numberski(i=1, 2,..., 32) in groups of eight.The initial valuesx0,y0,z0,w0of the 4D MHS are generated bykiand the external keysti,as shown below:

where⊕indicates the XOR operation, ∑indicates the summation operation,mod()indicates the remainder operation.

Step 2 The initial valuesx0,y0,z0,w0are brought into the 4D MHS and iteratedm×n+N0times.To avoid transient effects,the firstN0(N0=1000)values are discarded and four hyperchaotic sequencesX,Y,Z,Wof size 1×mnare obtained, which are arranged in ascending order to obtain four index sequencesSX,SY,SZ,SW.The index sequencesSX,SY,SZ,SWare used to permute the sequencesX,Y,Z,Wto obtain sequencesP1,Q1,P2,Q2in turn.

Step 3 The sequences of system control parametersui,vi(i=1,2,...,m×n)and the initial system values0of the 1D CCS are generated from the sequencesP1,Q1,P2,Q2as shown below:

Given that the control parametersu ∈(0,10],v ∈[8,20], the sequencesuiandviare quantized into the above intervals.

Step 4 The sequenceui,viand the initial values0are brought into the 1D CCS and iteratedm×ntimes to obtain the chaotic sequencesi(i=1, 2,...,m×n).The sequencesiis rearranged into a matrixΦof sizem×n, as shown in Eq.(19).The matrixΦm×nis the DCMM.The system control parametersui,vichange in each iteration,which enhances the randomness of DCMM.

where reshape(s,m,n)indicates the rearrangement of the sequencesinto a matrix with a size ofm×n.

Fig.5.The construction process of DCMM.

3.3.Confusion method determined by plaintext information,hyperchaotic sequences,and Latin square matrix(CMDPHL)

In this section,a confusion method based on the plaintext information,hyperchaotic sequences,and Latin square matrix is proposed to determine the confusion matrix.First, the row keykrand the column keykcare generated from the plaintext imagePM×N.Then, the Latin square matrixLm×nis generated from the hyperchaotic sequencesX,Yaccording to the method in Subsection 2.4.Finally,the row scrambling matrixRm×nand the column scrambling matrixCm×nare generated fromkr,kc,Lm×n,and hyperchaotic sequencesZ,W.The matrixP1m×nis permuted byRm×nandCm×n.The specific steps are shown as follows.

Step 1 Calculate the information entropyHpof the plaintext imagePM×N.Seek the maximum valuermaxand the minimum valuerminfor the sum of the row pixel value ofPM×N.Similarly, find the maximum valuecmaxand the minimum valuecminfor the sum of column pixel values.Calculate the row keykrand the column keykcfrom

where floor(x) indicates taking the largest integer not greater thanx.

Step 2 The four hyperchaotic sequencesX,Y,Z,Wof size 1×mngenerated in Subsection 3.2 are quantized in the interval[0,255].

Step 3 The sequencesXandYare used to generate the Latin square matrixLm×naccording to the method in Subsection 2.4.

Step 4 The row confusion matrixRm×nis generated by the row keykr,the Latin square matrixLm×nand the sequenceZtogether,as shown below:

Step 5 The column confusion matrixCm×nis generated by the column keykc, the Latin square matrixLm×nand the sequenceWtogether,as shown below:

Step 6 Each row of matrixP1m×nis scrambled by matrixRm×nand each column of matrixP1m×nis scrambled by matrixCm×nto obtain the scrambled matrixP2m×n.

The pseudo-code of the scrambling algorithm is shown in Algorithm 2, and the procedure of the scrambling method is illustrated in Fig.6.

Algorithm 2: The confusion method based on CMDPHL Input: matrix P1;size of P1: m,n;hyperchaotic sequences X,Y,Z,W;the row key kr;the column key kc Output: the scrambled matrix P2m×n 1 X =floor(mod(X×1014,m));Y =floor(mod(Y×1014,m));Z=floor(mod(Z×1014,m));W =floor(mod(W×1014,m));2 P=P1;3 [∼,SX]=sort(X);[∼,SY]=sort(Y);4 for i=1:m do 5 L(i,:)=circshift(SX,SY(i));6 end for 7 for i=1:m do 8 for j=1:n do 9 R(i,j)=mod(kr+L(i,j)+Z(i),m)+1;10 P(i,j)=P(i,R(i,j));11 end for 12 end for 13 for i=1:m do 14 for j=1:n do 15 C(i,j)=mod(kc+L(i,j)+W(i),n)+1;16 P(i,j)=P(C(i,j),j);17 end for 18 end for 19 P2=P;

Fig.6.The process example of the confusion method based on CMDPHL.

3.4.Diffusion method determined by plaintext information and hyperchaotic sequences(DMDPH)

In this section,a diffusion method based on plaintext information and hyperchaotic sequence is proposed to determine the diffusion matrix.The pseudo-code of the diffusion algorithm is shown in Algorithm 3.The specific steps of the diffusion algorithm are as follows:

Step 1 The quantized sequencesXandYof size 1×mnare rearranged into a matrixAof sizem×N,and similarly,the matrixBm×Nis obtained from the sequencesZandW.

Step 2 The row keykrand the matrixAm×Njointly determine the forward diffusion of the pixel values of the matrixP1m×N,and the matrixHm×Nis obtained,as shown below:

Step 3 The column keykcand matrixBm×Njointly determine the inverse diffusion of the pixel values of the matrixHm×N, and the matrixVm×Nis obtained, which is the matrixP2m×Nafter diffusion,as shown below:

Algorithm 3: The diffusion method based on DMDPH Input: matrix P1;size of P1: m,N;hyperchaotic sequences X,Y,Z,W;the row key kr;the column key kc Output: the diffused matrix P2m×N 1 A=[X,Y];A=reshape(A,m,N);2 B=[Z,W];B=reshape(B,m,N);3 P=P1;4 for i=1:m do 5 for j=1:N do 6 if(i=1)&(j=1)7 H(i,j)=bitxor(bitxor(P(i,j),kr),A(i,j));8 else if(i ≥2)&(j=1)9 H(i,j)=bitxor(bitxor(P(i,j),P(i-1,N)),A(i,j));10 else 11 H(i,j)=bitxor(bitxor(P(i,j),P(i,j-1)),A(i,j));12 end if 13 end for 14 end for 15 for j=N:-1:1 do 16 for i=m:-1:1 do 17 if(i=m)&(j=N)18 V(i,j)=bitxor(bitxor(H(i,j),kc),B(i,j));19 else if(i=m)&(j

3.5.Encryption process

The flow chart of the proposed image encryption algorithm in this paper is shown in Fig.7.It consists of three main stages: CS-based encryption stage, optical encryption stage based on FrFT,and confusion and diffusion stage.

In the CS-based encryption process, the measurement matrix used is the DCMM proposed in Subsection 3.2; the confusion method is CMDPHL elaborated in Subsection 3.3;and the diffusion method is DMDPH proposed in Subsection 3.4.The specific steps are shown below.

Step 1 Input the plaintext imagePM×Nand set the compression rate as CR=0.5.Calculate the 256-bit hash keyKofPM×Nby the SHA-256 function,and generate the initial valuesx0,y0,z0,w0of 4D MHS by use ofKand the external keysti.Obtain four hyperchaotic sequencesX,Y,Z,Wof size 1×mnfrom 4D MHS.Construct theΦm×nfrom the sequencesX,Y,Z,W, and 1D CCS.The specific steps are shown in Subsection 3.2.

Step 2 The discrete wavelet transform (DWT) is performed on the plaintext imagePM×Nto obtain the approximation coefficients matrixcAm×nand detail coefficients matricescHm×n,cVm×n,cDm×n.The“haar wavelet”is chosen,and the detailed process is shown below:

Step 3 Scramble the matrixcAm×nby the sequencesX,Y,Z,Wto obtain the matrixcA1m×n, as shown in Eq.(27).The matrixΦm×nis divided into the matricesΦcH(m/2×n),ΦcV(m/4×n),ΦcD(m/4×n), and the matricescHm×n,cVm×n,cDm×nare compressed and measured in turn to obtain the matricescH1(m/2×n),cV1(m/4×n),cD1(m/4×n), as shown in Eq.(28), where the matrixψis the sparse basis of DWT and the matrixψTis the transpose matrix of matrixψ.

Step 4The matricescH1(m/2×n),cV1(m/4×n),cD1(m/4×n)are combined into a matrixcHVD1m×n.The matrixcA1m×nis used as the real part and the matrixcHVD1m×nis used as the imaginary part, and the above two are combined into a complex matrixcAHVDm×n, as shown in Eq.(29).The random phase masksM1m×n,M2m×nare generated by the sequencesX,Y,Z,W, as shown in Eq.(30).The DRPE encryption is manipulated on the complex matrixcAHVDm×nto obtain the complex matrixcAHVD1m×n,and the optical transform is the fractional Fourier transform,as shown in Eq.(31):

whereFt3Ft4()is the fractional Fourier transform with ordert3in thexdirection and ordert4in theydirection,tiis the external key.

Step 5The real part of the complex matrixcAHVD1m×nis taken to obtain the matrixcA2m×n; the imaginary part is taken to obtain the matrixcHVD2m×n.The element values of the matricescA2m×n,cHVD2m×nare quantized into the interval[0,255]to obtain the matricescA3m×n,cHVD3m×n,as shown below:

whereAmaxindicates the maximum element in matrixA,Aminindicates the minimum element in matrixA,real(A)indicates taking the real part of the matrixA, imag (A) indicates taking the imaginary part of the matrixA,round(x)indicates the integer rounded to the nearestx.

Step 6The matricescA3m×nandcHVD3m×nare scrambled by CMDPHL to obtain matricescA4m×nandcHVD4m×n.The specific steps are shown in Subsection 3.3.Combine the matricescA4m×nandcHVD4m×ninto a matrixcAHVD2m×N,as shown below:

Step 7The matrixcAHVD2m×Nis diffused by DMDPH to obtain the matrixcAHVD3m×N,which is the ciphertext imageCm×N.The specific steps are shown in Subsection 3.4.

Fig.7.The flow chart of the proposed image encryption algorithm.

3.6.Decryption process

The decryption algorithm is the inverse process of the encryption algorithm,and the flow chart of the decryption algorithm is shown in Fig.8.The 256-bit hash keyK, the external keysti(i=1, 2, 3, 4) and the intermediate keyscA2min,cA2max,cVHD2min,cVHD2max,krandkcneed to be transmitted to the receiver for decryption.The OMP algorithm is chosen for the image reconstruction method.The specific steps of the decryption algorithm are not described here.

Fig.8.The flow chart of the proposed image decryption algorithm.

4.Experimental simulation and security analysis

In this section,the proposed image encryption scheme is simulated, and the simulation results and the security performance of the algorithm are analyzed.The simulation environment used is in a personal computer with an Intel(R)Core(TM) i5-6300HQ 2.30 GHz CPU and 8 GB memory, the operating system is Microsoft Windows 11,64-bit,and the software is Matlab2016b.

The fixed parameters used in the experimental simulations are the external keyst1=0.3,t2=0.4,t3=0.5,t4=0.6, the system control parametersa= 35,b= 6,c= 20,k= 6,α= 0.1,β= 0.02 of 4D MHS, the discard valueN0=1000 of the hyperchaotic sequences, and the compression rate CR=0.5.

The test objects of the experimental simulation are five grayscale images of size 512×512“Baboon”,“Cameraman”,“Lake”,“Lena”,and“Peppers”.

4.1.Encryption and decryption results

The proposed encryption scheme is used to test the encryption and decryption of the above five images,and the experimental results are shown in Fig.9.

Fig.9.Different grayscale images to test encryption and decryption effect:(a)–(e)plaintext images,“Baboon”,“Cameraman”,“Lake”,“Lena”,and“Peppers”;(f)–(j)corresponding ciphertext images;(k)–(o)corresponding reconstructed images.

The size of the plaintext imagePand the reconstructed imageDare 512×512,and the size of the ciphertext imageCis 256×512.The ciphertext image is a noise-like image,from which no valid information related to the plaintext image can be obtained, and the quality of the reconstructed image after decryption is good,which indicates that the proposed scheme has good encryption and decryption effects,and the size of the plaintext image is compressed, which is more convenient for image transmission and storage.

4.2.The analysis of reconstructed image quality

In order to quantitatively evaluate the quality of the reconstructed images, peak signal-to-noise ratio(PSNR)and mean structural similarity (MSSIM) are used to evaluate the visual quality of the images.

4.2.1.Peak signal-to-noise ratio (PSNR)

The PSNR is often used to evaluate the quality of the decrypted image,which is calculated according to

whereX(i,j)andY(i,j)indicate the two images to be tested,MandNare the number of rows and columns of the images.

The PSNR values between the reconstructed images and the plaintext images are shown in Table 2.The PSNR values of the five images are between 30.1355 dB and 36.4641 dB with an average value of 34.1084 dB,and the PSNR value of each image is higher than 30 dB,which indicates that the proposed algorithm is effective and the decryption algorithm has a good image reconstruction effect.

Table 2.The PSNR values between the reconstructed images and the plaintext images.

4.2.2.Mean structural similarity (MSSIM)

The MSSIM is a measure of the similarity of two images,the closer the MSSIM value is to 1,the smaller the difference between the two images,the more similar the two images are,and the smaller the image distortion.The MSSIM is calculated according to

whereµxandµyare the mean values ofxandy,respectively.σ2xandσ2yare the variances ofxandy, respectively.σxyis the covariance ofxandy.XiandYiindicate thei-th block of the plaintext imageXand the reconstructed imageY, respectively, andNis the number of blocks.As usual, we set thec1=(k1L)2,c2=(k2L)2,k1=0.01,k2=0.03,L=255.

The MSSIM values between the reconstructed images and the plaintext images are shown in Table 3.The MSSIM values of the five images are between 0.9913 and 0.9974,and the average value is 0.9937.The MSSIM value of each image is above 0.99 and close to 1,which indicates that there is a high similarity between the reconstructed image and the plaintext image,the quality of the reconstructed image is good,and the proposed algorithm has a good image fidelity.

Table 3.The MSSIM values between the reconstructed images and the plaintext images.

4.3.Statistical analysis

4.3.1.Histogram analysis

The histogram reflects the distribution of pixel values in the image.The plaintext image has its own characteristics,and its histogram is not uniformly distributed, and the histogram obtained by the secure image encryption algorithm should be uniform and flat, from which no valid information about the plaintext image can be obtained.

We plotted the histograms of the plaintext image,ciphertext image,and reconstructed image of the above five images in Fig.10, respectively.It can be seen that the histograms of each ciphertext image are uniform and flat, and the histograms of the ciphertext images are similar and flat regardless of which plaintext image is encrypted.The histograms of the reconstructed images and the histograms of the plaintext images have obviously similar characteristics.

4.3.2.Correlation analysis between adjacent pixel

The adjacent pixels of the plaintext image are generally strongly correlated in all directions, and their correlation coefficients are close to 1.However, the adjacent pixels of the ciphertext image obtained by the secure image encryption algorithm should be weakly correlated in all directions,and their correlation coefficients are close to 0.The correlation coefficientρxyis calculated according to

whereNis the number of pixels of the image,xiandyiare the pixel values of the adjacent pixels of the image, andandare the average values of two adjacent pixels.

The correlation coefficients are calculated by randomly selecting 5000 pairs of adjacent pixels from plaintext images and ciphertext images in horizontal,vertical,and diagonal directions.The results are shown in Tables 4 and 5, and the distributions of adjacent pixels in each direction are shown in Figs.11 and 12.

As can be seen in Fig.11,the adjacent pixels of the plaintext image in three directions are concentrated on the diagonal.From Fig.12,it can be seen that the adjacent pixels of the corresponding ciphertext image in the three directions are spread over the whole coordinate space.From Tables 4 and 5,it can be seen that the correlation coefficient of the plaintext image in each direction is close to 1, and the correlation coefficient of its corresponding ciphertext image in each direction is close to 0.This indicates that the proposed algorithm can effectively reduce the strong correlation between the neighboring pixels of the plaintext image and can effectively resist the statistical analysis attack.

Fig.10.Histograms plotting results: (a)–(e)histograms of plaintext images,“Baboon”,“Cameraman”,“Lake”,“Lena”,and“Peppers”;(f)–(j)histograms of ciphertext images;(k)–(o)histograms of reconstructed images.

Fig.12.Adjacent pixels distribution of ciphertext images: (a)–(e) horizontal direction, “Baboon”, “Cameraman”, “Lake”, “Lena”, and “Peppers”; (f)–(j)vertical direction;(k)–(o)diagonal direction.

Table 5.Correlation coefficients of adjacent pixels in three directions of the ciphertext images.

4.3.3.Information entropy analysi

The information entropy of an image can represent the randomness of image information, and can be used to evaluate the randomness of an image before and after encryption.For an 8-bit grayscale image, the ideal value of information entropy is 8,which is calculated according to

wherev(si)indicates the probability of occurrence ofsiandkis the total number of bits ofsi.

The information entropy of the plaintext images, ciphertext images and reconstructed images are tested separately,and the results are shown in Table 6.The information entropy of the five ciphertext images are between 7.9983 and 7.9987,and the average value is 7.99852, and the information entropy of each ciphertext image is above 7.998, which is close to the ideal value 8.This indicates that the ciphertext images have high randomness and the proposed algorithm has better security.

Table 6.The information entropy of different plaintext images,ciphertext images,and reconstructed images.

4.4.Key space analysis

The keys of the proposed algorithm include the 256-bit hash keyK, the external keysti(i=1, 2, 3, 4) and the intermediate keyscA2min,cA2max,cVHD2min,cVHD2max,kr,kc.If the computing accuracy of the computer is 10-14, the key space of the proposed algorithm is about(1014)4×(1014)6=10140>2400≫2100.Therefore,the key space of the proposed algorithm is large enough to effectively resist exhaustive attacks.

4.5.Key sensitivity analysis

The sensitivity of the algorithm to the keys is an important index to evaluate the security of the algorithm, which can be evaluated from two aspects: first,from the encryption point of view,a small change in the encryption keys can lead to a completely different ciphertext image; second, from the decryption point of view, the plaintext image cannot be accurately reconstructed even if there is only a slight difference between the decryption keys and the encryption keys.The number of pixels change rate (NPCR) and the unified average changing intensity(UACI)are calculated according to

wheremandnare the sizes of the image,D1(i,j)indicates the pixel value of the correct ciphertext image at coordinate(i,j),andD2(i,j)indicates the pixel value of the incorrect ciphertext image at coordinate(i,j).

From the encryption point of view, the sensitivity of the algorithm to the encryption key is tested for the above five images.The external keyst1,t2,t3,t4are changed in turn by the amount of∆=10-14and the other three keys are kept unchanged to obtain the corresponding ciphertext images,respectively.The values of NPCR between them and the correct ciphertext image are calculated separately and the results are shown in Table 7.It can be seen that the average value of NPCR between each incorrect ciphertext image and the correct ciphertext image is 99.6090%,which is close to the ideal value of 99.6094%.Therefore,when the encryption key is changed slightly,the correct ciphertext image cannot be obtained.

Table 7.The NPCR values of changing the encryption keys t1,t2,t3,and t4 in turn.

Taking the “Lena” image as an example, we change the encryption keyst1,t2,t3,t4in turn,and the corresponding ciphertext image and its difference with the correct ciphertext image are shown in Fig.13.It can be seen that there is a big difference between the correct ciphertext image and the ciphertext image after the small change of encryption key.

Fig.13.Ciphertext images of the“Lena”image: (a)ciphertext image under correct encryption keys;(b)–(e)ciphertext images after encryption keys t1,t2,t3,t4 are changed in turn;(f)–(i)difference images of panels(b)–(e)and(a).

From the decryption point of view,the algorithm is tested for the sensitivity of the decryption key.The ciphertext images are decrypted using the keys with minor changes respectively,where the keyst1,t2,t3,t4are changed by 10-16,10-16,10-15,10-15.The decryption results are shown in Fig.14.It can be seen that when the decryption key used is changed slightly,the ciphertext image cannot be decrypted correctly,and the plaintext image is reconstructed.Therefore,the proposed algorithm has high sensitivity to the key in both the encryption and decryption stages.

Fig.14.Reconstructed images of the“Lena”image: (a)reconstructed image under correct decryption keys: (b)–(e)reconstructed images after decryption keys t1,t2,t3,t4 are changed in turn.

4.6.Differential attack analysis

The ability to resist differential attacks is an important metric to evaluate the encryption effectiveness of the algorithm,and two numerical metrics,NPCR and UACI,are usually used to evaluate the degree of difference between two images.

Table 8.NPCR values of changing the pixels of different positions.

The pixel values at coordinates (1,1), (256,256), and(512,512) of the above five plaintext images are incremented by 1 to obtain their corresponding ciphertext images.The NPCR values and UACI values between these ciphertext images and the correct ciphertext images are calculated and the results are shown in Tables 8 and 9.It can be seen that the average value of NPCR is 99.6040%, which is close to the ideal value of 99.6094%, and the average value of UACI is 33.4853%,which is close to the ideal value of 33.4635%.This indicates that the proposed algorithm has a high sensitivity to plaintext image changes and can effectively resist differential attacks.

4.7.Robustness analysis

Ciphertext images are vulnerable to noise and data loss attacks during transmission,and the type and intensity of noise and the degree of data loss affect the quality of reconstructed images.The proposed algorithm is tested for noise attacks and clipping attacks to analyze its robustness.

4.7.1.Noise attack analysis

Taking the“Lena”image as an example,we add different levels of Gaussian noise(GN),Speckle noise(SN)and Salt&Pepper noise(SPN)to the ciphertext image to obtain the corresponding ciphertext images.These ciphertext images are decrypted,and the results are shown in Figs.15–17.The PSNR values between the corresponding decrypted images and the plaintext images are calculated, and the results are shown in Table 10.

It can be seen that GN and SN affect the quality of the reconstructed images, while SPN has almost no effect on the quality of the reconstructed images.And the quality of the reconstructed image gradually decreases with the gradual increase of noise intensity.However, the reconstructed images can still be clearly recognized.

The PSNR values of the images are in the interval[14.4746,23.6611]dB,[17.1695,35.6329]dB,and[35.1842,35.6329] dB when the intensity of the three noises increases from 1×10-6to 9×10-6in order.This indicates that the proposed algorithm is robust to the three noise attacks.

Fig.15.Ciphertext images and the corresponding reconstructed images under GN attack: (a)–(e)the ciphertext images under GN intensity in order of the intensity of 1×10-6,3×10-6,5×10-6,7×10-6,9×10-6,(f)–(j)reconstructed images corresponding to panels(a)–(e).

Fig.16.Ciphertext images and the corresponding reconstructed images under SN attack: (a)–(e)the ciphertext images under SN intensity in order of the intensity of 1×10-6,3×10-6,5×10-6,7×10-6,9×10-6,(f)–(j)reconstructed images corresponding to panels(a)–(e).

Fig.17.Ciphertext images and the corresponding reconstructed images under SPN attack: (a)–(e)the ciphertext images under SPN intensity in order of the intensity of 1×10-6,3×10-6,5×10-6,7×10-6,9×10-6,(f)–(j)reconstructed images corresponding to panels(a)–(e).

Table 10.PSNR values under different noise attack intensities.

4.7.2.Cropping attack analysis

In this section, we use the “Lena” image as an example to test the cropping attack on its ciphertext image.The cut sizes are 32×32, 64×64, 128×128, and the corresponding ciphertext images are decrypted, and the results are shown in Fig.18.The PSNR values between the corresponding images are calculated,and the results are shown in Table 11.It can be seen that the quality of the reconstructed image decreases as the cut size increases.Even if 1/4 of the ciphertext image is lost,the reconstructed image can still be recognized by human eyes,which indicates that the proposed algorithm is robust to the cropping attack.

Fig.18.Ciphertext images and the corresponding reconstructed images under cropping attack.

Table 11.PSNR values under different cropping attack intensities.

4.8.Known-plaintext and chosen-plaintext attacks analyses

Known-plaintext attacks and chosen-plaintext attacks are two common attacks in cryptosystems, and this section analyzes the ability of the proposed algorithm to resist these attacks.

On the one hand, the 256-bit hash keyKbased on the plaintext image and the external keystijointly determine the initial valuesx0,y0,z0,w0of the 4D MHS to generate the four hyperchaotic sequencesX,Y,Z,W.These sequences will be used to generate the initial values0and the sequences of system control parametersui,viof the 1D CCS,to scramble the approximation componentcA,to generate the two random phase masksM1 andM2 of the DRPE encryption process,to generate the Latin square matrixL,to participate in the confusion process and the diffusion process.

On the other hand,the row keykrand the column keykcbased on the plaintext image also participate in the confusion process and the diffusion process.Therefore, the whole process of the proposed algorithm is closely related to the plaintext image information,and the algorithm can effectively resist both known-plaintext attacks and chosen-plaintext attacks.

4.9.Performance analysis of the DCMM

In this section,we compare the performance of the deterministic chaotic measurement matrix(DCMM)with the Gaussian matrix,Bernoulli matrix,Toeplitz matrix,part Hadamard matrix,sparse random matrix,and circular matrix.

The seven measurement matrices mentioned above are tested separately, and their results are shown in Fig.19 and Table 12.It can be seen that the DCMM has a similar image reconstruction effect with the remaining six random measurement matrices, which shows the effectiveness of the DCMM constructed in this paper.The average PSNR value of DCMM is 34.1084 dB,which is only 0.397 dB less than the maximum average PSNR value of 34.5054 dB.However,the DCMM can substantially reduce the space consumption of keys in transmission and storage.

Fig.19.PSNR values of the reconstruction results using different measurement matrices.

Table 12.Comparison of PSNR(in unit dB)of reconstructed images with different measurement matrices.

4.10.Comparison with other compressed sensing encryption schemes

In this section,the proposed scheme in this paper is compared and analyzed with the schemes proposed in Refs.[30,52–56]in terms of the performance of the algorithms.In order to provide a relatively fair comparison environment,the comparison data are algorithmic data from the relevant literatures,where the test images are all 512×512 in size,and the comparison results are shown in Table 13.

Table 13.Comparison with other compressed sensing encryption schemes.

It can be seen that compared with the schemes proposed in Refs.[30,52–56],The proposed scheme has a good performance in various tests, such as the quality of reconstructed images is better and the security of the scheme is higher.The average PSNR value of the five test images is 34.1084 dB,which is higher than the average PSNR value of the comparison schemes of 33.3931 dB.The average value of MSSIM is 0.9937, which is close to 1.The average correlation coefficient of adjacent pixels in the ciphertext images is 0.0045,which is lower than the average of 0.0064 in the comparison schemes.In the differential attack test,the average NPCR value is 99.6090%,close to the ideal value of 99.6094%,and the average UACI value is 33.4855%,close to the ideal value of 33.4635%; The average information entropy of ciphertext images is 7.99852, which is close to the average of 7.99857 in the comparison schemes.The key space of the proposed scheme is 10140>2400≫2100,and among all the comparison schemes,the key space is the largest.

4.11.Running time analysis

In this section, the running time of the proposed algorithm is analyzed.Table 14 provides the time required to process different images using this algorithm.It can be observed that the average time required to encrypt a plaintext image of size 512×512 is approximately 2.2028 s, while the average time required to decrypt a ciphertext image of size 256×512 is approximately 8.9843 s.

Taking the“Lena”image as an example,the specific distribution of time required for encryption and decryption is analyzed,as shown in Fig.20.The encryption process mainly includes the stages of keys and sequences generation,DWT,first round of confusion, CS, DRPE encryption, second round of confusion(CMDPHL),and diffusion(DMDPH),which takes a total of 2.1947 s.Among these stages, diffusion consumes the most time,accounting for nearly 40%.The decryption process mainly includes the stages of inverse diffusion, inverse second round of confusion, DRPE decryption, OMP reconstruction, inverse first round of confusion, and inverse DWT,which takes a total of 8.9773 s.Among these stages, OMP reconstruction takes the longest time,exceeding 80%.

Table 14.Encryption and decryption times for different images.

Fig.20.The encryption and decryption time distribution of the“Lena”image.

5.Conclusion

In this paper,an optical image encryption algorithm based on a new 4D MHS and compressed sensing is proposed.Firstly, we designed the 4D MHS and proved that it has a larger key space, richer dynamical behavior, and more complex hyperchaotic properties.The system improves the security proposed of algorithm.Secondly, we proposed a method for constructing deterministic chaotic measurement matrix(DCMM).The control parameter sequences and initial value of the system are determined by four sequences of 4D MHS,and the DCMM is obtained by bringing them into 1D CCS.The DCMM obtained through this method has strong randomness, effectively reducing the transmission and storage space of keys while ensuring the quality of reconstructed images.Thirdly, DRPE encryption used fractional Fourier transform,which increased the key space and improved the security of the algorithm.Fourthly, the confusion method and diffusion method needed the row keykrand column keykcbased on plaintext images.The generation of four sequences and the DCMM are closely related to the hash key of plaintext image,and the whole algorithm is sensitive to plaintext image.The experimental results and performance analysis show that the proposed algorithm has a large key space,high key sensitivity,better image reconstruction quality, good security, and effectiveness,and can resist a variety of attacks.

Although the proposed algorithm has good security, it is not efficient enough in terms of time efficiency.Taking the image with the size of 512×512 as an example, the average encryption time of this algorithm is 2.2028 s,and the average decryption time is 8.9843 s.In the follow-up work,we will try to combine with deep learning to improve the time efficiency of the algorithm on the premise of ensuring sufficient security of the algorithm.