浅谈1C r18 Ni10 T i 不锈钢管材数控弯管技术

文/钟琪平（国营芜湖机械厂）

1Cr18Ni10Ti 不锈钢管材因耐腐蚀、强度高、延伸率高、比强度高的特点，被广泛用于飞机液压系统的管路中。传统1Cr18Ni10Ti 不锈钢管材的弯曲采用手工弯曲方式，小批量的弯制采取此种方式尚能应对，但大批量的弯制成形则需采用数控弯管的方式，以提升效率和形状质量。

数控弯管是一种基于矢量弯管原理的绕弯工艺，数控弯管机通过Y、B、C 三个轴的运动，可弯制出各种形状的导管。因数控弯管过程中，材料发生弹塑性变形，夹紧力卸载后，弯曲的导管会发生“回弹”现象，造成弯制后的导管弯曲角减小，弯曲半径增大。为提升1Cr18Ni10Ti 不锈钢管材的弯曲精度，本研究以1Cr18Ni10Ti 不锈钢管材为载体，通过弯曲不同角度的弯角，检测回弹后的弯曲角度，研究1Cr18Ni10Ti 不锈钢管材的弯曲规律，并开展多种补偿方法实验，探究不同补偿方法对提升1Cr18Ni10Ti 不锈钢管材数控弯管精度的效果。

一、实验过程

1.实验材料

实验选用外径6 毫米、壁厚0.6 毫米，经固溶处理的1Cr18Ni10Ti 不锈钢管材，管材的化学成分见表1。

表1 1Cr18Ni10Ti 不锈钢管材化学成分

其室温下的主要性能见表2。

表2 1Cr18Ni10Ti 不锈钢管材机械性能

2.弯曲实验

如图1 所示，将外径6 毫米、壁厚0.6 毫米，经固溶处理的1Cr18Ni10Ti 不锈钢管材放在BLM SMART型数控弯管机上，设定弯曲半径为24 毫米，在弯管机各项工艺参数不变的情况下，在10°～130°范围内，以10°为阶差，开展13 组数控弯曲实验。

图1 SMART 型数控弯管机

二、实验结果与讨论

1.弯曲角度结果与分析

如图2 所示，实验后使用ROMER INFINITE 2.0 关节臂测量系统检测管材弯曲后的角度。

图2 测量设备及弯曲的导管

1Cr18Ni10Ti 不锈钢管材的弯曲试验结果见表3。

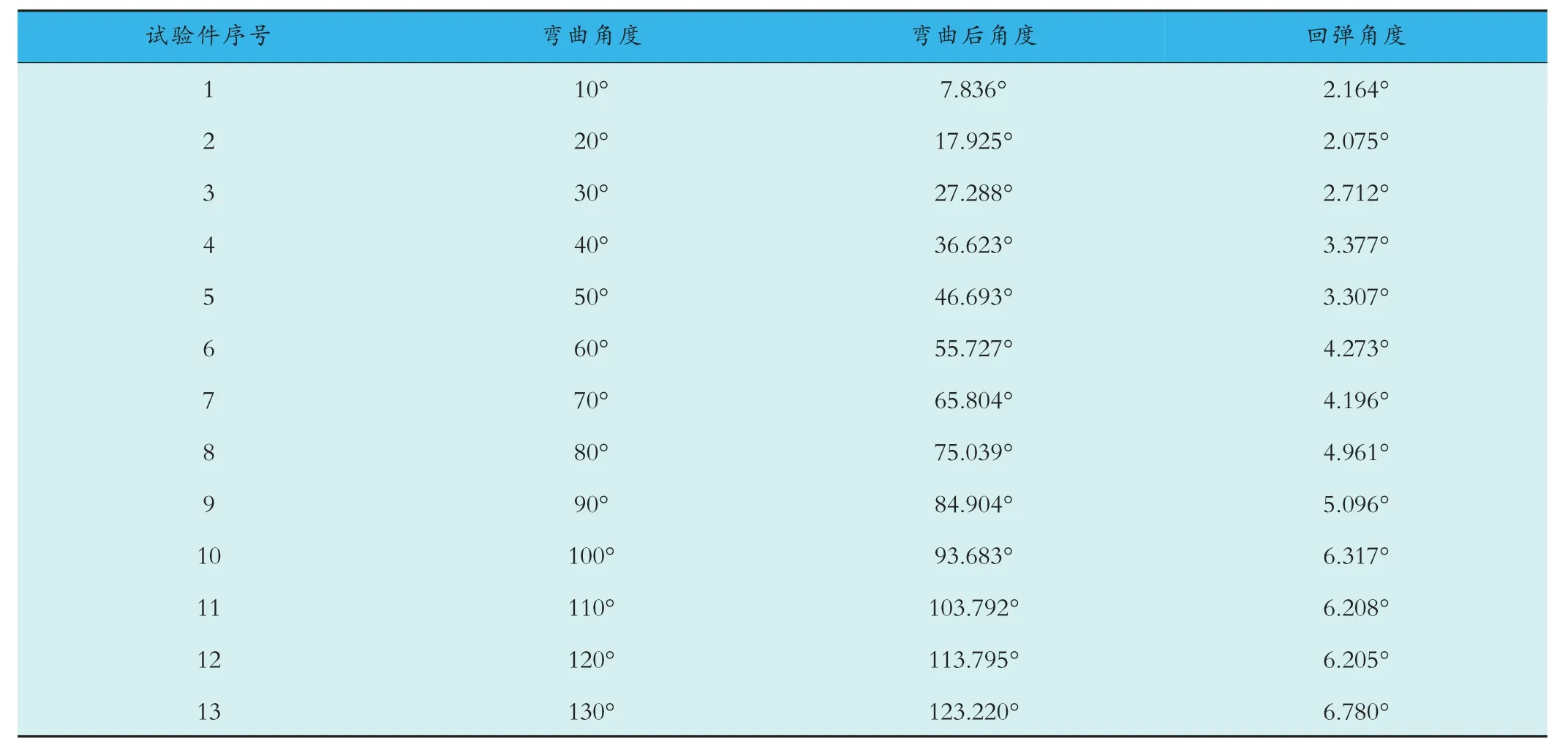
表3 弯曲实验结果

根据表3 数据建立弯曲后角度C2 与弯曲角度C1之间的关系，如图3 所示。

图3 弯曲后角度与弯曲角度之间的关系

线性拟合后，弯曲后角度C2与弯曲角度C1的关系式为：

拟合优度为0.999932，弯曲后角度C2与弯曲角度C1呈线性关系。

根据表3 数据建立回弹角度Δc与弯曲角度C1之间的关系，如图4 所示。

线性拟合后，回弹角度Δc与弯曲角度C1的关系式为

拟合优度为0.966616，回弹角度Δc与弯曲角度C1近似呈线性关系。

通过比较两种拟合方式的拟合优度，弯曲后角度C2与弯曲角度C1呈线性关系，可表达为：

式中：K为比例系数，B为固定系数。

2.回弹补偿分析

根据上述得出的1Cr18Ni10Ti 不锈钢管材弯曲规律，弯曲后角度C2与弯曲角度C1呈线性关系，通过三个角度20°、70°、120°的数控弯曲，使用测量设备测量回弹后的导管弯角，弯角结果见表4，采用三种方法建立回弹规律关系。

表4 20°、70°、120°弯曲结果

两角度线性补偿分析：回弹补偿方法1 是使用20°、120°的弯管数据，根据式（3）建立表达式，表达式为：

三角度线性补偿分析：回弹补偿方法2 是使用20°、70°、120°的弯管数据，根据式（3）建立表达式，表达式为

三角度分段线性补偿分析：回弹补偿方法3 是以20°、70°弯管数据根据式（3）建立第1 段的表达式，以70°、120°弯管数据根据式（3）建立第2 段规律表达式。

补偿结果验证：为验证上述三种方法的优劣，设置弯制一根含44°和94°理论弯角的导管，使用上述三种回弹方法求解需弯曲的角度值，将求解的需弯曲角度值输入BLMSMART 型数控弯管机中，弯曲后测量弯曲后角度，数值见表5。

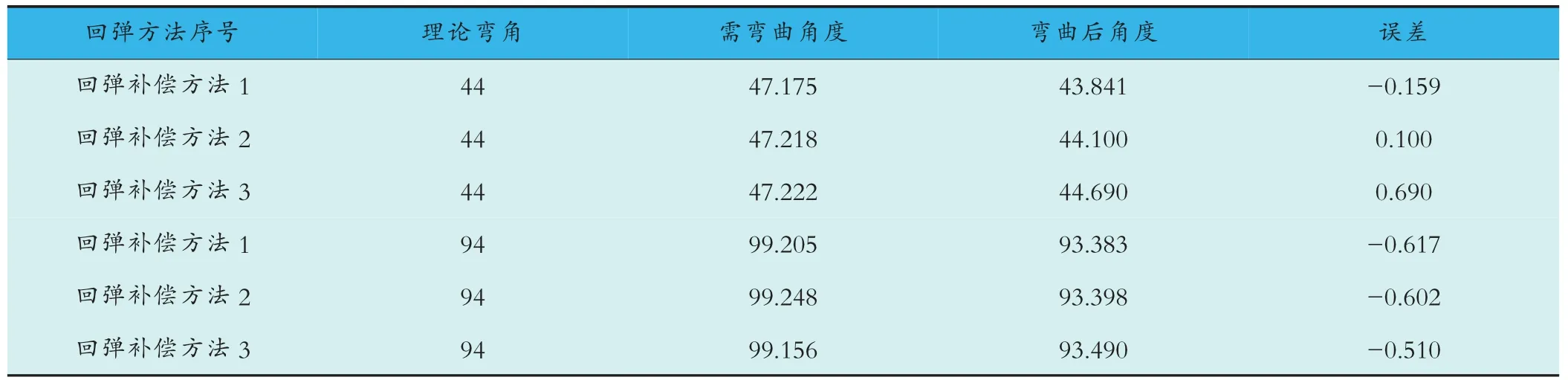
表5 三种回弹补偿方法实验结果

从表5 可以看出，弯曲后的角度误差均小于1°，可满足使用要求。需弯曲角度在三种回弹方法下最大相差小于0.100°，但实际弯曲后角度误差最大相差0.849°，主要原因为管材塑性性能存在差异。

三、结论

对1Cr18Ni10Ti 不锈钢管材进行数控弯管时，弯曲后角度与弯曲角度呈线性关系。两角度线性补偿、三角度线性补偿，三角度分段线性补偿在弯曲数值上差距较小，均能满足使用要求。实际生产中，可使用两角度线性补偿的方法，弯曲试验较为简单。从实验中进一步发现，超高精度弯管需建立在稳定的管材性能上。