压电式振动能量回收方法及实验验证

李 冲, 陈 梁, 方记文, 钟 伟

(江苏科技大学机械工程学院, 江苏镇江 212100)

引言

随着经济社会的发展,人类对于能源的需求不断增加,许多化石资源日益枯竭,能源问题成为全体人类共同面临的一大难题。许多学者注意到在外界环境中存在许多振动能量,尤其是在机械运转过程中,许多能量以振动的形式消耗,将这些振动能量回收利用能够减少能量损耗、提高能量利用效率[1-4]。目前,对于振动能量的回收主要有4种形式: 静电式[5]、 电磁式[6-7]、压电式[8]、 摩擦电式[9]。 电磁式基于电磁感应定律,利用振动使得感应线圈磁通量变化,从而实现能量转化[10];压电式基于压电效益,利用晶体内部的极化将振动能量转化电能[11];静电式基于可变电容收集振动能量[12];摩擦式通过静电感应完成振动能量转化[13]。其中压电能量回收装置具有使用能量回收效率高、结构简单、不发热、寿命长、功率密度高等优点,被广泛应用于机械振动的能量回收之中[14]。压电能量回收装置常采用线性压电振子结构,这种结构在接近共振频率时能量回收效率高,但是当其偏离共振频率时能量收集效率显著降低,使得能量回收装置的效率低。因此,研究扩大线性压电振子结构的频率带宽十分有前景。

近期学者发现旋转式压电能量收集器具有上变频机制,能够将低频转动转换为高频振动,起到拓宽频带的作用[15]。许多研究人员因旋转式压电能量收集器的上变频拓宽频带的机制,投入对其的研究当中。WANG J X等[16]提出了一种基于梯形梁的旋转压电能量回收装置,验证了旋转压电能量回收装置具有上变频等优点以及梯形悬臂梁相比矩形悬臂梁能够承受更高的应力。TAN Q等[17]设计了一种低频旋转的宽带能量回收装置,利用离心式软化梁阵列回收装置实现低频旋转下的高能量输出。SHI G等[18]研究了一种由旋转球驱动的磁性耦合多向超低频波压电振动能量回收装置,该压电能量回收装置可以从单方向或多方向的激励中俘获能量,当外部频率为0.9 Hz,外部负载为47 kΩ 时,整个能量采集器的功率输出为6.32 mW,显示出巨大的应用前景。

因此,本研究设计了一种用于回收机械振动的筒形凸轮压电能量回收系统,并通过实验验证其性能。该装置通过压电悬臂梁末端磁铁与凸轮磁铁的磁耦合作用,利用上变频机制拓宽压电悬臂梁工作带宽。首先介绍振动能量回收系统的设计思路以及其基本结构,并且对振动能量收集系统工作过程进行分析。接着分析其能量回收的机理以及建立其理论模型,通过ANSYS仿真分析系统的频率响应。最后利用NI数据采集卡和LabVIEW软件搭建实验测试平台,对压电能量回收装置的性能进行实验测试。

1 结构及工作原理

如图1a所示,筒型凸轮压电能量回收装置由悬臂梁、压电片、磁铁、支撑架、滑块、筒型凸轮组成。悬臂梁一端固定在支撑架上,自由端附着一磁铁,固定端处粘合压电片。筒型凸轮旋转压电能量回收装置通过滑块往复运动,带动筒型凸轮旋转。筒型凸轮一面粘合磁铁,随着凸轮旋转,凸轮上的磁铁逐渐靠近悬臂梁磁铁,产生磁力;接着凸轮继续旋转,磁力逐渐消失,悬臂梁因此振动,压电片随悬臂梁振动变形发电。图1b是当筒型凸轮旋转时,凸轮磁铁与悬臂梁磁铁磁耦合示意图。

图1 系统结构图Fig.1 Structure diagram of system

图2为图1b的等效示意图,当筒型凸轮上的磁铁运动到B位置时,与悬臂梁上磁铁开始耦合,此时压电悬臂梁由于磁力作用开始产生形变。筒型凸轮上的磁铁运动到A位置时,磁铁间的作用力达到最大值。当筒型凸轮上的磁铁运动到C位置时,与悬臂梁上磁铁结束耦合。由于磁力的变化,压电悬臂梁不断振动。

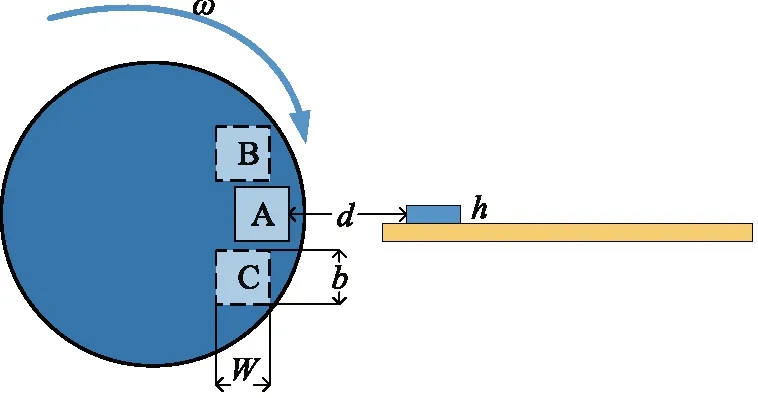
图2 压电能量回收系统的工作过程Fig.2 Working process of piezoelectric energy harvesting system

当筒型凸轮旋转时,凸轮上的磁铁与悬臂梁上磁铁的磁力F(t)呈现周期性变化。磁力变化周期T0=60/nm,其中n为筒型凸轮的旋转速度,m为筒型凸轮上的磁铁个数。磁耦合时间Tr=60l/πnR,其中R为筒型凸轮的半径,l为磁铁在筒型凸轮上的弧长。磁力作用对于压电能量回收极其重要,令FM为磁力F(t) 的幅值,磁力可以进行下列描述:

(1)

磁力F(t)与一般正弦激励不同,对磁力F(t)通过傅里叶变换展开为正弦和余弦形式,其中式(2)中ω表示筒型凸轮上的磁铁旋转频率,表示悬臂梁振动的固有频率。

(2)

其中,基频ω=2Tπ=30πnn0,a0,aj,bj是常系数,可知:

(3)

(4)

(5)

根据式(2)可知,在磁激励下悬臂梁的振动有多个峰值,这些峰值所对应的频率呈现上变频的特点。

2 理论模型构建与仿真分析

2.1 理论模型构建

图3为压电能量回收装置的动力学模型。图中M为等效质量,C为等效阻尼,K为等效刚度。能量回收装置由于受到磁力F影响,产生了X(t)的相对位移。图4为系统的电学模型。根据机电等效原理,将等效动力学模型转化为等效电学模型,其中质量块等效为电感,阻尼转化为电阻,弹簧转化为电容,电磁元件转化为回转器,电压元件转化为变压器。其中E为压电部分产生的电压,Cp为压电部分的等效夹持电容,R为负载电阻,α为压电力压转换因子。其中能量回收装置所受到的惯性力可以表示为:

(6)

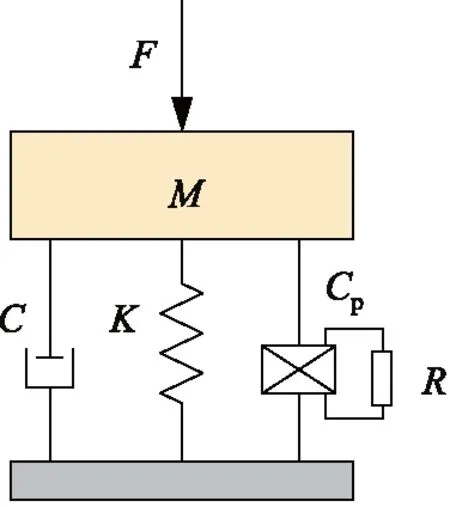
图3 系统动力学模型Fig.3 Dynamic model of system

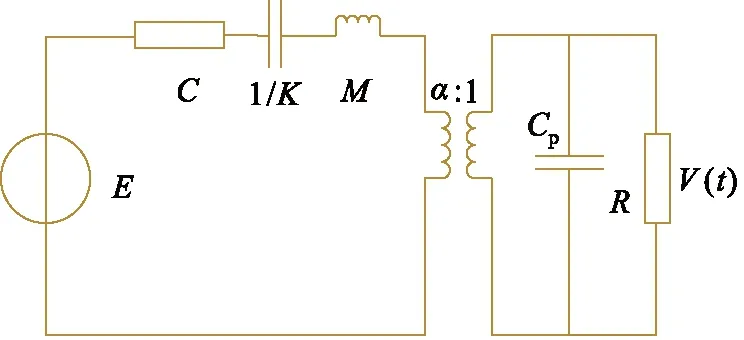
图4 系统电学模型Fig.4 Electrical model of system

其中,压电发电导致的反作用力Fp所损耗的能量就是压电部分所收集到的能量,有:

Fp=aV(t)

(7)

结合式(6)与式(7),可以建立压电振动能量回收装置的运动微分方程,即:

(8)

根据图4系统的电学模型结合基尔霍夫电流定律,可以得到:

(9)

对式(9)进行拉普拉斯变化,经过推导可以求得:

(10)

在只考虑纯电阻负载R的条件下,用频率的均方根来对压电能量回收装置的性能进行评估。u为压电悬臂梁末端相对位移,根据式(9)和式(10)可以推导出压电振动能量回收装置的功率,即:

(11)

2.2 仿真分析

在完成系统动力学模型与电学模型的构建分析后,对简化的压电能量回收系统进行ANSYS仿真,并且对仿真结果进行分析。如图5所示,为压电能量回收系统简化模型的前三阶模态分析,其固有频率分别为24.265, 151.96, 317.59 Hz。ANSYS仿真的目的是为了得到压电悬臂梁的固有频率,进而通过得到的固有频率来设计实验中压电能量回收装置的参数与变量,以此来优化其发电性能。

图5 ANSYS仿真图Fig.5 ANSYS simulation diagram

从仿真结果可以看出,筒形凸轮压电能量回收系统在一阶模态响应下工作性能最稳定,压电元件不易损毁。为了获得最优发电性能,激励频率应该尽可能接近压电元件的固有频率。压电元件的固有频率为24.265 Hz,筒形凸轮旋转1圈激励压电元件4次,所以凸轮转速为6.0 r/s时发电性能最优,即360 r/min。

3 实验分析

通过搭建一个实验平台如图6所示,来测试筒形凸轮压电回收系统的性能。通过电机往复运动模拟液压机械振动,通过凸轮及磁耦合传递能量,振动频率为主要影响因素。此外,通过Arduino和驱动器来控制电机速率以此来改变激励的频率,利用可调电阻器作为负载来测试压电回收系统的输出特性。使用NI USB-6002数据采集(DAQ)卡和LabVIEW软件来获取实验数据进行分析。

图6 实验平台Fig.6 Experimental platform

本研究重点是设计一种用于回收液压系统或电机往复冲击能量的筒形凸轮压电能量回收系统,并且设计方案和实验平台来验证可行性。因此本研究不涉及能量管理电路设计,而是侧重于对压电能量回收系统的输出电压测验分析及功率计算。

对能量回收系统施加瞬间激励进行测试,测试结果如图7所示,代表在相同频率不同阻抗下系统输出电压。图8显示了瞬间激励输出电压和功率随负载的变化。

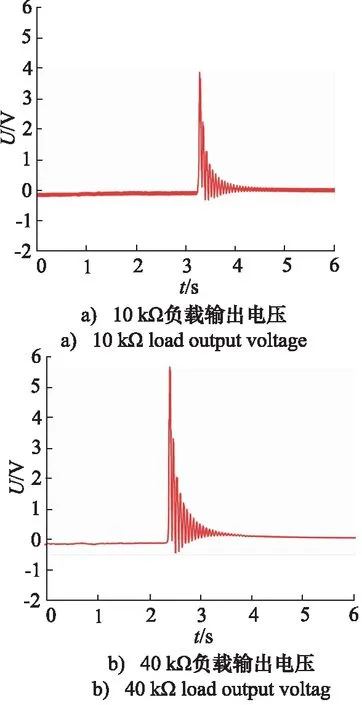
图7 瞬间激励输出电压波形图Fig.7 Waveform diagram of instantaneous excitation output voltage

图8 瞬间激励下电压及功率随电阻变化图Fig.8 Diagram of voltage and power variation with resistance under instantaneous excitation

从图8可以看出:

(1) 在瞬间激励下,能量回收系统产生瞬间电压,系统在不同负载下瞬间电压峰值不同;

(2) 随系统负载电阻值增加, 能量回收系统输出电压变大;

(3) 系统的功率变化在瞬时励磁下比较稳定。负载为10 kΩ时取得最大功率为1.44 mW。

所提出的压电能量回收系统在连续励磁发电机的输出特性进行了研究。如图9所示,为能量回收系统在连续激励不同负载下的输出电压。

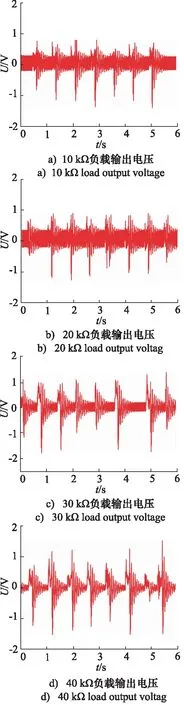
图9 连续激励下输出电压随电阻变化图Fig.9 Diagram of output voltage variation with resistance under continuous excitation

图9中可以看出在连续激励下,压电能量回收系统的输出电压随负载电阻增加而增大,且输出电压比较稳定,但同样也能知道随着负载电阻的增大,电压增加的幅度较小,因此还需要探究功率与电阻之间的关系。最后探究压电能量回收系统的输出电压以及功率与激励频率之间的关系,如图10所示为负载20 kΩ时,在不同频率下的输出电压。图11为负载20 kΩ时,在不同频率下的功率。

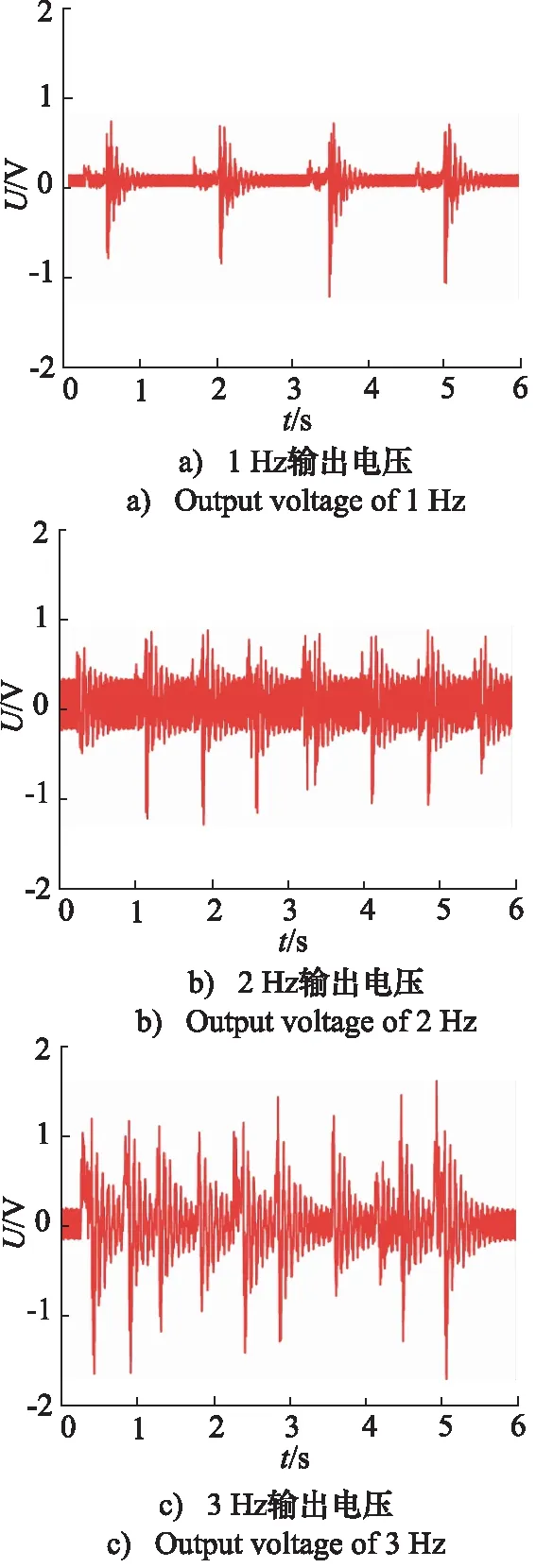
图10 输出电压随频率变化图Fig.10 Diagram of output voltage with frequency

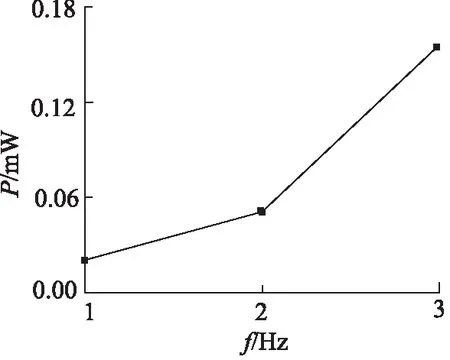
图11 功率随频率变化图Fig.11 Diagram of power as a function of frequency

从图10中可以看出,当负载电阻恒定时振动频率越高时,压电能量回收系统的输出电压越高。并且输出电压的波峰数也随频率增大而增多。从图11中可以看出,当负载电阻恒定时振动频率越高,压电能量回收系统所产生的功率越高,且到3 Hz时达到最大功率0.156 mW。

通过以上实验数据可以看出,瞬间激励下的输出电压是瞬间的,而连续励磁下的输出电压是随时间连续变化。不同负载下,能量损失也不同,得到的功率也不同,频率越接近悬臂梁固有频率,能量利用效率越高。为了提高压电能量回收系统的性能,可以采取2个措施: 选择合适的负载电阻;利用机械结构控制激励频率,使能量回收系统在合适频率下工作。

在实际应用中,可以通过设置多组能量回收装置,对设备产生的振动能量进行回收。本装置回收能量可以驱动低功率传感器用于监测设备工作振动或测量设备工作温度。

4 结论

本研究提出来一种用于回收机械振动的筒形凸轮压电能量回收系统,给出压电能量回收系统的设计过程。并且对该系统进行动力学分析、机电耦合分析以及ANSYS仿真。利用LabVIEW软件及NI数据采集卡,建立实验平台。实验表明,在瞬间激励下最大输出功率可以有1.44 mW。在连续激励下,压电能量回收系统的输出电压和功率跟系统负载电阻大小及激励频率相关,且当负载为20 kΩ时在3 hz下的功率为0.156 mW。回收能量可用于监测机器工作状态,研究成果促进了压电能量回收系统的应用与推广。