RSM优化冲焊型液力变矩器叶片冲压工艺及回弹抑制

陈勃含, 刘 城,2, 闫清东,3, 魏 巍,4

(1.北京理工大学机械与车辆学院, 北京 100081; 2.北京理工大学车辆传动重点实验室, 北京 100081; 3.北京理工大学前沿技术研究院, 济南 250300; 4.北京理工大学重庆创新中心, 重庆 401135)

引言

液力变矩器是一种以液体为工作介质传递能量的复合液力传动元件,以其优良的自适应性能、增矩变速、过载保护性能等特性被广泛应用于各类车辆中[1-2]。液力变矩器根据制造方式分为铸造型和冲焊型,其中冲焊型液力变矩器的泵轮、涡轮叶片采用薄板冲压而成,然而叶片冲压后由于残余应力会产生回弹,使得叶片形状与设计形状存在偏差,导致实际性能无法达到设计需求[3]。

回弹的产生与诸多因素相关,包括材料力学性能、冲压方向、模具形状、冲压工艺参数等,选择合理的冲压工艺参数对提高冲压件质量、减小回弹十分重要。近年来,国内外学者对优化工艺参数做了较多研究,陈吉清等[4]对汽车翼子板的冲压成形基于正交试验方法对工艺参数进行优化设计与分析;田永生等[5]借助Autoform-Sigma模块对汽车A柱内板针对拐角区域开裂、起皱问题对工艺参数进行研究,通过优化拉延筋系数、板料尺寸、摩擦系数和压边力找到无开裂、无起皱的最优参数组合;LI H等[6]提出回弹补偿与工艺参数优化相结合,采用BP神经网络结合遗传算法对铝合金汽车覆盖件的成形厚度进行了优化;CAO Angang等[7]系统研究了弯曲速度、相对圆角半径、温度和对准时间对不锈钢的回弹影响,并得出了适合冲压工艺参数范围。

目前对冲压工艺参数优化研究大多集中于各种钣金覆盖件,对于冲焊型液力变矩器叶片冲压参数优化研究较少。本研究采用Dynaform对某型号冲焊型变矩器涡轮叶片冲压回弹进行有限元仿真计算,采用优化拉丁超立方试验方法,针对减薄率与回弹量构建关于冲压工艺参数的多元回归响应面模型,基于此模型对3种遗传算法对比分析,选择适合的多目标优化算法进行优化求解,得到关于目标函数的Pareto解集,从中选取优化工艺参数组合,并对其进行仿真验证。

1 有限元仿真计算

1.1 有限元仿真模型

根据涡轮冲压模具提取上下模型面作为冲压仿真的凹模和凸模,采用三维软件UG的成形模块对中位面进行展开得到板料,如图1所示;以IGES数据接口输入至Dynaform仿真软件,其中板料厚度T为1.4 mm,材料为DD11;有限元仿真认为冲压模具在成形过程中没有变形,网格大小为1 mm,板料作为变形体进行网格划分,选用壳单元,大小为0.6 mm;划分网格时应多为形状均匀的正方形单元,在模型边缘使用三角形单元以适应形状,要求网格划分不能有相互重叠及崩溃的单元[8]。划分网格后的涡轮叶片有限元仿真模型如图2所示。

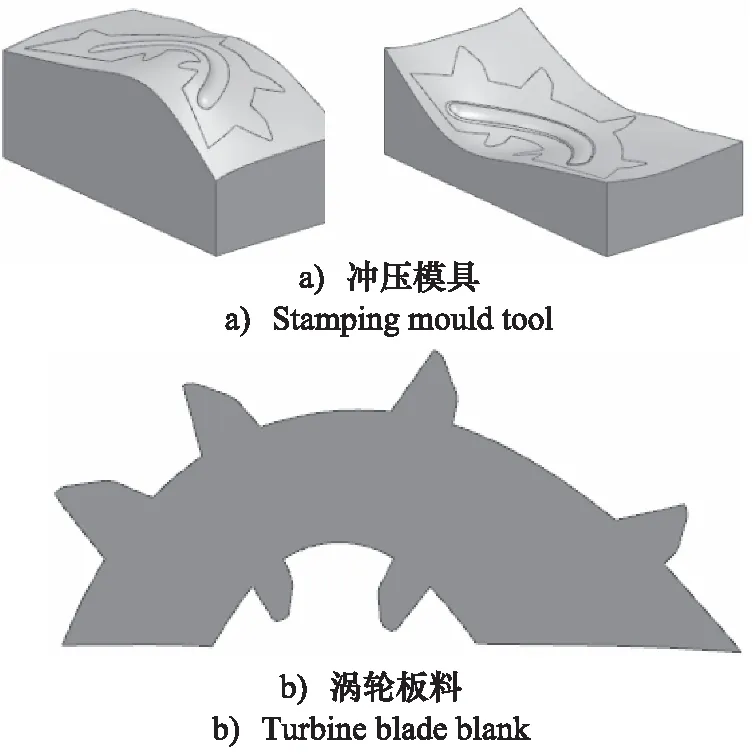
图1 冲压模具及反求板料Fig.1 Stamping mould tool and reverse sheet

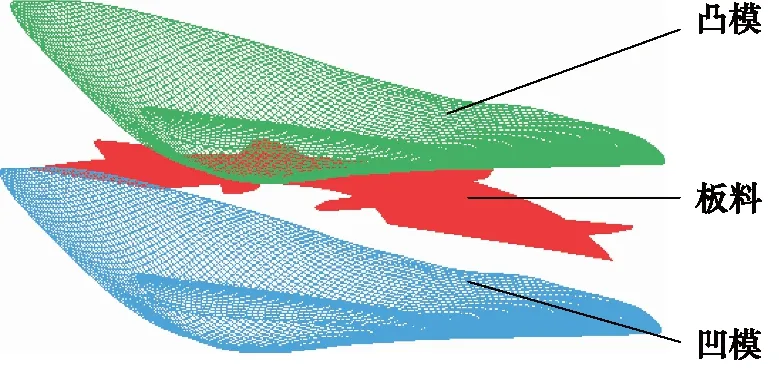
图2 叶片冲压成形模型Fig.2 Blade model of stamping forming

1.2 仿真算法选择

1) 有限元算法选择

有限元法模拟板料冲压回弹的算法有2种,即动力显示算法和静力隐式算法,其中动力显示算法利用中心差分法对时间进行积分[9-10],计算过程不需要列出具体的刚度矩阵,可节省大量计算时间,稳定性好,适用于复杂板料成形计算;静力隐式算法虽然求解时间长,但在计算回弹位移时效率高,可以在少量的迭代步数内得到很好的结果,节省时间[11]。综合2种算法的特性,动力显示算法用来模拟冲压成形过程,采用无压边形式的单动成形工艺;静力隐式算法模拟回弹。

2) 回弹模拟方法选择

回弹模拟分为有模法和无模法[12]。有模法模拟精度高,但耗时长。无模法将各单元的等效节点力反向作用在板料上计算,所有节点等效力接近于零时卸载结束,无需进行接触判断,计算时间少[13],故本研究使用无模法模拟板料回弹。

1.3 有限元模型验证

采用上述模型设置对涡轮叶片进行冲压成形仿真计算,通过成形极限图判断成形质量,其反映了板料在单向和双向拉应力作用下抵抗颈缩或破裂的能力,当单元位于拉裂趋势临界线以上即存在发生拉裂的趋势,如图3所示。零件拉裂质量评价公式如下[14]:

(1)

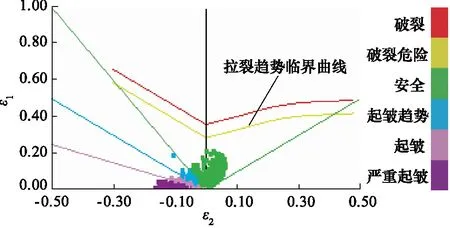
图3 成形极限图Fig.3 Forming limit diagram

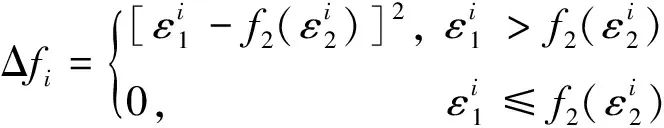
(2)

式中,N—— 选取的单元数

f2(x) —— 成型极限图上的拉裂趋势临界曲线

ε1,ε2—— 主应变、次应变

由式(1)、式(2)可知,当对应单元的主次应变超过拉裂趋势临界曲线时,该单元发生开裂的可能性越大;由成型极限图可知,所有单元应变均位于拉裂趋势临界曲线下方,成形质量满足要求。将得到成形结果进行回弹计算,结果如图3、图4所示,最大回弹位于涡轮入口处,为0.466 mm。

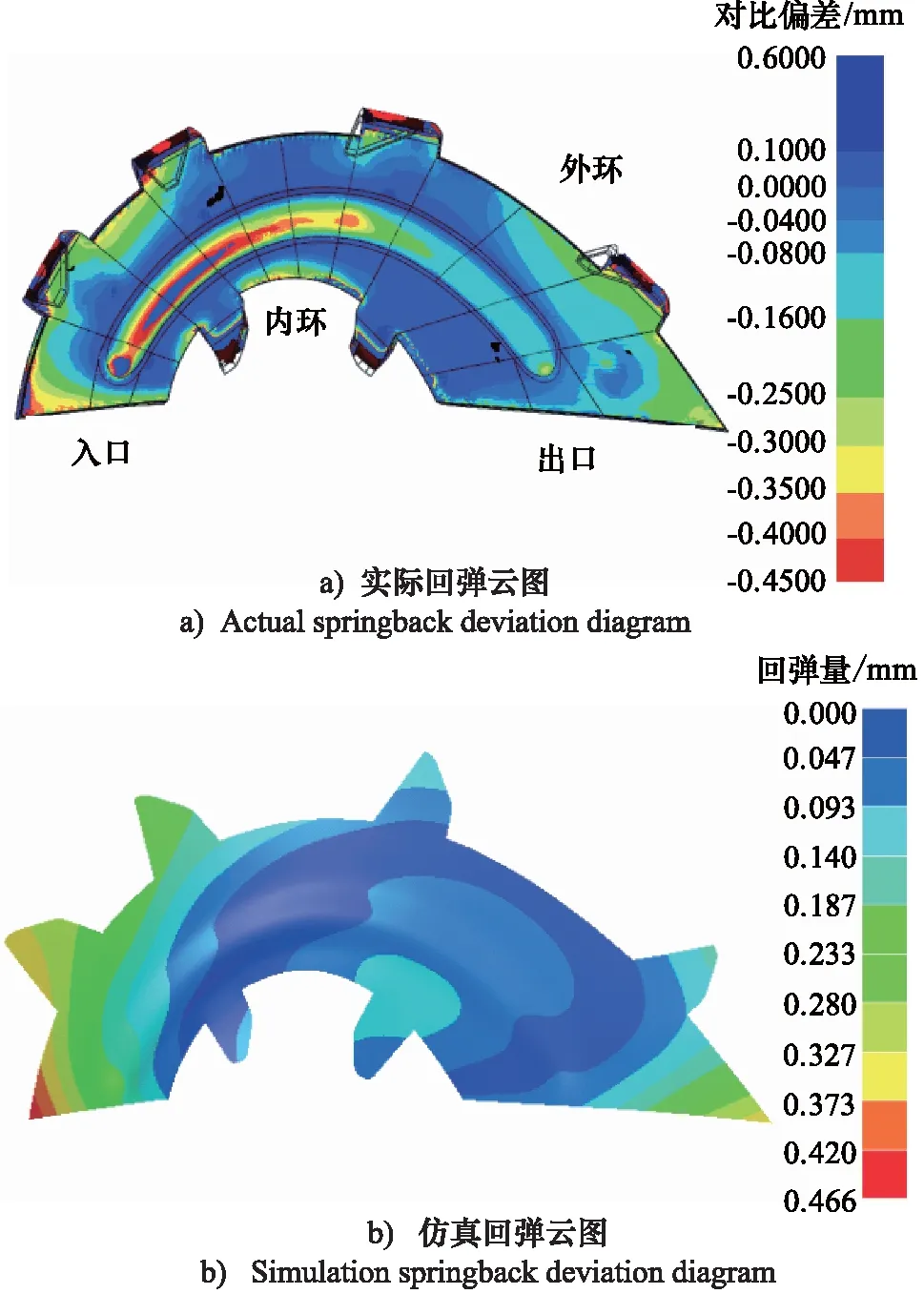
图4 实际与仿真回弹对比Fig.4 Comparison of actual and simulation springback

采用相关设置参数制造叶片样件,扫描处理获得其实际回弹分布;以仿真回弹约束点为基准将扫描样件模型与设计模型对齐,如图4所示,由于拉延筋结构较复杂,小部分区域有突出,其对齐结果显示该区域成形不充分,部分出现正偏差,此与拉延筋设计参数相关,故本研究暂不考虑拉延筋处的成形误差;对于叶片其余区域要求对齐后两者偏差分布均匀、无突变,且对齐区域内最大误差为0.08 mm,远小于最大回弹量,认为可以准确反映实际回弹情况;由对比图得到实际回弹与仿真结果的整体回弹分布相同,最大回弹均出现在叶片入口处,数值模拟误差小于6%,验证仿真模型相关设置均合理可靠,模拟结果可以反映实际回弹。

2 试验设计及分析

2.1 试验设计

试验以某型号冲焊型液力变矩器涡轮叶片为基础,选取模具间隙、摩擦系数和冲压速度作为自变量,以最大减薄率和最大回弹量作为因变量,通过试算确定参数设计范围,避免成形件出现开裂及起皱现象,具体试验设计如表1所示,试验结果如表2所示。

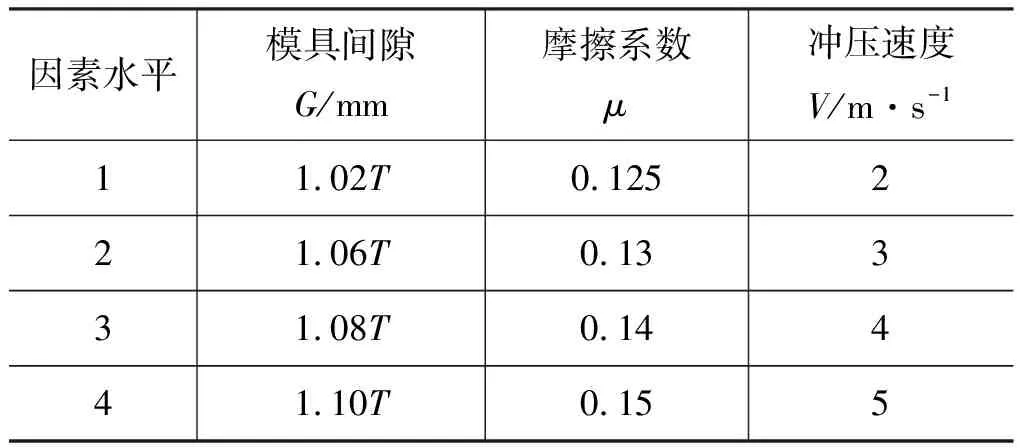
表1 试验因素水平范围Tab.1 Test factor level range

表2 优化拉丁超立方试验结果Tab.2 Results of optimal Latin hypercube test

2.2 敏感性分析

对样本数据分析获得各因素对响应的影响程度,一般用Pareto图表征,包括各因素的线性相关、平方相关及因素之间的交互响应影响程度,如图5所示,横坐标用各相关因素的百分数R判断对响应的影响程度,纵坐标表示各影响因素,其中G代表模具间隙,M代表摩擦系数,V为冲压速度。由图5可以看出,冲压速度对最大减薄率影响最大,但是其余参数的线性相关程度和各因素之间的交互响应影响程度也有明显的影响,不能忽略;模具间隙和冲压速度对最大回弹量影响最大,并且模具间隙的平方相关也有较大影响。

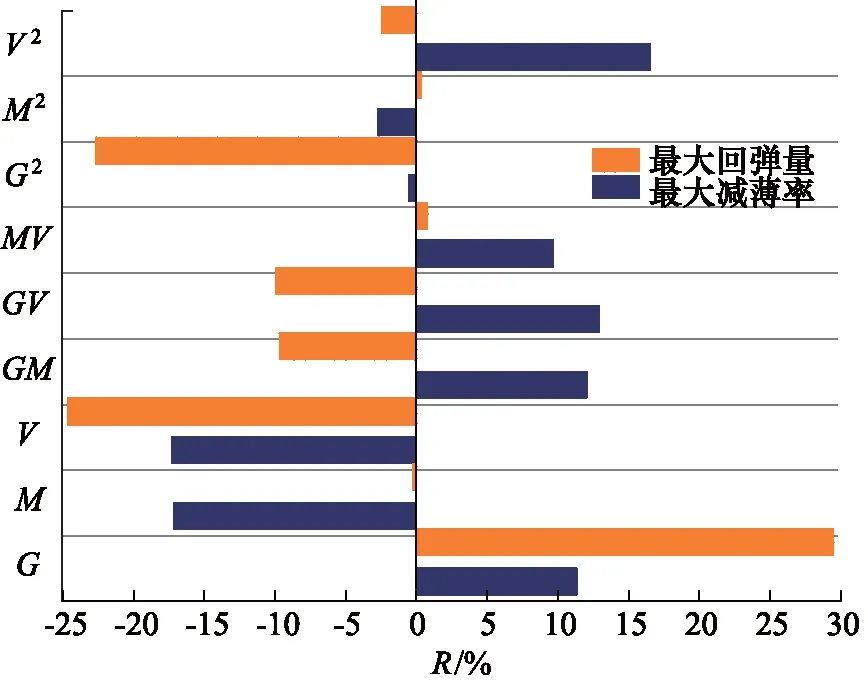
图5 各响应Pareto图Fig.5 Pareto plots for responses

对各因素关于响应的主效应进行分析,如图6所示;模具间隙和摩擦系数对最大减薄率成线性相关,分别为负相关和正相关,冲压速度成二次相关,在速度较小时,最大减薄率随着速度增大而单调增大,当速度大于3.3 m/s后, 最大减薄率随着速度增大呈现减小趋势。摩擦系数对回弹的影响不显著,无明显变化;模具间隙和冲压速度对回弹影响显著,在模具间隙较小时,随着间隙增大,最大回弹量逐渐增大,当间隙大于1.08T后,回弹量随着间隙的增大有小幅减小的趋势;回弹量与冲压速度呈现负线性相关,这与Pareto图分析结果相同。

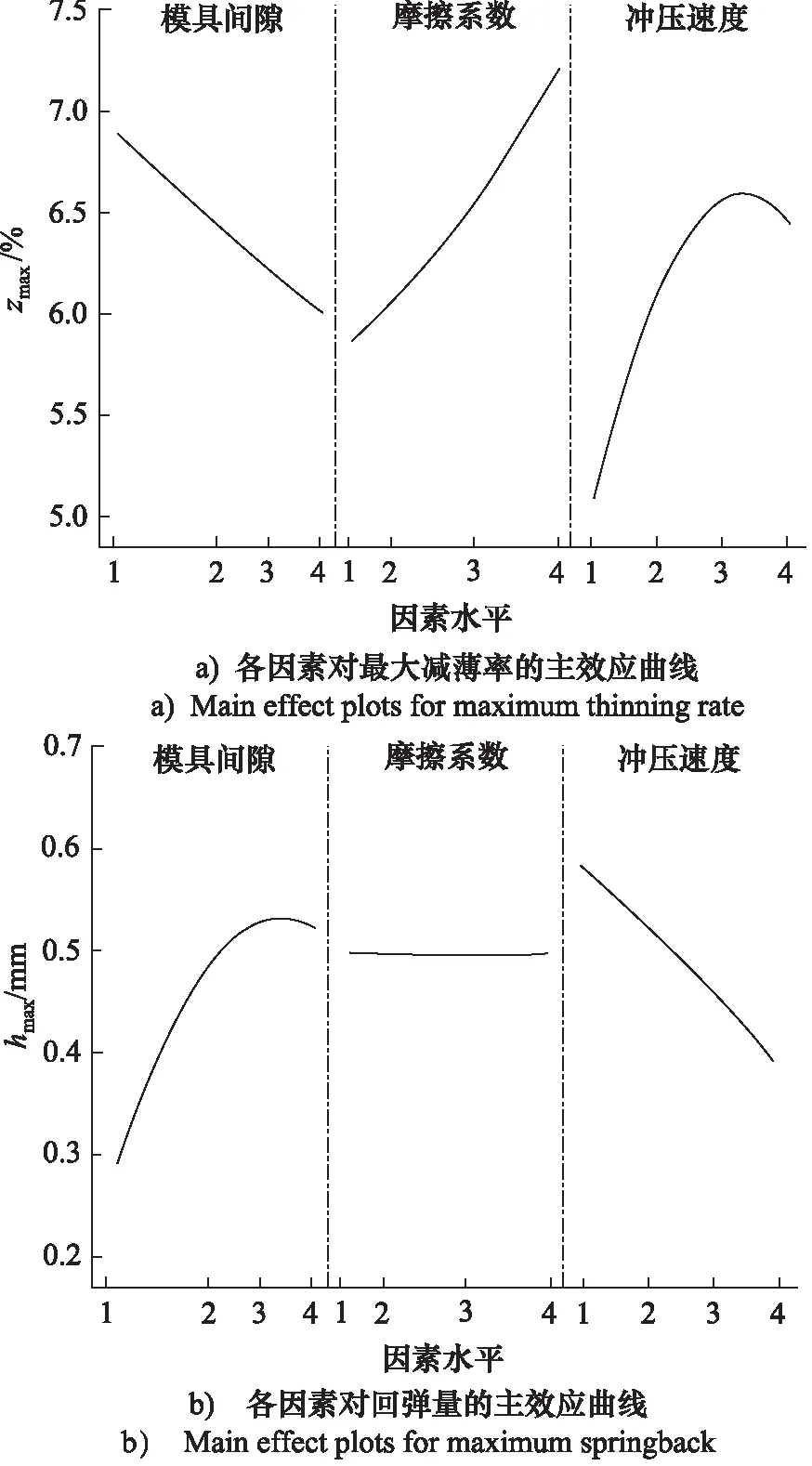
图6 各响应主效应图Fig.6 Main effect plots for responses

3 基于响应面的工艺参数优化

3.1 响应面模型建立

响应曲面法多用来解决多维设计空间优化设计。通过合理的试验设计及计算获得样本数据,利用多元回归方程拟合出自变量与响应之间的曲面函数,并在构造的响应面上优化计算,并将优化结果进行仿真验证后,得到关于响应的优化解[15]。

基于更好的拟合效果及更高的计算精度,忽略三阶及以上的交互响应,采用统计软件Design-Expert对表2仿真结果进行回归分析,构造三元三次响应曲面,其构造方程为:

(3)

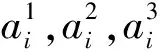
表3 回归方程系数Tab.3 Parameters of regressive equation

表4 响应曲面拟合误差分析Tab.4 Analysis of RSM fitting error

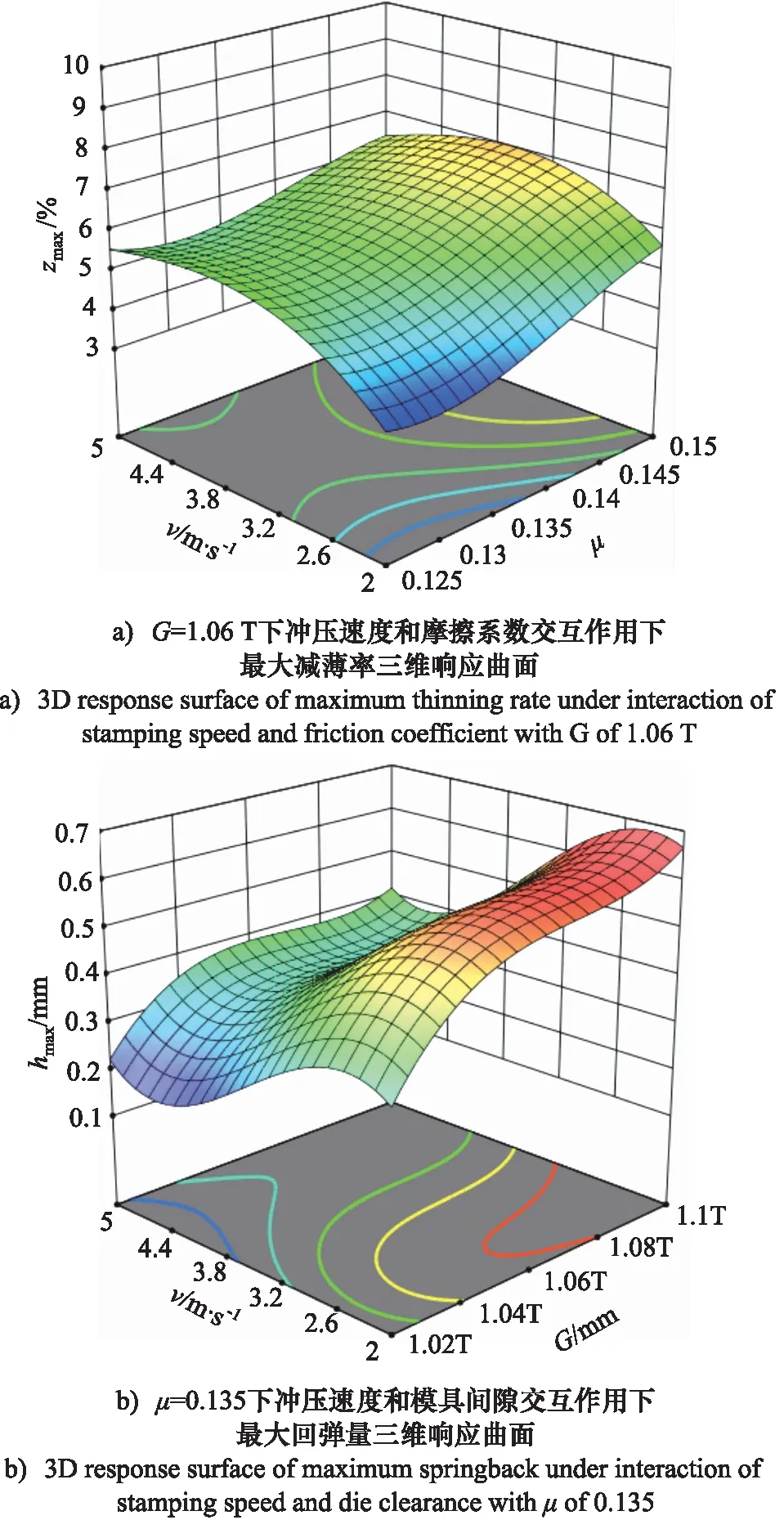
图7 三维响应曲面Fig.7 3D response surface

3.2 优化算法选择

多目标优化是同时对多个目标进行寻优求解,通常各目标难以同时达到最优,此时优化结果不是一个最优解,而是一个优化解集, 对此引入Pareto概念, 多个最优解构成一个Pareto解集,也称为Pareto前沿,设计者根据优化需求选取优化解作为最优。

常用的多目标遗传算法有3种:AMGA、NCGA和NSGA-II,其均是以MOGA(Multi-Objective Genetic Algorithm)算法为基础,是一种具有自组织、自适应、自学习和“复杂无关性”特征的启发式算法。分别采用3种优化算法在拟合响应面上进行多目标优化,各算法参数设置如表5所示,所有算法均进行240次计算,对各算法的搜索能力及解的质量进行对比,为了更有效的搜寻优化解,对响应建立约束条件:

(4)

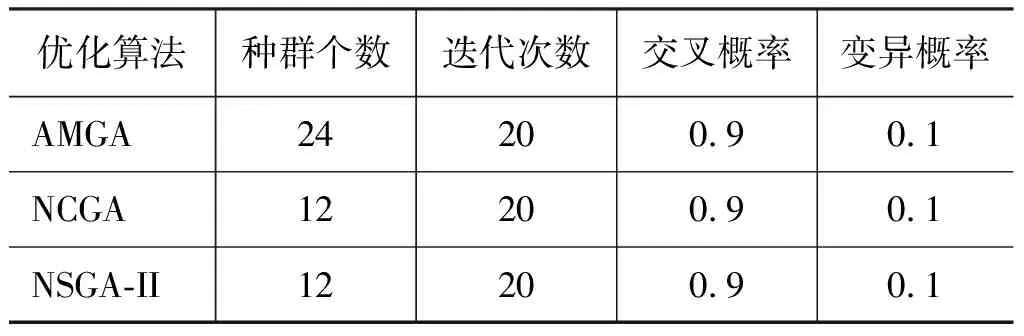
表5 各优化算法参数设置Tab.5 Parameters of optimization algorithms

图8为各优化算法的Pareto前沿,表6为各优化算法计算结果,其中NCGA算法搜索能力较弱,AMGA和NSGA-II算法搜索能力较好,一个满足约束的有效解所需评价次数均小于1.5,而NSGA-II算法搜索Pareto解的效率更高(一个Pareto解需要4.211次评价),并且较AMGA算法,其Pareto解连续性和均匀性较好,主要是因为NSGA-II算法导入了“拥挤距离”和“拥挤距离排序”方法,所以Pareto前沿不会局限于一部分领域里。综合各算法能力,选择NSGA-II优化算法。

表6 AMGA/NCGA/NSGA-II三种算法计算结果对比Tab.6 Comparison of calculation results of AMGA/NCGA/NSGA-II algorithms

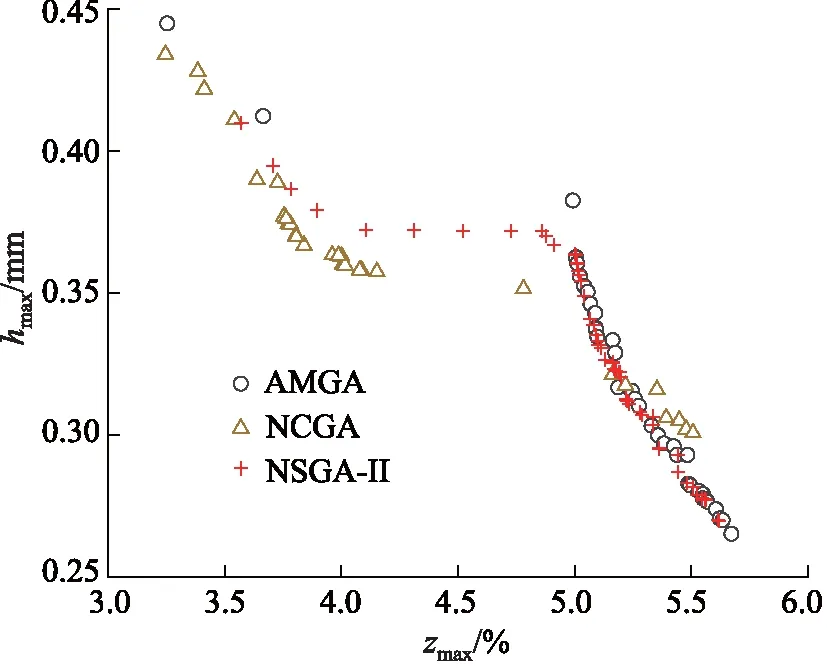
图8 各优化算法Pareto前沿Fig.8 Pareto frontier of optimization algorithms

3.3 工艺参数优化

设定优化算法种群规模为40,其他参数与表5一致,基于响应面求解得到Pareto前沿,如图9所示。通过Pareto前沿可知,整体趋势是随着最大回弹量增大,随最大减薄率降低;在回弹量小于0.35 mm的区域i和回弹量大于0.37 mm的区域iii内,减薄率随着回弹量增大急剧下降,而回弹量在0.35 mm～0.37 mm的区域ii内,减薄率变化缓慢;由于两者之间相互约束,故在区域ii中选择合理参数A保证减薄率和回弹量同时得到优化(如表7所示), 确定工艺参数数值为:模具间隙为1.02T,摩擦系数为0.13,冲压速度为2 m/s。

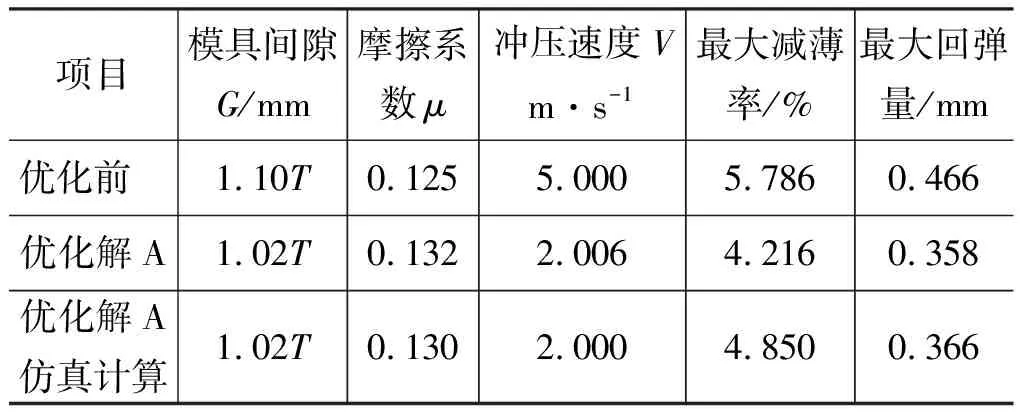
表7 优化前后减薄率及回弹对比Tab.7 Collection of optimum process parameters

图9 NSGA-II多目标优化Pareto前沿Fig.9 Pareto frontier of NSGA-II multi-objective optimization

3.4 仿真验证

采用有限元仿真软件Dynaform对优化工艺参数进行仿真验证,成形后叶片没有破裂产生,其厚度和减薄率分布如图10所示,叶片最小厚度位于拉延筋的入口端,1.322 mm,最大减薄率为4.85%,与预测结果误差0.634%;回弹计算结果如图11所示,最大回弹量0.366 mm,略高于预测结果0.008 mm,仿真结果与响应面优化结果误差在3%以内,说明拟合响应面预测精度较高,满足要求,且NSGA-II算法具有良好的全局寻优能力。优化后的参数较初始参数降低了模具间隙和冲压速度,提高了摩擦系数,从而同时降低了最大减薄率和最大回弹量。

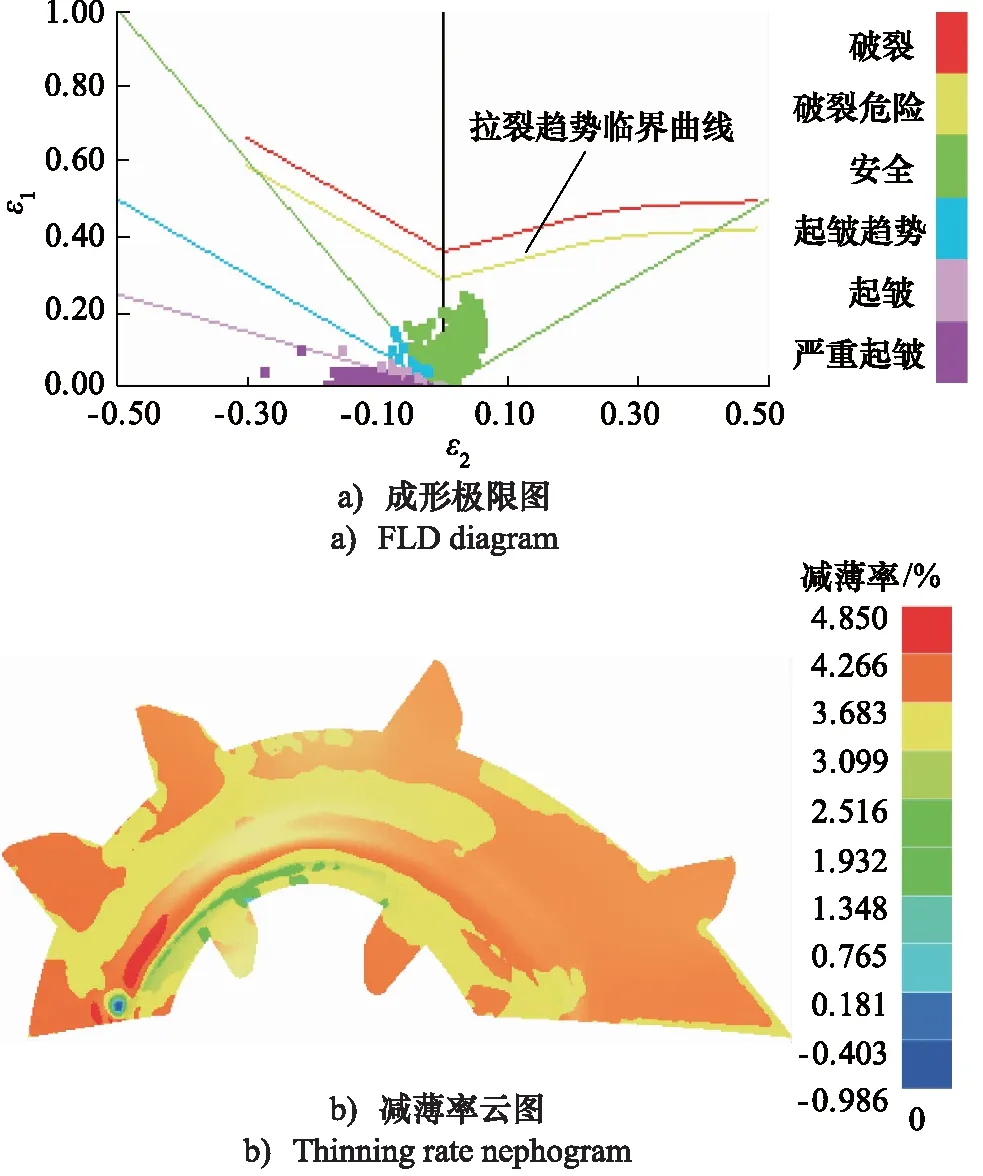
图10 优化后冲压成形结果Fig.10 Optimized forming Results

4 结论

对于冲焊型液力变矩器涡轮叶片成型质量和回弹的多目标优化,基于Dynaform仿真软件,构建有限元计算模型,并制造样件验证模型可靠性;结合响应面法和优化拉丁超立方试验设计方法,分析了各参数对减薄率和回弹的影响规律,并采用NSGA-II多目标优化算法对工艺参数进行了优化设计。

(1) 采用Dynaform有限元软件模拟计算回弹,对比样件实际回弹与仿真结果,其整体回弹分布相同,最大回弹误差小于6 %,仿真结果可以较好的反映实际回弹情况,验证了有限元模型的准确性和可靠性;

(2) 模具间隙和冲压速度对最大回弹量有显著影响,其中模具间隙与回弹量之间为二次相关,冲压速度与回弹量现负线性相关,且模具间隙的平方项对其也有较大影响;摩擦系数和冲压速度对最大减薄率影响最大,其中摩擦系数与减薄率呈正线性相关,冲压速度表征为正二次相关,并且模具间隙和各因素之间的交互效应对其也有明显影响;

(3) 对3种不同多目标遗传算法进行对比分析,对其搜索能力和Pareto解质量进行比较,对此冲焊型液力变矩器叶片工艺参数优化来说,在所评价的算法中,NSGA-II算法求解效率较高,Pareto前沿连续性和均匀性最优;

(4) 基于响应面采用NSGA-II多目标优化算法对工艺参数进行了优化设计,选择合理工艺参数为:模具间隙为1.02 T,摩擦系数为0.13,冲压速度为2 m/s,并进行仿真验证。结果表明拟合响应面具有较高精度,所选NSGA-II优化算法全局寻优能力较强,验证了其预测结果的可靠性。优化后响应较初始均有明显改善,其中回弹减小0.1 mm,减薄率降低0.936%。