Diversity of wave structures to the conformable fractional dynamical model
U.Younas,J.Ren
State Key Laboratory of Power Grid Environmental Protection/Henan Academy of Big Data, Zhengzhou University, Zhengzhou 450 0 01, China
Keywords:Integrability Soliton solutions 3D-WBBM equation Kudryashov and modified Kudryashov method NEDAM
ABSTRACT This manuscript examines the recently developed conformable three-dimensional Wazwaz–Benjamin–Bona–Mahony (3D-WBBM) equation’s dynamical behavior in terms of its spatial and temporal variables.The governing equation is stretch for the Korteweg-de-Vries equation that represents the unidirectional propagation of small amplitude long waves on the surface of hydro magnetic and acoustic waves in a channel,especially for shallow water.Solitary wave solutions of various types,such as kink and shock,as well as singleton,combined solitons,and complex solitons,are all retrieved.Additionally,solutions to hyperbolic,exponential,and trigonometric functions are obtained through the use of recently developed methods,namely the Kudryashov method (KM),the modified Kudryashov method (MKM),and the new extended direct algebraic method (NEDAM).The study conducts a comparison of our findings to wellknown findings,and concludes that the solutions reached here are novel.Additionally,the earned results are sketched in different shapes to demonstrate their dynamics as a function of parameter selection.We can assert from the obtained results that the applied techniques are simple,vibrant,and quite well,and will be helpful tool for addressing more highly nonlinear issues in various of fields,especially in ocean and coastal engineering.Furthermore,our findings are first step toward understanding the structure and physical behavior of complicated structures.We anticipate that our results will be highly valuable in better understanding the waves that occur in the ocean.We feel that this work is timely and will be of interest to a wide spectrum of experts working on ocean engineering models.
1.Introduction
Since the beginning of the universe,scientists have attempted to interpret a variety of phenomena in a variety of scientific fields.However,it took many years for this interpretation to become well established and promising,owing to the complexity of these occurrences,their causes,and consequences,before they could be used for the benefit of human beings.Nonlinear science is one of the most fascinating fields of research in this cutting-edge era of science.As a result of their primary commitment to investigating the true nature of frameworks,researchers have concentrated on obtaining analytically or precisely accurate results.In the vast field of mathematics,the discovery of NLPDEs was one of the more remarkable achievements that helped dispel the darkness that had hampered man’s comprehension.Various physical phenomena are modeled by NLPDEs,and their solutions in the forms of exact and approximate are both significant.For several years,mathematicians and academic groups have found that studying the exact solutions to NLPDEs has been an enthralling and challenging field of study because they are widely used in the study of nonlinear physical phenomena in mathematics and applied physics,with significant applications in a variety of natural science and engineering disciplines,including fluid mechanics,chemistry,thermodynamics,physics,electromagnetism,bio-mathematics,and mathematical physics.Due to their critical contribution to the analysis of nonlinear problems’ real-world aspects,scholars have prioritised finding exact solutions.Due to its widespread use and applications in nonlinear sciences,interest in studying NLPDEs has increased significantly [1–18].Multiple sturdy algorithmic methodologies,such that ()-expansion method [19],anstaz approach [20],the trial equation technique [21],extended sinh-Gordon equation expansion method [22],the adomian decomposition method [23],the variation iteration method (VIM) [24],the modified exp (-φ(ξ))-expansion method [25],the direct algebraic method [26],the extended Fan sub-equation method [27],theF-expansion technique[28],the generalized exponential rational function method [29],newφ6-model expansion method [30] and several others [31–54] have been proposed to examine the nature of various solutions found in the literature for nonlinear physical models,with the goal of fathoming the entire dynamical procedure used to model complicated NLPDEs.

Fig.1. Graphs of solution (33) with parameters α=0.79, Ξ2=-1, Ξ1=2, Ξ4=-3, P=4, R=1, t=1, y=2..
Moreover,ocean engineering is the application of engineering,planning,and management to the state-of-the-art in the science of oceanography.Oceanography is defined as a science dealing with the oceans,including the delimitation of their area and depth,the physics and chemistry of their waters,marine biology,and the exploitation of their resources.That is,ocean engineering can be defined as the practical use of science and mathematics to make the physical and chemical qualities of ocean water and the ocean’s energy sources beneficial to humanity.The shallowwater equations are a collection of hyperbolic partial differential equations that explain fluid flow beneath a pressure surface.Water wave dispersion refers to frequency dispersion in fluid dynamics,which means waves of different wavelengths travel at varying phase speeds.In this context,water waves are waves that propagate on the water’s surface,with gravity and surface tension acting as restoring forces.As a result,water with a free surface is commonly thought of as a dispersive medium.Ocean engineering involves the development,design,operation,and maintenance of watercraft propulsion and ocean systems using a variety of engineering sciences such as mechanical engineering,electrical engineering,electronic engineering,and computer science.Power and propulsion plants,machinery,piping,automation and control systems for all types of marine vehicles,as well as coastal and offshore constructions,are all included [55].Water wave equations describe various nonlinear physical phenomena in the above mentioned areas.
All of our findings are crucial for understanding nonlinear phenomena in dispersive waves,which are important in the field of ocean engineering.Investigating the interaction solutions to the studied model in nonlinear dispersive waves will allow other researchers to conduct additional research on the effects of dispersive waves on coastal processes and waves’ interactions with complex structures in the near shore areas.Mathematical modeling of tsunamis and tidal oscillations can be used as an example to apply this studied equation in oceanic engineering.These types of equations can also be applied in engineering,such as diffraction,refractive prediction,flatness,and prediction of harmonic interactions around coastal structures.
Fractional differential equations,on the other hand,are differential equations that have fractional order derivatives.In Soliton’s theory,there are numerous fractional nonlinear problems.As a result,research is now concentrated on fractional calculus and the development of novel operators such as the Atangana Baleanu derivatives,the Caputo and Riemann Liouville derivatives.Applied sciences and engineering rely on fractional order models because they better reflect real-world conditions.The conformable fractional operator [56,57] remove some of the restrictions associated with existing fractional operators while maintaining traditional calculus properties such as the derivative of the quotient of two functions,the chain rule,the product of two functions,the mean value theorem,and Rolle’s theorem.Using conformable derivatives is easy to understand and implement.Additionally,it aids in our comprehension of the behavior of physical phenomena.The conformable fractional derivative is a powerful tool for resolving complex problems.This derivative was discovered to be more aesthetically pleasing and fantastic than the previous ones implemented.

Fig.2. Graphs of solution (49) with parameters α=0.94, Ξ1=1, Ξ2=2, Ξ3=-1, t=4, y=3, A=e..
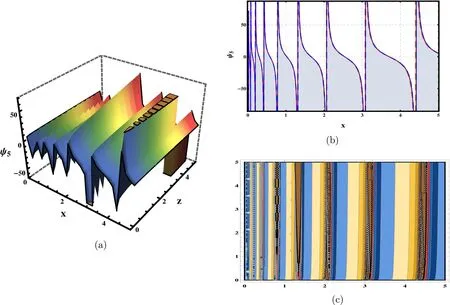
Fig.4. Graphs of solution (55) with parameters α=0.29, δ=2, Ξ1=3, Ξ2=0.1, Ξ4=2, σ=2, t=1, χ=0.2, y=3, D=e..
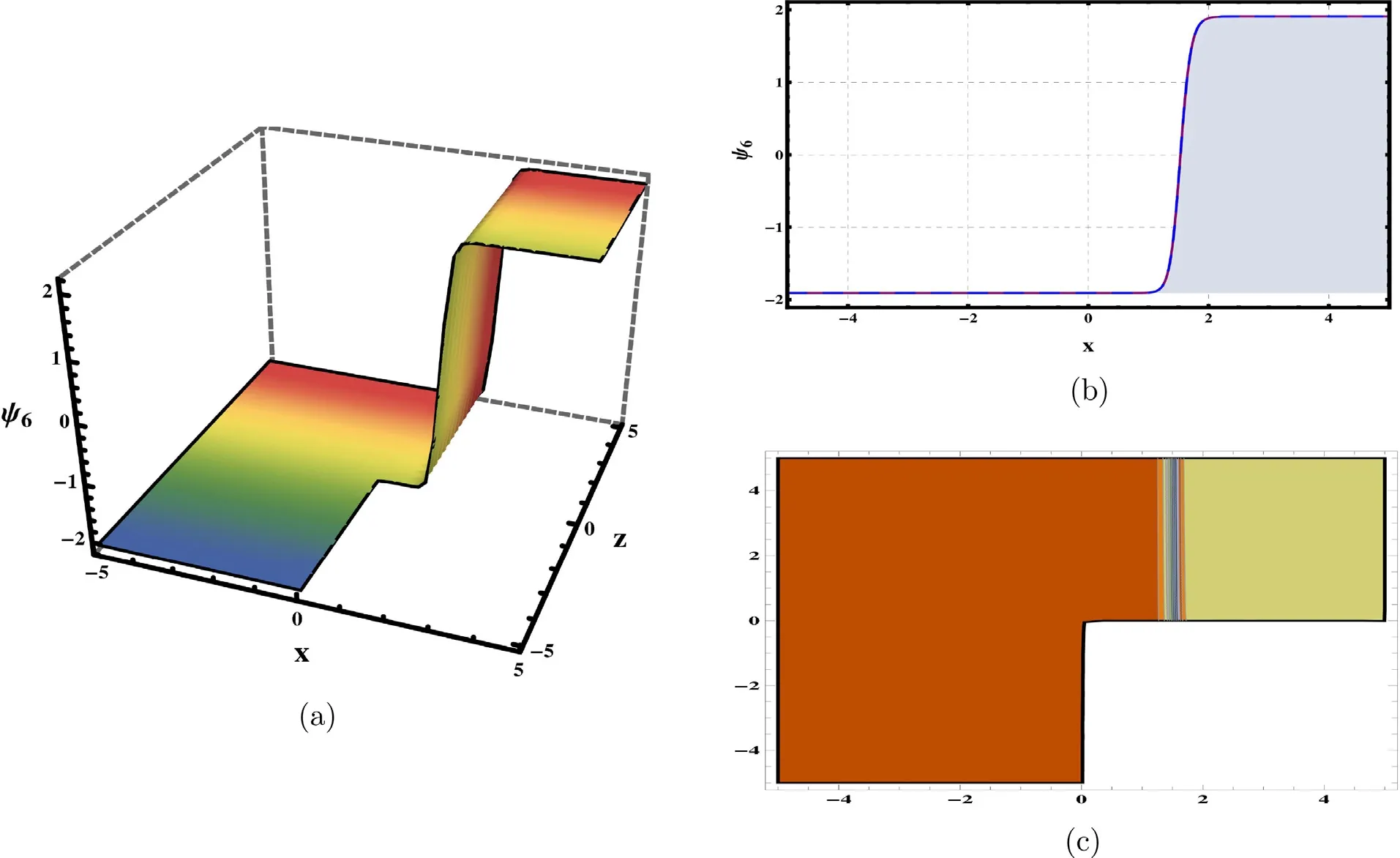
Fig.5. Graphs of solution (56) with parameters α=0.50,δ=1,Ξ1=3,Ξ2=-2,Ξ4=2,σ=0.6,t=0.2,χ=5,y=2,D=e..
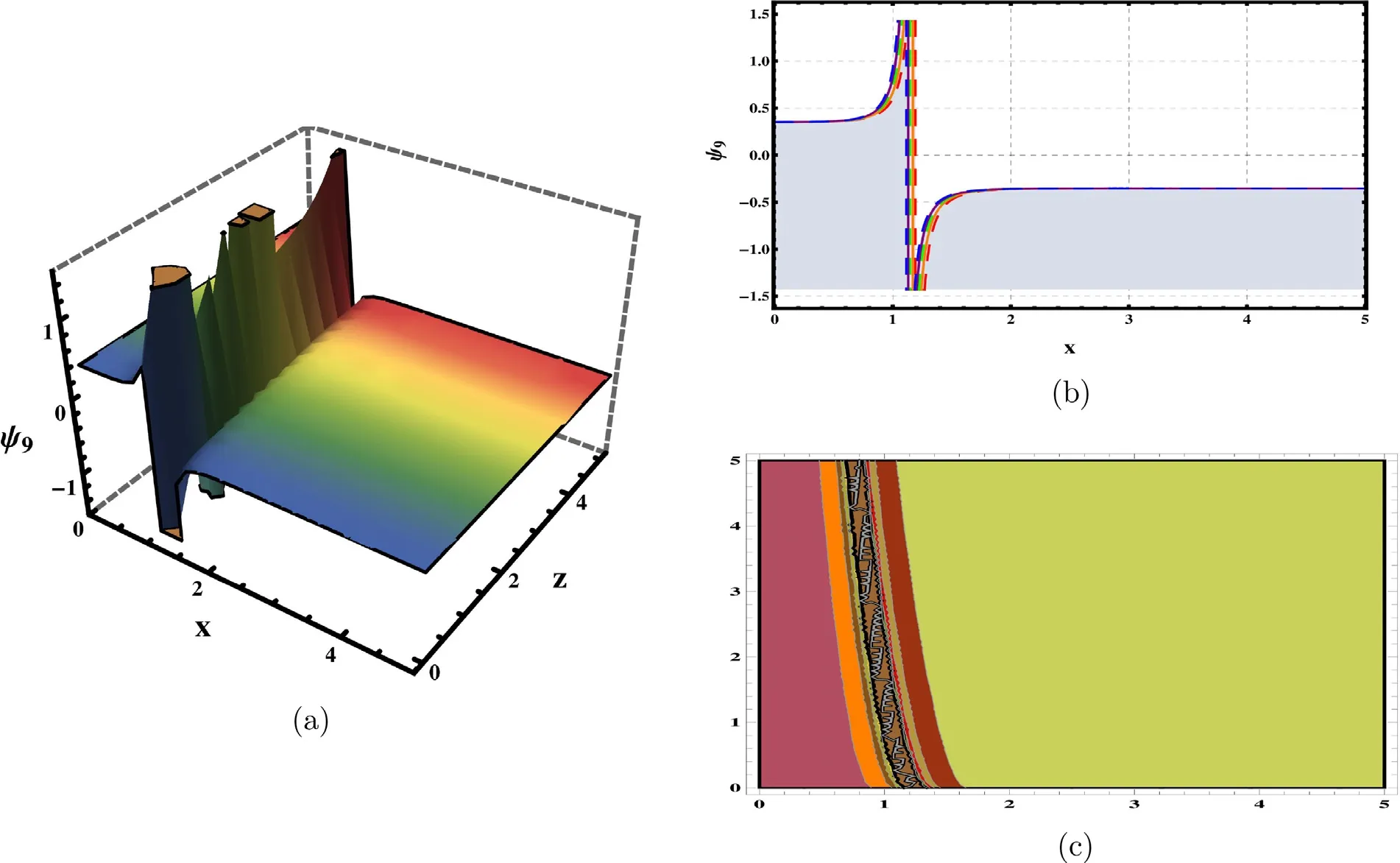
Fig.7. Graphs of solution (59) with parameters α=0.59,δ=0.2,f=0.2,g=2,Ξ1=3,Ξ2=-1,Ξ4=1,σ=0.01,t=2,χ=2,y=3,D=e..
However,in this article,we are interested to apply three developed techniques,called Kudryashov method (KM) [58],modified Kudryashov method (MKM) [59] and new extended direct algebraic method (NEDAM) [60] for finding the different types of solutions to the governing model with conformable fractional derivative system.
This manuscript is arranged as: Methods details in Section 2.Governing model is presented in Section 3,and the properties of conformable derivative in Section 4.The extraction of solutions in Section 5.Concluding remarks are presented in Section 6.

Fig.8. Graphs of solution (79) with parameters α=0.95, δ=5, Ξ1=3, Ξ2=-2, Ξ4=1, σ=-5, t=1, χ=0, y=3, D=e.

Fig.9. Graphs of solution (81) with parameters α=0.35, δ=5, g=8, Ξ1=3, Ξ2=-3, Ξ4=2, σ=0, t=2, χ=2, y=0.6.
2.The governing equation
The BBM model [61,62] is written as follows:
and KdV equation is:
Both Eqs.(1) and (2) are used to study the following types of waves: in water for surface waves,in harmonic crystals for acoustic waves,in compressible liquids for acoustic gravitational waves,in plasma for hydromagnetic waves,and in nonlinear dispersive systems for long waves.See the reference for further information[63–66].
Wazwaz investigated a modified 3D-BBM model in 2017,developing a new model known as the WBBM
Seadawy et al.[72] is refereed as conformable 3D-WBBM model that will used in this work:
The field of ocean engineering is a section of other marine technology that focuses on maritime engineering and marine electronic technology.It is a discipline of technology studies that is concerned with the design and operation of ocean systems and other marine bodies,whereas oceanography is concerned with the natural characteristics of oceans and their dynamics that haven’t the artificial effect.The 3D-WBBM a model that represents the unidirectional propagation of long waves with small amplitude on the hydromagnetic and acoustic waves’ surface in shallow water channel is the new model that is widely used in coastal and ocean engineering as well as models that contain the tsunami waves and other complex structures in which the nonlinearities and dispersion terms are taken in consideration.The considered governing model is concerned with the phenomenon of water waves,which is related to wave energy converters and hence oceanography.A lot of researcher talked about nonlinear phenomena and how they can be used in more ways.This is a very important part of the study of analytical and exact solutions to NLPDEs,and it’s becoming more and more popular [67–71].Now,in the next sections,we analyze the Eq.(6).
3.Conformable derivative
This section discusses the fundamental concepts underlying conformable derivatives.Additionally,it facilitates us to try and make sense of how physical events behave.
Definition :Letg: (0,∞)-→Rbe a function.Conformable derivative has the following definition fort >0 and 0< α≤1.
Supposeα∈(0,1] andgandhareα-conformable differentiable for allt >0.Then :
4.Analysis of the methods
Suppose that a FNLPDE with four independent variablesx,y,z,tas follow:
Whereq=q(x,y,z,t) is an unknown function.In order to solve the Eq.(7),we define the following wave transformation
On arranging the Eqs.(8) and (7),we get NLODE as:
4.1.Description of KM [58]
•Suppose that the Eq.(9) has solution of formQ(ξ)as
whereAi(i=0,1,2,3,·,N)are constants to be determined.Q(ξ) has the following form
wherePandRare the arbitrary constants to be determined.Eq.(11) satisfying following nonlinear ODE
Further,Eq.(12) has the general solution
•TheNvalue can be determined using Eq.(9).As a result,the homogeneous balancing principle is advantageous for equating the nonlinear terms in Eq.(9) with their higher derivatives.Eq.(10) can be expressed as forN=1.
•By combining Eq.(10) with Eq.(9),and then equating the coefficients ofQ(xi)ito zero,we have a cluster of nonlinear algebraic equations having the unknownsA0,A1,A2,...,AN.
•Putting Eq.(13) in Eq.(11) along with Eq.(12) and setting Eq.(11) together with constantsA0,A1,A2,...,ANin Eq.(14),we extract the soliton solutions of Eq.(9) with the assistance of computational packages.
4.2.Description of MKM [59]
•We proceed on considering the solutions of (9) in shape ofQ(ξ) as
whereAi(i=0,1,2,3,...,N) are constants to be determined,Nis a positive constant andQ(ξ) is defined as
Eq.(16) satisfies a first-order nonlinear equation as
•Eq.(9) yields theN.The homogeneous balancing concept aids in equating the nonlinear terms in Eq.(9) with higher derivatives.(15) can be written as forN=1.
•The constantsA0,A1,A2,...,ANcan be obtained by substituting Eq.(15) into Eq.(9) and equating the coefficients ofQ(ξ)ito zero.
•Putting Eq.(16) in Eq.(15) along with Eq.(17) and then putting Eq.(15) along with constantsA0,A1,A2,...,ANin Eq.(18),The soliton solutions of Eq.(9) with the help of computational packages will be determined.
4.3.Description of NEDAM [60]
•Assume that the solution to Eq.(9) can be expressed by a ploynomialΩ(η)in the following form.
whereΛi(0≤i≤N) are constants to be determined andΩ(η) satisfies the following ODE,
The Eq.(20) has different solutions for detail see reference[60].
•The value ofNin Eq.(19) will be determined by balancing the highest-order derivative and nonlinear terms in Eq.(19).
•A set of algebraic equations are easily obtained by substituting Eq.(19) and its derivatives into Eq.(9) and equating coeffi-cients of the same power ofΩ(ξ) to zero.Upon tackling set equations with Mathematica’s assistant,we obtain the necessary unknowns and thus the desired solutions.
5.Extraction of solutions
This section discusses how to apply the proposed methodologies to demonstrate that our methods are effective,helpful,and simple.As a result,we discover a number of soliton solutions to the FWBBM equation.The following transformation can be used[72]
Integrating the above equation on keeping the constant of integration to zero,we get
Now,our concern to analyze the Eq.(23),and find its various solutions by applying the proposed computational techniques.
5.1.Solutions via KM
We getN=1 using the balancing principle.As a result,the solution of Eq.(23) can be referred to as Eq.(14).The following nonlinear algebraic system is generated by substituting Eq.(14) into Eq.(23) and then equating the coefficients ofQi(ξ) to zero:
This system of equations from (24) to (27) is solved with the help of computational packages to get following sets:
Set 1.
Substituting Eq.(13) in Eq.(11),we get
Now,putting Eqs.(28) and (29) into Eq.(14),we have
Set 2.
Substituting Eq.(13) into Eq.(11),and then putting Eqs.(11) and (31) into Eq.(14),we have
Now,putting Eq.(32) into Eq.(6),we have
Set 3.
Substituting Eq.(13) into Eq.(11),and then putting Eqs.(11) and (34) into Eq.(14),we have
Now,putting Eq.(35) into Eq.(6),we have
5.2.Solutions via MKM
On manipulating the Eqs.(18) and (23) and taking coefficients ofQi(ξ) to zero,we get:
This system of equations from (37) to (40) is solved with the help of computer packages to get following sets:
Set 1.
Substituting Eq.(16) along with Eqs.(17) and (41) into Eq.(18),we have
Also,Eq.(42) can write as
Substituting Eq.(16) along with Eqs.(17) and (44) into Eq.(18),we have
Also,Eq.(45) can write as
Substituting Eq.(16) along with Eqs.(17) and (47) into Eq.(18),we have
Also,Eq.(48) can write as
The graphs of obtained solutions with suitable parameters are sketched below
5.3.Solutions via NEDAM
By balancingς3(ξ) andς′′(ξ) in Eq.(23),we obtainN=1.Thus,the solution to Eq.(23) is as follows:
On manipulating the Eq.(50),we get the following family as:
Family-1.
The solutions to Eq.(6) are summed up below.
• Forχ2-4σ δ <0 andδ0,we explicitly secure the following results
The above solutions are valid under the conditions,Ξ1-Ξ4>0,Ξ2>0 andΞ20.
• Forχ2-4σ δ >0,δ0,numerous precise solitary solutions are deduced.
The kink-type soliton solution
The singular soliton solution
The complex kink-bell type soliton solution
The mixed singular soliton solution
The explicit solitary wave solution
The above solutions are valid under the conditions,Ξ1-Ξ4>0 andΞ20.
• Forσδ >0 andχ=0,We get
The traveling wave solution
The explicitly singular periodic solution
The combined-trigonometric solutions
The validity conditions for above solutions are defined as,Ξ1-Ξ4>0,Ξ2>0 andΞ20.
• Forσδ <0 andχ=0,we secure The shock-type wave solution
The hyperbolic function solution
The complex combo soliton in different shapes
The validity conditions for above solutions are defined as,Ξ1-Ξ4>0, andΞ20.
• Forχ=0 andδ=σ,as a result,the periodic solutions are disclosed
• Forχ=0 andδ=-σ,We obtain various types of solutions.
The shock-type wave solution
The explicit hyperbolic function solitary wave solution
The combined complex soliton-like solution
The combined singularity soliton solution
The explicit hyperbolic function solitary wave solution
The validity conditions for above solutions are defined as,Ξ1-Ξ4>0, andΞ2<0.
• Forσ=0 andχ0,exponential function solution is extracted as:
• Forσ=0,χ=κandδ=rκ,the plane wave solution is
The graphs of obtained solutions with suitable parameters are sketched below
6.Conclusions
This section concludes with a discussion of our findings and a comparison to previously published work.The 3D-FWBBM equation has been approached from a variety of angles in published work.For instance,Aly R.Seadawy et al.[72] extracted a variety of soliton solutions using straightforward ansatzes.Several soliton solutions had been discovered in Kaabar et al.[73] using expansion function and generalised Kudryashov methods.The governing model was analysed,and various travelling wave solutions were obtained using symbolic computation [74].Exact singular,solitary,and periodic singular wave solutions were obtained using the-expansion function method[75],whereas general solitary wave solutions in terms of generalised hyperbolic and trigonometric functions were discussed [76].Three novel methods called,modified F-expansion,generalized direct algebraic,and improved simple equation were used to analyze the modified BBM equation for securing dispersive soliton solutions for shallow water wave system [77].A variety of explicit traveling wave solutions of the coupled BBM-KdV equation were found out by using the modified-expansion method [78].Moreover,the 5th-order KdV equation was discussed by modified simple equation method and conservation theorem [79].Furthermore,when the comparison process is implemented between our achieved solutions by these applied methods and that achieved previously by various techniques it shows that few types of the obtained solutions agree with that realized before and the majority is new,this denotes to the novelty of our achieved solutions.
Additionally,we examined various wave patterns in terms of their exact solitary wave solutions,including kink-type,singular,shock,combo and complex solitons,in relation to the recently designed conformable 3D Wazwaz–Benjamin–Bona–Mahony model,which is used as the governing model for propagation of waves in shallow water.Besides that,we assure solutions for functions that are hyperbolic,periodic,or exponential.The results of the paper may assist in clarifying the true character of numerous nonlinear advancement situations that arise in a variety of nonlinear sciences domains.Among the many applications of hyperbolic functions are: computation and speed in special relativity;the Langevin function for attractive polarization;a chamber’s gravitational capabilities and an estimate for its maximum gravitational capacity;and the profile of a laminar jet.The physical movements of identified solutions are charted in 3D,2D,and contour in Figs.1–9 by setting specific parameters.The outcomes to three-dimensional FWBBM model can be implemented to another nonlinear water model equations in ocean and coastal engineering to demonstrate the potential of the computational techniques.Additionally,our study results open the way for a better understanding of complicated model’s structure and physical behavior.Our findings,we anticipate,will significantly contribute to our understanding of the waves that occur in nonlinear complex models.We believe that this work is timely and will be of interest to a broad range of experts involved in modeling.By substituting the secured answers back into the original problem,computation packages are used to verify all of the secured answers.
Declaration of Competing Interest
Authors declare that they have no conflict of interest.
Acknowledgments
The authors would like to acknowledge the financial support provided for this research via Open Fund of State Key Laboratory of Power Grid Environmental Protection (No.GYW51202101374),the National Natural Science Foundation of China (52071298),Zhong Yuan Science and Technology Innovation Leadership Program (21420 0510 010).They also thank the reviewers for their valuable reviews and kind suggestions.
 Journal of Ocean Engineering and Science2023年5期
Journal of Ocean Engineering and Science2023年5期
- Journal of Ocean Engineering and Science的其它文章
- New solitary waves and exact solutions for the fifth-order nonlinear wave equation using two integration techniques
- Numerical treatment of temporal-fractional porous medium model occurring in fractured media
- Optimal Kalman-like filter for a class of nonlinear stochastic systems
- Dynamic quantitative risk assessment of LNG bunkering SIMOPs based on Bayesian network
- New soliton wave solutions of a (2+1)-dimensional Sawada-Kotera equation
- Review of enhancement for ocean thermal energy conversion system
