基于确定初始簇心的优化K-means 算法
喀什大学计算机科学与技术学院 岳珊 雍巧玲
考虑到K-means 聚类算法在聚类过程中同等地看待每个特征维度、簇心的初始选取是随机的等问题,采用优化K-means 算法SVD-Kmeans。首先对高维样本数据采用奇异值分解方法,在最大限度保证原始样本数据特征的前提下进行降维处理,每个样本降维后得到一个二维指标值,再使用初始簇心求解模型确定初始簇心的选取,最后通过K-means 算法进行聚类求解,形成最终模型。通过在同一数据集上实验发现,采用SVDKmeans 算法相较传统K-means 聚类算法准确率提高34.24%左右。
K-means 聚类算法是由J.B.MacQueen 提出,该算法是一种迭代求解的聚类分析算法,该算法具有原理简单、容易实现、可理解性较强等优势,但也存在容易出现局部最优、聚类效果依赖于聚类中心的初始化等问题。
基于此,学者们从两方面进行改进优化,一方面使用该算法与其他算法混合使用[1-3];另一方面从优化算法本身上下功夫,如目前使用较多的K-means++算法[4-8]、二分K-means 算法[9-13]等。然而,这几种优化方案虽然解决了簇心数量确定、减少算法时间、防止局部最优等问题,但仍然不可避免地存在实验之初随机选择一个样本点作为第一个初始化的聚类中心的问题。
基于以上考虑,本文首先对高维数据进行降维处理,解决算法同等看待每个特征维度的缺陷,再使用簇心求解模型首先确定两个簇心的初始位置,最后使用K-means算法对样本进行聚类操作,通过以上操作,有效地避免了实验之初簇心随机选取和K 值不确定的问题。
1 K-means 算法研究
K-means 算法能够在不知道任何样本标签的情况下,通过数据之间的内在关系将样本分为若干个类别,使得相同类别样本之间的相似度高,不同类别之间的样本相似度低。
通过迭代的方式寻找k 个簇的划分方案,使得聚类结果对应的代价函数最小,如式(1)所示:
其中,xi代表第i个样本,ci是xi所属的簇,μci代表簇对应的中心(即均值),N是样本总数。
2 原始数据处理
选用机器学习MLP 填充方法对数据集中的缺失值进行填充,应用拟合与分类思想,将不含缺失值的行作为训练样本的输入和标签,缺失值的行(不含缺失值的部分)作为测试样本的输出,缺失值即是测试样本的待预测标签,填充结果如图1 所示。

图1 缺失信息填充Fig.1 Missing information filling
此次试验共填充177 名乘客的年龄信息,其中纵坐标代表乘客的年龄,通过结果分析发现大部分年龄集中在20 ~30 岁之间。
3 SVD-Kmeans 算法
3.1 降维处理
输入:N 个样本。
输出:一个N×R 矩阵。
(1)对高维矩阵进行奇异值分解得到矩阵V,如式(2)所示:
(2)以矩阵V 的前D列作为降维矩阵,用高维矩阵和V '做矩阵乘法,实现降维,如式(3)所示:
3.2 簇心求解模型
3.2.1 模型假设
(1)簇心作用强度向其四周等强度扩散;
(2)簇心作用强度服从扩散定律,即单位时间影响单位法向量的面积与它的强度梯度成正比。
3.2.2 模型建立
将簇心起作用的时刻记为t=0,簇心点首先选为坐标原点。时刻t无穷空间中任一点(x,y)的强度记为C(x,y,t)。根据假设2,单位时间通过单位法向面积的强度扩散面积,如式(4)所示:
k为扩散系数,grad表示梯度,负号表示由浓度高向浓度低的地方扩散。考查空间域Ω,Ω 的体积为V,包围Ω 的曲面为S,S的外法线向量为n,则在[t,t+Δt]内通过Ω 的强度如式(5)所示:
而Ω 内强度的增量如式(6)所示:
质量守恒定律如式(7)所示:
将数据集中所有数据作为簇心,求解每个点的扩散强度和扩散增量,最大的两个即为本次实验的初始簇心。
3.3 聚类算法
输入:N 组样本数据。
输出:待分类样本所对应的分类结果。
(1)使用簇心求解模型求解出的两个初始簇心,记为μ1,μ2。
(2)计算每个样本xi到各个簇心的距离,将其分配到与它距离最近的簇。
(3)对于每个簇,利用该簇中的样本重新计算该簇的中心(即均值向量)。
(4)重复迭代上面2 ~3 步骤T 次,若聚类结果保持不变,则结束。
4 实验介绍
通过奇异值分解方法尽可能多的保留原始样本的数据特征得到降维后的矩阵,在本实验中,N=94,M=49,D=2。本次实验各奇异值的贡献率如下所示:
第1 个奇异值的累积贡献率是:0.20299414497066245
第2 个奇异值的累积贡献率是:0.4010049338627624
第3 个奇异值的累积贡献率是:0.5514842977877248
第4 个奇异值的累积贡献率是:0.6884462710597125
第5 个奇异值的累积贡献率是:0.8034632384325324
第6 个奇异值的累积贡献率是:0.9120410189148603
第7 个奇异值的累积贡献率是:1.0
奇异矩阵为:
降维后的数据结构如图2 所示。

图2 降维结果Fig.2 Dimension reduction results
根据数据集特征可知最终确定出2 个簇心,根据簇心公式确定簇心后,使用K-means 方法进行聚类,如图3 所示。
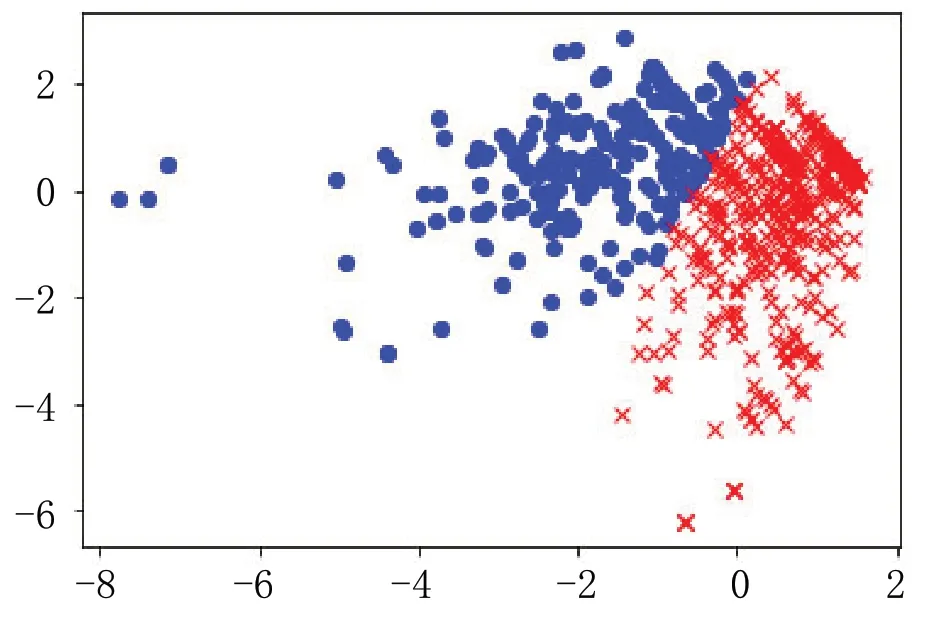
图3 优化K-means 算法聚类结果Fig.3 Optimize K-means algorithm clustering results
在同一数据集上分别进行K-means 算法和SVDKmeans 算法聚类研究,计算两种算法聚类准确率如图4所示。
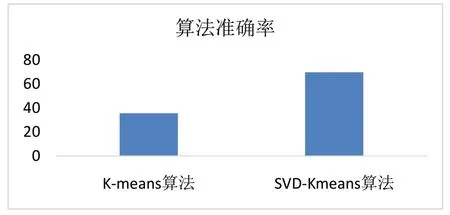
图4 两种算法准确率对比Fig.4 Comparison of accuracy between two algorithms
经过对比实验发现,传统K-means 算法的准确率为0.3557800224466891,SVD-Kmeans 算法的准确率为0.6980920314253648。
5 结论
通过在数据集进行K-means 聚类算法优化研究,发现当直接使用K-means 算法进行聚类时,准确率只有35.57%,考虑到K-means 算法自身存在的问题,提出优化K-means 算法模型SVD-Kmeans。首先使用奇异值分解方法对数据对象进行降维处理,再使用簇心求解模型确定出两个初始簇心,然后使用传统K-means 算法进行聚类研究,通过在同一数据集上再次使用,发现本模型的准确率得到大幅度提升。

