基于电力大数据的铝行业价格分析与预测

胡传胜 杨鑫 张永钦

1.安徽继远软件有限公司；2.上海韬牧投资管理有限公司；3.北京天易数聚科技有限公司

为探索基于电力大数据的行业经济分析预测，本文选取铝行业的用电量数据以及该行业的产品价格数据作为研究因子，首先通过相关性检验确认研究因子的相关性程度，在研究因子相关性较高的前提下，利用SVR 算法搭建基于行业用电量数据的铝行业价格分析预测模型，开展铝行业的发展趋势及市场价格分析预测。通过与实际情况进行对比，检验该模型对铝行业未来价格走势的预期效果，有利于投资者更加了解市场走势，有助于行业投资风险的分析决策，规避一些可控制的市场风险。

铝是我国仅次于钢铁的第二主要金属，在我国各个行业的应用中都是占有非常重要的作用。随着我国国民经济高速增长，预计今后20 年中，我国对铝的需求仍将处于增长阶段。由于受到铝的市场行情以及国际国内经济市场的多种因素影响，铝的价格波动很大。因此，对铝价格波动情况的分析以及对铝价格行情进行科学的预测，对于铝工业发展具有极其重要的意义。

当前电力行业与众多产业存在相互依存、相互影响的关系，通过电力数据可以间接分析产业的变化趋势，针对铝行业分析中对数据高频高质的客观要求，通过电力数据与铝行业经济数据的关联分析，充分发挥电力数据准确性高、实时性强、价值密度大、采集范围广等优势，助力提升铝行业价格预测的时效性和准确性。

本文选取2019 年1 月至2022 年8 月铝行业的用电数据及价格数据，基于相关性检验、SVR 算法构建基于电力数据的铝行业宏观基本面分析模型及价格分析模型，开展电力数据与铝行业经济数据的因果及趋势分析。

1 铝行业相关性分析

1.1 相关性算法介绍

相关性分析(Correlation Analysis)是指对两个或多个具备相关关系的变量进行线性相关分析，从而衡量变量间的相关程度或密切程度。相关性程度即为相关性系数r，r的取值范围是[-1,1]，相关性不等于因果[1]。

Pearson(皮尔逊)相关系数是反映两个变量线性相关程度的统计量，适用于变量满足连续性、正态分布性、线性关系[2]。

两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商，如式（1）所示：

式（1）定义了总体相关系数，常用希腊小写字母ρ作为代表符号。估算样本的协方差和标准差，可得到皮尔逊相关系数，常用英文小写字母r代表，如式（2）所示：

r亦可由(Xi,Yi)样本点的标准分数均值估计，得到与上式等价的表达式，如式（3）所示：

Spearman(斯皮尔曼）相关系数是衡量两个变量的依赖性的非参数指标，适用于定序变量或不满足正态分布假设的等间隔数据[3]。它利用单调方程评价两个统计变量的相关性，如果数据中没有重复值，并且当两个变量完全单调相关时，斯皮尔曼相关系数则为+1 或-1。常用希腊字母ρ表示，如式（4）所示：

实际应用中，变量间的联结是无关紧要的，于是可以通过简单的步骤计算ρ。被观测的两个变量等级的差值ρ，如式（5）所示：

进行基于电力数据分析预测铝行业的价格趋势的首要条件为确定铝行业用电量数据与价格数据是否存在强相关性，确定用电量是否为铝行业价格的重要预测影响因子。利用铝行业的用电数据及价格数据，并通过计算两组时间序列的皮尔逊相关系数和斯皮尔曼相关系数，观察系数大小，判别两组数据的相关性程度。

1.2 相关性分析数据处理

主要数据为2019 年1 月至2022 年8 月铝行业的用电数据及价格数据，对于铝行业价格数据存在的质量问题，例如：缺少个别月份的价格数据，采用KNN（最近邻）算法对于缺失数据进行估算补充。

为保证分析结果的准确性，分别通过计算皮尔逊系数和斯皮尔曼系数对于两组数据变量进行相关性分析，计算皮尔逊相关性的前置条件为两个变量之间需要存在线性关系或正态分布，接下来将分别通过K-S 检验和绘制散点图、直方图的方式进行检验数据是否满足前置条件。

对于小样本数据，通过K-S 检验方法，分别计算两组数据的p值，如果p值大于0.05，则证明数据满足归零的假设，即样本数据的总体分布服从正态分布，如果p值小于0.05，则反之。K-S 检验结果如表1 所示：

表1 K-S 检验结果表Tab.1 K-S test results table

通过对于原数据进行绘制散点图进行直观判断数据是否满足线性关系或正态分布，数据图如图1、图2 所示。

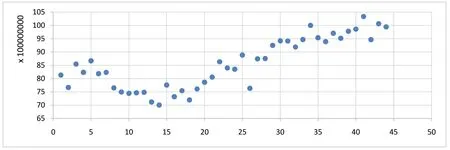
图1 铝行业用电量散点图Fig.1 Scatter plot of electricity consumption in the aluminum industry

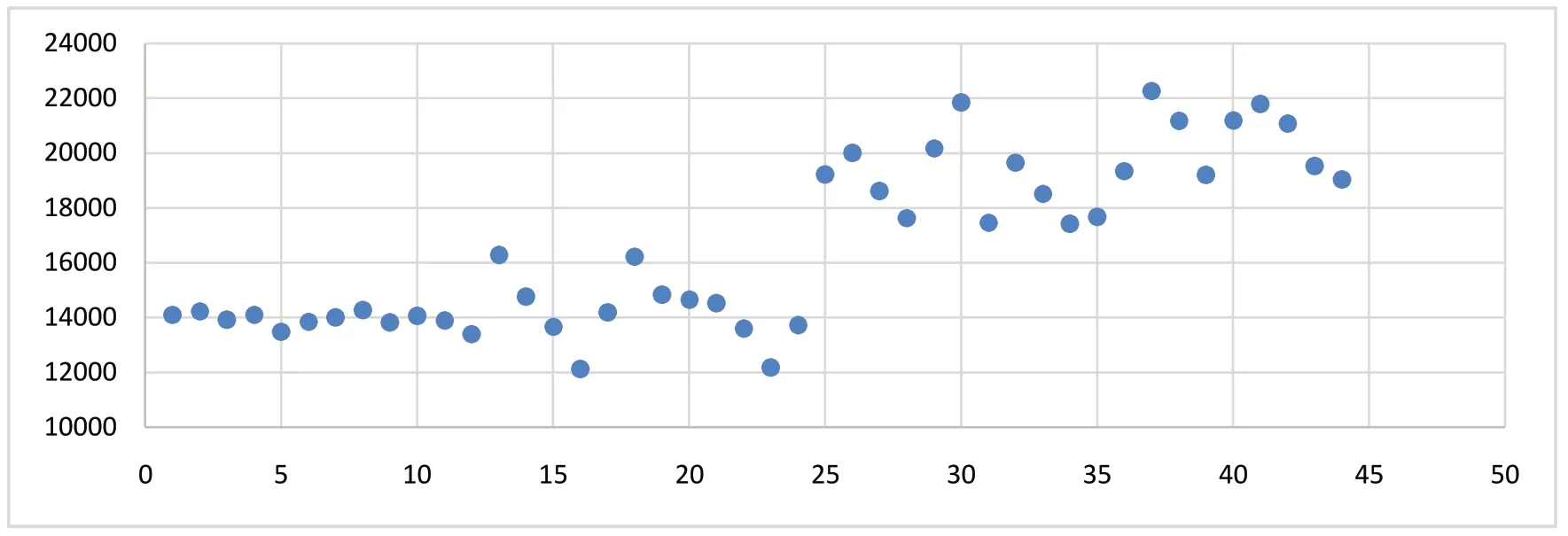
图2 铝价格散点图Fig.2 Aluminum price scatter plot

通过K-S 检验和绘制图形的方式，皆可验证原始数据满足正态分布的前提，接下来通过计算相关性系数判断数据相关性程度。

1.3 行业用电量与价格分析

将行业用电量数据、行业价格数据作为变量分别计算皮尔逊系数和斯皮尔曼系数，结果如表2 所示。

表2 相关性系数结果表Tab.2 Correlation coefficient results table

通过表2 可以看出，铝行业与其对应的铝产品价格所得的皮尔逊系数和斯皮尔曼系数皆大于0.5，都呈现正相关性且相关程度较高。

1.4 相关性分析结论

对原始数据进行KS 检验后，行业数据符合相关性检验的要求，通过计算皮尔逊、斯皮尔曼系数，比较两个系数与0.5 的大小可以得知：在现有数据的基础上，铝行业的用电量与铝的价格呈正相关性且相关性程度较高，所以对于铝行业的价格分析，可以发现铝行业的用电量将会是其重要的影响因子。

2 基于SVR 算法的行业价格预测分析

2.1 SVR 模型介绍

算法模型中的SVR，是非常“宽容的”一种回归的算法模型。支持向量回归模型的算法模型函数，归根结底就是一个线性函数：y=ωx+b，与线性回归的区别在于SVR用函数预测计算损失的基本原则是不同的，而且它的函数算法的优化方法也不相同。如，SVR 算法函数y=ωx+b在它的两边，用算法计出了间隔距离，在所有间隔距离内的样本点，计算的过程中将忽略其损失，间隔距离之外的样本点（红圈样本），计算的过程中才会加入函数中，损失为样本点到间隔带边缘的投影与样本点y值的差，使得间隔距离之间的宽度，函数的总损失能达到最小化，以此来优化改善算法模型。模型函数为：y=ω·φ(x)+b。

SVR 利用核函数将原始数据向高维映射，有效解决非线性问题，且SVR 结果由少数支持向量决定，适用于小样本数据集，且具有较好的鲁棒性[4]。

2.2 算法模型搭建

基于相关性分析和因果检验分析的结果，铝行业的用电量、价格相关性程度较高，且结果表明铝行业用电量为影响铝价格的重要因素，在不考虑到资源禀赋、供求关系、投机等因素的影响下，采用铝行业用电量作为预测铝价格的主要影响因子，利用SVR 算法搭建铝价格预测模型。

2.2.1 数据平稳化

原始序列分别为内部的电量数据以及外部权威机构（wind 等）获取的铝价格数据，时间维度为2019 年至2022 年9 月，数据频度为日频，铝价格的原始数据趋势情况如图3 所示。

图3 铝期货价格历史趋势Fig.3 Historical trend of aluminum futures price

通过对原始序列进行快速的平稳性的检验，采用ADF 检验和KPSS 检验。原始序列检验结果为ADF=0,KPSS=1，结果显示原始序列不符合平稳性要求，对原始序列进行一阶差分，差分后序列ADF=1，KPSS=0，符合平稳性要求，利用一阶差分序列的结果，进行后续建模，即模型参数d=1。

2.2.2 模型检验

模型确定后，通过绘制残差检验结果图进行模型检验.残差指的是实际观察的指数值与预估值之间存在的差。残差检验结果如图4 所示，蓝色的点已经趋近中间的直线，残差符合正态分布。

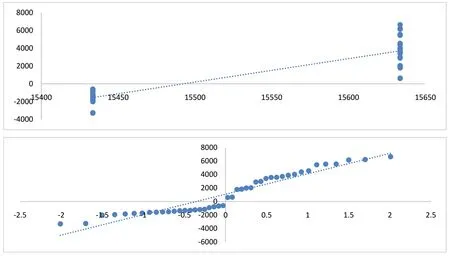
图4 模型检验结果图Fig.4 Model test results

2.3 预测

在铝行业用电量与铝价格的预测分析中，基于SVR算法，利用2019 年至2022 年9 月的铝行业用电量与铝价格数据进行拟合预测，数据频度为月频，预测结果如图5 所示，预测结果平均误差率为9.3%。

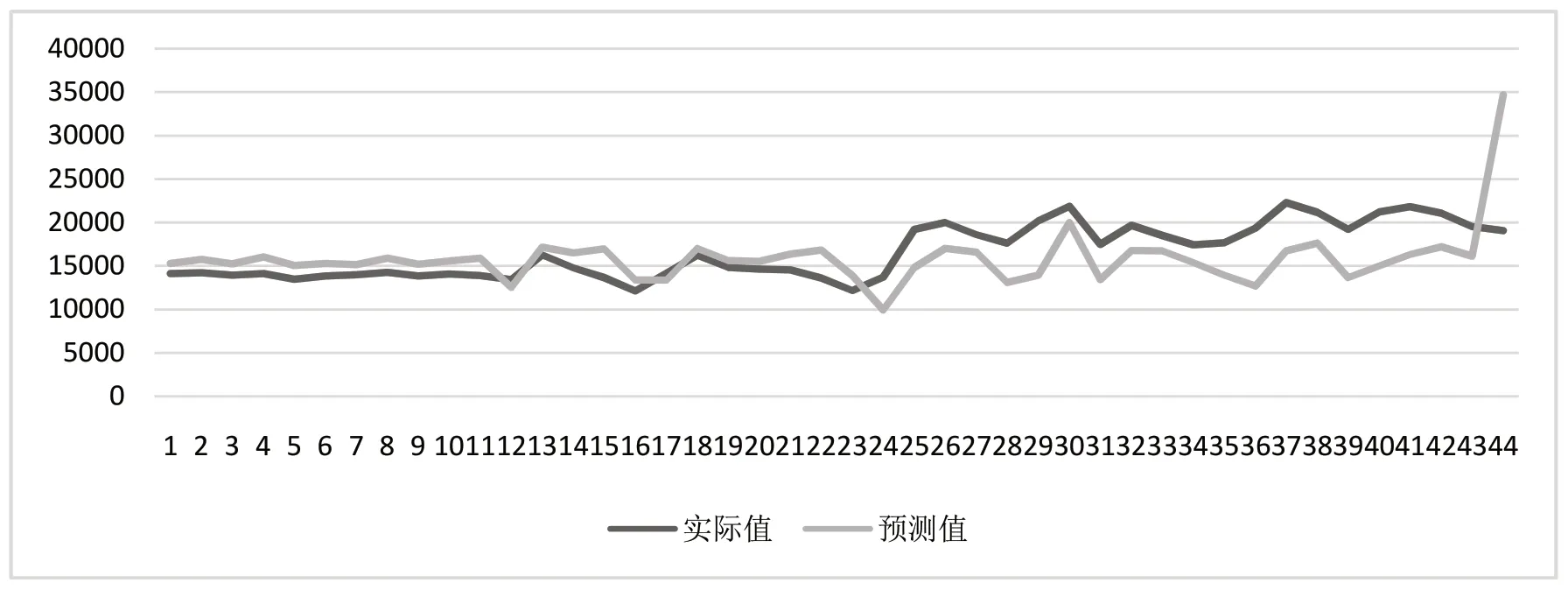
图5 铝价格预测结果图Fig.5 Aluminum price forecast results

3 结语

从铝行业的影响因素看，尽管行业用电和铝价格相关性较大，但影响铝价格因素的不仅仅只有产业用电，还有其他影响因素，包括生产工艺、汇率波动、供需关系、政策因素等，后期考虑从多个维度进行关联分析。在算法提升方面，通过SVR 算法模型预测到的结果可看出短期内的精度较高，今后可进一步将粒子群优化算法与神经网络方法结合使用，同时在考虑多个维度的情况下，搭建铝冶炼行业价格预测模型。