纳秒脉冲激光辐射黑火药的光声信号快速检测方法及分析

陈奕如，沈瑞琪，吴立志

（1.南京理工大学化学与化工学院，江苏 南京 210094； 2.微纳含能器件工业和信息化部重点实验室，江苏 南京 210094）

0 引 言

含能材料的激光点火一直以来备受研究者的关注，但激光点火机理的研究目前还不甚完备［1-4］。在激光点火的机理分析中，将激光视为热源，基于热化学理论对反应过程进行分析的思路最为常见［3，5］。此思路下，常用的辅助分析方法是基于热分析结果对激光辐照下含能材料的反应机制的探讨［6-7］。但是，热分析的升温速率对测试结果存在明显影响［8-9］，差热分析法（DTA）和差示扫描量热法（DSC）等热分析方法的升温速率通常不超过1 K·s-1，远远小于含能材料实际点火过程中的升温速率［10］。许多现象也无法通过热化学理论解释，例如，依据热化学理论计算所得的激光点火阈值较实测值低1 至2 个数量级［1］；热化学理论表明吸光率高的含能材料更易被激光点燃，但是实验表明，部分含能材料的吸光率与激光感度缺乏明确的关系［4］，因此，采用不同于热分析的方法对含能材料与激光的相互作用过程进行观测和分析十分必要。

1880 年，Bell［11］在 研 究 中 意 外 发 现，物 质 在 受 到强度经过调制的阳光照射时会有声音产生，这种现象被称为“光声效应（photoacoustic effect/optoacoustic effect）”，光声效应产生的声信号被称作“光声信号（photoacoustic signal/optoacoustic signal）”，对其进行研究的学科则被称作“光声学（photoacoustics/optoacoustics）”［12］。光声信号的生成和传播特性与被辐照材料的特性息息相关，因此，通过分析材料的光声信号可以实现对材料物性的检测［13］。基于光声效应的检测方法具有装置简单可靠［14］，可测样品种类丰富［15］等优点，因此在化学物质的谱分析［16-17］、含能材料的探测［18-19］、含能材料的热化学反应动力学分析［20-21］等领域均有应用。

传统的光声学研究通常只关注系统的稳态性质［16-19］，南京理工大学沈瑞琪团队［22］将光声信号的瞬态变化纳入考虑，建立了含能物质的反应性光声谱理论（reactivity photoacoustic spectroscopy，RPAS），并将该理论应用于含能材料的快速化学反应过程探测［23-24］、含能材料的激光点火过程分析［7，25-26］，以及推进剂的超快热损伤分析［27］等研究中，取得了初步的研究成果。但是，沈瑞琪等［6，28］在研究中沿用了传统光声检测中常用的压电传感器与电容传感器，商用电容传感器的带宽通常不超过150 kHz，不适合检测快速变化的信号［29］；压电传感器的灵敏度大约在10 mV·kPa-1量级，难以准确检测弱信号［13，29］；传感器与被测介质的耦合也会导致被测信号的畸变［30］。上述误差阻碍了含能材料光声信号的定量分析。具备高精度、高频响、无接触检测等特性的激光干涉测量法弥补了上述缺点，近年来在声学研究中逐渐引起关注［31］。Chen［32］使用Michelson 式干涉仪测量了纳秒激光脉冲点源与非反应性材料相互作用所得的瞬态信号，发现线性声学理论足以定量描述脉冲激发的扰动，并且推导出了扰动的解析解，但是对于线性声学理论是否适用于描述反应性物质的光声信号，Chen 未做探究。

为此，本研究将基于超快声信号非接触干涉测量方法，以黑火药为被测物，检测纳秒脉冲激光引发的反应性光声信号，检验线性声学理论在反应性光声信号分析领域的适用性，分析光致黑火药反应的机制。

1 实验部分

1.1 试剂与仪器

试剂：石墨粉、升华硫、硝酸钾（化学纯，国药集团化学试剂有限公司）。

仪器：1064 nm脉冲激光器（定制，哈工大）；1550 nm连续激光器（N7711A 型，Keysight 公司，美国）；光电探测器（DET08CFC/M 型，Thorlabs 公司，美国）；激光能 量 计（PE25BF-C 型，Ophir Photonics 公 司，以 色列）；示波器（MDO4054C 型，Tektronix 公司，美国）；探头（定制，OZ Optics 公司，加拿大）；2×2 光纤耦合器（定制，OZ Optics 公司，加拿大）；相位调制器（LN65S/FC 型，Thorlabs 公 司，美 国）；信 号 发 生 器（33512B 型，Keysight 公司，美国）。

1.2 样品制备

样品为黑火药及其各组分单质KNO3、S、C。黑火药各组分质量比为经典比例［33］m（KNO3）∶m（S）∶m（C）=75∶10∶15。为提升样品黏结性并且降低潜在发火可能，实验中使用石墨代替炭粉。为保证叙述的简洁性，下文采用KNO3、S、C 指代硝酸钾、硫磺、石墨样品。黑火药、KNO3、S 和C 均压制为厚度0.5 mm，直径6.0 mm的 薄 片。压 药 密 度 依 次 为ρblackpowder=1.7 g·cm-3，ρKNO3= 1.8 g·cm-3，ρS= 1.4 g·cm-3，ρC= 1.5 g·cm-3。

1.3 实验原理及装置

实验原理如图1 所示。待测样品固定于由不锈钢制成的刚性平面。激光脉冲聚焦于样品表面，激发光声信号。光声信号轴对称扩张，并且在掠过干涉仪的检测光束时被记录（在图1 中，信号尚未扩张至检测位置）。信号激发点与检测点距离远大于样品厚度，故样品厚度可以忽略。在忽略样品尺寸的前提下，依据Jenot 的研究［34］，平面法向的干涉信号变化体现了大气压强变化，故干涉信号可用于表征样品光声信号的强弱。

图1 实验原理示意图Fig.1 Scheme of the experimental principle

实验装置示意图如图2 所示。Nd： YAG 脉冲激光（1064 nm，10 ns）经分光镜分束，聚焦样品表面，其中聚焦面积为0.33 mm2。作用到样品表面上的激光脉冲能量可通过在入射光光路上的衰减片调节，脉冲辐射持续时间和激光脉冲能量由光电探测器和激光能量计分别记录。脉冲激发的光声信号由干涉仪探头发出的光束和表面返回的光束经过干涉后进行检测，检测点与激发点距离6 mm，检测激光为连续的1550 nm 单频激光，检测光斑直径10.5 μm。

图2 实验装置图解1—1064 nm 脉冲激光，2—1 号光电探测器，3—衰减片，4—激光能量计，5—1：1 分光镜，6—聚焦透镜，7—被测样品，8—刚性平面，9—探头，10—FC/PC 接头，11—相位调制器，12—信号发生器，13—2×2 光纤耦合器，14—2 号光电探测器，15—示波器，16—1550 nm 连续激光，17—计算机Fig.2 Illustration of the experimental setup1—1064 nm pulsed laser，2—photoelectric detector No.1，3—attenuator，4—laser energy meter，5—1：1 beam splitter，6—convex lens，7—measured sample，8—rigid plane，9—sensor head，10—FC/PC，11—phase modulator，12—signal generator，13—2×2 fiber coupler，14—photoelectric detector No.2，15—oscilloscope，16—1550 nm continuous laser，17—computer

实验所用的干涉仪是基于Dandridge［35］的解调方案的光纤式Michelson 干涉仪。仪器的配置参考Jia［36］和Thurner［37-38］的 光 纤 式Fabry-Pérot 干 涉 仪，并且进行了改进。在系统中引入相位调制器简化了装置，提高了系统稳定性。

光纤式Michelson 干涉仪的原理与传统的Michelson 干涉仪基本相同，二者的主要区别在于，光纤式干涉仪的光路几乎全部位于单模光纤内部，因此光纤式干涉仪相较于传统干涉仪，配置更为灵活，更不容易受到环境干扰。

1550 nm 连续激光经由2×2 光纤耦合器分束后，50%的激光被相位调制器调制，在FC/PC 端面处反射；剩余50%的激光自探头处射入自由空间，在刚性平面处反射，经由探头返回光纤。实验所用的探头是经过了抗反射处理的特制聚焦镜。自探头射出的连续激光束直径极小，故可近似认为连续激光束垂直于刚性平面。两束反射激光再度通过2×2 光纤耦合器，最终被2 号光电探测器检出。被检激光的光强I满足

式中，A和B为与连续激光初始光强和刚性平面反射率相关的常数，V；φ为未引入相位调制时两束反射光的相位差，rad；Dsin（ωt）为相位调制器引入的相位差；t为时刻，s；D为调制深度，rad；ω为角频率，rad·s-1。

利用雅克比-安格尔恒等式，式（1）可以展开为

式中，J为第一类贝塞尔函数。

不同频率的光强分量，使用锁相放大器即可一一分离。将分离所得的系数-2AJ1(D)sin(φ)记作Iω，2AJ2(D)cos (φ)记作I2ω，则φ值可由式（3）计算：

Thurner［38］的分析表明，干涉仪的时间分辨率与2π/ω大致为同一量级。本实验所用的信号发生器最大调制频率为20 MHz，适用于亚微秒尺度信号的检出工作。

实验时的环境温度为10 ℃。

2 结果与讨论

2.1 基于线性声学理论的回归分析

本节将基于回归分析验证既有理论的适用性，确定实验检得的干涉信号的物理意义。

图3 是实验装置中光声信号激发区域的局部放大，同时也是Chen［32］假设的系统初始状态示意图。Chen［32］在研究纳秒激光脉冲点源与非反应性材料的相互作用时，发现测得的干涉信号可以视作半径为b的轴对称初始扰动声波在空间中传播的结果。初始扰动的影响范围如图3 中浅蓝色区域所示，并且近似满足：

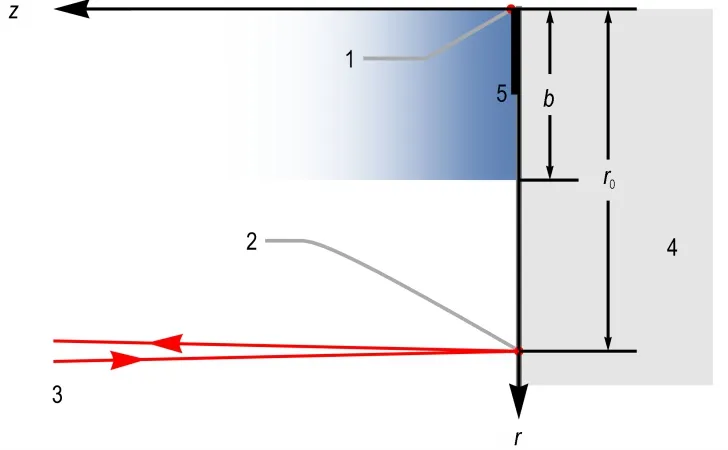
图3 模型初始状态示意图1—聚焦点，2—检测点，3—检测光束，4—刚性平面，5—样品Fig.3 Scheme of the model for the initial state1—source spot，2—detection spot，3—detection beam，4—rigid plane，5—sample

声扰动的传播服从线性声学理论［32］，以式（4）为初始条件，可以推导出声扰动的大小满足下述定量公式（5）：

式中，c0为声速，m·s-1；r0为聚焦点与检测点的距离，m，如图3 所示。

根据Chen［32］的分析，P正比于相位变化Δφ=φ-φ0，φ0为无扰动时的相位差，对于1550 nm 激光，在环境温度为10 ℃时，P与Δφ的关系为：

Chen 的模型是由非反应性材料的实验数据总结而来的，对于反应性材料，其适用性未知。为了验证Chen 的模型是否适用于描述黑火药及其各组分单质的光声信号，基于式（5）对实验数据做了线性拟合，结果如图4 所示，其中图4a 是典型拟合结果，图4b 是全体拟合结果的决定系数R2三维直方图。由图4a 及4b可知，式（5）与本研究的实验数据保持了较好的一致性，基于Chen 的模型解释本研究的实验结果是可行的。干涉仪检出的信号定量地描述了相对压强在垂直方向上的积分。为保证叙述的简洁性，下文仍将使用“光声信号”一词指代该信号。

图4 基于线性声学理论的拟合结果分析Fig.4 Fitting analysis based on the linear acoustic theory

由图4 还可看出，R2随激光脉冲能量的减小有下降趋势，因为对于较小的激光脉冲能量，干涉信号的信噪比也较低。激光脉冲能量与干涉信号强度关系的定量分析详见2.2 节。

综上所述，研究测得的光声信号可以使用式（5）定量分析。值得指出的是，式（5）的推导过程基于线性声学理论，因此不涉及温度场的变化；尽管c0等参数的计算涉及温度，在本节的回归分析中，与温度相关的参数均基于实验时的环境温度计算，这意味着本研究的实验结果与激光辐照引发的温度变化缺乏明确关联，难以参考黑火药的热反应机理［39-42］进行解释，但是，仅凭本节的分析无法确定黑火药在激光辐照下是否存在其他形式的反应。

2.2 光声信号特征分析

为了确定黑火药光声信号是否因化学反应发生了增强，本研究对光声信号的特征作定量分析。黑火药及其各组分单质在10 mJ 激光脉冲能量下的典型光声信号如图5 所示。由图5 可见，光声信号在数十微秒的时间内迅速出现又消失，信号特征较为简单。各组实验中干涉仪探测到的相位变化φ随时间的变化规律高度相似，但是不同样品的信号强度、起始时间及持续时间并不相同，其中KNO3的信号强度显著低于其他样品。所有信号均在脉冲激光发出后18 μs 左右由正转负，该时长与实验室环境温度下声波由信号激发点传播至检测点的耗时大致相同。此现象与Chen［32］的模型相符，因为根据Chen 的模型，初始扰动的传播速度恒为声速，而干涉信号的起始位置和零点分别是由初始扰动的边界和中心演化而来的。被测样品物性的改变会导致初始扰动边界位置的改变，但是不会影响扰动中心位置与检测点的距离，因此干涉信号的零点出现时刻不会有明显变动。

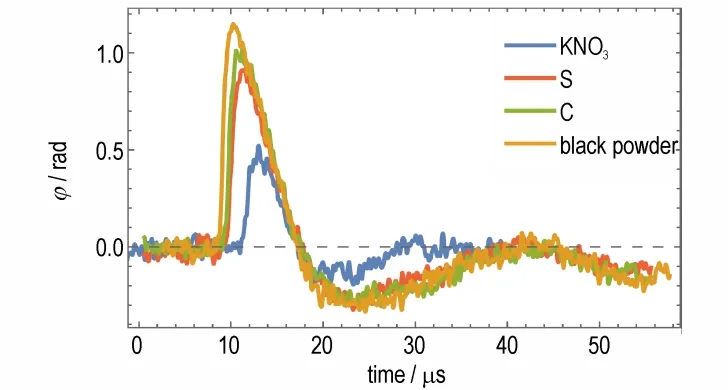
图5 10 mJ 激光脉冲能量下各样品的典型信号Fig.5 Typical signals under the irradiation of laser pulse with 10 mJ energy

为进一步定量分析所得信号，引入相位变化对时间的积分Φ作为分析对象。Φ的具体定义如式（7）所示：

式中，t0为信号由正转负的时刻，s。Δφ正比于P［32］，因此Φ与声信号正压区域的冲量在r方向上的分量成正比，可以用作衡量光声信号强度的指标。以Φ为纵坐标，激光脉冲能量为横坐标作图。拟合结果如图6所示。

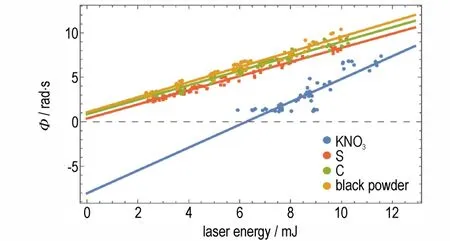
图6 Φ 与激光脉冲能量的关系（直线为线性回归结果）Fig.6 Relationship between Φ and laser pulse energy（the lines are obtained based on linear regression）

由图6 可见，Φ与激光脉冲能量近似呈线性关系。KNO3，S，C 和黑火药的线性拟合结果依次是

式中，Φ代表相位变化对时间的积分，rad·μs；E代表激光脉冲能量，mJ。由公式（8）可知，黑火药、S、C 的光声信号强度较为接近，但是仍有不可忽视的区别。

如果在激光辐照下，黑火药各组分间不存在相互作用，则黑火药的光声信号理应表现为各组分单质光声信号的加权平均：

式中，pKNO3、pS、pC的具体取值未知，但是均为非负数，并且pKNO3+pS+pC= 1。满足上述限制的加权平均数不会大于原始数据，因此由公式（9）计算所得的Φmean的斜率与截距不可能大于各组分单质，但是实验测得的Φblackpowder的斜率与截距均大于各组分单质。这表明黑火药各组分之间的化学反应对声信号存在贡献。值得强调的是，黑火药光声信号的增强无法用样品反射率的变化解释，因为根据Schatz［43］的研究，透明及非透明粉末的混合物反射率介于其单质组分反射率之间，或远低于各单质组分反射率。

2.3 声波能量估算及分析

实验测得的Δφ与基于式（6）简单换算所得的P的物理意义不够直观。研究基于实验数据估算声波蕴含的能量，以更清晰地呈现实验结果，降低实验结果的解读难度。

根 据Chen［32］的 测 量，相 对 压 强p在z方 向 的 分 布近似服从半正态分布

当P=25.7 Pa·m，r0=6 mm 时，σ=6.82×10-4m。假设σ的取值是可以推广至任意实验的常数，即可估算出声波能量。

根 据 线 性 声 学 理 论［44］，在 静 止 大 气 中，vr满 足式（11）：

式中，ρ0是静止大气的密度，量纲为长度-3·质量。

当r0不太小时，r0处的p可以使用出射边界条件［45］式（12）进行估算：

基于能流的声波能量式（14）［44］：

将式（10）（13）代入式（14），便可得到基于r0处能流的能量估算式（15）：

联立式（6）与式（15），即可由Δφ计算出Ewave。

受Arrhenius 方程k=启发，以计算 所 得的Ewave为纵坐标，相应的E为横坐标，使用式（16）作非线性拟合，结果如图7 所示。

图7 声波能量与激光脉冲能量的关系，曲线为非线性回归结果Fig.7 Relationship between wave energy and laser energy，the curves are obtained based on nonlinear regression

由图7 可见，基于式（16）获得的拟合曲线与声波能量计算结果保持了较好的一致性。基于公式（16）的KNO3，S，C 和黑火药的非线性拟合结果如式（17）：

式中，Ewave为声波能量，mJ；E为激光脉冲能量，mJ。

对公式（8）的分析依旧适用于公式（17）：激光脉冲在黑火药表面激发的声波中蕴含的能量无法表达为各单质组分的加权平均，而是强于各单质组分，并且这无法用样品反射率的变化进行解释［43］，这表明黑火药各组分之间的化学反应对声信号存在贡献。

式（16）具备与Arrhenius 方程相同的数学形式，因此其物理意义可以类比Arrhenius 公式进行解释：在脉冲激光引发的光化学反应中，激光脉冲能量E具备与热化学反应中的温度变化ΔT相似的地位。

2.4 激光脉冲作用下的黑火药反应速率估算

基于公式（17），在引入适当假设的前提下，可以估算出黑火药在激光脉冲作用下的反应速率。引入以下假设：

（a） 黑火药的化学反应发生并且仅发生在激光脉冲辐照药面的τpulse= 10 ns 时间内。

（b） 黑火药化学反应的能量完全转化成了大气中声波的能量。

（c） 黑火药在激光辐照下发生的化学反应可由以下反应式［33］描述。

（d）Ewave，blackpowder满足Ewave，blackpowder=Ereaction+Ecomponents，式中Ereaction是黑火药化学反应产生的能量，Ecomponents是黑火药样品中未参与反应的各单质组分对声波能量的贡献。

（e）Ecomponents满 足Ecomponent=pKNO3Ewave，KNO3+pSEwave，S+pCEwave，C，式中pKNO3，pS，pC依次是KNO3，S，C 在黑火药中的体积分数。

（f） KNO3，S，C 在黑火药样品中的压药密度与各单质样品压药密度相同。

由假设（a）（b）（c）可推出光致黑火药分解的平均反应速率为：

其中，Ereaction可由假设（d）（e）以及式（17）求得。由1.2节所述的压药密度以及假设（f），可得各组分体积分数依次为pKNO3= 0.71，pS= 0.12，pC= 0.17。计算所得的平均反应速率vreaction与激光脉冲能量E的关系曲线如图8 所示。由图8 可知，vreaction与E大致呈正相关，但是当E较大时，vreaction出现了轻微的下降，这一现象可以解释为Ereaction与Ecomponents所代表的反应发生了竞争。vreaction的最大值约为20 mmol·s-1，与之对应的E约为10 mJ。

图8 黑火药反应速率与激光脉冲能量的关系Fig.8 Relationship between reaction rate of black powder and laser pulse energy

3 结 论

为了加深对含能材料与激光的相互作用过程的认识，研究采用干涉测量方法，对黑火药在纳秒脉冲激光幅照下产生的光声信号进行了检测与分析，得到以下结论：

（1）纳秒级脉冲激光激发的黑火药及其单质组分的光声信号可以使用线性声学理论描述。

（2）黑火药在纳秒级脉冲激光辐照下的反应机理与其热分解机理没有明确关联。

（3）光声信号强度与激光脉冲能量近似呈线性关系。

（4）黑火药信号并非单质组分信号的加权平均，其中存在各组分之间化学反应的贡献。

（5）光致黑火药反应中的激光脉冲能量与黑火药热分解反应中的温度变化地位类似；基于测得的光声信号，可以估算黑火药反应速率，计算所得的反应速率与激光脉冲能量近似正相关，当激光脉冲能量较高时，黑火药的化学反应与各单质组分的反应出现了竞争。当激光能量为10 mJ 左右时，反应速率达最大值，约为20 mmol·s-1。