随机非线性系统的有限时间命令滤波输出反馈跟踪控制
赵军圣,赵雪静,孙宗耀
(1.聊城大学 数学科学学院,山东 聊城 252059;2.曲阜师范大学 自动化研究所,山东 曲阜 273165)
1 引言
许多化学过程和热处理的实际工业过程会受到各种随机扰动的影响,故可以被描述为随机系统。然而,随机扰动的存在可能会导致系统不稳定甚至使其性能变低。因此,如何针对随机系统设计控制器并分析系统的性能变得尤为重要。针对这一问题,文献[1-3]已经取得了重大进展。在系统稳定性分析过程中,对未知项的处理一直备受关注。模糊逻辑系统(FLS)和神经网络(NNs)常被用来处理未知函数和未知非线性项[4,5]。在这些工具的帮助下,自适应反步技术[6]已经广泛应用于各种随机非线性系统,例如随机严格反馈系统[7]、随机非严格反馈系统[8]、随机纯反馈系统[9]。
另一方面,上述控制方法都是基于传统的反步控制策略提出的,这就不可避免地存在虚拟控制器求导过程中“计算爆炸”的问题。为了解决这些问题,文献[10]提出了动态面控制(DSC)方法。然而,该方法并未消除由一阶滤波器引起的误差。为此,Dong等人[12]将命令滤波技术与自适应技术相结合,用于减少非线性系统中出现的滤波误差。随后,文献[13]结合反步设计提出了一种输出反馈模糊控制策略,有效地解决了具有参数不确定性的非线性系统的输出反馈控制问题。
有限时间控制[14]不仅具有响应快、高跟踪精度的优点,还可以使系统具有较好的抗干扰性能。考虑到实际工程的需要,文献[15]首次建立了有限时间控制方案。在文献[16]中,借助模糊逻辑系统或神经网络技术,解决了函数非线性问题,改进了非线性系统的有限时间稳定性理论。文献[17,18]总结了有限时间稳定性的定义和常用判据,并讨论了基于二阶滑动控制器的有限时间控制问题。随后,文献[19]进一步提出了半全局依概率有限时间稳定(SGFSP),并研究了有限时间稳定性判据。然而,到目前为止,在有限时间框架内对于具有不可测状态的随机非线性系统的稳定性分析还没有得到令人满意的结果。
受上述研究成果的启发,提出利用有限时间命令滤波技术代替传统的命令滤波技术,以实现对具有未知非线性函数的随机非线性系统的半全局依概率有限时间稳定(SGFSP)。因此,本文主要有两个方面贡献:
(1) 与文献[20,21]中已有的结果相比,本文在有限时间范围内考虑了具有随机扰动和未知非线性项的非线性系统。通过设计新的补偿项来解决随机非线性系统中一阶滤波器所引起的误差,克服了DSC控制方法的缺点,使系统能够获得更好的控制精度。该方法证明了闭环系统中的所有信号几乎处处都是有限时间有界的,并且跟踪误差在有限时间内几乎收敛到原点附近的邻域内。
(2) 针对现有方法的不足[22,23],本文提出了有限时间控制和命令滤波的方法,解决了随机非线性系统的输出反馈控制问题,实现了更快的收敛速度。同时,将模糊自适应控制技术与反步控制方法相结合,构造了自适应模糊跟踪控制器,降低了计算复杂度,保证了闭环系统获得更高的跟踪精度。
2 问题陈述
考虑如下不确定随机非线性系统
(1)
式中X=[x1,…,xn]T是系统状态,u≜xn+1和y(t)分别是系统输入与输出。fi(·)和gi(·)是非线性连续光滑的未知函数。ω表示r维标准布朗运动,定义在一个完备概率空间上,其增量协方差为E{dω·dωT}=φ(t)φT(t)dt,φ(t)是一个未知的增量协方差矩阵。
在接下来的设计过程中,需要如下假设。
假设2 对任意X1,X2∈Ri,存在常数λi,使得
‖fi(X1)-fi(X2)‖≤λi‖X1-X2‖,
(2)
式中‖·‖表示2-范数。
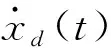
3 预备知识
下面给出本文用到的一些关键定义和引理。
定义1[23]对任意初始值x(t0)=x0,存在常数τ和驻留时间T(τ,x0)<∞,使得E[‖x(t;x0)‖]≤τ,即称随机非线性系统(1)的平衡点是半全局依概率有限时间稳定(SGFSP)。
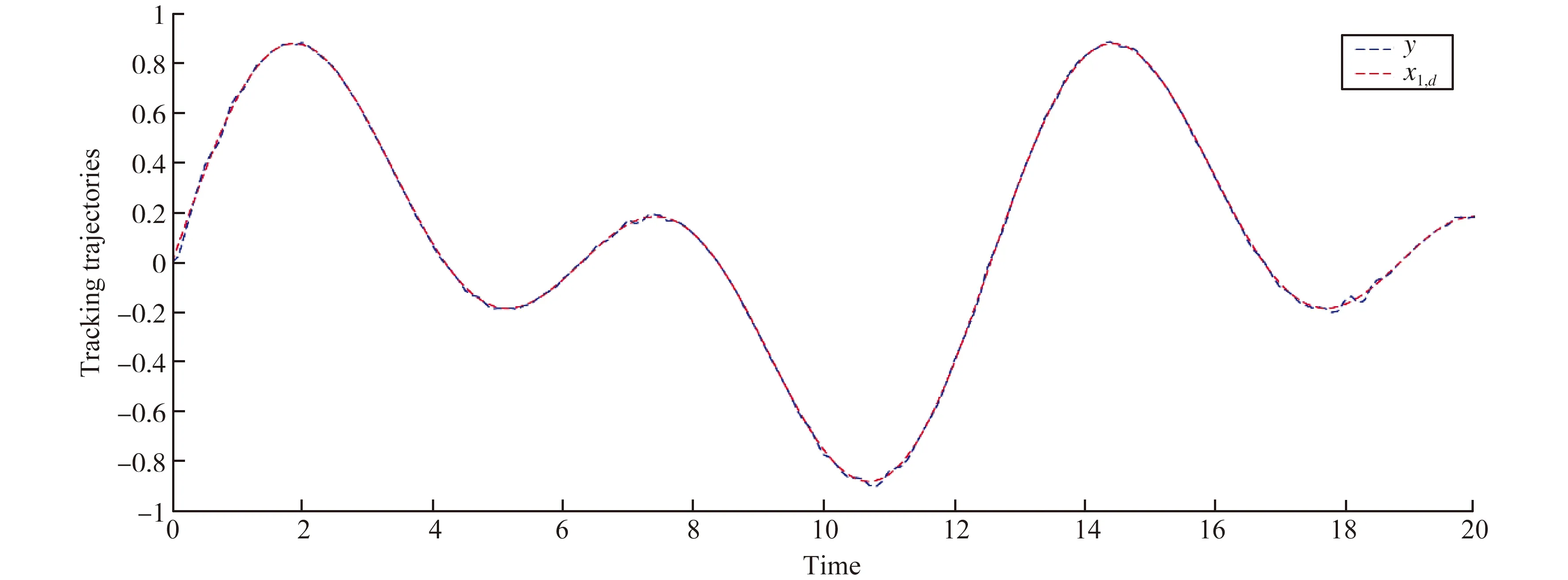
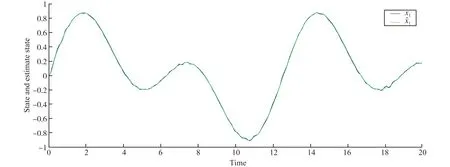
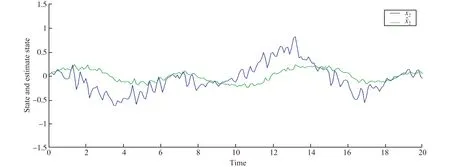
引理1[11]考虑随机系统(1)存在一个连续可微函数U(x),给定λ1,λ2∈K∞,存在常数c1>0,c2>0,0<ν<∞,0 引理2[11]令k>0,s>0,ε>0有以下不等式成立: 接下来,引入模糊逻辑系统的概念。 式中Ψk是使得模糊隶属度函数μAk(y)达到最大值的点,通常认为μAk(Ψk)=1。令 则模糊逻辑系统可以重新描述为y(x)=ΨTQ(x),式中Q(x)=[Q1,…,QN]T,Ψ=[Ψ1,…,ΨN]T。 引理3[11]经过有限时间瞬态过程,有如下不带有输入扰动的方程成立 (3) 式中ηr0=ηr并且解是有限时间稳定的。 注1 由引理3可知,如果噪声影响微分器的输入,则αr=ηr0成立,如果噪声不影响微分器的输入,则可以使用引理4。 引理4[11]如果输入扰动满足|αr-αr0|≤κ,借助适当的参数W1和W2满足 (4) 式中μ1>0,a1>0,ϖ1>0和ϖ2>0。 引理5[22]对于任意的ai∈R,i=1,…,n和给定的0 (|a1|+…+|an|)r≤|a1|r+…+|an|r≤n1-r(|a1|+…+|an|)r。 引理6[22]对于任意的ε>0和定义在紧集Ω上的连续函数χ(x),存在模糊逻辑系统ΨTQ(x),有 给出一阶Levant微分器 (5) 式中αr为输入信号,φ1和φ2为命令滤波的状态,W1和W2为待设计的参数。 现将系统(1)改写为以下形式 (6) 由于L是严格的Hurwitz矩阵,则存在两个矩阵DT=D>0和BT=B>0,有LTD+DL=-B。 选择李雅普诺夫函数V0=eTDe,并借助于引理6,假设1和假设2,可得 (7) 式中λmin(B)是B的最小特征值。 接下来,将阐述本文的主要结果。就(5)而言,对i=1,2…,n-1,定义有限时间命令滤波 (8) 式中xd是期望跟踪信号。为了处理由有限时间命令滤波引起的滤波误差,提出了如下形式的补偿机制 式中ξ(0)=0,这里ci,li是常数。 (9) 由引理2,不难得到 (10) (11) (12) (13) (14) 于是 (15) 定理1 设随机非线性系统(6)满足假设1~3,分别选择有限时间命令滤波器、补偿跟踪误差信号、虚拟控制器、实际控制器、自适应律,则闭环系统(6)是半全局依概率有限时间稳定(SGFSP)的,且跟踪误差依概率有限时间收敛到原点附近的邻域内。 证明从(15)中,可以得到 (16) 式中 除此之外,a=min{K1,K2,K3},b=min{K4,K5,K6}。此时,选择一个李雅普诺夫函数 可得 (17) 借助引理3和引理4,可以得到|xj+1,c-αj|≤ϖj1,于是有 (18) 注本文研究了有限时间命令滤波输出反馈跟踪控制问题,与文献[20,21]相比,将结果扩展到了随机非线性系统中。通过设计一个新的补偿项,克服了文献[10]中提出动态面控制方法的缺点,补偿了由一阶滤波器引起的误差。 作为设计方法的应用,考虑如下数值示例 (19) 构造虚拟控制输入和实际控制器 (20) 选择适当的自适应律 (21) 选择如下的设计参数的值 图1 y和xd的轨迹 图2 和的轨迹 图3 x1和的轨迹 图4 x2和的轨迹 本文基于具有随机扰动和未知状态的非线性系统的稳定性问题提出了一种模糊有限时间命令滤波反步控制策略,利用更为简易的状态观测器去估计测量状态,利用FLS技术估计未知函数。该方法不仅解决了中间变量函数多次求导引起的计算量大的问题,而且保证了有限时间内所有参考信号依概率有界。仿真结果表明了该控制方法的有效性。此外,该方法在输出函数未知的高阶随机非线性系统中是否具有可行性将是一个非常实际的课题。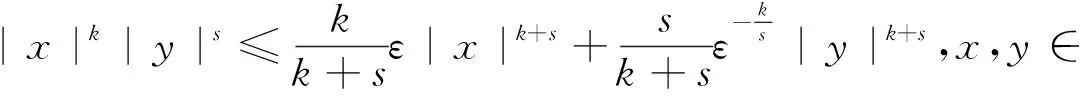

4 设计过程

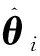
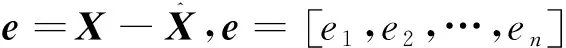
5 主要结果

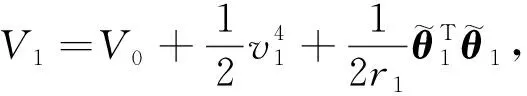
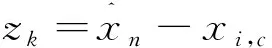

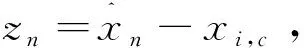

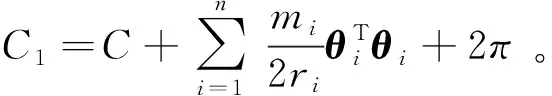
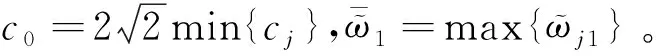
6 仿真例子
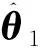

7 结论

