地下结构地震反应计算的Ritz 向量法

杨志恒 YANG Zhi-heng；陈攀 CHEN Pan；骆湘勤 LUO Xiang-qin；孙传海 SUN Chuan-hai；吴德汉 WU De-han

（北京城建勘测设计研究院有限责任公司，北京 100029）

0 引言

地铁车站构造复杂，其所处土层环境往往也很复杂，因计算机条件的限制，常采用二维模型进行地下结构抗震分析，为更深入研究地下结构地震反应规律，分析不同地震动场的综合影响，采用地下结构三维整体模型进行研究是很有必要的[1]。同样的原因，充分研究地下结构与邻近地表结构（群）的相互作用问题[2]和“城市效应”问题[3]时都需要建立三维有限元模型。

虽然个人计算机硬件发展较十年前有较大进步，但三维土层-结构动力分析模型的自由度很大，在运算的时候就会出现运算时间过长和内存不足的情况。因此，三维模型高效快速计算问题，是土层-结构系统动力相互作用分析模型推广应用所需要解决的关键问题之一[4]。

在快速高效计算方法发展方面，姜忻良研究了混合约束模态子结构法[5]。冯青松探索了约束模态综合法在商用软件ANSYS 平台上的实现[6]。

以上研究成果均表明约束模态子结构法能在保证计算精度的前提下有效提高计算效率。因该类型的子结构需求解n 阶广义特征值问题，对于大型结构，其迭代求解仍然花费较多的计算时间，若采用Ritz 向量代替模态向量可以进一步提高计算效率，因为获得Ritz 向量仅需解n 阶线性代数方程组。本文探索基于Ritz 向量法在结构动力分析中应用的可行性。

1 理论分析

Ritz 向量法先假设有这样一组比结构系统主模态集[Φm]相对来说更为有效的Ritz 向量基[X]=[x1，x2，…，xm]，则根据Rayeigh-Ritz 法，系统的位移动力响应可表示为：

通过递推求解可获得一组比模态向量更为有效的Ritz 向量基，递推求解步骤如下：

首先，根据外荷载{f（s）}求解得到拟静力反应{y1}：

将{y1}对质量阵[M]归一化后求得第一个Ritz 向量{x1}：

按照这种方法产生m 个Ritz 向量后，就可得出广义质量矩阵[M*]和广义刚度矩阵[K*]。广义矩阵[C*]由广义质量和刚度矩阵线性组合而成。该方程可由逐步积分法求解。

将以上求解结构动力反应的方法称之为Ritz 向量法，本文简称为MRV 法。

2 算例

本文关于MRV 法是通过自编代码实现的，为验证自编代码的正确性，以商用软件ANSYS 的常规有限元法的计算结果为标准，对比自编程序的计算结果，同时对比了本文方法与常规有限元法计算量差别。

2.1 悬臂梁算例

某悬臂梁横截面尺寸为0.3m*0.5m，长2.8m，如图1所示。弹性模量为7.3E8N/m2，密度1820kg/m3，泊松比0.25。用六面体八结点等参元离散该梁，其有限元网格如图2 所示，模型共有840 个单元，1400 个自由结点，4200个自由度。

图2 有限元网格

表1 列出了悬臂梁前12 阶频率值。商用软件ANSYS给出的模态结果是采用Lanczos 法求解的，其中MRV 法取12 个Ritz 向量进行计算，从表1 可以看出，MRV 法求得的前6 阶低阶频率值有9 个以上的精确的有效数字，说明该方法自编代码正确。关于此悬臂梁的模态计算，常规有限元法需要4200 个自由度，而MRV 法仅需12 个自由度就能达到满意精度。

表1 悬臂梁前12 阶频率 单位：Hz

为进一步验证本文方法的计算精度，下面以人工地震波为激励，计算该悬臂梁梁端时程反应，并与ANSYS 计算结果对比。（图3）

图3 MRV 法和ANSYS 计算结果对比

运用MRV 法时，分4 种情况：分别取10、12、20 和30个Ritz 向量。将原系统降阶后的运动方程如式（2），其中阻尼矩阵中的质量矩阵比例系数取1.5259，刚度矩阵比例系数取0.0015。运用NewMark 法求解该运动方程时，积分系数γ 和β 分别取0.25 和0.5。计算结果列于表2。

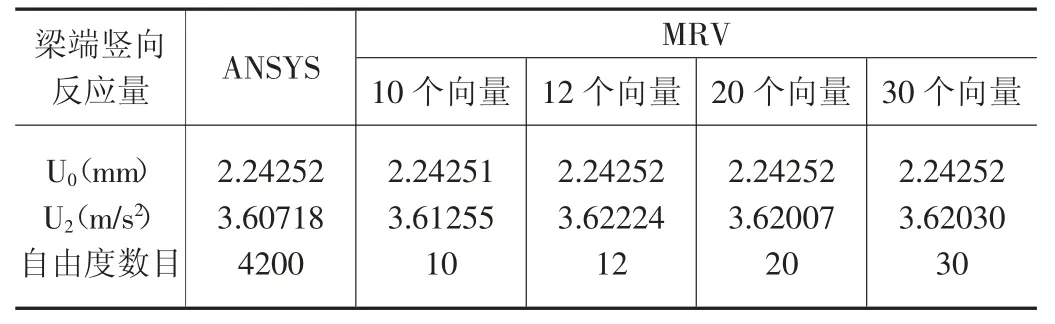
表2 MRV 法计算结果

表2 列出了悬臂梁在人工基岩波竖向激励下，梁端竖向位移与加速度的地震反应。从表中数据可以看出，MRV法计算结果与ANSYS 计算结果接近，取10 个Ritz 向量计算时，位移结果有5 个相同的有效数字；加速度结果有3个相同的有效数字，加速度误差仅为0.15%。

2.2 地下结构算例

选用双层双柱岛式地铁车站为研究对象。地面至车站顶的距离为2m，车站宽20m，高11.54m，中跨宽6m，侧跨宽6.3m，上层高3.5m，下层高6.24m。顶板、侧墙0.8m 厚，底板厚0.9m，中柱截面为0.6m×0.8m。车站横截面如图4所示。不考虑土体的非线性特性接触非线性。

图4 地铁车站标准段横截面

模型深度范围取至基岩面处，即深度取230m，水平方向长度取2320m，场地土层性质见表3。有限元网格示意图详见图5。

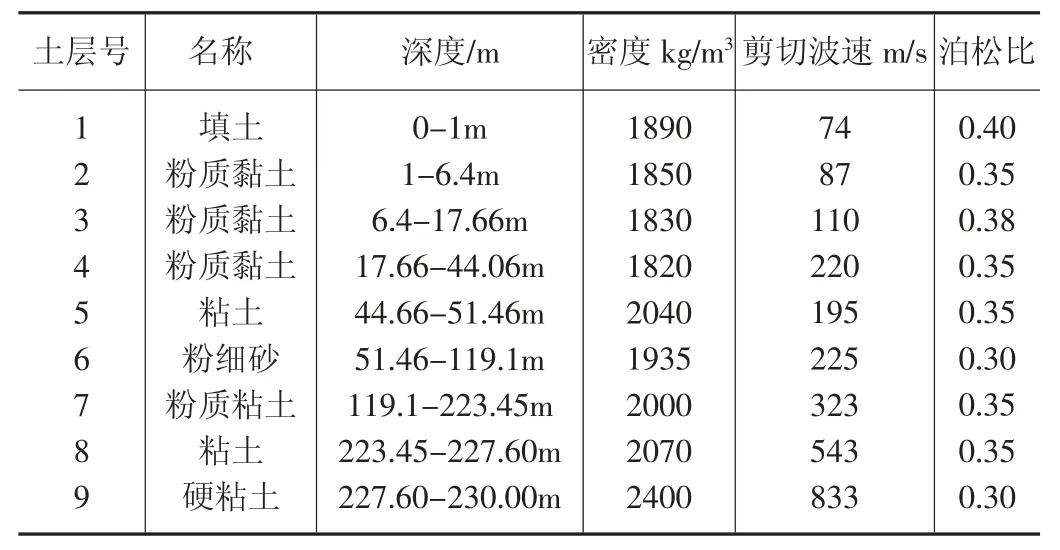
表3 场地土物理力学参数

图5 二维模型有限元网格示意图

三维模型土体部分采用八节点六面体等参元离散，中柱部分为三维梁单元离散。约束模型底部结点的所有自由度，作为地震输入激振面。选用kobe 波和汶川波作为激励，计算地下结构地震反应。为评价MRV 法的计算精度，也列出了ANSYS 的计算结果如表4。

表4 地下结构地震反应

表4 列出了在kobe 波和WC 波作用下地下结构的地震反应。从表中数据可以看出，MRV 法计算结果精度较高，相对于ANSYS 计算结果，误差最大不超过7%，但计算自由度仅为ANSYS 计算自由度的1/10 左右。这说明MRV法在地下结构地震反应分析中能极大提高计算效率。

3 结论

本文分别以悬臂梁和一地铁车站为算例，采用MRV法与ANSYS 有限元软件两种计算方法进行计算，对比了MRV 法与ANSYS 的计算结果，得出如下结论：

①采用ANSYS 软件运用Lanczos 法求解结构模态特性，常规有限元法需要4200 个自由度，然而采用MRV 法求结构模态仅需12 个自由度就能达到满意精度。

②悬臂梁在人工基岩波竖向激励下，MRV 法计算结果与ANSYS 计算结果非常接近，取10 个Ritz 向量计算时，位移结果有5 个相同的有效数字；加速度结果有3 个相同的有效数字，加速度误差仅为0.15%。

③MRV 法能有效求解大规模地下结构地震反应问题，在仅用约1%普通有限元法自由度的情况下，计算误差不超过7%。