微波湿度计条带噪声的分析与抑制方法研究

刘明绪，张升伟，何杰颖

1.中国科学院国家空间科学中心 微波遥感重点实验室,北京 100190;

2.中国科学院大学,北京 100049

1 引言

卫星气象数据的降噪一直是遥感气象数据处理领域研究的重点问题。Zou 等（2012）在处理“风云三号”A星、B星（FY-3A、FY-3B）上的微波湿度计（MWHS）和美国NOAA系列卫星上的微波湿度计（Microwave Humidity Sounder，MHS）的数据时，观测到了一种沿轨道方向随扫描角变化的直线型噪声，且噪声不可通过平均消除。因此Zou 等（2012）提出了一种通过主成分分析（PCA）与五点平滑法抑制该噪声的方法。Qin 等（2013）分析了SNPP（Suomi National Polar-orbiting Partnership）卫星上ATMS（Advanced Technology Microwave Sounder）水汽探测通道观测数据中的条带噪声，并通过主成分分析联合集合经验模态分解的方法抑制了该噪声。Li 和Liu（2016）在对MWTS-2 辐射同化的质量控制程序中引入了该条带抑制方法。对比发现，去除带噪声后分析误差小于不修正带噪声吸收数据，这表明该降噪方法的实际应用价值。Zou 等（2017）在处理ATMS 的条带噪声时，对原PCA/EEMD 方法进行了修改，避免了在海陆边界亮温急剧变化导致的降噪后的误差。同时，Zou 和Tian（2019）利用MWTS-2 扫描周期变化前后数据的差异对条带噪声进行了分析，表明噪声产生的根本原因不在于扫描速度，并给出了一种条带噪声的分析指标。金旭等（2019）通过计算噪声分布与方差，定量评估了风云三号微波温度计条带噪声的抑制效果。

目前，对于PCA/EEMD 降噪方法的各类改进、分析与应用均基于EEMD 的基础上进行。EEMD 的理论基础之一是噪声辅助数据分析NADA（Noise-Assisted Data Analysis）（Wu 和Huang，2009），因而该方法可能受到辅助噪声的影响，而导致残余噪声与虚假分量等问题。模态分解作为时频分析领域一种常见方法，已有诸多学者提出了如变分模态分解VMD（Variational Mode Decomposition）、多元经验模态分解MEMD（Multivariate Empirical Mode Decomposition）、改进的自适应噪声总体集合经验模态分解ICEEMDAN（Improved Complete Ensemble Empirical Mode Decomposition With Adaptive Noise）等变体或改进算法。其中，互补集合经验模态分解CEEMD（Complementary Ensemble Empirical Mode Decomposition）、自适应噪声总体集合经验模态分解CEEMDAN（Complete Ensemble Empirical Mode Decomposition With Adaptive Noise）及ICEEMDAN 等方法是一类试图改进并降低辅助噪声影响的方法，可有效降低重构信号后的噪声。本文通过对各类方法进行比较，试图改进原有的EEMD 方法，并应用于MWHS-2 的数据处理中。同时，本文针对风云三号微波湿度计探测数据与模态分解的特有性质，给出了一种能有效判别噪声和信号模态的新方法，可用于风云三号微波湿度计探测数据噪声特征的分析，并有助于提升分解的准确性，提升数据质量。

2 降噪算法原理

2.1 主成分分析原理

主成分分析PCA（Principal Components Analysis）是一种常见的数据分解与降维的方法。该方法基于最大化数据方差原则，将数据进行投影到低维超平面上，实现对数据的降维。Lorenz（1956）将PCA 方法引入气象数据分析领域，称为经验正交函数法EOF（Empirical Orthogonal Function）。该方法将观测数据分解为空间模态和时间系数两部分，从空间和时间域对数据进行分析（金旭等，2019）。

设MWHS观测亮温矩阵为

式中，M表示每条扫描线的视场（FOV）点，N为扫描线个数，则Tij为第j条扫描线中第i个视场的观测亮温值。

根据PCA 的原理，对亮温矩阵A的协方差矩阵AAT做特征分解，即

λi为特征值，为对应特征向量。将上式写作矩阵形式，有

E为特征向量组成矩阵，表示了使扫描线方差最大的投影方向。此外，定义

该基下，原矩阵A可表示为

表示A在第i主成分中的分量信息，称为第i模态。

2.2 模态分解原理

经验模 态分解 EMD（Empirical Mode Decomposition）是由Huang 等（1998）提出的一种针对非线性非平稳信号的自适应的时频分析方法。该方法将信号分解为若干个本征模态函数IMF（Intrinsic Mode Function），每一IMF 均包含有信号的不同时间分辨率的信息。

EMD大体步骤为

（1）根据原始信号x(t)的所有极大值极小值点，利用三次样条插值拟合出上下包络线。

（2）求上下包络线的均值m1(t)，用原信号减去该均值，得到一新序列

（3）判断中间信号h1(t)是否满足IMF 的条件，若满足，则作为第一个IMF 分量IMF1(t)，否则将h1(t)作为待分解信号，重复步骤（1）—（3），直至满足为止。

（4）用上面的方法得到第一个IMF 后，将该IMF从原始信号中分离出来，得到

（5）将r1(t)作为新的信号重复步骤（1）—（4），直到最终分解得到的rn(t)为一单调函数为止。此时分解得到的IMF1(t)，…，IMFn(t)即为所求的n个模态。

此后，为解决EMD 在处理跳变或间断时可能产生的模态混叠问题，Wu和Huang等（2009）提出了EEMD（Ensemble Empirical Mode Decomposition）方法。该方法通过在分解前添加白噪声解决了EMD 中的模态混叠问题，之后通过多次计算取平均去除白噪声的影响。

EEMD步骤如下：

已知信号为x(t)，信号中分别加入白噪声n(t)，得到

对s(t)进行EMD 分解，得到所求IMF 分量IMF1(t)，…，IMFn(t)。

重复分解m次，将每一分量所得m个IMF进行平均，最终每一IMF 分量即为m组IMF 平均的结果。

EEMD 方法虽然有效的解决了EMD 中的模态混叠，但也产生了一些新的问题。例如，在平均去噪时，由于平均次数有限，噪声不可能被完全中和，导致重构后的信号存在残余噪声。此外，由于每次添加的噪声随机，最终分解出的IMF 数量的可能会受到噪声的影响，因此平均的各IMF 并不一定对齐，而导致了虚假分量的产生。

CEEMD（Complementary Ensemble Empirical Mode Decomposition）方法（Yeh 等，2010）将EEMD 中添加的单个白噪声替换为一组符号相反的白噪声，即

s1(t)、s2(t)分别为加入正负噪声后的信号。

对s1(t)、s2(t)分别进行EMD 分解，最终将正负两组结果取平均，完成分解。该方法有效减少了EEMD分解后可能存在的残余噪声。

CEEMDAN（Complete Ensemble Empirical Mode Decomposition With Adaptive Noise）方法由Torres等（2011）在EEMD 的基础上，在EMD 计算出每个IMF 后不使用原加噪信号s(t)，而使用噪声对应IMF 分量x(t) +Ej(n(t))（Ej(·)表示EMD 分解后的第j模态）求残差，从而降低了辅助噪声的影响。同时，该方法在分解得到IMF 后立即进行平均得 到，用平均后的IMF 求残差rj(t)，即

相较于先前先求所有IMF 再平均的方法，该方法彻底避免了模态数不同难以平均的问题。

之后，Colominas等（2014）又基于CEEMDAN提出了ICEEMDAN（Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise）。先前方法提取IMF 的过程均是对信号添加噪声并进行多次迭代最终得到IMF，即

M(·)为迭代完成后移除的包络线均值总和，为均值算子。

可以看出，最终得到的IMF中包含有加噪信号和包络均值两部分平均后的残余噪声。ICEEMDAN在求IMF时使用原始信号去除包络均值

改进后的方法噪声只存在于包络均值中，去掉了原信号中的噪声，从而有效减少了最终平均后残余的噪声。此外，ICEEMDAN 对初始信号不再添加白噪声而直接使用噪声模态，从而避免了CEEMDAN中伪模式的问题。

各方法关系如图1所示。

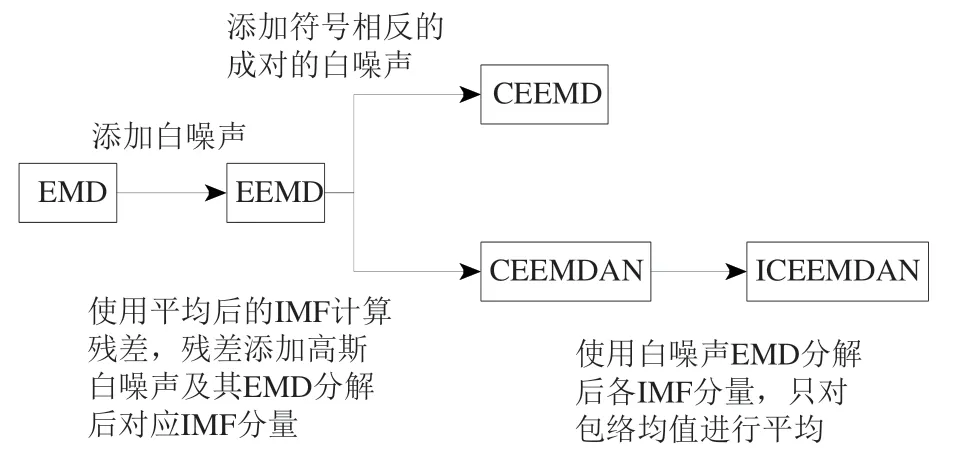
图1 模态分解算法关系Fig.1 The relationship between modal decomposition algorithms

3 降噪方法与结果分析

3.1 降噪方法

测试所用观测亮温数据选取2016 年10 月8 日与2019 年1 月10 日湿度计采集的各14 组亮温数据进行测试。其中，118.75 GHz 附近的第4 通道（118.75±0.3 GHz）有较为明显的条带噪声。模拟亮温数据由对应时间的ERA5每小时全球再分析分层网格数据与ERA5-land每小时地面网格数据导入RTTOV-SCATT 模块仿真生成。网格分辨率0.25°×0.25°，气压层选取50 hPa—1000 hPa间共29层。

部分区域的观测亮温如图2（a）所示。可以看出，亮温图像中有明显的扫描线方向的条纹状噪声。

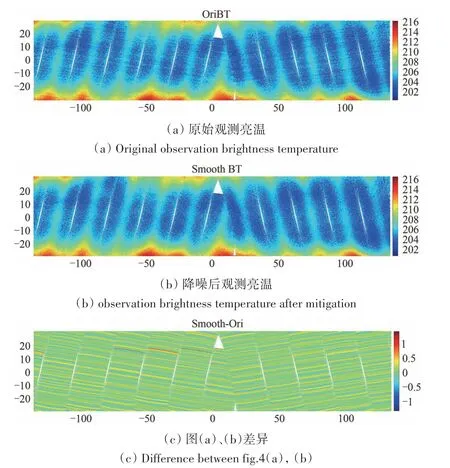
图2 条带噪声去除前后亮温图及（a）、（b）间差异Fig.2 Brightness temperature before and after removing the striping noise and difference between（a）and（b）

对数据进行PCA 分解，得到其各个PC 分量（图3），可以看出第一PC 模态中有明显的水平条纹。根据PCA 的原理，第一主成分方向为信号差异最大的方向，而观测亮温中的差异主要来源于卫星轨迹方向宏观的天气变化，因此第一主成分分量包含了最多的沿卫星轨迹方向包括条带噪声在内的天气信息。通过计算方差贡献率

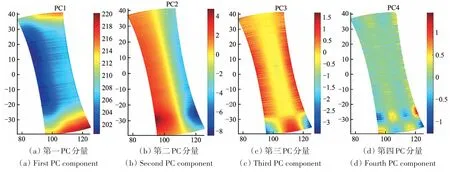
图3 第1—4 PC模态空间分布图Fig.3 Spatial distribution of 1-4 PC modes

第一主成分方差贡献比例超过99.98%，表明绝大部分的沿轨方向数据差异都成功保留在了第一主成分分量中。后续模态包含了沿扫描线变化及各类小尺度波动信息。因此，仅对进行模态分解，也可较为准确且高效的提取出绝大部分条带噪声，且可有效降低处理的数据量，提高计算效率。

分解后所得前7 个IMF 如图4。可以看出，前几个IMF主要包含了信号中的高频噪声，后续模态保留了各类天气信息。分解后的PC分量可表示为

IMFn和IMFs分别为噪声主导和信号主导的IMF分量，r(t)为提取完所有IMF后的直流分量。

因此，只需选择合适的划分位置，分离出噪声主导的前几个IMF分量并去除，即可得到重构信号

定义信号能量密度为

式中，N为IMF 长度，IMFj(i)表示第j个IMF 序列的第i个元素。

由于IMF 极值点与零点相同（或差一）的定义，IMF可近似看作一周期振荡的函数。因此，可利用其极值点个数nl定义IMF 的平均周期T（Wu和Huang，2004）

同时，Wu 和Huang（2004）指出，对于白噪声，IMF函数S(lnT，j)在对数坐标下积分后的数值相同（c为常数）。

该式等价于

对于本文所述条带噪声，虽无法证明其为白噪声，但观察各IMF的频谱（图5）可以看出，前5个IMF 峰值明显低于后续IMF，且除包含残余噪声的第一IMF外，其余几个IMF具有相似的波形，这与Wu和Huang（2009）的实验结果近似。因此，不妨尝试计算各IMF能量密度与平均周期的乘积EnTn并计算相邻IMF间能量之比。在噪声IMF之间，该比值较小，而在噪声与信号间，比值会突变。可寻找出比值变化最大的间隔作为信号与噪声的划分P：

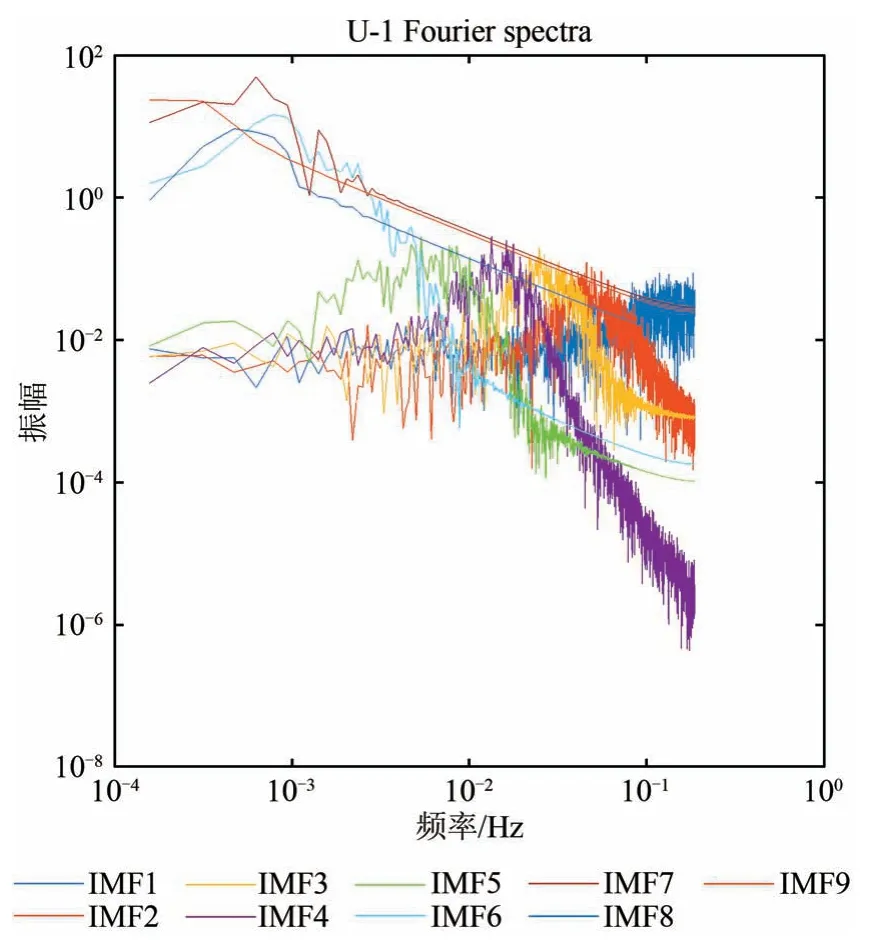
图5 第一PC分量IMF1-10频谱图Fig.5 Fourier spectra of the first PC coefficient IMF1-10

同时，为避免对无噪声通道的误处理，在寻找出最大比值后还需对其进行约束。比较有噪声通道和无噪声通道的频谱发现，无噪声通道并无明显的能量突变。因此可定义仅当最大突变超过某一阈值时才将其定义为噪声并进行划分。对于本文，阈值定义为0.8，实际操作过程中，可以实现较好的划分效果。

在模态分解方法的选取上，如2.2 节所述，EEMD 会因残余噪声和虚假分量而在重构后产生误差，使得天气信号分量受到噪声的影响。同时，EEMD平均时模态数不一定对齐，致使分解后的直流分量也混杂到了IMF 中，使噪声选取方法失效。因此本文采用了ICEEMDAN 方法进行处理，并最后重构出亮温信号

3.2 结果分析

降噪前后的亮温图像及提取出的噪声如图4（b）（c）。可以看出，算法成功提取出了信号中的条带噪声并重构出了观测亮温。对比图6可以看出，重构后的信号O-B 亮温并无明显偏移与失真，该方法恢复后的数据中保留了信号中绝大多数的亮温信息。其中单独提取出第49 视场角并去除前n个IMF后绘制的亮温曲线如图7。可以看出，随着去除的IMF 数增加，信号逐渐趋于平滑，且各级模态分解均主要抑制的是信号中的高频振动，对信号整体趋势变化并无太大影响。同时，对提取出的噪声进行统计，其概率分布（图8）整体呈现出近似于无偏的高斯噪声的分布特征。

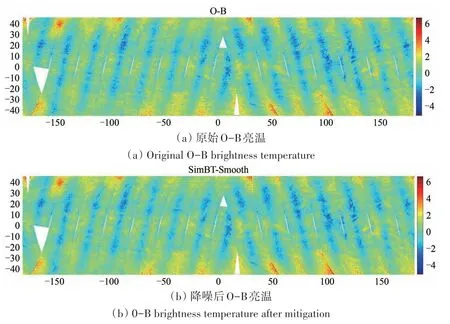
图6 噪声抑制前后O-B亮温图Fig.6 O-B before and after removing the striping noise

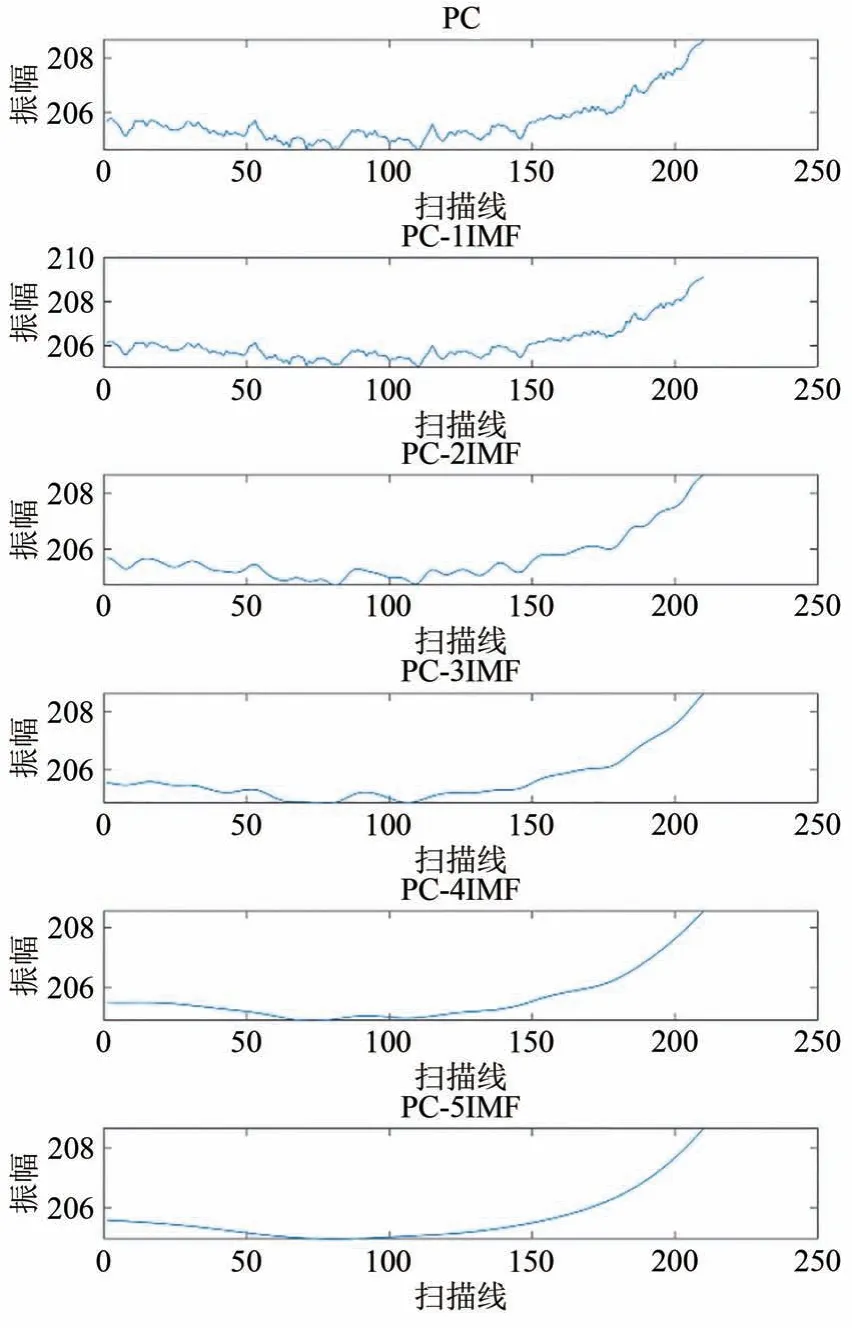
图7 去除前1—5 IMF后重构出的第49视场角亮温随扫描线变化图Fig.7 Reconstruction of the 49th FOV brightness temperature changes with the scan line after remove the first 1—5 IMF

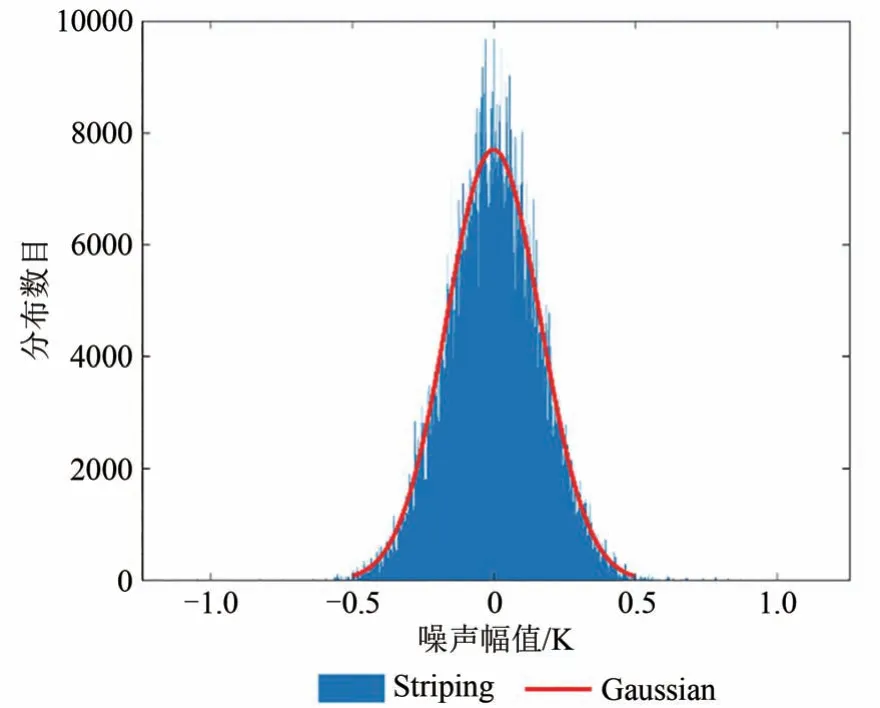
图8 条带噪声概率分布直方图Fig.8 Histogram of probability distribution of striping noise

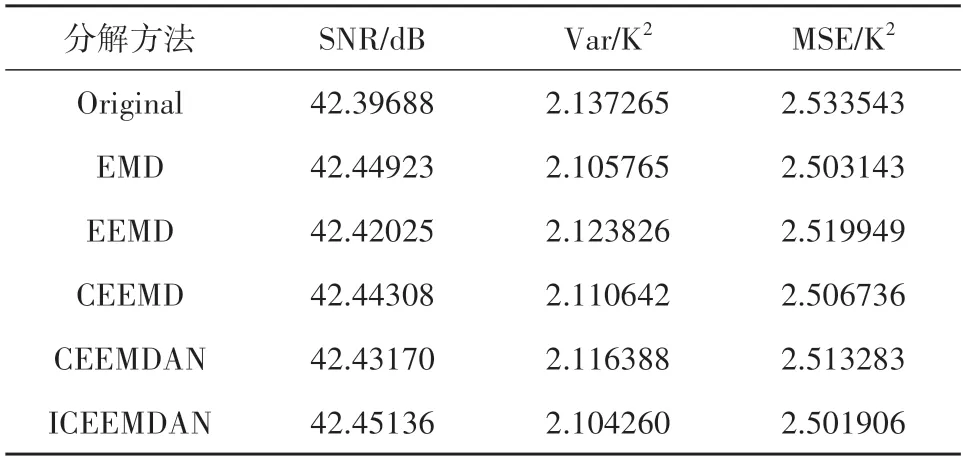
表1 各模态分解方法降噪效果Table 1 Mitigation effect of each modal decomposition method

可以看出，各类方法相较于原始信号均在不同程度上对噪声进行了抑制。信噪比越高效果越好，方差和均方误差相对越低越好。对比各类方法，可以看出相较于原始的EEMD 算法，改进后的CEEMD 等方法在去噪效果上均有不同程度的提高。其中ICEEMDAN 在各方面效果最好。相较于EEMD，该方法使信噪比提高了0.031 dB，方差降低0.020 K2。且多次实验表明该方法具有较好的稳定性，有助于提高算法的噪声抑制效果。

4 结论

本文主要介绍了针对MWHS-2 中的条带噪声的一种有效的降噪方法，并给出了改进方案。本文首先使用主成分分析对数据进行了降维，随后通过模态分解将信号分解包含噪声和天气信息的不同IMF分量，利用两类IMF在能量密度上的差异进行自动划分，重构剩余模态，实现了噪声的抑制。针对EEMD 残余噪声等问题，本文采用ICEEMDAN 进行PC 分量的分解、降噪与重构操作。在对MHWS-2 数据的处理过程中，证明了该方法的有效性。同时，本文针对各种不同的模态分解方法的降噪效果进行了统计与对比，数据结果表明，各类改进方法均可在不同程度上实现噪声的抑制。其中，使用ICEEMDAN 进行模态分解降噪并恢复后的数据使信噪比提高了0.054 dB，方差降低0.032 K2，具有良好的重建效果，可使重构后的数据精度得到进一步提高。

模态分解是经验上近似的二进滤波器，即以相邻模态间周期大致为2 倍的关系对信号进行分解，并不一定能将噪声和信号准确的划分开。直接对模态进行删除只能滤除绝大多数噪声，并不能保证剩余模态中没有噪声残余。同时，本文以能量差异进行划分的方法，只针对所用微波湿度计数据进行了测试，仅作为一种思路以供参考，对于其适用范围的普遍性和对各类数据划分的稳定性，还有待进一步的探索。

志 谢文中所用湿度计相关数据来自国家卫星气象中心，在此表示衷心的感谢。