基于启发式算法的应急物资储备点选址模型研究

裴姝艺，叶晓飞，洪 钢，周义雄，郑彭军

（1.宁波大学 海运学院，浙江 宁波 315211；2.宁波中通物流集团有限公司，浙江 宁波 315211）

0 引 言

随着世界经济的快速发展和科学技术的进步，重大突发事件的数量、经济损失的数量和受灾人口的百分比显著增加。在紧急情况下，人们需要应急医疗援助和应急物资，因此需要尽快将这些资源和救援人员从救援中心运送到受影响地区。在此情况下，如何设计和选择应急物资储备点作为关键的应急物资配送节点就成为一个备受关注的问题，具有宝贵的理论意义和应用价值。

应急物资储备点选址问题涉及如何选择潜在储备点的选址，以及如何通过储备点运输产品，从而将总相关成本降至最低。目前已经有许多学者提出了几种经典算法来实现该问题，可分为定性方法和定量方法两类。定性方法包括层次分析法[1]、专家选择[2]、比较分析法[3]和模糊评价[4]。这些方法可以解决部分选址问题，但也包含着一些主观因素。定量方法包括重力法[5]、混合整数规划[6]、双层规划[7]和鲁棒优化算法[8]。

但是，当问题规模较大时，鉴于NP难（多项式复杂程度的非确定性问题）的性质，解决问题变得更加困难，线性规划方法已经较难满足现实需要。由于精确技术有限，人们已经投入了相当多的精力来开发有效的元启发式算法（或混合元启发式算法），这些算法可以为大规模问题提供近乎最优的解决方案，如粒子群算法[9]、禁忌搜索算法，模拟退火算法、可变邻域搜索、帝国主义竞争算法和遗传算法等。

本文为更好地解决应急物资储备点选址问题，构建了数学模型，尽可能降低建造、储备和调运成本，并考虑储备点最大容量的限制。同时本文求解采用启发式模拟退火算法和启发式遗传算法，并对两种方法进行比较，得出较优方法。从而得出的最优成本与精确解进行比较，来判断算法所得解的可靠性，并对比两个算法的运算速度和收敛情况。

1 应急物资储备点选址考虑因素

应急物资储备点模型通常以系统总成本最低为目标函数，建立模型时主要应对以下四项费用进行考虑。

1.1 应急物资储备点建设成本

应急物资储备点建设成本包括建筑物、设备和土地征用等费用，与应急物资储备点的位置和规模有关。

1.2 应急物资储备点经营成本

经营费用是应急物资储备点在经营过程中发生的费用，如物资储备费用、进出库费、保管维护费等，与应急物资储备点的经营规模有关。

1.3 调运成本

调运成本是应急物资运输过程中所产生的费用，主要包括运价、物资运送折损费用等，与应急物资储备点的位置有关。

1.4 其他成本

应急物资储备点的员工工资、固定资产折旧等费用。

为了将问题简化，本文仅考虑建造投资成本、物资储备成本和物资调运成本。

2 建模与分析

2.1 模型的建立

本模型假设已有n个应急物资储备可选点，从中选择q个作为新建物资储备点，并确定储备点的储备量。新建物资储备点的总建设存储费用和最大容量有限制（作为约束条件）。目标是在满足应急物资需求量（作为约束条件）的前提下，尽可能降低建造、储备和调运成本。

可选择新建应急物资储备点的点集合S={si|i=1，2，...，q，...，n}。应急物资需求点集合为F={Fj|j=1，2，...，m}。

为了不断优化和完善数值模式的中小尺度预报能力,需要对微物理参数化方案进行对比研究,以便找到影响某一区域强降水过程预报能力的主要微物理过程。因此本文利用中尺度WRF数值模式,分别采用Morrison和Milbrandt-Yau双参微物理方案对辽宁省的一次强降水过程进行数值模拟,通过对地表累积降水量、降水强度和云中微物理量以及微物理过程的分析,对比研究了以上两种双参云微物理方案对强降水的预报效果,并找到降水预报差异的具体云微物理过程。

2.1.1 构建目标函数

zi为物资储备点i的储备物资量，i=1，2，...，q，...，n；

cbi为物资储备点i的建设成本，i=1，2，...，q，...，n；

cs为物资储备点的仓储成本，统一为2万元/万件；

ct为运输成本，统一为0.012 5万元/万件*公里；

aij为物资储备点i向需求点j提供的物资数量，i=1，2，...，q，...，n；j=1，2，...，m；

dij为物资储备点i到需求点j的最短距离，i=1，2，...，q，...，n；j=1，2，...，m。

如果物资储备点i未被选中，则该点无储备量，也不向需求点提供物资，即：

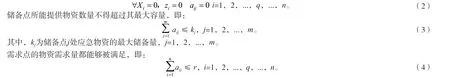
其中，r为全部需求点对应急物资的需求总量。

非负约束，Xi为0—1变量，其他所有变量≥0。

2.2 模型的求解

根据需求点的需求量、点i到点j的运输距离、单位运输成本以及储备点的建设和仓储成本等条件，按照2.1中构建的模型求解应急物资储备点最优的位置与储备量。

求解采用启发式模拟退火算法和启发式遗传算法。

2.2.1 模拟退火算法

模拟退火算法（Simulated Annealing，SA）是一种模拟金属缓慢冷却的优化方法，其特征是原子运动逐渐减少，从而降低晶格缺陷的密度，直至达到最低能量状态。以类似的方式，在每个虚拟退火温度下，模拟退火算法根据预定义的标准，通过改变当前状态来为所考虑的问题生成新的潜在解决方案。然后，新状态基于预定义的标准判断是否保留，并且此过程迭代直到收敛。

根据应急物资储备点选址模型，本文算法的参数分别为：外层迭代次数为2 000次，内层迭代次数为350次，初始温度为100℃，温度衰减系数为0.99。

模拟退火算法首先随机生成一个初始解决方案，从中探索该初始解决方案的周围环境，接受更好的解决方案并以某种概率接受较差的解决方案。为了避免出现局部最小值的情况，搜索方向不一定朝向更好；当温度较高时，得到优解或差解的概率相对较高，这使得算法能够进行全局搜索。随着温度的降低，接收到更高级的溶液，并且接收较差解决方案的概率变得很低，因此它逐渐收敛到最佳状态。

模拟退火算法包含两个迭代循环，即退火过程的冷却过程和Metropolis准则。根据Metropolis准则，粒子在温度T时趋于平衡的概率为exp(-ΔE/T)，其中E为温度T时的内能，ΔE为其改变量。用固体退火模拟组合优化问题，将内能E模拟为目标函数值，温度演化成控制参数。从某个初始解出发，经过大量解的变换后，可以求得给定控制参数值时组合优化问题的相对最优解。然后减小控制参数的值，重复执行Metropolis算法，就可以在控制参数趋于零时，最终求得组合优化问题的整体最优解。模拟退火算法的流程如图1所示。

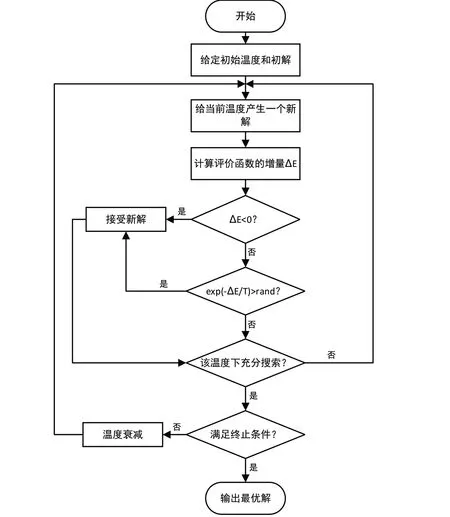
图1 模拟退火算法流程图

2.2.2 遗传算法

遗传算法（Genetic Algorithm，GA）是根据生物进化特性提出的一种算法，根据基因序列组合特性生成新解。

根据应急物资储备点选址模型，本文算法的参数分别为：种群规模为50，最大迭代次数为2 000次，选择策略为轮盘赌法，交叉概率为0.5，变异概率为0.4。

遗传算法是随机搜索算法，旨在模仿自然选择和自然遗传学的机制。遗传算法在字符串结构上运行，例如生物结构，这些结构通过使用随机但结构化的信息交换，遵循适者生存规则在时间上进化。遗传算法的主要步骤包括选择、交叉和变异。选择操作从种群中根据一定概率选出优良个体组成新的种群，以繁殖得到下一代个体，个体被选中的概率与适应度值成正相关。本文选择采用轮盘赌选择法，也叫适应度比例法，依据个体的适应度值计算每个个体在子代中出现的概率，并按照此概率随机选择个体构成子代种群。交叉操作是指从种群中随机选择两个个体，通过两个染色体的交叉互换组合，把父串的优秀特征遗传给子串，从而产生新的优秀个体。变异操作是指在种群中随机选择个体，基于变异概率对个体进行变异。遗传算法的流程如图2所示。

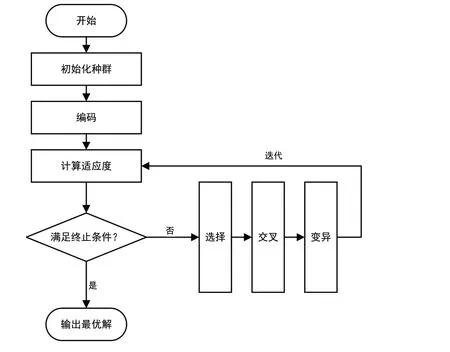
图2 遗传算法流程图

3 案例介绍

本文算例以四川省作为分析对象。设定应急物资需求点共15个，包括汶川、绵竹、北川等地。拟定应急物资储备点备选点有4个，包括成都、绵阳等地，从中选择数个作为新建物资储备点。需求点及储备点地理位置如图3所示。

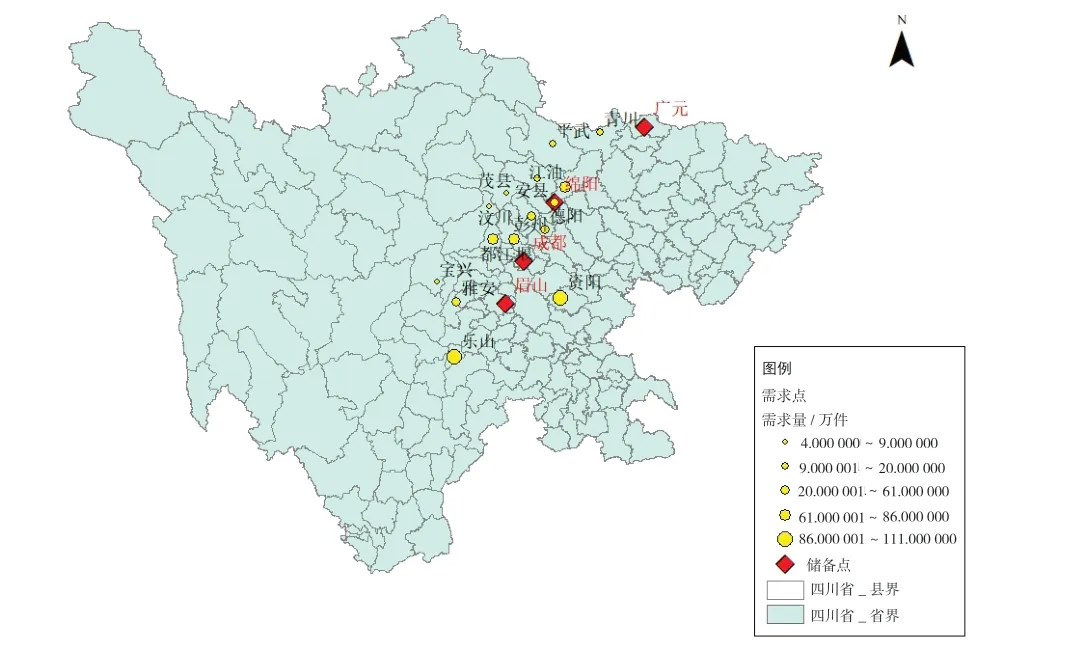
图3 需求点及储备点地理位置图

应急物流中心的建设成本、各区域的应急物资需求量以及与备选点的对应距离[8]分别如下表1、表2和表3所示，各地点的经纬度参考腾讯地图。

表1 应急物流中心备选点建设成本

表2 需求点应急物资需求

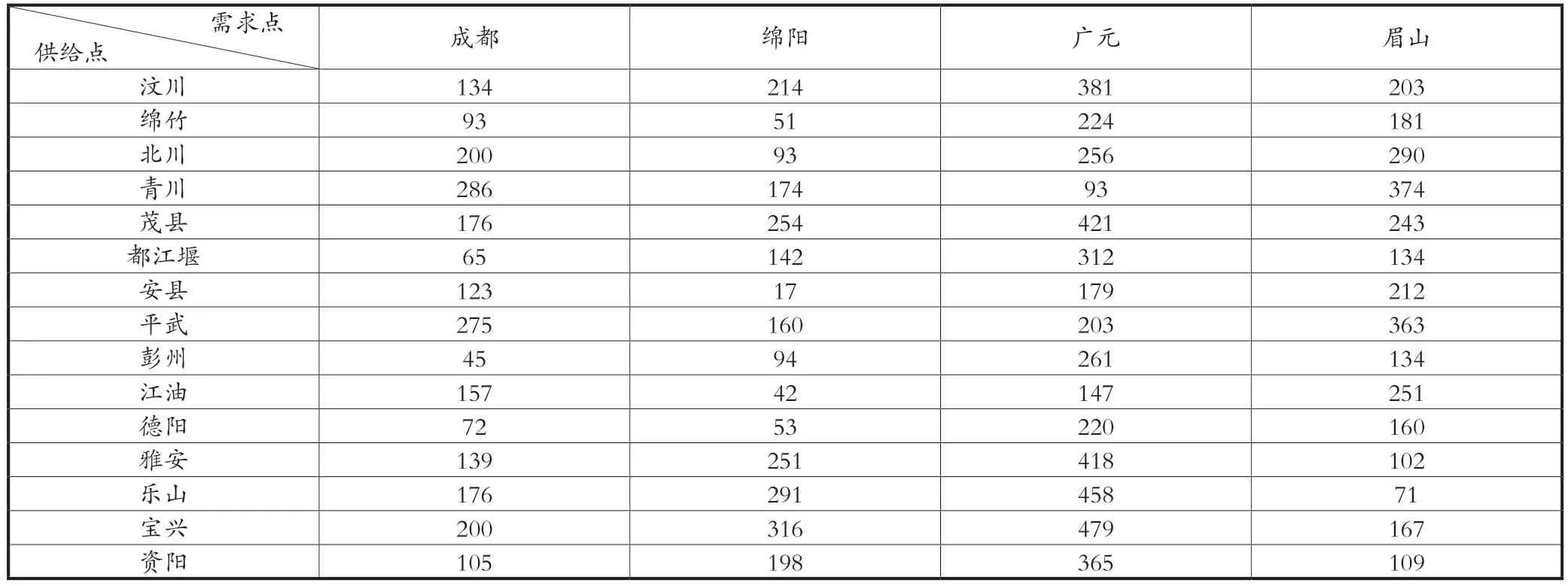
表3 需求点与应急物流中心备选点距离

4 结果对比分析

本文使用较小规模的案例，故而线性规划方法可行，以便求得精确的成本最小解，并以此来判断两种启发式算法求解的正确程度。

根据计算，精确解为2 849.237 5万元。选取的应急物资储备点为成都、绵阳、眉山。其中，成都储备点对应的需求点为汶川、茂县、都江堰、彭州、资阳，总物资数为271万件；绵阳储备点对应的需求点为绵竹、北川、青川、安县、平武、江油、德阳，总物资数为292万件；眉山储备点对应的需求点为雅安、乐山、宝兴，总物资数为176万件。对应连接图如图4所示。

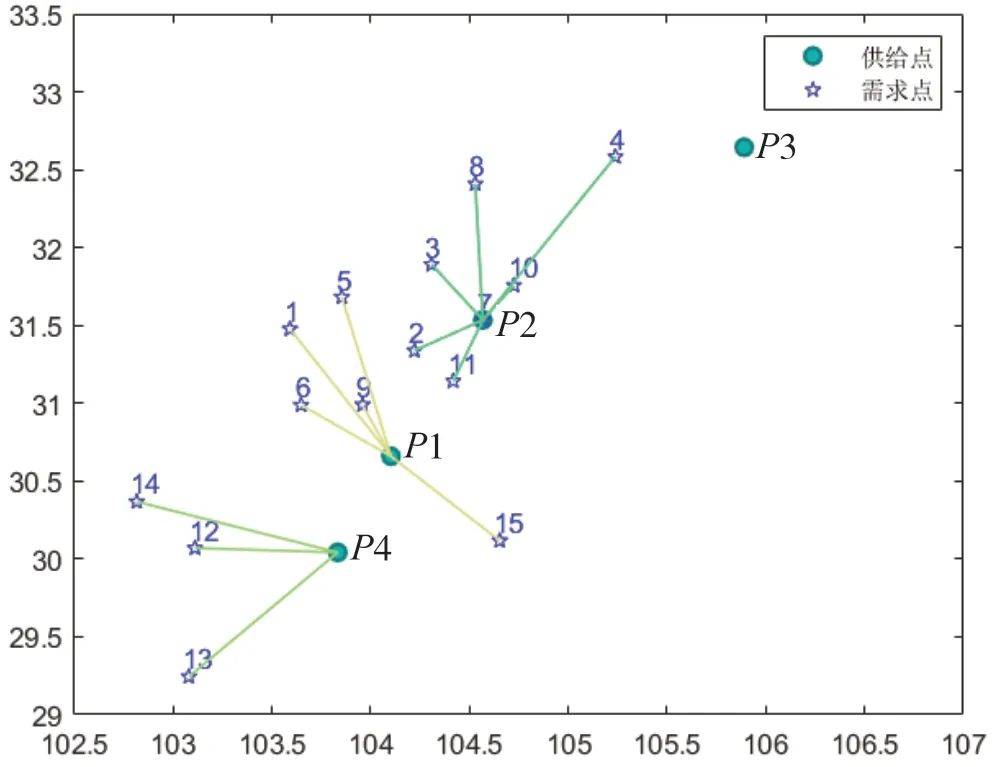
图4 应急物资储备点与对应需求点连接图

本文使用模拟退火算法和遗传算法各运行4次，得出最优成本、运行时间及收敛情况，分别如图5、图6所示。

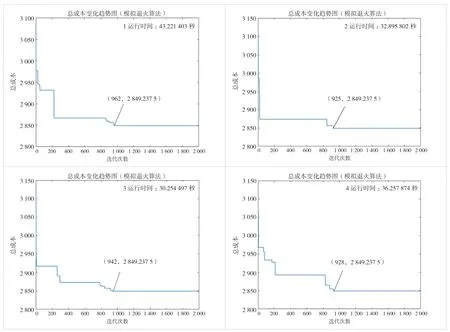
图5 模拟退火算法最终解及收敛程度图

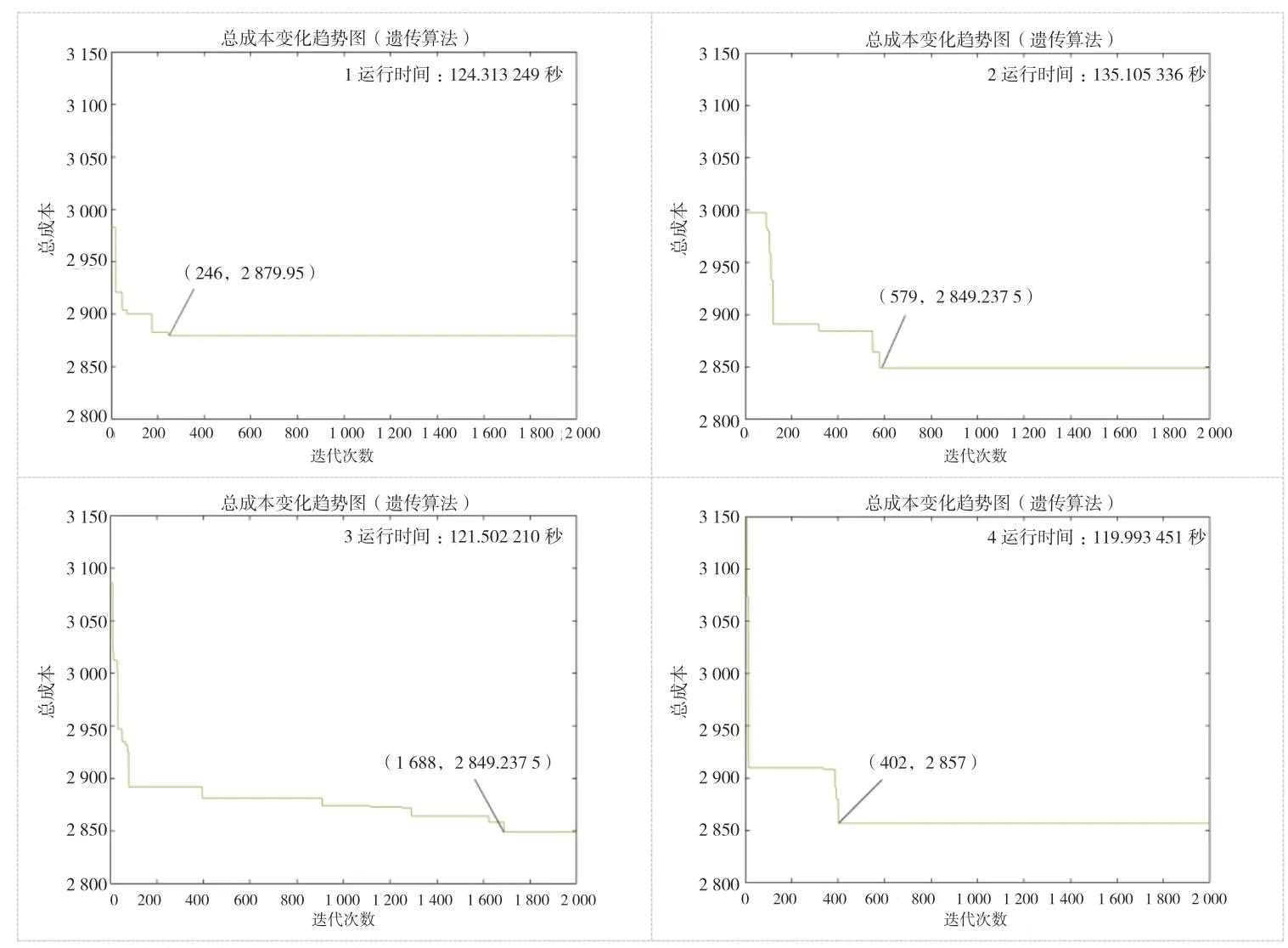
图6 遗传算法最终解及收敛程度图

由图5、图6可知，模拟退火算法所得解更精确，4次运算的最优成本皆为2 849.237 5万元，与前文所得精确解一致，可得该算法所得解可靠性较高。4次运算运行时间平均为35秒左右，且都稳定在迭代900多次后收敛。

而遗传算法4次运算只有2次最优成本符合精确解，且所得解局部最优缺陷较为明显。并且运行时间平均为124秒左右，收敛规律也不明显、变动较大。

因此，本研究结果表明，模拟退火算法与遗传算法相比，其求得全局最优解的正确率更高，运算速度更快、收敛情况更稳定。

5 结 论

本文在考虑建设、储备和调度成本最小化的基础上，建立了应急物资储备点选址模型，同时还设定了储备点最大容量约束，使其更符合实际情景。并对四川省进行了算例分析，验证了所提方法的有效性。求解分别采用启发式模拟退火算法和遗传算法，在多次迭代下选取最小成本结果。并在精确解的参考下，判断了两种启发式算法所得最终解的正确情况、运行速度和收敛情况。实验结果表明：由最小成本化模型得到的最优成本为2 849.237 5万元；遗传算法容易陷入局部最优问题，而模拟退火算法求得全局最优解的可靠性较高、运行速度较快、收敛情况也更稳定。