高能量电子激发比压阿尔芬本征模的全域模拟研究*

包健 张文禄 李定

(中国科学院物理研究所,软物质物理实验室,北京 100190)

采用自主开发的本征值程序MAS,基于朗道流体-漂移动理学混合物理模型,针对近期实验上观测到的高能量电子激发比压阿尔芬本征模(e-BAE)开展动理学模拟研究.通过在全域环几何位形下非微扰求解e-BAE色散关系,得到了e-BAE 实频率、增长率和模结构随环向模数的变化特征,并发现e-BAE 在高能量电子密度-温度参数空间下存在不稳定岛,而在传统微扰理论下则不存在不稳定岛.进一步分析了高能量电子非微扰效应对e-BAE 模结构对称性破缺的影响,结果表明: 增大高能量电子温度可以引起显著的极向对称性破缺;移动高能量电子密度剖面使其驱动强度关于有理面不对称时,e-BAE 模结构产生径向对称性破缺,并且扰动幅度在平行波数谱空间下分布不对称,从而引起等离子体自发旋转.本文研究结果为理解实验上e-BAE 的激发与传播特征具有参考意义.

1 引言

随着托卡马克上中性束和射频波加热功率的提升,大量高能量粒子(energetic particles,EP)会在辅助加热过程中产生[1],不同能量和投掷角的EP 可以通过波-粒子共振激发各类阿尔芬本征模[2,3],进一步造成EP 输运和等离子体约束水平下降[4].近期,我国HL-2A 装置上电子回旋波加热实验首次证实了高能量电子可以激发比压阿尔芬本征模(energetic electron driven beta-induced Alfvén eigenmode,e-BAE)[5],EAST 装置在相似实验条件下也观测到类似e-BAE 的磁流体不稳定性[6],由于高能量电子的归一化轨道及特征频率与未来聚变堆等离子体中的α 粒子相接近,理解高能量电子激发低频磁流体不稳定性对研究α 粒子物理具有重要借鉴意义[7].

针对e-BAE 的激发机制和饱和机制已开展了一系列理论和初始值模拟研究,发现深度捕获高能量电子通过进动共振激发e-BAE[8-11],并且共振高能量电子的非线性响应对e-BAE 产生带状流具有重要贡献[12].然而,由于不同研究手段的局限性,e-BAE 的线性性质尚未被完全理解.例如理论上采用气球模表象求解e-BAE 色散关系,其要求平衡剖面和模结构具有较大的尺度分离[13],无法准确描述低环向模数的情况;而初始值模拟采用粒子-网格方法,包含高能量电子的动理学效应,一方面时空步长受到真实电子质量的严格约束[14],另一方面需要模拟大量粒子降低数值噪声,由于计算量大难以在参数空间中进行大量扫描.

本征值模拟是研究e-BAE 线性物理性质的有效方法,一方面将物理方程在托卡马克全域环几何位形下离散并转换为矩阵本征值问题进行求解,不依赖于空间尺度分离假设;另一方面对时间进行傅里叶变换,无需在时域上演化物理量,极大节省了计算量.基于朗道流体物理模型的MAS 本征值程序可以包含主等离子体的动理学效应,已被用于分析常见的阿尔芬本征模,包括环形阿尔芬本征模、反磁剪切阿尔芬本征模和比压阿尔芬本征模等[15-17].近期MAS 程序中加入了高能量电子物理,通过求解漂移动理学方程得到扰动分布函数,包含重要的动理学非绝热响应和流体对流响应,并且经过与第一性原理粒子-网格程序GTC 校验,MAS 程序可以准确计算e-BAE 的模结构和色散关系.围绕目前实验上重点关注的高能量电子激发e-BAE 温度/密度阈值及模结构对称性破缺两个重要问题,本文采用MAS 程序在参数空间下开展e-BAE 的动理学模拟研究.

本文第2 节介绍模拟采用的朗道流体-漂移动理学混合物理模型;第3 节分析了e-BAE 实频率和增长率对环向模数、高能量电子温度和密度的依赖关系,以及高能量电子非微扰效应引起的e-BAE模结构对称性破缺;第4 节是总结和讨论.

2 物理模型

MAS 程序采用朗道流体模型描述主等离子体,漂移动理学模型描述高能量电子,二者构成一个非微扰的混合物理模型,自洽包含主等离子体抗磁漂移、朗道阻尼、有限拉莫尔半径,以及捕获高能量电子进动共振等重要动理学效应.MAS 程序求解的方程组包括涡量方程、平行方向欧姆定律、离子压强方程、平行方向动量方程和离子连续性方程,具体形式依次为[15,16]

电子扰动密度 δne和电子平行方向扰动速度 δu//e分别通过准电中性条件和平行方向安培定律进行求解:

高能量电子扰动密度 δnh、平行方向扰动速度 δu//h和扰动压强 δPh由其扰动分布函数在速度空间积分得出,并且通过(1)式、(9)式和(10)式与主等离子体朗道流体模型进行耦合,具体形式是

3 模拟结果

3.1 平衡参数

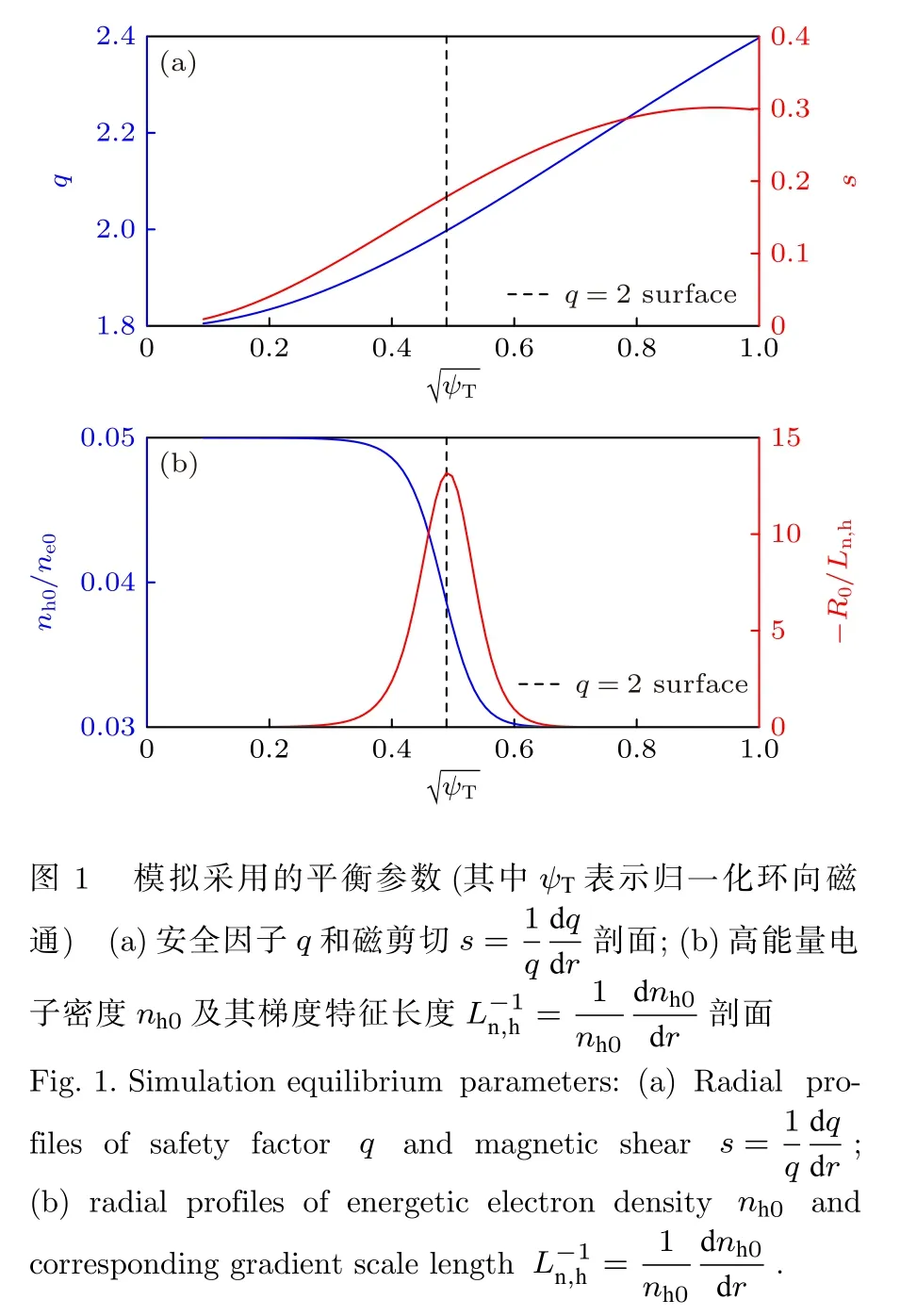
为了分析e-BAE 的主要物理特点,本文采用文献 [10]中的同心圆截面解析平衡参数进行计算,具体包括: 磁轴处磁场强度大小B0=1.91 T、大半径R0=0.65 m、小半径a=0.333R0,安全因子q和磁剪切s=(1/q)(dq/dr) 剖面如图1(a)所示.采用质子为主离子(电荷为Zi=e),主离子和主电子、高能量电子温度均匀分布,分别为Ti0=Te0=500 eV和Th0=25Te0.主电子密度均匀分布ne0=1.3×1014cm-3,高能量电子密度nh0剖面如图1(b)所示.在q=2 有理面处驱动强度最大|R0/Ln,h|max=12.7,其中Ln,h=(∇nh0/nh0)-1为梯度特征长度,主离子密度ni0则由准电中性条件Zini0+qe(ne0+nh0)=0确定.

3.2 阿尔芬连续谱与e-BAE 特征

首先在不同环向模数n下,计算理想磁流体连续谱和e-BAE 本征模,如图2 所示.在q=2 有理面附近,m=nq的极向分量形成连续谱势阱,其最低极值点是BAE 连续谱积累点(continuum accumulation point,CAP)[18],并且BAE-CAP 的频率不随n变化.结合图2 和图3 可以发现,在n=2增大到n=5 的过程中,连续谱势阱逐渐变窄,由于BAE 本征模是动理学阿尔芬波束缚在连续谱势阱内形成的[19],因此e-BAE 模结构的径向宽度也相应变窄.在图3(a1)—(d1)中,e-BAE 静电势δφ的二维模结构呈现“回旋镖”形状,这是由高能量电子非微扰效应造成的: 即(15)式代入(1)式后,涡量方程(1)包含反厄米分量贡献,引起e-BAE 极向模结构具有上-下不对称性,这与近期e-BAE 的气球模理论研究结论相似[9],并且在高能量离子激发BAE 的理论和模拟研究中也观察到对称性破缺现象[20,21];另一方面,如图3(a2)—(d2)所示,e-BAE 由一个主极向分量和两个边带极向分量组成,主极向分量在q=2 有理面处满足共振条件m=nq且幅度远大于边带极向分量,因此e-BAE 呈现弱气球模结构.

图2 (a)—(d)环向模 数 n=2,n=3,n=4和n=5 的连续谱,其中细线代表声波,粗线代表阿尔芬波,彩色代表归一化的e-BAE 振幅强弱;纵轴刻度单位是 VA0/R0 (即 磁轴处阿尔芬频率),其中 VA0=B0,a/ 为磁轴处阿尔芬速度,R0 为 磁轴处大半径,B0,a 为磁轴处磁场,ni0,a 为磁轴处离子密度Fig.2.(a)-(d) Continuous spectra of toroidal mode numbers n=2,n=3,n=4 and n=5,where the thin line represents the acoustic branch,the thick line represents the Alfvénic branch,and the colorbar represents the normalized radial amplitude of e-BAE.

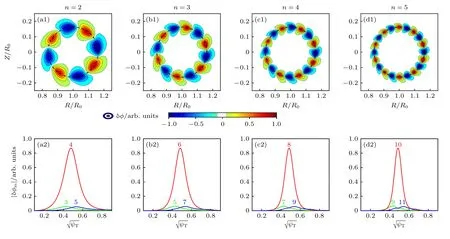
图3 (a1)—(d1)环向模数 n=2,n=3,n=4和n=5 的e-BAE 静电势 δφ 二维模结构;(a2)—(d2)各极向傅里叶分量剖面Fig.3.(a1)-(d1)The 2D poloidal mode structures of electrostatic potential δφ of toroidal mode numbers n=2,n=3,n=4 and n=5;(a2)-(d2) radial profiles of each poloidal harmonics.

进一步分析e-BAE 色散关系: 实频率主要是由BAE-CAP 决定的,几乎不随n变化,如图4 蓝线所示.尽管高能量电子抗磁漂移频率ω∗n,h和ω*T,h与n成正比,自由能在高n时更容易释放,但由于捕获高能量电子通过进动共振驱动e-BAE,因此共振条件匹配度ζ=ω/ωD0与n成反比,最终使得e-BAE 增长率随n先增大后降低,如图4 红线所示.

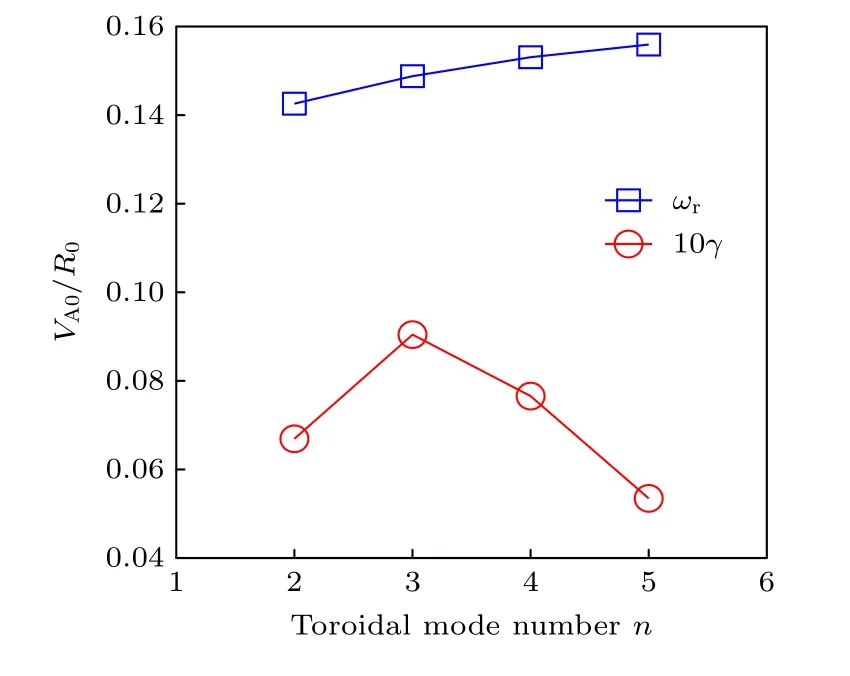
图4 e-BAE 实频率和增长率随环向模数 n 的变化,其中纵轴刻度单位是 VA0/R0 (即磁轴处阿尔芬频率)Fig.4.The e-BAE real frequency and growth rate dependences on the toroidal mode number n.

3.3 高能量电子温度和密度对e-BAE 色散关系的影响

传统研究通常采用微扰方法计算高能量粒子激发阿尔芬本征模,即求解主等离子体方程计算阿尔芬本征模实频率和模结构,再代入到EP 贡献项中计算增长率[22].随着实验上加热功率的提高,EP 与主等离子体的比压已经接近,实验和第一性原理模拟研究均表明EP 对阿尔芬本征模实频率和模结构的非微扰效应不可忽略[23-25].为了更加符合当前EP 实验情况,MAS 程序采用非微扰模拟方法,自洽包含高能量电子贡献项对模结构、实频率和增长率的影响.这里选取图4 中最不稳定的n=3 e-BAE,计算实频率和增长率在nh0,a-Th0参数空间中的分布,这里nh0,a代表磁轴处的高能量电子密度值,另外本文模拟中高能量电子温度分布均匀,因此采用Th0代表其温度值.如图5(a)所示,实频率ωr随着nh0,a和Th0增大而降低,这是由于方程(14)代入(1)式后磁流体交换模项增大造成的[18];另一方面,由于ωr随nh0,a的变化影响了共振条件匹配度ζ=ω/ωD0,因此增长率γ不再随nh0,a单调增大,而是随nh0,a先增大后降低,形成图5(b)中的不稳定岛;另外MAS 模拟同时包含高能量电子驱动效应和背景等离子体阻尼效应,只有对于图5(b)中青蓝色实线(γ=0)边界内的nh0,a和Th0参数区 间,e-BAE 才可以不稳定,激发e-BAE 的最低高能量电子比压 min(βh,crit) 对应的nh0,a和Th0如图5(b)中红色五角星所示.

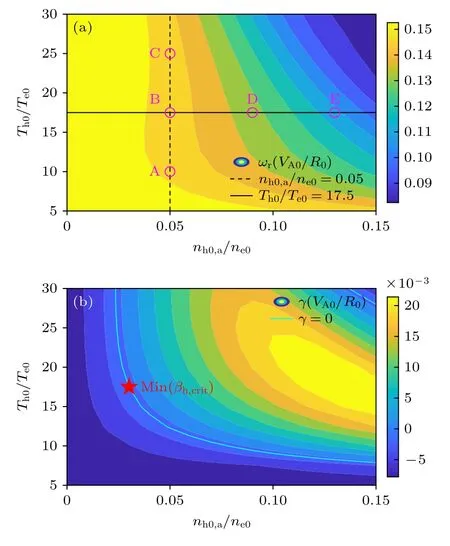
图5 e-BAE (a)实频率和(b)增长率随高能量电子密度和温度的依赖关系.A—E 为参数空间下的5 个代表算例,用于下一步模结构分析.青蓝色实线为e-BAE 临界不稳定边界 (γ=0),五角星为激发e-BAE 需要的最小高能量电子比压对应的密度和温度值Fig.5.The e-BAE (a) real frequency and (b) growth rate dependences on energetic electron (EE) density and temperature.A—E are five typical cases for next mode structure analysis.Cyan solid line represents the boundary of marginal stable e-BAEs with γ=0,and the pentagram marks the EE density and temperature locations of the minimal value of EE βh required for e-BAE excitation.

3.4 e-BAE 模结构对称性破缺

如前文所述,e-BAE 模结构具有“回旋镖”形状特征,属于典型的极向对称性破缺,为了进一步明确nh0,a和Th0对e-BAE 模结构的影响,将图5(a)中A—E 五个算例分为两组进行内部比较: 算例A,B,C 中高能量电子密度相同nh0,a=0.05ne0,温度分别为Th0/Te0=10,Th0/Te0=17.5和Th0/Te0=25 ;算例B,D,E 中高能量电子温度相同Th0/Te0=17.5,密度分别为nh0,a=0.05ne0,nh0,a=0.09ne0和nh0,a=0.13ne0.如图6 所示: 算例A,B,C 中模结构的“回旋镖”形状特征依次增强,并且对于m=6的主极向分量,其相位角沿着径向的变化增大(蓝色实线),说明有限Th0对应的非微扰效应既导致ωr降低,也加剧了模结构的极向对称性破缺.如图7 所示,算例B,D,E 中模结构的“回旋镖”形状相似,m=6 主极向分量的相位角θr变化也基本一致,说明有限nh0对应的非微扰效应主要引起ωr降低,而对e-BAE 模结构的影响很小.

图6 (a1)—(c1)图5 中A,B,C 算例的静电势 δφ 二维模结构;(a2)—(c2) A,B,C 算例中主极向分量 δφm=6 及其相位角θr=arctan的径向剖面,灰色阴影部分表示e-BAE 有限振幅区域Fig.6.(a1)-(c1) The 2D poloidal mode structures of electrostatic potential δφ for cases A,B and C in Fig.5;(a2)-(c2) the radial profiles of dominant principal poloidal harmonic of δφm=6 and corresponding phase angle θr=arctan,and the gray shaded region represents the radial domain with finite e-BAE amplitude.

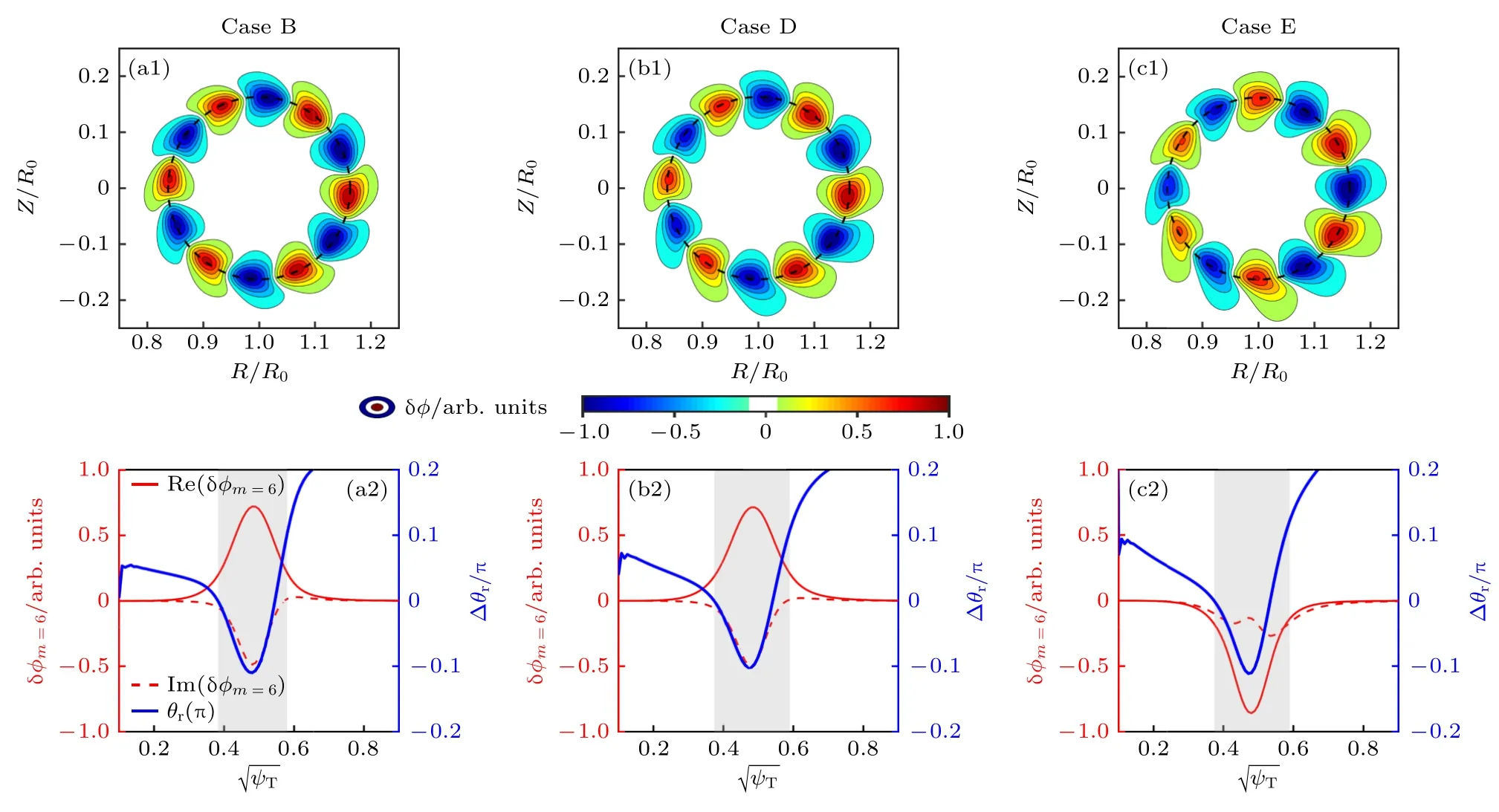
图7 (a1)—(c1)图5 中B,D,E 算例的静电势δφ 二维模结构;(a2)—(c2) B,D,E 算例中主极向分量 δφm=6 及其相位角θr=arctan的径向剖面,灰色阴影部分表示e-BAE 有限振幅区域Fig.7.(a1)-(c1) The 2D poloidal mode structures of electrostatic potential δφ for cases B,D and E in Fig.5;(a2)-(c2) the radial profiles of dominant principal poloidal harmonic of δφm=6 and corresponding phase angle θr=,and the gray shaded region represents the radial domain with finite e-BAE amplitude.

高能量电子非微扰效应不仅使e-BAE 模结构产生极向对称性破缺,当其密度或温度梯度的特征长度剖面(即 |R0/Ln,h| 或 |R0/LT,h|)关于有理面不对称时,还会引起模结构的径向对称性破缺.通过变化最强驱动 |R0/Ln,h|max与q=2 有理 面的 相对位置,选取了3 个算例分析径向对称性破缺,如图8(a)所示,采用图5 中算例C的nh0,a=0.05ne0和Th0/Te0=25 参数作为“零偏移(zero shift)”算例,向左和向右移动nh0剖面作为“左偏移(left shift)”和“右偏移(right shift)”算例.如图8(b)所示: “左偏移”、“零偏移”和“右偏移”算例中|R0/Ln,h|max对应的径向位置分别为rmax(-R0/Ln,h)/a=0.41,rmax(-R0/Ln,h)/a=0.49和rmax(-R0/Ln,h)/a=0.57,并且只有“零偏移”算例的 |R0/Ln,h|max位置与q=2 有理面重合.图9(a1)—(c1)分别为“左偏移”、“零偏移”和“右偏移”算例的 δφ二维模结构: 当最强驱动|R0/Ln,h|max的径向位置向左和向右偏离q=2 有理面时,δφ模结构强度分布也向左和向右偏移,“回旋镖”模结构产生显著的径向不对称性.图9(a2)—(c2)为m=6 主极向分量及其相位角θr,发现只有“零偏移”算例中相位角变化 Δθr的极值点在灰色阴影区域的中间(即关于q=2 有理面对称),而“左偏移”和“右偏移”算例中 Δθr极值点分别在灰色阴影区域的右侧和左侧,与 δφ模结构强度分布偏移正好相反.

图8 (a)固定高能量电子在磁轴处的密度 nh0,a/ne0=0.05,向左和向右移动高能量电子密度剖面;(b)对应的密度梯度特征长度剖面Fig.8.(a) Fix the on-axis EE density with nh0,a/ne0=0.05 and shift the density profile left and right;(b) the corresponding gradient scale length profiles.

径向对称性破缺还会导致 δφ扰动在平行波数k//=(nq-m)/(qR0)谱空间中分布不对称,从而产生有限 〈k//|δφ|2〉V及相应的残余协强(〈·〉V代表体积平均值),是驱动等离子体自发旋转的重要机制之一[26].基于图9 中3 个算例的模结构,计算相应的k//|δφ|2径向剖面和体积平均值 〈k//|δφ|2〉V,如图10(a)和图10(b)所示,发现“左偏移”和“右偏 移”算例的k//|δφ|2剖面 关于q=2 有理面不 对称,并且 〈k//|δφ|2〉V具有有限值;“零偏移”算例具有对称的k//|δφ|2,由于正负区域相互抵消导致〈k//|δφ|2〉V接近于零.以上计算表明当高能量电子驱动强度关于有理面分布不对称时,e-BAE可以引起有理面附近局域的等离子体自发旋转.

4 总结和讨论

为了深入理解e-BAE 不稳定性特征,本文利用自主开发的MAS 本征值程序开展全域动理学模拟研究.模拟采用朗道流体模型描述主等离子体,漂移动理学模型描述高能量电子,非微扰地在参数空间下计算e-BAE 模结构、实频率和增长率.主要结果和发现如下:

1)随着环向模数n增大,e-BAE 所在的阿尔芬连续谱势阱宽度变窄,从而导致e-BAE 径向模结构宽度变窄;但BAE-CAP 频率不随n变化,因此e-BAE 频率随n变化很小;e-BAE 增长率受到进动共振匹配条件的影响,随n先增大后降低.

2)本文的亮点是通过计算不同nh0,a和Th0下e-BAE 实频率和增长率,发现高能量电子非微扰效应可以定性改变e-BAE 色散关系图谱: 即e-BAE实频率随nh0,a增大而显著降低,进而影响共振条件导致增长率随nh0,a先增大后降低.而传统微扰方法则认为阿尔芬本征模实频率不受nh0,a的影响,增长率随nh0,a单调增大.另一方面,e-BAE 实频率和增长率随Th0的变化与nh0趋势相似,导致e-BAE增长率在nh0,a-Th0参数空间存在不稳定岛,而微扰方法下则不存在不稳定岛.

3)高能量电子非微扰效应引起e-BAE 模结构对称性破缺.当驱动强度剖面 |R0/Ln,h| 关于有理面对称时,δφ二维模结构仅产生极向对称性破缺,呈现沿极向上-下不对称但关于有理面对称的“回旋镖”特征;当 |R0/Ln,h| 剖面关于有理面不对称时,δφ二维模结构同时存在极向和径向对称性破缺,即“回旋镖”模结构不再关于有理面对称,通过计算发现径向对称性破缺可以产生有限 〈k//|δφ|2〉V并引起等离子体自发旋转.

本文重点分析了高能量电子非微扰效应对e-BAE 线性性质的影响.下一步计划研究主等离子体温度、密度以及高能量电子各向异性分布函数的影响,并结合机器学习在参数空间下训练高效代理模型[27],为理解和预测实验上e-BAE 不稳定性提供支持.

感谢核工业西南物理研究院陈伟研究员和浙江大学仇志勇教授的讨论.