基于GAPSO和自抗扰控制的稀土永磁同步电机性能研究

陈 苗， 温 俊

（江西铜业股份有限公司德兴铜矿，江西 德兴 334200）

稀土永磁同步电机的永磁体选用的是高性能稀土钕铁硼材料， 相比其他永磁同步电机， 稀土永磁同步电机具有电磁强、 效率高、 性能好的优势，广泛应用于矿山机械、 化工、 新能源汽车、 医疗器械等领域［1-3］。然而， 稀土永磁同步电机的控制系统具有参数不确定性、 复杂时变性与系统非线性的特点， 其控制性能直接决定电机的转速性能及应用价值， 因此对其进行控制方法的研究具有深远的意义［4］。

国内外稀土永磁同步电机的控制方法层出不穷［5-11］。朱熀秋等［7］提出了一种磁悬浮稀土永磁同步电机的直接转矩直接悬浮力控制方法， 首先建立直接转矩控制模型， 再将其应用至悬浮模块， 进而建立直接悬浮力控制模型， 并通过仿真验证了该方法的有效性。在此基础上， 魏海峰等［8］设计了一种基于锁相环磁链调制的控制方法， 仿真和实验结果表明， 该策略能满足目标所需的控制精度，且具有较好的稳定性。值得一提的是， 自抗扰控制方法在控制精度、 响应速度和稳定性上具有独特的优势［8-9］。张臻等［10］发现了一种复杂变结构的PMSM 自抗扰控制方法， 将滑模变结构控制的思想引入自抗扰控制中， 提高了自抗扰控制的位置跟踪精度。针对传统自抗扰控制存在观测精度差的问题， 朱德明等［11］提出将卡尔曼滤波器与自抗扰控制相结合， 通过对反馈律的非线性化， 进而减少电机在控制时的误差［11］。虽然自抗扰控制及其改进控制方法在稀土永磁同步电机控制上具有较好的效果， 但也存在参数选定不合理的问题。此时，可以采用粒子群算法来解决上述问题， 该算法可以自动寻优， 帮助完成参数选定［12-13］。

因此， 本文提出一种基于遗传粒子群算法（GAPSO）的稀土永磁同步电机自抗扰控制方法，为提高电机的控制性能探索了一条研究的新道路。

1 工程背景及数学模型

江西铜业股份有限公司德兴铜矿在采矿和选矿等场所的大型矿山机械设备中均要用到稀土永磁同步电机， 其工作原理如图1所示。稀土永磁同步电机由定子、 转子和绕组等组成， 转子上含有稀土永磁体， 通过往绕组通三相电形成电磁场， 与永磁体磁场叠加形成力矩进而带动转子旋转。

图1 稀土永磁同步电机工作原理图Fig.1 Schematic diagram of the rare-earth permanent magnet synchronous motor

稀土永磁同步电机的控制性能决定了采矿、选矿等工作效率。为此， 本文首先推导出稀土永磁同步电机的力矩表达式。研究永磁同步电机的控制需要在d-q坐标系下， 同时不考虑磁路饱和、磁滞和涡流损耗导致的误差。当采用矢量控制时， 稀土永磁同步电机的数学模型可用式（1）表达：其中，Id和Iq为引线电流到d和q轴的投影；ω为稀土永磁同步电机的转速；Ld和Lq为引线电感到d和q轴的投影；ud和uq为引线电压到d和q轴的投影；p为极对数；R为引线电阻；J为稀土永磁同步电机旋转时的转动惯量；F为电机所受到的负载力；Tm为电机所受到的负载转矩；ψF为稀土永磁同步电机磁链的峰值大小。

本节建立的转矩模型可为稀土永磁同步电机自抗扰控制器的设计奠定模型基础。

2 自抗扰控制器设计改进

2.1 常规自抗扰控制器的设计

常规自抗扰控制是根据传统比例-积分-微分（PID）控制改进而来的， 进一步提高了系统的抗干扰能力， 其控制原理如图2所示。

图2 常规自抗扰控制的原理框图Fig.2 Schematic block diagram of traditional active distur bance rejection control

由图2可知， 常规自抗扰控制对稀土永磁同步电机的信号处理包括跟踪微分器信号信息处理、扩张状态观测器确定各目标状态量以及非线性误差反馈控制律3个环节［14］。

1）跟踪微分器

跟踪微分器作为信号的前处理器， 相当于介入一个微分环节， 其作用是使信号柔软化， 进而获得高速度无超调的控制信号。其方程可表示为式（2）：

其中，h为积分步长； fst 为跟踪速度指标；h0为滤波因子；rref为控制系统的给定信号；x1表示处理过后的跟踪信号；x2表示跟踪微分信号。跟踪微分器性能的优劣受性能参数（h，λ，h0）的影响较大， 比如λ越大， 系统跟踪的时间越短；h0越大， 响应时间越长， 表示系统不能快速进入稳态。

2）扩张状态观测器

扩展状态观测器是一个观测系统状态变量的装置， 它通过获取跟踪微分器处理后的信号信息，进而确定各个目标状态量。其状态方程可表示为式（3）：

其中，rfdb（k）表示控制系统的输出信号；z1（k）表示跟踪系统的输出信号；z2（k）表示z1（k）信号的微分信号；z3（k）表示观测器在控制过程中的全部干扰项；h为积分步长；u（t）为系统控制量。

3）非线性误差反馈控制律

该部分位于反馈环节处， 它的状态方程可表示为式（4）：

其中，e1表示控制系统的误差；e2表示控制系统误差的积分； ∂3和∂4表示反馈环节中的非线性因子；β01和β02分别表示系统误差以及误差微分的比例因子。式（3）fal的表达式如式（5）所示：

其中，ε表示控制系统的偏差； ∂表示非线性因子；δ表示滤波因子， sign（）为符号函数。

fal 函数作为非线性误差反馈控制律的重要组成部分， 极大影响了电机的控制性能。但fal 函数存在一个明显缺陷， 其在两个拐点处平滑度不足，这会使得系统出现抖振现象， 进而影响自抗扰控制器的控制精度。为了解决这一问题， 本文引入了平滑性更优的sigfal 函数， 其表达式如式（6）所示：

2.2 GAPSO对自抗扰控制器的参数优化

由2.1 节可知， 自抗扰控制器中有较多的性能参数需要给定， 这些参数的优劣决定了控制器是否能高效稳定地工作。而常规自抗扰控制对于参数的选定往往为手动调整， 控制精度不高， 经常出现系统达不到最优的情况。针对该情况， 本文提出采用GAPSO 来解决稀土永磁同步电机自抗扰控制器中的参数选定问题［15］。

GAPSO 能够在大幅度提高计算精度和收敛速度的同时， 使优化结果跳出局部最优。GAPSO 前半部分与传统粒子群算法（PSO）一致， 只是在更新位置和速度时加入了选择、 交叉、 变异算子， 可以有效改善传统粒子群算法存在的精度不高、 收敛差、 计算速度慢等问题。

根据图3 的优化流程， 可总结出基于GAPSO优化的稀土永磁同步电机自抗扰控制的具体步骤：

图3 GAPSO优化流程Fig.3 GAPSO optimization process

1） 推导出电机转矩的数学表达式；

2） 基于第1 步的数学表达式和2.1 节的步骤，设计滑模控制器；

3） 采用GAPSO 对稀土永磁同步电机自抗扰控制器中的参数进行选定；

4） 将基于GAPSO 优化的自抗扰控制方法写成代码， 并开展仿真研究。

3 仿真研究

为了验证经过GAPSO 优化后的自抗扰控制方法在稀土永磁同步电机上应用的有效性， 开展了仿真研究。在MATLAB/ Simulink 中建立出基于GAPSO 算法优化的稀土永磁同步电机自抗扰控制框图， 如图4所示。为了凸显控制方法的抗干扰能力和应对突发状况的水平， 在仿真时设置了干扰信号。电机参数如表1所示。

表1 稀土永磁同步电机参数表Table 1 Parameter table of rare earth permanent magnet synchronous motor

图4 基于GAPSO算法优化的自抗扰控制系统框图Fig.4 Block diagram of the optimized active disturbance rejection system based on GAPSO

本研究在仿真时加入了传统PID 控制、 常规自抗扰控制， 并和改进的自抗扰控制方法进行了对比。图5 为3 种不同控制方法的转速性能曲线， 可以看出几种方法的转速均可在0~0.1 s 时迅速上升至给定转速值， 之后转速趋于稳定。在0.3 s与0.7 s时转速曲线略有波动， 这是因为在这两个时刻增加和卸载了干扰信号， 以观察控制器的抗干扰能力。经对比分析发现， 传统PID 控制方法虽然反应迅速， 很快到达稳定状态， 但在启动、 加载和卸载时的超调量和调节时间是最大的。在矿山实际应用环境中， 可能会产生较大的抖振， 甚至发生危险； 而采用自抗扰控制时， 上述指标表现得更加优异。从图5可以明显看出， 不管是启动时刻还是加入干扰信号， 两种自抗扰控制曲线的超调量和调节时间均在一个较小的范围， 而且曲线过渡更加平滑， 系统的调节时间也更短。

图5 Simulink仿真结果Fig.5 Simulink simulation results

从图5的局部放大图可以看出， 相比于常规自抗扰控制， 改进的自抗扰控制方法响应速度更快、超调更小、 性能更优， 这说明GAPSO 算法对参数的优化效果显著。综上可以得出， 基于GAPSO 算法优化的自抗扰控制策略比PID 和常规自抗扰控制要好。

为了定量分析几种方法的差异， 将3种控制方法能表征控制性能的重要指标（超调量、 调节时间、 控制精度）进行汇总， 结果如表2所示。

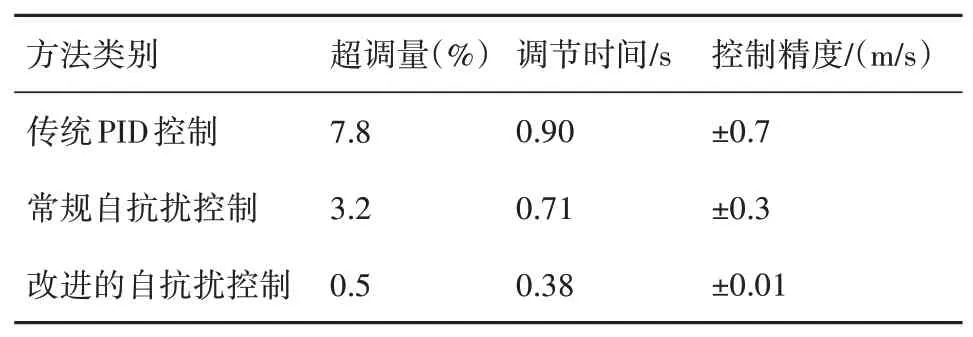
表2 各控制方法的数据结果Table 2 Data results of various control method

由表2可知， 改进的自抗扰控制方法的超调量仅为0.5%， 调节时间仅0.38 s， 控制精度约为±0.01 m/s。相对于传统PID 控制和常规自抗扰控制， 改进的自抗扰控制在超调量上分别降低了93.6%和84.4%， 在控制精度上分别提高了98.6%和83.3%， 在受到干扰时的响应时间缩短了57.8%和46.5%， 验证了优化后的自抗扰控制方法具有更好的动态性能和稳定性。

上述分析的是系统阶跃响应情况。为了进一步验证方法的有效性， 开展正弦跟踪仿真实验。对设置机械角度为20°的正弦波幅值进行测试， 同时加入传统PID 控制和常规自抗扰控制， 分别对3种控制方法进行对比分析， 其他控制参数不变。

由图6 可知， 3 种方法均能实现对目标期望信号的跟踪， 但跟踪精度有较大差别。传统PID 控制在跟踪时存在略微滞后， 且跟踪曲线没有自抗扰控制的跟踪曲线光滑， 说明自抗扰控制优于传统PID 控制。再对比2 种自抗扰控制的跟踪曲线， 发现常规自抗扰控制在波峰和波谷误差较大， 且跟踪精度远不及改进的自抗扰控制。而改进的自抗扰控制跟踪曲线基本与目标信号曲线重合， 跟踪精度较高。由此可见， 改进的自抗扰控制表现出了优秀的动态转速性能和控制效果， 更适用于高精度的控制系统。

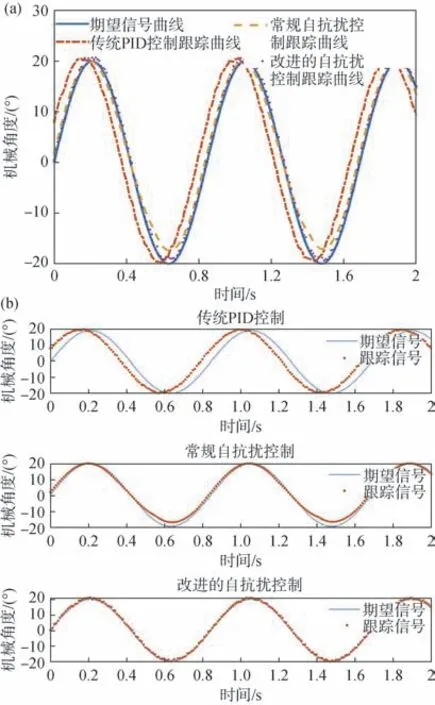
图6 3种控制方法的效果对比图（a）对比曲线； （b）各自的跟踪曲线Fig.6 Effect comparison diagram of three control methods（a） Contrast curves； （b） Respective tracking curves

上述分析说明， 在正弦谐波响应上， 基于GAPSO 算法优化的自抗扰控制策略也优于传统PID控制和常规自抗扰控制。

4 结束语

本文提出了一种基于GAPSO 优化的自抗扰控制方法， 并将其用于稀土永磁同步电机转矩控制中。仿真结果表明， 相较于传统EID控制方法和常规自抗扰控制方法， 改进的自抗扰控制方法在控制精度、 响应速度和稳定性等性能指标上得到大幅改善， 显著提高了稀土永磁同步电机的控制性能。而且基于GAPSO 优化的自抗扰控制方法在电机控制技术领域具有一定的通用性， 对异步电机、感应电机等各类电机的控制系统设计同样具有重要的参考价值。

下一步将通过控制系统的优化设计使稀土永磁同步电机的转矩特性和自抗扰能力更加适应复杂的大型矿山环境， 以提高其应用价值。