基于IGWPSO-SVM的HMCVT湿式离合器摩擦副温度预测

鲁植雄 王雨彤 王 琳 赵一荣 王兴伟 周俊博

(1.南京农业大学工学院, 南京 210031; 2.拖拉机动力系统国家重点实验室, 洛阳 471039)

0 引言

液压机械无级变速箱(Hydro mechanical continuously variable transmission,HMCVT)因具有操作简便、可自动调速等优点被广泛应用于重型拖拉机[1-3]。湿式离合器作为重型拖拉机HMCVT连接、切断动力源的关键传动部件,其工况与拖拉机性能直接相关,一旦湿式离合器摩擦副发生热失效,将严重影响整机的工作性能及安全性能[4-7]。

搭建温度预测模型对重型拖拉机HMCVT湿式离合器摩擦副温度进行预测,可有效防止摩擦副温度过高,对确保重型拖拉机传动系统工作可靠性是非常必要的[8]。然而,重型拖拉机HMCVT湿式离合器长期处于高噪、重载、参数时变等多干扰工作环境,其摩擦副温度预测仍是研究的热点与难点。一般地,通过理论计算与有限元分析方法得到的离合器摩擦副温度预测结果较为准确,BAO等[9]基于ANSYS对比研究了湿式离合器不同槽形摩擦盘的温度场,为离合器摩擦副结构设计提供了技术方案;GROETSCH等[10]基于KUPSIM软件搭建了湿式离合器温度预测模型预测湿式离合器换挡时的温度变化,试验结果表明,该模型在多种载荷工况下的温度预测误差较小,预测温度与实际温度之间的偏差在5K以内;陈楠[11]利用ABAQUS软件对HMCVT湿式离合器摩擦副进行了热-结构耦合仿真分析,得到了摩擦副不同半径节点处温度随时间变化的曲线及其温度场云图,较为准确地预测出摩擦副的温度变化规律。

然而上述的温度预测方法存在计算时间长、无法进行实时在线计算等缺陷,因而无法应用到湿式离合器实时温度预测中。近年来,随着人工智能的发展[12],基于机器学习的温度预测成为了研究热点:黄昌尧等[13]提出了一种基于长短时记忆(Long short term memory,LSTM)网络的分动器内离合器温度估计方法,利用离合器运行时的多种数据构建温度预测模型数据训练集,并借助LSTM构建了温度预测模型;范有才[14]提出了一种基于优化神经网络的湿式双离合器摩擦片温度预测方法,该方法通过湿式双离合器的热力学仿真模型获取了预测模型训练样本,采用遗传算法(Genetic algorithm,GA)优化反向传播(Back propagation,BP)神经网络的方式建立离合器摩擦片温度预测模型,该方法能够通过离合器摩擦副的其他参数快速地预测出摩擦片温度;周新志等[15]采用改进型粒子群优化(Particle swarm optimization,PSO)算法优化支持向量机(Support vector machine,SVM)的方法构建温度预测模型,试验结果表明,相比于未经优化的机器学习算法模型,该模型预测温度的标准差有所降低。然而,尽管单种群算法能够有效地优化温度预测模型,其仍存在随迭代收敛速度慢、易陷入局部最优等缺陷[16],难以保证离合器摩擦副温度预测精度。

基于以上现状,本文采用SVM作为湿式离合器摩擦副温度预测模型,并采用种群算法优化SVM。为解决单种群算法收敛速度慢、容易陷入局部最优等缺点,对其进行改进,提出改进型灰狼粒子群优化(Improved grey wolf particle swarm optimization,IGWPSO)算法。在湿式离合器摩擦副滑摩热分析的基础上,确定影响摩擦副温度的因素,基于HMCVT湿式离合器试验台数据搭建离合器摩擦副温度预测模型的样本数据库,以摩擦副对偶钢片为对象测试湿式离合器摩擦副温度预测模型的性能。

1 湿式离合器摩擦副滑摩热分析

HMCVT动力换段时湿式离合器摩擦副中的热量流动如图1所示。湿式离合器接合时,控制对应电磁阀通电,使得油泵加压后的液压油通过油道进入活塞的左侧空腔,此时活塞克服回位弹簧、波形弹簧的阻力,将摩擦片紧压在对偶钢片实现动力传递,当摩擦片与对偶钢片间转速差为零时即为完成接合过程[17]。

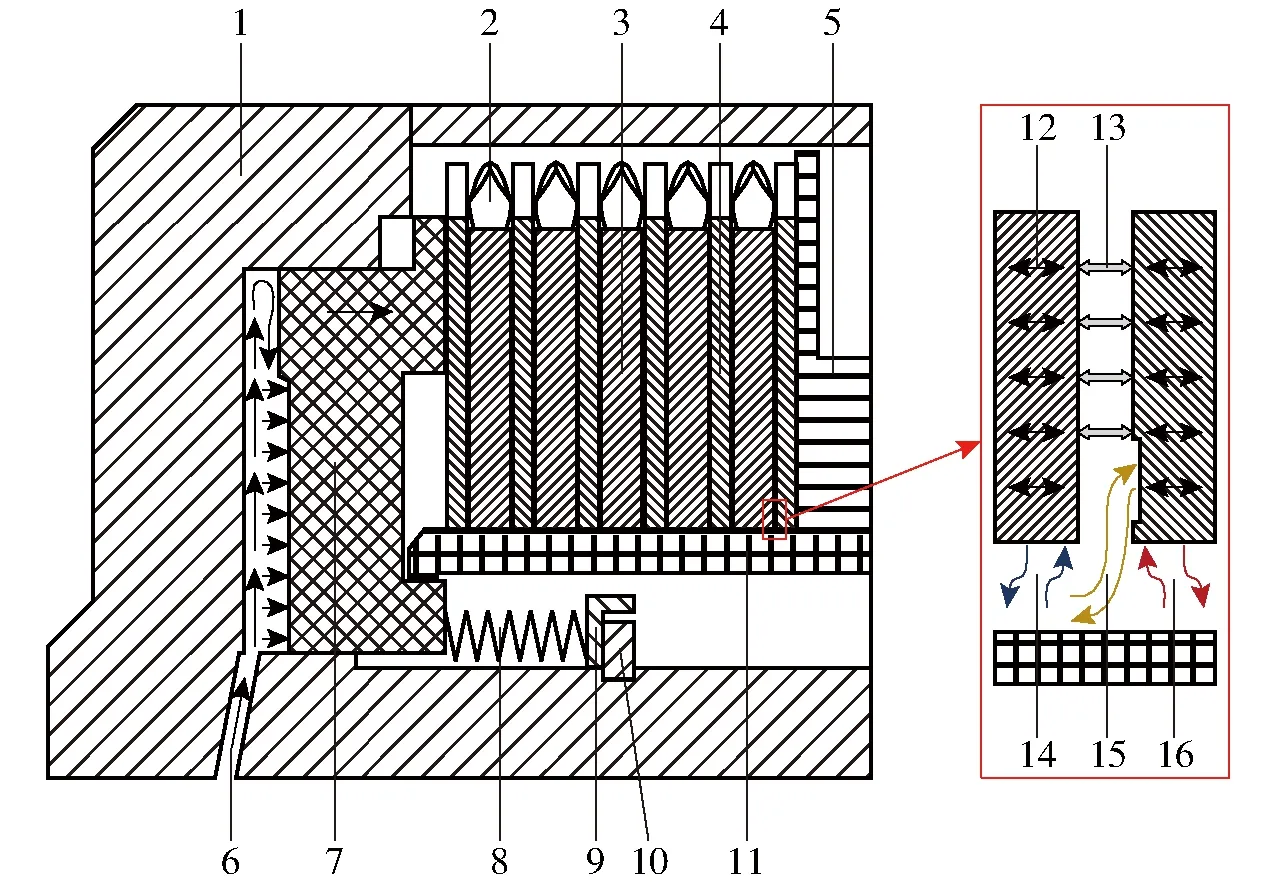
图1 HMCVT动力换段时湿式离合器摩擦副的热量流动示意图Fig.1 Schematic of heat flow of wet clutch friction pair during HMCVT power shift1.离合器缸体 2.波形弹簧 3.摩擦片 4.对偶钢片 5.齿毂挡圈 6.油道 7.活塞 8.回位弹簧 9.弹簧座 10.弹簧座卡簧 11.从动毂 12.热传导 13.摩擦热 14.摩擦片对流换热15.沟槽对流换热 16.对偶钢片对流换热

由图1可知,摩擦副的热量流动可分为3部分:第1部分热量为由摩擦副剧烈滑摩产生的摩擦热,分布在摩擦片和钢片两侧表面;第2部分热量由体表面以热传导方式传递到体中心;第3部分热量由摩擦片和对偶钢片通过冷却润滑油液介质以对流换热的形式散失,包括副间对流换热、沟槽对流换热及摩擦副内外环对流换热。

1.1 摩擦热

湿式离合器接合阶段摩擦副摩擦热计算如下:

将滑摩面划分成无数个宽度为dr的同心圆,同心圆上产生的摩擦力矩dM可表示为

(1)

式中F——滑摩面所受法向载荷,N

r——摩擦面上任意一点到中心轴的距离,m

A——滑摩面面积,m2

μ——摩擦因数

同心圆上的滑摩功dW为

(2)

式中 dω——摩擦副间的相对角速度,rad/s

则滑摩面的热流密度为

(3)

式中qh——滑摩面的热流密度,W/m2

摩擦副滑摩面上的热流密度随滑摩时间的变化公式为

q(t)=μrP(t)Δω(t)

(4)

式中q(t)——摩擦副滑摩面上的热流密度,W/m2

P(t)——摩擦副间的接触压力,Pa

Δω(t)——摩擦副间的角速度差,rad/s

在实际工况下,P(t)、Δω(t)随时间呈非线性变化,因此,湿式离合器滑摩时摩擦副间的角速度差和接合油压与摩擦热并非呈现标准线性关系[18]。

1.2 对流换热

对流换热的换热量用牛顿冷却公式计算,即

qd=h(Tg-Tl)

(5)

式中qd——对流换热的换热量,W/m2

Tg——固体温度,K

Tl——流体温度,K

h——对流换热系数,W/(m2·K)

湿式离合器摩擦副对流换热系数计算方式为

(6)

式中h1——滑摩前期副对流换热系数,W/(m2·K)

h2——摩擦副内外环面对流换热系数,W/(m2·K)

h3——沟槽对流换热系数,W/(m2·K)

λ——导热系数,W/(m·K)

Rer——旋转雷诺数

Pr——普朗特数

cr——螺旋管修正系数

ct——温差修正系数

L——润湿周长,即槽道横截面周长,m

v——流体速度,m/s

ν——运动粘度,m2/s

ρ——密度,kg/m3

c——定压比热容,J/(kg·K)

由伯努利方程可知,流体压强与流体速度相关,由此在滑摩过程中湿式离合器的接合油压将影响摩擦副的对流换热。但由于湿式离合器摩擦副温度和油液温度不断升高,导致油液性能也随之改变,因此有多种因素影响摩擦副间对流换热。

1.3 冷却润滑散热

图2为HMCVT冷却润滑油路系统,其功用为降阻降温,减少各零部件的磨损,提高整机耐用性等[19]。离合器接合过程中需冷却润滑系统对其进行冷却,若冷却油流量过小无法及时带走因滑摩产生的热量,将造成摩擦副局部温度过高,进而引发烧损。因此,冷却油流量通过影响冷却润滑系统的冷却效果,进而影响了湿式离合器摩擦副的温度。

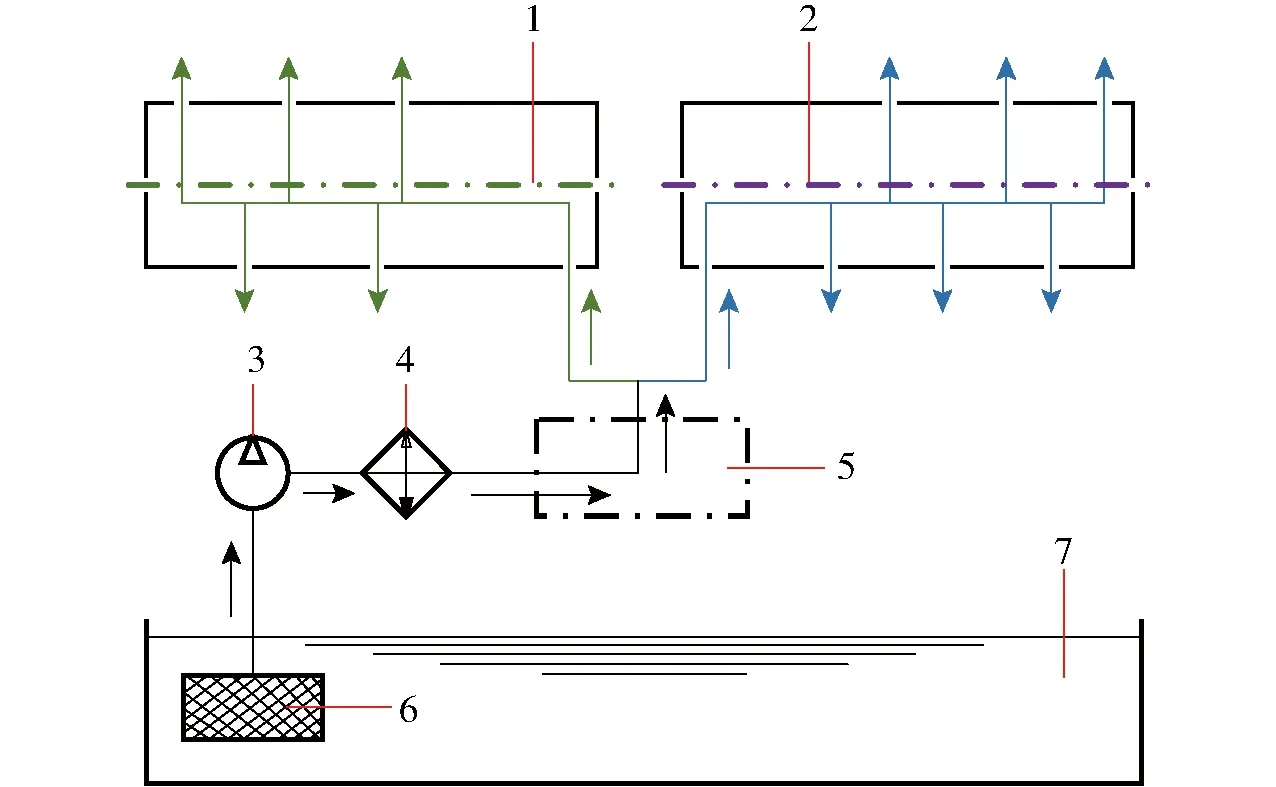
图2 HMCVT冷却润滑油路系统示意图Fig.2 Cooling lubricating oil circuit system of HMCVT1.段位离合器轴 2.前进/后退离合器轴 3.冷却润滑油泵 4.冷却器 5.阀体 6.过滤器 7.冷却润滑油

根据上述分析,摩擦副间角速度差、接合油压、冷却油流量分别通过影响摩擦热、对流换热、冷却润滑散热来影响湿式离合器摩擦副温度,且湿式离合器的初始油温能够直接影响摩擦副的温度。但以上4种影响因素与摩擦副温度之间的关系较为复杂,各个因素之间也有相互影响的情况,通过简单数学模型求解温度预测模型是困难的。

2 基于IGWPSO-SVM摩擦副温度预测模型

2.1 支持向量机(SVM)

SVM的基本思想是求解能够正确划分训练数据集并且几何间隔最大超平面,是一种机器学习算法。相比于其他机器学习算法,SVM可有效避免维数灾难和过拟合的问题,在处理复杂关系数据和数值预测等方面具有巨大优势[20-22]。因此本文采用SVM作为摩擦副温度预测模型。

2.2 IGWPSO算法

由于PSO算法具有收敛快、寻优范围大等特点,PSO算法已被广泛应用于参数寻优。PSO算法核心步骤有2个[23],即粒子更新速度公式和粒子位置更新公式[24]。灰狼优化(Grey wolf optimizer,GWO)算法是由MIRJALILI等[25]提出的新型种群算法。其原理效仿狼群的种群制度,将狼群分为α、β、δ、γ这4个种群,灰狼γ在狩猎过程中接受灰狼α、β、δ的支配。

然而,PSO算法具有收敛速度快、效率高等优点的同时也存在易陷入局部最优、收敛精度低等诸多问题,而GWO算法具有良好的全局寻优能力的同时也存在着不易收敛的缺陷[26-28]。基于上述算法的特性,对两种算法的结构进行改进,据此本文提出IGWPSO算法,设IGWPSO算法种群规模(个体数)为N;总迭代(进化)次数为T;个体目前迭代次数为t,个体目前位置为xt,个体目前移动速度为vt。

将PSO算法中引入一种非线性权值递减的变量权值ωv,IGWPSO算法的个体速度更新公式为

(7)

式中vt+1——更新后的粒子移动速度

ω——惯性权值

c1——个体学习因子

c2——社会学习因子

r1、r2——互不相同的[0,1]间随机数

pbest——粒子目前的个体最优解

gbest——粒子目前的全局最优解

ωmax——最大惯性权值

ωmin——最小惯性权值

e——自然常数

由式(7)可知,采用ωv后,PSO算法在前期粒子飞行速度快,具有较强的全局寻优能力,在后期粒子飞行速度慢,具有较强的局部寻优能力,在保障算法收敛速度的同时提高了算法的搜索精度。不同于线性权值递减,本文提出的非线性权值递减实现了对权值下降速度的控制:在算法前期惯性权值下降速度缓慢,使惯性权值维持在较高数值,通过增大粒子的跳动幅度提高寻优速度,进一步提升算法前期全局寻优能力;在算法后期惯性权值下降速度增快,使惯性权值迅速下降到较小数值,通过减小粒子的跳动幅度提高寻优精度,进一步提升算法后期局部寻优能力。因此,采用ωv能够使算法更好地平衡全局与局部寻优能力。

将GWO算法中的灰狼个体更新方式引入PSO算法的粒子位置更新公式中,IGWPSO算法的个体位置更新公式为

xt+1=xf(t+1)+vt+1

(8)

式中xt+1——更新后的粒子位置

xf(t+1)——个体经过GWO算法更新后位置

由式(8)可知,在IGWPSO算法中位置的更新由两部分组成,一部分是由粒子本身速度决定,另一部分是由α、β、δ引领作用下更新的位置所决定,结合了GWO算法和PSO算法个体位置更新方式的优势,增强粒子群粒子个体间的信息交流,扩大了粒子的寻优空间,算法收敛速度及寻优精度得以提升的同时算法跳出局部最优能力也得以提升。

研究发现在SVM训练过程中,惩罚因子c与RBF核函数自带参数g对SVM的性能具有较大的影响,因此本文采用IGWPSO算法优化SVM的2个参数c、g,据此提出改进灰狼粒子群优化-支持向量机(Improved grey wolf particle swarm optimization-support vector machine,IGWPSO-SVM)算法,IGWPSO-SVM算法流程如图3所示。

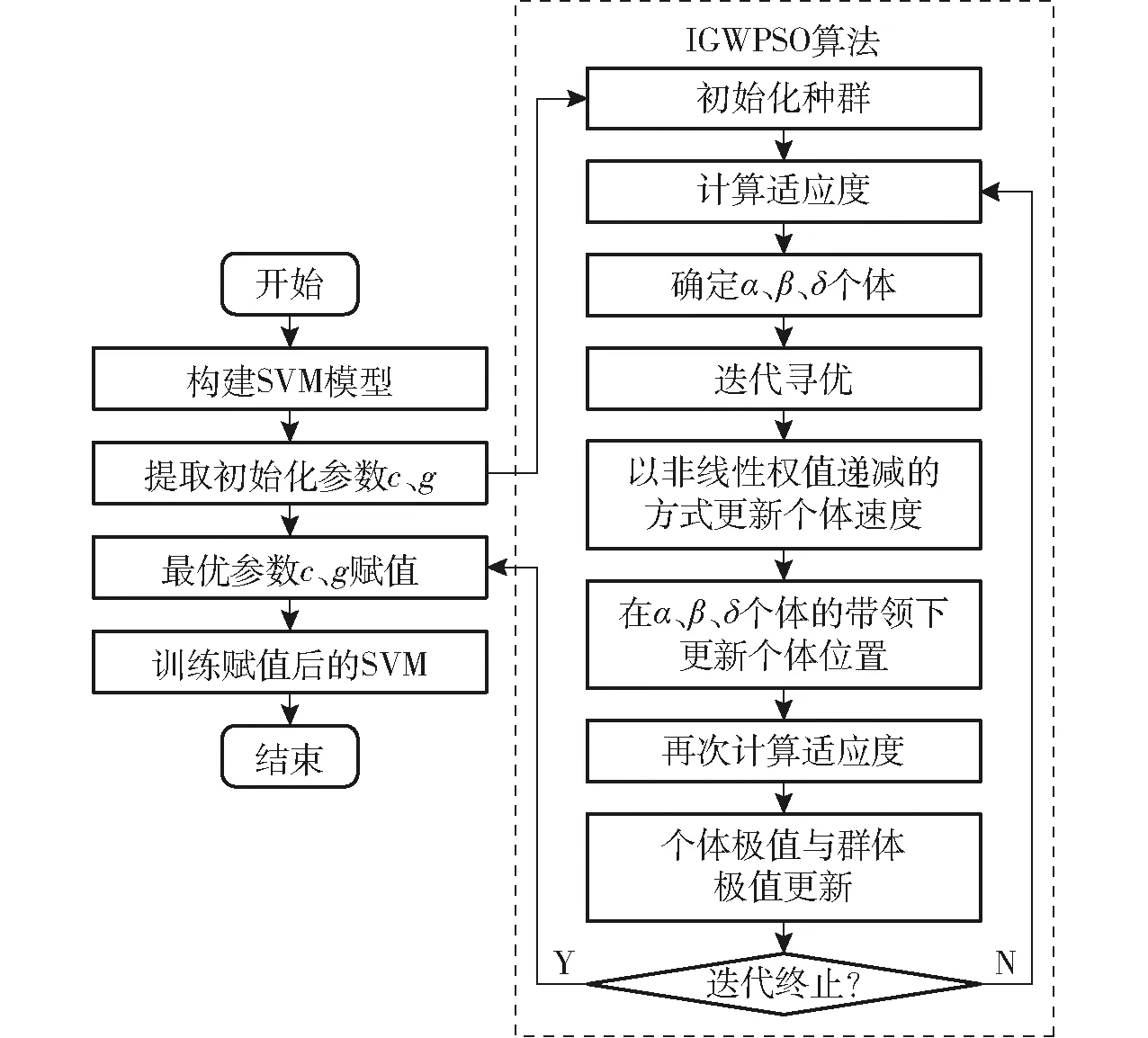
图3 IGWPSO-SVM流程图Fig.3 Flowchart of IGWPSO-SVM

IGWPSO-SVM模型流程具体为:确定SVM的结构模型,提取并初始化结构参数c、g;以SVM训练时的交叉验证准确率作为适应度函数,采用IGWPSO算法优化c、g;初始化种群,从种群中划分出个体α、β、δ,计算种群中所有个体的适应度,根据所有个体适应度更新种群中的个体α、β、δ;根据非线性权值递减的方式更新个体的速度,在个体α、β、δ的引领下更新个体的位置;再次计算个体的适应度,根据个体适应度更新种群与个体极值;判断是否满足算法终止条件,若为真将最优c、g赋值给SVM;训练最优c、g赋值后的SVM。

3 IGWPSO-SVM温度预测模型性能试验

3.1 试验方案

本文基于南京农业大学工学院自主研制的HMCVT湿式离合器试验台架开展IGWPSO-SVM模型性能试验,试验台架如图4所示。试验台架由变频电机驱动,型号YXVE315L2-4,额定扭矩1 286 N·m,调速范围0～1 450 r/min。通过德力西变频器调整电机输出功率。兰菱机电ZJ-A型转速转矩传感器转速量程0～3 000 r/min,转矩量程0～2 000 N·m。 加载装置为兰菱机电电涡流制动器,型号CWC2000,集成了转速传感器和转矩传感器。油压传感器为JPL131建胜油压变送器,量程0～10 MPa。温度传感器为WRNK-191 K型铠装热电偶,量程0～500℃。流量传感器为LWGB-10型,量程0～20 L/min。

图4 HMCVT湿式离合器试验台Fig.4 Test stand of HMCVT wet clutch1.润滑液压系统 2.电涡流测功机 3.转动惯量盘 4.离合器箱 5.转速转矩仪 6.电动机

根据前文分析可得,影响湿式离合器摩擦副温度的主要因素有转速差、初始油温、接合油压及冷却油流量,由此本文基于湿式离合器接合油压、冷却油流量、初始油温、输入轴转速、输出轴转速5种变量构建IGWPSO-SVM模型输入数据的样本库。其中湿式离合器接合油压、冷却油流量、初始油温、输入轴转速如表1所示。

表1 输入变量取值范围Tab.1 Value range of input variable

在湿式离合器接合过程中,由于摩擦材料的影响,对偶钢片整体温升相比摩擦片更高,其温度变化趋势更能反映摩擦副温度变化。因此,本文以对偶钢片为对象测试摩擦副温度预测模型性能。如图5,在对偶钢片内径(63 mm处)、中径(71 mm处)、外径(79 mm处)分别布置热电偶,并采集3处的温度数据构建IGWPSO-SVM模型输出数据样本库。

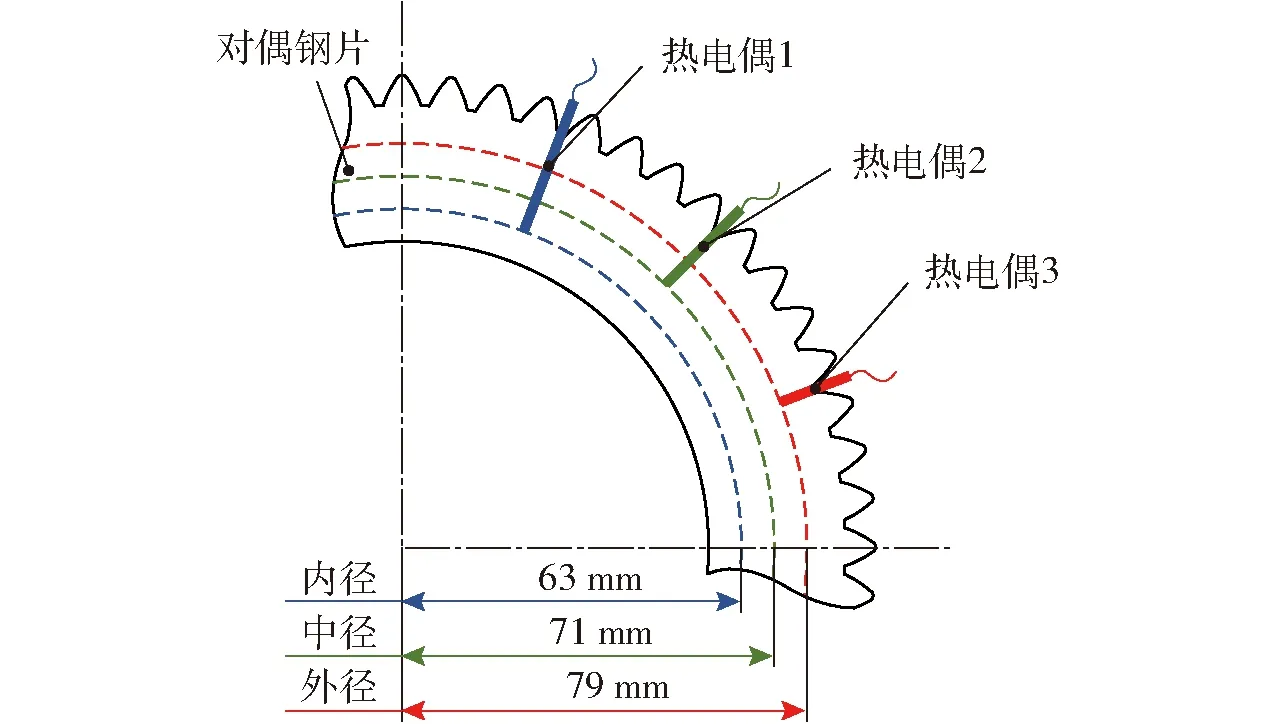
图5 热电偶在对偶钢片的安装位置Fig.5 Position of thermocouple in dual steel plate

根据上述试验方案,获取表1工况下湿式离合器连续2次滑摩前后及滑摩过程的数据,包括离合器接合油压、冷却油流量、初始油温、离合器输入轴转速、离合器输出轴转速及对偶钢片温度数据。其中200组作为IGWPSO-SVM模型的训练集,采用同种方法再获取另一种工况下的140组数据作为IGWPSO-SVM模型的测试数据,用以检验温度预测模型的预测准确性。由于样本数据中各数据数量级不同,为避免其对之后建立的温度预测模型精度的影响,采用归一化方法对样本数据进行处理,使所有模型的输入、输出变量集中在[-1,1]区间。

3.2 试验结果与分析

图6所示为IGWPSO-SVM训练与测试结果,表2为IGWPSO寻得的最佳参数解。

表2 最佳参数解Tab.2 Optimal parametric solutions

图6 IGWPSO-SVM训练与测试结果Fig.6 Training and test results of IGWPSO-SVM

为进一步验证IGWPSO-SVM温度预测模型的可行性,对BP神经网络模型、SVM模型、PSO-SVM模型、GWO-SVM模型与IGWPSO-SVM模型进行试验对比分析,选取预测温度与实际温度间的平均绝对误差(Mean absolute error,MAE)、均方误差(Mean square error,MSE)、均方根误差(Root mean square error,RMSE)、平均绝对百分比误差(Mean absolute percentage error,MAPE)衡量各个模型性能,结果如表3所示。图7为不同算法的适应度曲线。

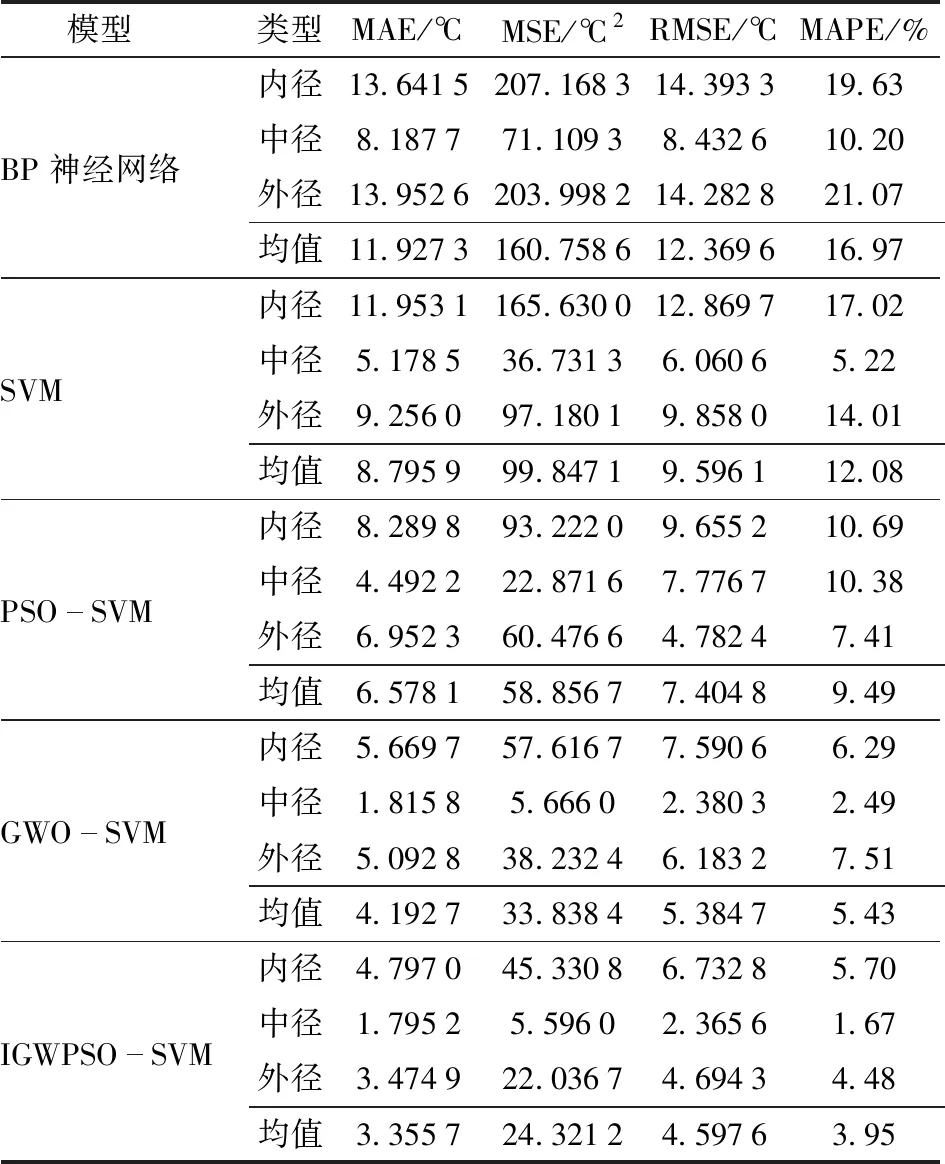
表3 不同模型的预测性能参数Tab.3 Predictive performance parameters for different models

图7 不同算法的适应度曲线Fig.7 Fitness curves of different algorithms

由表3可知,BP神经网络预测温度的MAE、MSE、RMSE、MAPE的均值分别为11.927 3℃、160.758 6℃2、12.369 6℃、16.97%,比其他4种模型都高,说明BP神经网络可能陷入了局部最优,未训练出合适的网络模型导致预测误差大;SVM预测温度的4种误差的均值较BP神经网络有所降低,说明SVM结构简单,训练压力小,能够训练出较精准的温度预测模型,提高了温度预测精度,但误差仍维持在较高水平;相较于SVM模型,PSO-SVM、GWO-SVM模型预测误差均有所降低,证明了种群算法优化SVM参数的可行性;对比PSO-SVM模型,GWO-SVM模型预测精度更高,说明GWO算法的寻优性能强于PSO算法,但观察图7可知,以内径温度预测为例,PSO算法迭代次数为10时算法完成收敛,最终收敛值为0.014 3,GWO算法迭代46次完成收敛,最终收敛值为0.013 5,说明PSO算法的收敛性优于GWO算法,而寻优精度不及GWO算法;相较于 PSO-SVM、GWO-SVM模型,IGWPSO-SVM模型预测温度的4种误差有所降低,分别为3.355 7、24.321 2、4.597 6、0.039 5℃,相比于其他模型均为最低,无论预测内径、中径、外径温度,相比于PSO、GWO算法,IGWPSO的收敛速度最快,最终收敛值最低。

预测湿式离合器接合时摩擦副的最高温度,可有效防止摩擦副温度过高导致的湿式离合器烧损失效。为验证IGWPSO-SVM预测模型的实用性,以最高温度的预测情况衡量各模型预测性能,表4为不同模型预测的最高温度。由表4可知,IGWPSO-SVM模型对摩擦副最高温度的预测误差为 7.870 0、5.430 0、0.990 0℃,相比于其他模型为最低,进一步验证了本文提出模型的实用性。

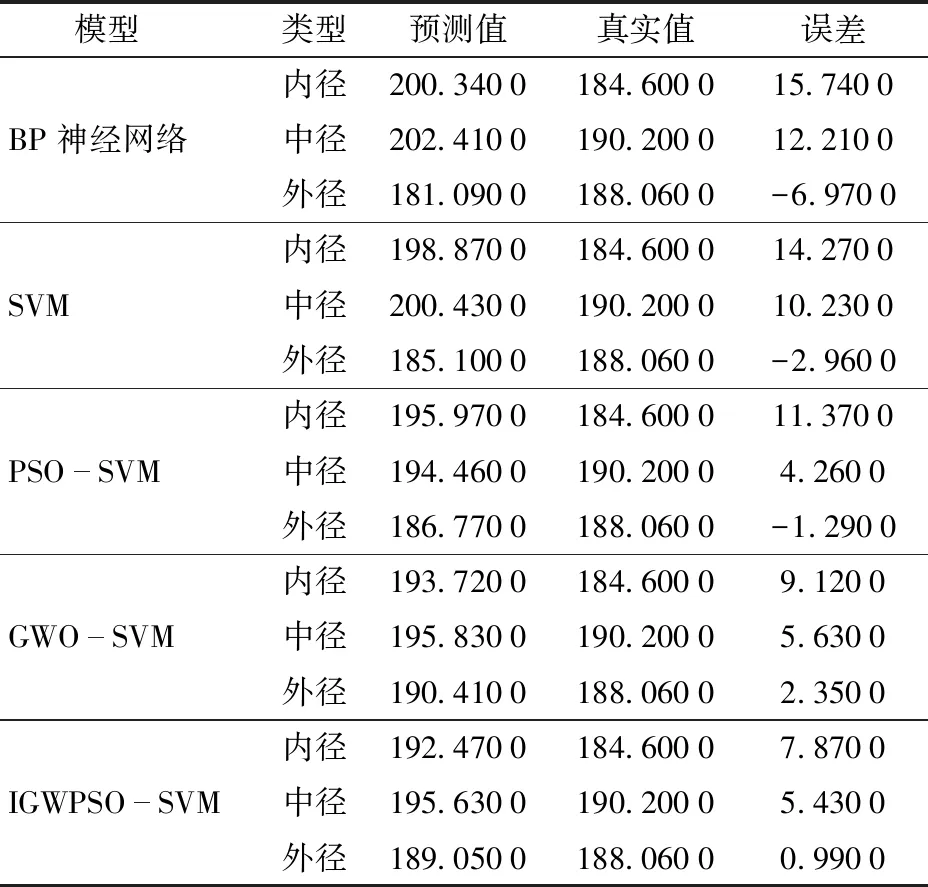
表4 不同模型预测的最高温度Tab.4 Maximum temperatures predicted by different models ℃

为避免算法随机性导致的偶然性,对5个模型进行3次同条件试验,选择内径、中径、外径的MAE、MSE、RMSE、MAPE均值及内径、中径、外径最高温度平均绝对误差(Maximum temperature mean absolute error,MTMAE)衡量模型性能指标,3次试验结果如表5所示。

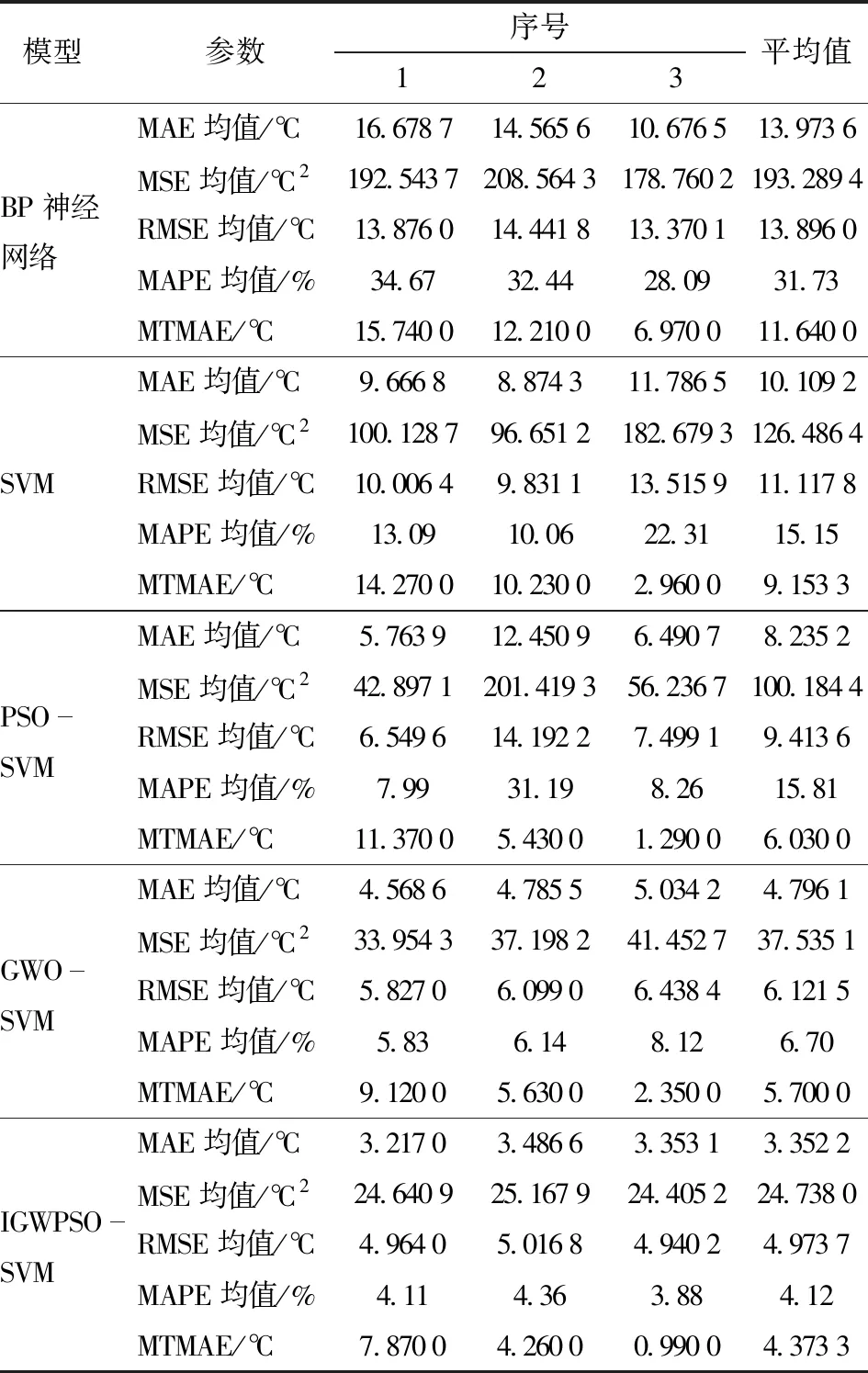
表5 多次试验结果Tab.5 Multiple experimental results

由表5可知,相比于BP神经网络,SVM多次预测的4种误差较小,说明在本文的温度样本数据下,SVM的预测性能较为稳定;PSO-SVM模型在第1、3次试验中温度预测误差达到较为理想的效果,但在第2次试验中,预测效果不及未优化SVM模型,导致3次试验预测误差平均值仍处于较高水平,说明PSO算法优化的稳定性欠佳;相较于PSO-SVM模型,GWO-SVM模型的3次预测误差均较低,证明GWO算法比PSO算法更加稳定;IGWPSO-SVM模型预测MAE、MSE、RMSE、MAPE均值的3次试验平均值分别为3.352 2℃、24.738 0℃2、4.973 7℃、4.12%,相较于其他模型为最低,同时单次预测误差均维持在较低水平,验证了IGWPSO-SVM模型的稳定性。同时,3次试验中IGWPSO-SVM模型的MTMAE平均值为4.373 3℃,相较于其他4种模型为最低,说明IGWPSO-SVM模型能够准确稳定地预测出湿式离合器接合过程中摩擦副的最高温度。

4 结论

(1)分析了HMCVT换段时影响湿式离合器摩擦副温升的因素,确定了摩擦副的转速差、冷却润滑流量、初始油温、接合油压4种影响摩擦副温升状况的因素。

(2)以SVM搭建了HMCVT湿式离合器摩擦副温度预测模型,采用PSO算法优化SVM参数,针对PSO算法的缺陷,提出了IGWPSO优化算法,借此搭建IGWPSO-SVM摩擦副温度预测模型。

(3)获取湿式离合器连续2次滑摩前后及滑摩过程的数据,进行温度预测模型性能试验。试验结果表明,IGWPSO-SVM模型预测摩擦副对偶钢片内、中、外径的MAE、MSE、RMSE、MAPE的均值分别为3.355 7℃、24.321 2℃2、4.597 6℃、3.95%,最高温度的预测误差分别为7.870 0、5.430 0、0.990 0℃,相比于其他4种模型为最低,说明IGWPSO-SVM模型具有较佳的预测精度;3次试验中MAE、MSE、RMSE、MAPE的均值平均值分别为3.352 2℃、24.738 0℃2、4.973 7℃、4.12%,3次试验中MTMAE的平均值为4.373 3℃,相比于其他模型为最低,说明IGWPSO-SVM模型具有较佳的稳定性。