基于点云数据的水利工程变形信息可视化研究
王柏恒 黄开鑫 曹 亮
(1.江西省自然资源测绘与监测院 江西南昌 330002;2.南昌市测绘勘察研究院有限公司 江西南昌 330038;3.新余市规划设计院 江西新余 338000)
1 引言
传统的变形分析都是通过各监测点的观测实现单点变形监测分析,随着三维激光扫描仪、LIDAR、移动测量等设备的出现,人们可以获取建筑物的点云数据。论文通过对点云数据进行细化处理,并使用Goemagic Studio 软件进行预处理,最后将处理的数据利用Goemagic Qualify 以及CloudCompare 进行模型、差分比较并分析,提取参数,结合特征点,找出变形区域。从而人们对点云数据有了一个整体的概念,同时在数据处理过程中,对Geomagic Studio 及Cloud Compare 等软件有了应用上的认知,结合其理论基础,了解整个点云处理流程,且在TLS 技术实验过程当中,通过多期数据的多角度对比,可以得出点云数据在水利工程监测分析上的优势非常明显。
2 点云数据采集与处理
2.1 三维激光扫描仪的工作原理
它的工作原理是:仪器中心点到闸站表面某点的倾斜距离,点方向的水平角和目标点的垂直角,最后由仪器计算出三维坐标[1]。点云可以较为真实地反映出三维空间结构形态,在进行一系列处理后,可实现三角网的构建,同时实时动态地进行变形分析。
2.2 静态数据处理
测量得出平差点数为7,单位权中误差比是1.1518,Tau 检验显著水平为1.00%,X2 理论范围在9.8862-45.5585 之间,X2 检验值是27.6435,X2 检验结果为True。本次实验的处理方式是采用基线解算,首先需要将将外业采集的静态数据导入HGO 软件中,设置好中央子午线投影坐标系后进行高度截止角、采样间隔等参数调整进行基线解算、同步环异步环的合格处理,最后进行生成控制点坐标。
2.3点云数据处理
由于地形条件的限制,仪器假设位置不是任意观测位置,所扫描的地物信息不完整,存在一定的盲区[2]。根据地形的复杂程度设定扫描间隔。当对多视图云进行拼接时,首先将相邻点云在Cloud Compare中进行拼接。同时,由于TLS 在扫描过程中可能受视角和地物遮挡的影响,因此需要经常对被测物体进行多站扫测,这样采集的多站点云都处于自己的独立坐标系中,在后续的数据处理和三维重建中就需要对点云进行配准。
3 点云数据三维重建
3.1 三角剖分法
三角剖分法主要适应于地形比较复杂的一些地物,并且对于所有形状的拓扑结构都可以适用。该方法对于测物的三维重建具有一个较高的建模精度及理想的三维模型逼近效果。以三角网的方式进行建模从而更好地逼近真实地物就是三角剖分法的主要方式。
3.2 基于特征提取的重建法
为反映出曲面形状的自由度,同时检测出尖锐点,可以利用局部特征的权值来达到这一目的,该方法不仅可以间接过滤,而且可以提取更稳定可靠的特征点。首先建立特征点最下生成树实现点到线的转换,然后使用特征线进行三次平滑处理就可以很好地满足建模精度要求。而在特征点的提取过程中,对特征点和普通点赋予不同权重会带来局部偏差,尤其是在边界点的权重赋值中,会产生较大误差。
3.3 切片法重建
我们通过外业采集手段获取的点云数据少则几百万,多则上千万,但是其中有大量的点不是有效的三维建模数据。而点云数据预处理本质是对点云进行重组,尽可能地呈现测物特征,减小数据冗余。该方法在去噪、压缩等处理方面都比较有效,但是分层数N和弦高阈值dmax 的确定是用切片法重建点云的难点。
4 变形信息可视化表达方法
4.1 基于标靶标志比较的变形信息提取
首先需要在监测区域均匀地布设多个固定的扫描标靶,同时应保持标靶和三维激光扫描仪之间的距离应小于50m,各标靶之间最好通视,测量仪器与测物之间不能超过200m,满足要求的情况下进行多期数据采集,获取监测区域的数据。同时在数据预处理过程中,可以通过提取扫描标靶数据,从而拟合出中心点坐标,得到多个标靶的三维空间位置随时间变化量。标靶标志法可能会出现如标靶不容易固定、布设等问题,因此其精度远不如全站仪[3]。
4.2 基于表面模型比较的变形信息提取
4.2.1 拟合平面比较法
基于最小二乘平面拟合方程式为:
然后根据最小二乘准则公式VTPV=min,进行等权平差后便可以得到参数值:
最后便可以得到点云拟合的平面方程。
4.2.2 基于DEM的变形比较
为获取不同的如剖面图三遍变形曲面图等来更好地反映变形情况,我们可以通过如MATLAB 等制图软件来生成;在一般的水利工程闸站监测中,为了可以更加直观地分析出目标区域的变化量,我们首先需要利用TLS 获取到的点云数据生成闸站的表面模型,然后便可以利用不同时期的DEM 数据得到偏差值,从而生成偏差分析图。
4.3 基于色谱统计的变形结果分析
通过Hausdorff距离法比较得到点云在三维坐标方向的变化,同时该方法也可以对获取到的点云三位坐标偏差进行统计分析。本文提出利用色谱分析变形的方法,统计分析变形在三维坐标方向上的大小,得到闸站上各点变形随时间变化统计分布规律。
5 变形信息可视化实例
5.1 研究区概况
研究区为某市河闸,该河闸总长度虽然不足3千米,但是汇水面积却可达到10 平方千米。由于紧靠群山的原因,每次遇到下雨气候,洪水下泄就会导致河水水位暴涨。因此,整个项目的龙头工程为新建闸站,其中泵站设计规模为每秒可达50立方米,节制闸设计规模为每秒100立方米,是现有防汛标准的4倍以上。
5.2 点云数据处理
(1)点云拼接
由于试验对闸站先后进行了两次不同角度的扫描操作,从而保证了每次扫描后会得到约5000 万个点云,并且相邻站点间点云重叠大于20%。同时需要根据地形的复杂程度设定扫描间隔。在拼接过程中,首先需要使用cloudcompare 软件将相邻的点云进行拼接,然后拼接多视图点云,最后得到拼接后的两期点云数据。
(2)点云压缩
使用Geomagic Studio 将拼接好的数据进行删减,需要注意的是点云压缩并非随意地缩减数据,该保留的特征点是绝对不能剔除的。点云压缩后,剩下的点云数据依旧能表现物体本有之特征,且压缩后的两期数据形状要基本一致。
(3)点云去噪
我们主要利用Geomagic Studio 软件对点云数据进行去噪处理,目的是剔除点云粗差,同时将与后续曲面重建无关的数据去除掉,通过这种方式可以让点云模型更加平滑和准确,从而更好地保证了地物识别的准确性和对数据信息进行描述的精确性。通过去噪处理后得到的统计结果显示,最大距离为0.238717mm,平均距离为0.002549mm,标准偏差为0.006670mm。
(4)点云补洞
Geomagic Studio 软件有两种补洞的方法,分别是全部填充和填充单个孔。如果仅仅是小孔洞,可以手动选择空洞区域,并用填充点直接进行补点操作。如果是大孔洞,代表点云数据遗失严重,这种情况下可以建立参考面进行手动补点。若还有未能修补的小孔洞,则可待建立网格模型后自动补点。
(5)点云配准
1)基于标靶点配准
由于事先已经布置好控制点,两站数据的标靶点都置于控制点,本文对于基于标靶点配准主要使用realworks 软件找到同名标靶点,至少手动选择3个以上就可实现基于标靶点的点云配准,然后再对结果进行精配准,而后得到基于标靶点配准后结果。
2)基于控制点坐标配准结果
基于控制点坐标配准的结果主要是通过将坐标点数据在软件中进行输入后得到。
3)ICP配准
在四元数配准算法的基础上,阐述了一种曲面拟合技术,具体为从测量点集中确定对应的最近点的点集合,同时利用Faugera 提出的严密解决方案创造出点集对,并且将最近点点集计算出来,以此重复进行。如表1 所示为配准过程中运用到的变换矩阵。

表1 变换矩阵
5.3 基于点云数据的三维重建
首先在Poly Works 软件中将点云数据打开,然后使用其中的IM 检查模块计算出两期点云的体积并进行比对分析。具体步骤如下:
(1)将数据导入Poly Works 中,由于整个闸站数据较大,故只选取闸顶作为本次数据,并且通过点设置Z 值,同时为满足Delaunay 变形比较的需要,整个过程需保证Z 值小于滑坡表面高程。
(2)数据投影操作。打开软件中的树视图界面,选择1 号基准面,同时点击Crop 以此将三维场景可见栅格状平面点选为灰色,最后合适地框选住所有数据保证能投影至该Plane1,从而保证投影的闭合。
(3)点云数据的三角化。首先将所有的点云数据框选出来,然后点击编辑按钮,同时选择数据与参考元素,并点选三角数据点,最后将点云集合三角化。三角化参考面设置为1 号基准面-nom-。
5.4 变形信息可视化表达实例
5.4.1 基于点云差分比较的变形信息可视化结果
首先为了将获取到的点云数据保存为Cloud Compare 识别的格式,需要利用Geomagic Studio 12软件将数据框选出来,然后将操作后的两期点云数据在Cloud Compare 软件中打开进行差分比较。
(1)点集到点集ICP 的配准工作
首先将点云数据导入软件中,并且将错误差异设置为默认值,同时不勾选自由标度参数的选项;并将随机抽样限制数设定为20000,同时为进行最近点迭代配准,需要使用配准工具完成最临近点搜索。
(2)豪斯多夫距离计算
将完成ICP 配准工作的点集作为比较对象,同时另一组点集作为参考组。为得到两组数据最近点距离数据,需勾选multi-threaded 选项,进行豪斯多夫距离比对得到如下结果:

图1 Haosdorff距离计算
其对比结果如图可知,两组数据所有对应点里的Max distance 为3.7074mm,两 组 数 据 的Min distance 为0mm,Sigma为0.118231mm。
5.4.2 基于模型比较的变形信息可视化结果
首先将经过预处理后的点云数据导入软件,然后将两期数据实现数据配准,同时执行分析3D 比较,并将最大偏差值设置为10mm,依据手动设置的最大最小名义和临界值,按照不同的颜色段赋予变形量区间,最后建立变形量颜色分布图,并将两期点云数据进行色谱偏差对比分析。从图中可以很直观地看出XY和YZ方向的偏差:
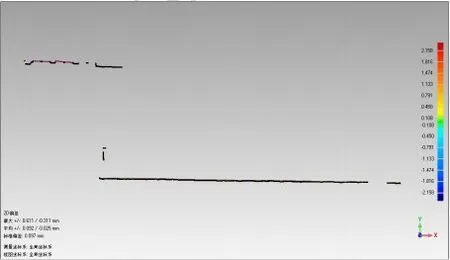
图2 XY方向偏差

图3 YZ方向偏差
5.4.3 变形结果分析
整体变形在2.063113mm-3699.114mm 之间,闸站侧翼变形量在31.9671mm-3699.114mm 之间,大部分变形在2.387353mm-93.97389mm 之间,主要产生较大误差的原因是:在对第二期点云数据进行扫描时,大部分闸站点没有采集到,整体闸站还是比较稳定。
6 结束语
论文首先使用CloudCompare软件将点云数据进行ICP 配准等预处理操作,同时将两期点云数据的Haosdorff Distance 差分进行比较,得出两期点云数据 间 最 大 距 离 为 3.7074mm,平 均 距 离 为0.0220138mm,标准差为0.118231mm,闸站体稳定,同时采用Geomagic Qualify 对闸站体进行3D 监测质量分析,利用ICP 算法进行局部匹配,并且为了更好地反映整体和局部的变形情况,建立了变形量—颜色分布图。结果显示:
(1)闸站体整体未出现明显变形,最大变形量为3.699114m,可能是由于1 期和2 期扫描时部分点云缺少,导致寻找的同名点误差较大,变形结果有较大误差;
(2)3D 的标准偏差在0.178mm-0.360mm 之间。XY 偏差-0.311-0.611mm;YZ 偏差-0.189-0.229mm;同时对一期和二期两个模型间的最近点变形分量进行了分析。

