一种改进灰狼优化算法

陈建东　聂斌　雷银香

摘  要：针对原始灰狼优化算法（GWO）易陷入局部最优和全局搜索能力较弱的问题，提出一种改进灰狼优化算法（Improved Grey Wolf Optimization， IGWO）。该算法首先通过引入非线性收敛因子来调整控制参数，进一步平衡GWO的全局搜索和局部开发能力。其次，在灰狼位置更新的过程中结合布谷鸟优化算法的搜索机制，帮助灰狼种群陷入停滞时跳出局部最优。最后，在6个基准测试函数进行仿真实验，结果表明IGWO能提升GWO的性能。

关键词：灰狼优化算法；非线性收敛因子；布谷鸟搜索；基准测试函数

中图分类号：TP18  文献标识码：A      文章编号：2096-4706（2023）19-0094-05

An Improved Gray Wolf Optimization

CHEN Jiandong， NIE Bin， LEI Yinxiang

（College of Computer Science， Jiangxi University of Chinese Medicine， Nanchang  330004， China）

Abstract： An Improved Grey Wolf Optimization （IGWO） is proposed to solve the problem that the original Grey Wolf Optimization （GWO） is easy to fall into local optimal and has weak global searching ability. Firstly， this algorithm introduces the nonlinear convergence factor to adjust the control parameter to further balance the global search and local development capabilities of GWO. Secondly， the search mechanism of Cuckoo Optimization algorithm is combined in the process of Grey Wolf position updating to help the Grey Wolf population to jump out of the local optimal. Finally， the simulation experiments on 6 benchmark test functions show that IGWO can improve the performance of GWO.

Keywords： Gray Wolf Optimization; nonlinear convergence factor; Cuckoo Search; benchmark test function

0  引  言

群智能优化算法是基于自然界动物群体行为的模拟而提出的一类优化算法。主要应用于函数优化和全局寻优问题。它具有自适应学习、全局搜索能力和解决高维问题的能力。因此，群智能算法在以下5大领域得到广泛应用[1]：

1）工程优化：群智能算法用于寻找工程问题的最优解，如结构优化、网络优化、资源分配等。2）数学建模：群智能算法用于解决复杂的数学模型，如非线性方程组、动态系统建模等。3）机器学习：群智能算法可用于训练神经网络、支持向量机等机器学习模型。4）图像处理：群智能算法可用于图像分类、图像识别、图像去噪等任务。5）计算机视觉：群智能算法可用于目标跟踪、目标识别等计算机视觉任务。群智能算法在许多其他领域也得到了应用，如特征选择、预测分析等。总的来说，群智能算法是一种非常强大的优化算法，可以解决多种复杂问题。

灰狼优化算法（GWO）是由Mirjalili等人[2]在2014年提出的一种群智能优化算法，它模拟了灰狼对其他动物的捕猎行为，来寻找全局最优解。灰狼优化算法具有较强的随机性和多样性、简单易实现和高效稳定的特点。因此，作为一种有潜力的优化算法，GWO已被广泛应用于各种领域问题。如Fouad等人[3]提出基于GWO的sink节点定位方法，所提出的方法使平均能耗和活动节点数量最小化，并缩短了构建简化拓扑所需的时间。Mosavi等人[4]利用GWO来优化多层感知器神经网络的参数对Sonar数据集进行分类，实验表明该算法在大多数情况下性能优于或与其他算法相当。刘勇等人[5]针对風电波动降低电网对其消纳水平的问题，设计了一种采用GWO改进的自适应噪声的完备集成经验模态分解的混合储能系统功率分配策略，将该策略同其他风电平抑策略进行对比，验证了有效性和优越性。冯麟皓等人[6]针对车间的调度问题，提出了混合交叉搜索策略的灰狼算法，通过MK数据集测试比，验证了算法在多目标车间调度问题的优越性。

然而，同其他群体智能算法相比，GWO依然存在易陷入局部最优，收敛速度较慢等问题。针对这些问题，研究人员进行了大量的改进。Wang等人[7]提出了一种具有进化和淘汰机制的改进灰狼算法（IGWO），实验表明改进后的算法不仅能提高GWO的优化精度而且使算法具有跳出局部最优的能力。Luo[8]提出了一个更现实的模型来模拟自然界中灰狼的领导等级和群体狩猎机制。实验结果表明，改进后的算法在收敛速度和解的质量方面明显优于原有算法。Teng等人[9]提出了一种结合粒子群优化的灰狼优化算法（PSO_GWO），仿真结果表明，该算法能较好地搜索全局最优解，具有较好的鲁棒性。Nadimi[10]等人基于维度学习的狩猎（DLH）搜索策略，提出了一种改进的灰狼优化算法，实验结果和统计测试表明，该算法具有很强的竞争力。Elsisi[11]通过引入基于对立的学习（OBL）和准OB （QOBL），改进了GWO的探索和利用方式，增强了原始GWO的搜索性能，防止算法陷入局部最优。

虽然上述研究人员都对GWO进行了改进，但GWO仍然存在全局搜索与局部搜索不平衡、全局搜索能力较弱的问题。因此，本文通入引入相应的策略对原始GWO进行改进，该算法首先通过引入非线性收敛因子来调整控制参数a，进一步平衡GWO的全局搜索和局部开发能力。其次，在灰狼位置更新的过程中结合布谷鸟优化算法的搜索机制，帮助灰狼种群陷入停滞时跳出局部最优，增强算法的全局寻优能力。在8个基准测试函数的仿真实验表明，改进后算法能提升GWO的性能，表明了改进的有效性。

1  灰狼优化算法

受到狼的狩猎行为的启发，Mirjalili等人[2]提出了灰狼优化算法（Grey Wolf Optimization， GWO）。GWO模拟了灰狼的社会等级和狩猎行为，并将灰狼视为食物链顶端的顶级掠食者。在GWO算法中，狼群中的每只灰狼都代表着种群中的一个潜在解决方案，而领头的α狼则是最佳解决方案。排名第二的β狼和负责侦察、警戒、包围和守卫的δ狼分别代表最佳和次优解决方案。其他候选解决方案是排名较低的ω狼的位置。GWO算法由以下三个步骤组成：

1）初始化灰狼种群位置：在灰狼算法中采用随机产生种群的方法，即：

（1）

式（1）中，X为灰狼位置，i ∈ {1，2，3，…，N}和j ∈ {1，2，3，…，pop}，N为灰狼个数，pop为种群维数；ub，lb分别是搜索上界和下界。

2）种群搜索。灰狼通过式（2）和式（3）追踪猎物：

（2）

（3）

其中，D表示灰狼与猎物的距离；t为迭代次数；A，C为系数向量，分别用于调节灰狼移动的方向和修正猎物位置；X和Xp为灰狼位置和猎物位置。A，C的计算如下：

（4）

（5）

其中，r1，r2为（0，1）之间的随机值，a为控制参数，由下式计算：

（6）

其中，T是最大迭代次數，a在[0，2]范围内取值，随着迭代次数增加线性递减。

（3）种群位置更新。通过计算灰狼优化算法的目标函数值，得到最优解、优解和次优解设为α狼、β狼和δ狼，其他灰狼ω的位置向α狼、β狼、δ狼移

动，完成对猎物的包围，由α狼、β狼和δ狼的位置共同决定，移动公式如式（7）～式（9）所示。重复上述过程，直到满足算法终止条件，最后输出最优解。

（7）

（8）

（9）

其中，C1，C2，C3分别用式（5）计算，A1，A2，A3分别用式（4）计算，Xα，Xβ，Xδ是根据α，β，δ狼的位置生成的新位置，式（9）为ω狼个体新位置更新公式。

2  灰狼优化算法的改进

2.1  引入非线性收敛因子

由GWO的公式可知，其全局探索能力和局部开发能力由参数A决定。当A＜1时，狼群跟随α狼去猎杀猎物；当A＞1时，狼群散开去寻找猎物。然而这种变化是线性递减的，这种线性变化控制了全局搜索的前半段迭代和局部优化的后半段迭代，阻碍了全局探索与局部开发之间的平衡。为进一步平衡GWO的全局搜索和局部开发能力，引入了一个非线性的收敛因子来控制搜索过程，其表现形式如下：

（10）

其中，ainitial代表a的初值，取值为1，afinal代表a的终值，取值为0。t和T分别为当前迭代次数和最大迭代次数。随着迭代次数的增加，在早期，下降速度较慢，使得收敛因子a在较长时间内保持较高的值，从而提高了搜索效率。随着迭代的进行，下降的速度越来越快，导致a在更长的时间内保持较低的值，从而提高了搜索精度，使得算法前期和后期的搜索能力得到较好的平衡。

2.2  结合布谷鸟优化算法更新灰狼位置

由于原始灰狼优化算法中的α狼并不总是朝向全局最优解移动，因此容易陷入局部最优。灰狼群体总是向全局最优的前三个解靠近，其全局搜索能力相对较弱，在求解复杂的优化问题时表现就非常不理想，比如在具有多峰的基准测试函数或一些固定维数复杂函数上的求解。这是因为原算法中的搜索策略单一，导致算法难以找到全局最优解。因此，对灰狼优化算法的搜索策略进行改进，以提高其全局搜索能力和降低陷入局部最优的风险，是十分必要的。而布谷鸟算法的优势在于它能够有效地避免局部最优解，以及具有较快的收敛速度和较高的全局搜索能力。因此通过使用布谷鸟算法的搜索机制来改进灰狼种群的搜索方式能有效解决灰狼优化算法中容易陷入局部最优的问题。

布谷鸟优化算法 （Cuckoo Search Algorithm， CSA）是一种基于布谷鸟觅食行为的优化算法。它是由Yang[11]在2009年提出的。布谷鸟算法的工作原理是模拟布谷鸟的觅食行为。布谷鸟会在觅食地随机地扔下蛋，如果蛋在觅食地里找到了食物，那么布谷鸟会留下该蛋；如果没有找到食物，布谷鸟会随机地选择一个地方再扔下一个蛋，直到找到食物为止。

在布谷鸟算法中，觅食地就是搜索空间，蛋就是搜索点，食物就是目标函数的最优解。每次布谷鸟算法执行一次搜索操作，就相当于布谷鸟扔下一个蛋，并评估该蛋是否是当前最优解。

通过结合布谷鸟的搜索机制，新的灰狼种群的搜索公式如下：

（11）

其中，Xbest为迭代过程中最好的灰狼位置，α为步长控制因子，Levy（λ）为服从莱维分布的随机步长，使用Mantegna算法进行模拟。由式（12）计算：

（12）

式（12）中，，，?μ由式（13）决定：

（13）

式（13）中，β通常取值为1.5。

最后，通过这样的更新过程，耦合灰狼优化算法可以更快地寻找到全局最优解，并且比单独使用灰狼优化算法和布谷鸟优算法具有更高的优化效率和更好的全局搜索能力。此外，由于耦合灰狼优化算法的参数更新方式不仅依赖于当前种群中的个体，还考虑了前一代种群的信息，因此它具有更高的稳定性。

2.3  算法流程

结合上述改进，IGWO的算法步骤如下：

1）算法相关参数初始化，设定种群规模N，最大迭代次数T，搜索范围上界ub，下界lb。

2）根据原始GWO算法中随机初始化种群。

3）计算个体适应度值，记录排名前三的灰狼位置Xα，Xβ，Xδ，然后结合式（3）（9）和（10）得出平均适应度值。

4）如果当前灰狼适应度值小于平均适应度值则按照原有公式进行位置更新；否则，保存当前位置根据式（11）进行位置更新。最后进行适应度比较，保留适应度更高的灰狼个体位置。

5）判断当前迭代次数是否达到设置的值，若达到则输出最优灰狼个体适应度值和位置，否则返回3）。

3  实验与讨论

3.1  实验设计与分析

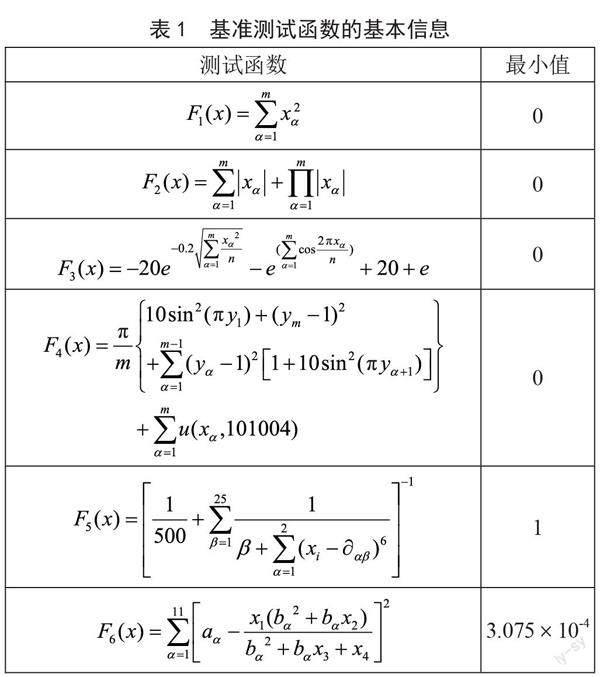
为了验证IGWO的有效性，实验选取已发表文献中的8个基准测试函数测试IGWO的性能，并与原始灰狼优化算法GWO、融合粒子群的灰狼优化算法算法[9]（PSOGWO）进行对比。基准测试函数信息如表1所示，其中F1～F6在30维中运行，F7～F8运行固定维度，每个算法均独立运行50次，实验结果如表2所示。

实验采用最优值（Best）、平均值（Mean）和标准差（Std）来评估IGWO的性能，同时为了展示三种算法的收敛性能，绘制了三种算法在30维的收敛曲线图，如图1所示，其中纵坐标代表适应度值以10为底的对数。

3.2  实验结果与分析

由表2可知：

1）在单峰测试函数F1～F2上，IGWO在最优值、平均值和标准差上相比其他算法均有着更好的表现。其中相比原始GWO和改进算法有着大幅度的领先，说明改进提升了寻优精度和稳定性。

2）在多峰测试函数F3～F4上，IGWO在最优值、平均值和标准差上有着最优值，领先GWO10个数量级。说明改进后在复杂的多峰测试函数上提升了其稳定性和全局寻优能力。

3）在固定维度测试函数F5～F6上，PSOGWO和 IGWO在F5上都取得了近似最优值，IGWO在平均值和标准差上取得了最好的结果。IGWO在F6上在平均值和标准差上依然是最优。

在所有图像中可以发现，随着迭代次数的增加，IGWO相比其他算法收敛速度更快，并且在相同迭代次数的情况下有着更高的精度。其中在F3中，其他算法都陷入了局部最优，只有IGWO收敛于全局最优，表明IGWO有着更强的跳出局部最优的能力。

因此，综合上述分析，在6个基测试函数上的寻优对比实验表明IGWO总体寻优精度更高、稳定性更好和具备跳出局部最优的能力，相比GWO在三个指标数据上有着大幅度的提升。表明改进能进一步提升GWO的性能，改进是有效的。

4  结  论

本文通过对GWO的分析，针对其不足之处提出一种改进灰狼优化算法（IGWO），首先通过引入非线性收敛因子，有效解决了算法全局搜索和局部开发能力不平衡的问题；其次通过耦合布谷鸟优化算法的搜索机制，使得算法具备跳出局部最优的能力的同时提升其全局寻优能力。最后，在8个基准测试函数上的实验验证了IGWO的性能。

参考文献：

[1] CHAKRABORTY A，KAR A K. Swarm intelligence：A review of algorithms [J].Nature-inspired computing and optimization：Theory and applications，2017：475-494.

[2] MIRJALILI S，MIRJALILI S M，LEWIS A. Grey wolf optimizer [J].Advances in engineering software，2014，69：46-61.

[3] FOUAD M M，HAFEZ A I，HASSANIEN A E，et al. Grey wolves optimizer-based localization approach in WSNs [C]//2015 11th International Computer Engineering Conference （ICENCO）. IEEE，2015：256-260.

[4] MOSAVI M R，KHISHE M，GHAMGOSAR A. Classification of sonar data set using neural network trained by gray wolf optimization [J].Neural Network World，2016，26（4）：393.

[5] 劉勇，刘大鹏，穆勇，等.基于GWO优化ICEEMDAN分解的混合储能系统功率分配策略 [J].电气工程学报，2022，17（4）：257-267.

[6] 冯麟皓，方喜峰，李俊.基于灰狼算法的多目标车间调度优化 [J].组合机床与自动化加工技术，2023（1）：168-172.

[7] WANG J S，LI S X. An improved grey wolf optimizer based on differential evolution and elimination mechanism [J].Scientific reports，2019，9（1）：1-21.

[8] LUO K. Enhanced grey wolf optimizer with a model for dynamically estimating the location of the prey [J].Applied Soft Computing，2019，77：225-235.

[9] TENG Z，LV J，GUO L. An improved hybrid grey wolf optimization algorithm [J].Soft computing，2019，23：6617-6631.

[10] ELSISI M. Improved grey wolf optimizer based on opposition and quasi learning approaches for optimization：case study autonomous vehicle including vision system [J].Artificial intelligence review，2022，55（7）：5597-5620.

[11] YANG X S，DEB S. Cuckoo search via Lévy flights [C]//2009 World congress on nature & biologically inspired computing （NaBIC）.Coimbatore：IEEE，2009：210-214.

作者简介：陈建东（1997－），男，汉族，江西赣州人，硕士研究生，研究方向：数据挖掘；通讯作者：聂斌（1972－），男，汉族，江西吉安人，教授，硕导，博士研究生，研究方向：数据挖掘、中医药信息学、中药学;雷银香（1989—），女，汉族，江西井冈山人，讲师，硕士，研究方向：信息安全。

收稿日期：2023-03-09

基金项目：江西中医药大学星火传承培养计划（2252000111/4004）；江西省教育厅科学技术项目（GJJ2200925）;江西省中医药管理局科技计划项目（2020B0412）