面向城市空中交通的eVTOL 飞行器路径规划算法对比
李 明,陈金良,3*,刘 文,王 琳,赵健竹
(1.西华大学航空航天学院,四川 成都 610039;2."智能空地融合载具及管控"教育部工程研究中心,四川 成都 610039;3.吉利科技航空航天学院,四川 成都 641423)
城市化效应使得城市地面交通拥堵问题日益突出。据百度地图发布的《2022 年度中国城市交通报告》[1]显示,全国大中城市的单次通勤耗时普遍在35~50 min。可见,城市地面交通的拥堵问题日益严峻。展望城市上空,电动垂直起降飞行器(eVTOL 飞行器)凭借100 km/h 以上的速度能将城市通勤时间缩短至20 min 内,可有效避免城市的交通拥堵、尾气污染和噪声污染等问题。高效的路径规划方案则是实现这目的的关键,通过智能算法能为单架或多架飞行器生成集群化下的单机最优飞行路径。为此,本文主要从空域规划和路径规划算法两方面展开研究。
1 城市空中交通基本概况
1.1 基本概念
城市空中交通起源于20 世纪60 年代,少数公司用直升机在美国西海岸地区提供点对点的空中通勤服务,但由于安全性、公众承受力和运营成本等问题,这些服务被迫减少以至终止。2017 年,美国国家航空航天局(National Aeronautics and Space Administration,NASA)提出了城市空中交通(urban air mobility,UAM)的概念,即指“在城市中用于客运或货运的、安全高效的有人驾驶/无人驾驶(空中)交通工具系统”[2]。目前,UAM 行业是以电动垂直起降飞行器(eVTOL 飞行器)为最理想化载具。eVTOL 飞行器目前正逐步进入了验证试飞和适航取证阶段,其集成了分布式电力推进、垂直起降和自动驾驶等技术,能在城市低空空域提供安静、快捷的载人和物流服务。
1.2 UAM 的发展前景
由于地面交通的局限性,相关行业与政府机构对城市空中交通的发展前景做了具体调研和分析。在公众层面,2021 年5 月,欧洲航空安全局(EASA)在欧盟进行的关于城市空中交通的一项调查结果[3]显示:83%的受访者对UAM 持积极态度,71%的受访者准备试用UAM 服务;在紧急情况或医疗运输等领域,UAM 得到了受访者的有力支持。在运行成本层面,表1 的亿航发布的一份交通载具成本对比表[4],可以看到eVTOL 飞行器在购置成本、道路建设和运营等方面相比传统交通载具都有明显的经济优势。在产业前景方面,据摩根士丹利预计,到2025 年,全球将有3 000 架飞行汽车投入使用,随后在2050 年将呈指数式增长至10 万架左右,届时全球空中交通产业将达到1.5 万亿美元的规模[5]。

表1 交通载具成本对比Tab.1 Comparison of transport carrier costs
2 空域规划
2.1 相关空域规划理念
城市低空空域具有高密度、高流量和复杂多变等特点。对于未来综合性的城市低空空域主要有2 种规划方向:一是空域结构化,结构化空域是容纳高密度空域最有效的途径,Andrews 等[6]认为结构化空域可以有效降低空域的复杂性和空域管理难度,并且还能促进态势感知,简化警报边界和通过集中式交通中心进行冲突检测;二是空域自由化,Hoekstra 等[7]认为自由飞行优于空域结构化,其航线呈现分布式特点,能有效降低冲突概率,用户可自由选择合适航线,每架飞行器均有独立的分离保障机制,从而减轻了空域的流量限制和结构限制,以应对更高的交通密度。另外,Sunil 等[8]比较了全混合(自由飞行)、层、区和管4 种不同空域结构对高密度空域容量、安全性和效率的影响,其仿真结果表明,分层式空域规划在兼顾容量、安全性和效率方面是最优的。
结合上述空域规划方法,本文以AirMatrix 的综合路由网络[9]为基础,辅以飞行高度层,形成了分层式网格化的城市低空空域规划方案。在AirMatrix 的概念中,城市空间被离散成块,通过防止区块使用中的冲突,形成了一个可管理的整体空域框架,为动态空域的使用提供解决方案。当然,AirMatrix 空域的应用还可以扩展到有人驾驶和无人驾驶的空中交通,以一种协调的方式管理整个城市空域。
2.2 AirMatrix 空域规划方法
AirMatrix 空域规划方法是将城市空域分割成固定大小的三维区块,通过加入时间函数为每一区块形成唯一的四维坐标函数,通过一个城市空域的集中式服务系统对空域使用情况进行精确记录和管理,如图1 所示。在AirMatrix 空域中,飞行器要实时且精准地将飞行数据传输到服务器,而且为了清楚显示每一区块状态,将每一区块的状态可视化为如图1 所示的绿色(未占用状态)、黄色(已计划占用状态)和红色块(占用状态),服务器及其操作人员通过比较实际区块利用率和计划区块利用率来识别每一区块的正常和异常状态[10],从而保障其监控整个城市空域的运行状态,并为实时的运行规划、避障和应急管理的UAM 导航服务供应商提供态势感知。

图1 基于AirMatrix 概念的四维空域示意图Fig.1 Four-dimensional airspace management based on the AirMatrix concept
在 AirMatrix 空域中,将城市低空空域建模为区块状的三维数组,为
式中:Al,w,h是三维区块的物理三维坐标,l、w、h分别是该小块在AirMatrix 空域中X、Y、Z三轴上的方位坐标;Ni由建模空域的大小和每个块的大小计算。对于小块的占用状态则用四维数组表示为{Occupl,w,h,t,t∈{0,1}},即表示为在t时刻Al,w,h的占用状态:若t为0 则没有占用;若t为1 则表示该小块处于占用状态;与静态障碍物和特殊空域重叠的区块则被永久识别为占用状态。
3 eVTOL 飞行器路径规划算法
当前关于路径规划有多种算法,包括:基于概率论的算法,如快速探索随机树(rapidly exploring random trees,RRT)算法和概率路线图(PRM)算法;基于图的优化算法,如Dijkstra 算法和A-star(A*)算法;基于种群的仿生类算法,例如遗传算法和粒子群算法等。由于城市低空空域的环境复杂多变,同时根据NASA 预测的城市空中交通行业发展阶段模型,未来城市低空空域的密度将日益增加。为了实现eVTOL 飞行器在AirMatrix 空域环境下的路径规划,本文根据前人的研究成果[10-13]和AirMatrix 空域环境,从算法细分角度分别选择RRT 算法、改进A*算法和PSO 算法进行分析,以便为eVTOL 飞行器找到更优的路径规划算法。
3.1 快速搜索随机树(RRT)算法
快速搜索随机树(rapidly-exploring random trees,RRT)算法是一种基于对目标点进行概率性采样的递增式路径规划方法。在搜索过程中,算法不断在可行域空间中随机生成状态点,如果该点位于无碰撞位置,则寻找搜索树中离该节点最近的节点,即为中转点,由中转点出发以一定步长向该随机节点进行搜索,该步长搜索的最远点所在的位置被当作有效节点加入搜索树中。搜索树的生长过程一直持续到目标点与搜索树的距离在一定范围内时终止。随后搜索算法在搜索树中反向回溯寻找一条连接目标点到起点的最短路径。
相较A*算法和PSO 算法,RRT 算法通过对状态空间中的采样点进行碰撞检测,由于无须对空间进行复杂的建模,因此节省了算法的运行时间,并且通过状态空间的随机采样点,把搜索导向空白区域,减少了大量无效搜索区域,并最终寻找到一条从起始点到目标点的规划路径[12]。RRT 算法凭借上述优势能够有效地解决高维空间和复杂约束的路径规划问题。但RRT 算法正因为无须对空间建模,当到达NASA 预测的UAM 成熟阶段,该算法的适用性将变得愈发受限[11]。图2 是RRT 算法伪代码,其主要是在给定起始点、目标点和搜索概率的基础上,由起始点向目标点方向通过搜索概率和一定步长向前探查找到几个中间点,再将中间点与目标点间的距离做对比,筛选出最优节点作为下一个探查节点,以此方式直至探查到目标点,最终从目标点反向回溯至起始点找到最优路径。

图2 RRT 算法伪代码Fig.2 RRT algorithm pseudo-code
3.2 A*算法
3.2.1 A*算法
A*(A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法,它在Dijkstra 算法的基础上引入了启发式搜索[14]。图3 为A*算法伪代码。其核心为:使用优先队列,每次从O penList中选择F(ni)最小的节点将其加入 CloseList中,同时扩展相邻节点,可把 OpenList 看成一个优先队列,key值为f(ni),优先级最高的先出。其公式表示为

图3 A*算法伪代码Fig.3 A* algorithm pseudo-code
式中:f(ni)是从初始节点经由中间节点n到目标节点的最小代价估计;g(ni)是在状态空间中从初始节点到中间节点n的实际最小代价;h(ni)是中间节点n到节点的最小估计代价。当h(n)≡0 时,由g(n)决定中间节点n的优先级,此时算法也就退化为Dijkstra 算法;当h(n)>>g(n)时,由h(n)决定中间节点n的优先级,则算法就退化为最佳优先搜索。h(n)是A*算法的启发式函数,也是算法的核心和改进部分[15]。启发式函数的设计影响A*算法的性能:如果启发式值大于实际代价值,算法搜索速度会更快,但不能保证最优性;如果启发式值小于实际代价,则可以达到最优,但会延长算法的搜索时间;最佳启发式函数应接近但不大于实际成本。与Dijkstra 算法相比,A*算法能有效减少算法的搜索步骤,使A*算法速度更快。与RRT 算法相比,通过空域建模,改进A*算法能够实现高密度空域场景下的飞行器路径规划[10]。
3.2.2 改进的A*算法
传统A*算法适用于二维平面的搜索环境,通过曼哈顿距离来实现节点到目标点之间的成本(距离)估计。但eVTOL 飞行器的路径规划环境则是在三维动态空间中,在最短飞行时间轨迹规划中,最小的代价是飞行时间,但eVTOL 飞行器在垂直速度和水平速度有显著差异,这导致在垂直和水平方向上相同的距离会导致不同的时间成本,曼哈顿距离或欧几里得距离也将变得不再适用[16]。因此,需要基于三维路径规划场景下改进启发式函数。图4 是三维邻域下双向A*算法(改进的A*算法)流程图。具体改进策略如下。

图4 三维邻域下双向A*算法流程图Fig.4 Flow chart of bidirectional A* algorithm in threedimensional neighborhood
1)结合AirMartix 空域理念,将每一个三维区块的几何中心点作为算法规划节点,且运用欧氏(欧几里得)距离作为节点到目标点的成本估计,计算公式为
2)将二维场景的8 个搜索邻域扩展至三维场景的26 个搜索邻域,以保证启发函数有最大的遍历范围,提高搜索效率并形成更平滑的规划路径。
3)设置新的启发函数,改进为加权A*算法[17],新的A*算法计算公式为
式中w(ni)是h(ni)的权重系数,w(ni)≥1,权重系数w(ni)改进为动态加权法,提高三维场景下路径规划效率。
4)采用双向A*算法[18],在保证算法路径规划质量的同时提高算法的搜索速率。
3.3 粒子群算法
粒子群算法是模拟鸟类聚集飞行行为的一种仿生类算法。算法中每个粒子个体可感知一定范围内其他粒子个体的飞行信息,并结合当前自身的飞行状态,做出下一步的飞行决策。该算法共有3 条规则:1)避免与相邻个体碰撞;2)相邻个体速度一致;3)向中心聚集。在三维路径规划中,将飞行器的三维坐标看作一个粒子,将可飞空域作为粒子的可行域,城市建筑和其他障碍物作为约束条件,将三维规划路径的长度、平均曲率等视为适应度函数[19]。因此可以将飞行器的三维路径规划过程看成是众多粒子在解空间寻找最优位置的过程[20]。具体算法流程如下:1)将数据初始化,以随机的方式求出每个粒子的初始位置与速度;2)根据每个粒子的3 个散点,拟合得到三维路径;3)依次计算每一个粒子所得到的三维路径的路径长度,作为粒子的适应度值;4)选取这一代适应度最高(即路径长度最低)的最优粒子;5)更新粒子群,根据上一代的位置、上一代更新的速度,得到这一代的位置,粒子速度和位置的更新表达式为
式中:w是惯性权重,表示对当前速度方向的信任程度;c1、c2是加速度常数,调节学习最大步长;r1、r2是2 个 [0,1]的随机值,以增加搜索随机性。粒子群算法主要通过将飞行器的三维坐标粒子散点化,凭借自身粒子本身的过去最优位置和临近粒子过去最优位置来拟合最优的三维飞行路径,其连续性较强,但不适合于离散化问题的路径规划,容易陷入局部最优性,因此要合理分配惯性权重w的取值。w较小,算法的局部搜索能力较强;w较大,算法的全局搜索能力较强[21]。因此要在算法迭代前期赋予w较大值,以尽可能帮助飞行器探测更多较优飞行区域,但在算法迭代后期要赋予w较小值,以期提升算法在极值点的搜索精度,使算法以较大概率向全局最优规划路径收敛,最终找到全局最优路径[22]。
然而,以粒子群算法为代表的这些基于种群的方法存在一些先天缺陷,例如,算法的收敛速率较慢或难以保证,具有不确定性,极易陷入局部最优解[23],从而导致在此基础上进行改进的算法也较难以摆脱这些缺点,使其在UAM 应用的难度较大且成本较高。
4 算法仿真验证及对比
本文在MATLAB(R2022a)平台下,所用计算机操作系统为Windows11,配置64 位CPU,3.2 GHz运算频率,16 GB 运行内存,对RRT 算法、改进的A*算法和PSO 算法进行仿真分析。
RRT 算法的仿真结果如图5 所示。地图大小为1 000×1 000×100,设置起点坐标为(40,129,5),终点坐标为(951,833,10)。在本次仿真飞行中,共进行3 次路径规划,平均解算时间为1.301 706 s,平均最短规划路径为1 431.011 1。
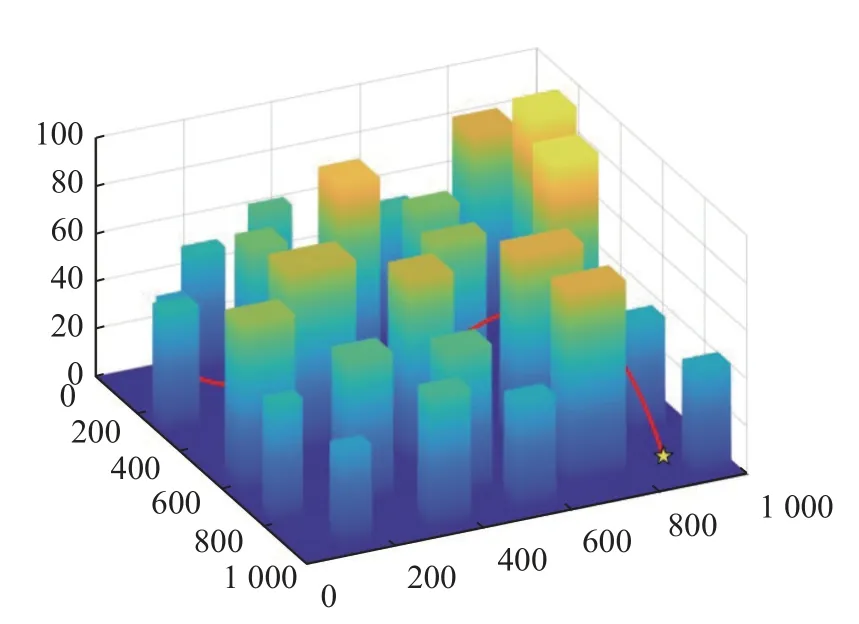
图5 三维地形图中的RRT 算法路径规划Fig.5 RRT algorithm path planning in 3D topographic maps
改进的A*算法的仿真结果如图6 所示。地图大小、起点坐标、终点坐标均与RRT 算法仿真条件一样。在本次仿真飞行中,同样进行3 次路径规划,平均解算时间为7.955 766 67 s,平均最短规划路径为1 151.330 5 。

图6 三维地形图中的改进的A-Star 算法路径规划Fig.6 A-star algorithm path planning in 3D topographic maps
PSO 算法的仿真结果如图7 所示。地图大小、起点坐标、终点坐标均与RRT 算法仿真条件一样,设置了N=10、N=30、N=50 的迭代次数,其中N=50 的迭代次数(历时25.093 678)使算法得到的最短路径长度为1 512.97。

图7 三维地形图中的PSO 算法路径规划Fig.7 PSO algorithm path planning in 3D topographic maps
由以上仿真结果可知,本文基于RRT 算法、改进的A*算法和PSO 算法在同一三维地形图中均能实现较好的路径规划效果。算法具体规划效率如表2 所示 。改进的A*算法的规划路径最短,RRT算法的平均耗时最少。综合可得出,改进的A*算法的路径规划效果最好且耗时适中。
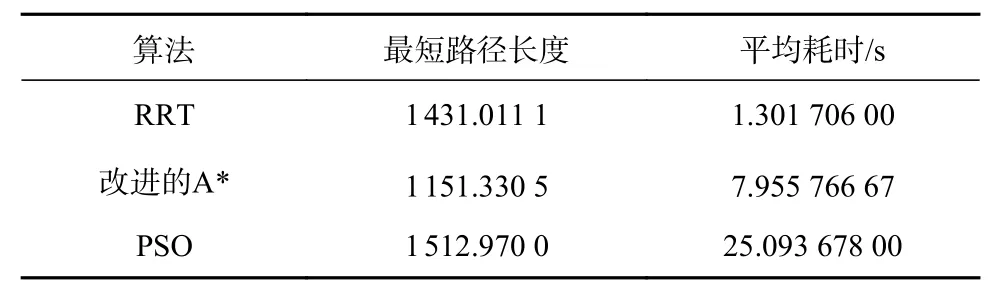
表2 算法综合对比Tab.2 Algorithm synthesis comparison
5 总结
本文以分层式四维AirMatrix 空域规划方案作为未来城市低空空域的规划方法,再结合这一空域规划方案对RRT 算法、改进的A*算法和PSO 算法做了综合对比分析,发现改进的A*算法在低密度城市低空空域环境下为eVTOL 飞行器进行路径规划的综合效率好,RRT 算法和PSO 算法则各有所欠缺。未来,本文将考虑在高密度的AirMatrix空域环境中验证改进的A*算法的路径规划效率。

