面向翼面展开的压电直线位移累积作动器轻量化设计

陆欢欢, 胡凯明, 郑晓亚, 校金友, 宋洪舟

(1.中国计量大学 机电工程学院, 浙江 杭州 310018; 2.西北工业大学 航天学院, 陕西 西安 710072;3.北京精密机电控制设备研究所, 北京 100076)

现有基于电磁伺服电机的舵机定位精度高、功率密度大、响应速度快,是目前小型制导飞行器常用的伺服驱动器[1]。但是对于新一代小型制导飞行器的设计要求,电磁伺服电机主要存在以下三点问题:①电磁伺服电机的寄生电磁场会对飞行器上敏感元件产生干扰,影响制导精度[2];②现有电磁伺服电机需要减速机构,因此会增大伺服系统的质量和体积[3];③随着飞行速度的提高以及制导飞行器体积的减小,其舱内的热量更难耗散,将导致舱内温度快速上升,而电磁式舵机工作温度一般在120 ℃以下[4],温度过高将导致电磁舵机工作精度降低甚至失效。因此亟待开展新型伺服舵机原理和方案的研究。

近年来智能材料结构设计与控制技术的快速发展为解决这一问题提供了潜在途径。智能材料中压电材料能量密度大、机电转化效率高、响应速度快[5],是目前最常用的智能材料之一,但是它的输出位移小(千分之一),难以直接作为大幅值变形的驱动器[6]。为此学者们提出了很多增大输出位移的方法,如柔性铰链法[7]、预压缩法[8]、位移累积法[9]以及将这些方法相互结合的方法等,其中位移累积法是目前大功率大行程压电作动器中最常用的形式。位移累积法压电作动器根据驱动原理的不同,又可分为超声电机、摩擦惯性式压电作动器以及尺蠖式压电作动器。其中超声电机具有结构紧凑、噪声低、断电自锁等优点,但是压电材料磨损较大,发热难以控制[10];摩擦惯性式压电作动器具有结构简单、易于控制、精度高等优点,但是驱动力小[11];尺蠖压电作动器具有驱动力大、输出行程大、输出精度高等优点,因而受到了国内外学者的广泛关注[12]。宾夕法尼亚州立大学的Loverich等[13-14]基于尺蠖作动原理设计了一种新型的大功率直线压电作动器,具有行程大、驱动力大、比功率高、磨损小等特点,非常适用于大驱动力、精度要求高、环境恶劣的场合。

国内在压电直线位移累积作动器方面的研究起步较晚,但是近几年也取得了较好的研究成果。时运来等采用螺旋钳位方式提出了一种新型大推力直线压电作动器,达到了大推力和长行程的效果[15],随后采用双向螺旋箝位的原理,提出一种双向压电直线作动器,该作动器能在受拉和受压负载的情况下驱动[16]。Wang等[17]建立了黏滑压电作动器的动力学模型,利用遗传算法对作动器的柔顺机构尺寸和驱动信号进行优化,提高了驱动速度和驱动力。胡俊峰等[18]采用柔顺机构,提出了一种新型尺蠖型式直线微驱动器,在保证驱动力及箝位力的情况下,提高了运动速度。李建平等[19]利用激光对射传感器感知永磁体位置产生控制信号来驱动压电堆直线位移输出的方法,提出了一种基于旋转磁铁箝位的新型压电尺蠖驱动器,简化了压电尺蠖驱动器信号控制系统,并降低了摩擦磨损。赵勃等[20]提出了一种基于导通角调节的推进式尺蠖电机驱动方法,使电机实现了高速和高位移分辨率。然而,目前对尺蠖压电作动器的轻量化设计研究较少,导致其能量密度不高,距离应用还有较大差距。

针对制导飞行器上翼面展开驱动器设计要求,压电作动器不但要满足展开时间要求,还应使质量与体积最小化。因此本文将从以下两方面进行研究。其一是建立新型的压电直线位移累积大功率作动器的虚拟样机,通过与实验数据对比验证虚拟样机模型的可靠性。其二是将作动器应用于制导飞行器的翼面展开,通过建立作动器参数化虚拟样机模型,利用多岛遗传算法对作动器质量进行优化,从而建立一套压电直线位移累积大功率作动器的轻量化设计方法,以便指导后期结构轻量化设计。

1 虚拟样机建模与分析

1.1 虚拟样机建模

压电直线位移累计大功率作动器通过丝杠螺母以及小型力矩电机的配合来累积由压电堆产生的高频微小位移,如图1所示。其具体过程为:假设上部丝杠承受外部压力载荷,首先对压电堆施加正电压使其伸长,推动上部丝杠与上螺母脱离;然后通过力矩电机驱动上螺母转动, 扭矩使上螺母与上部丝杠相互楔紧;接着对压电堆施加负电压使其缩短,带动下部丝杠与下螺母脱离;最后通过力矩电机带动下螺母转动,使其与下部丝杠楔紧,由此完成一个向上推动的运动周期。

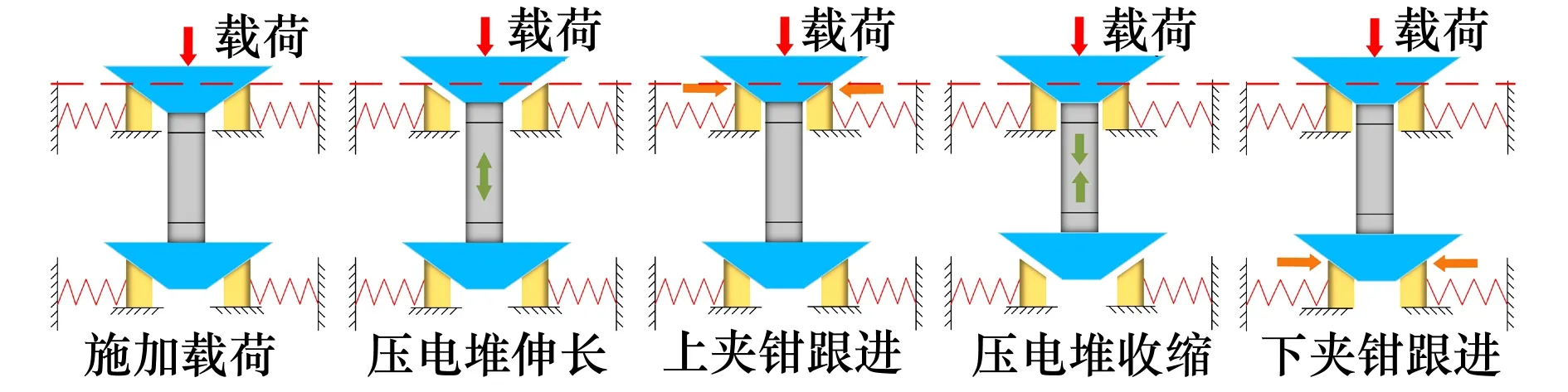
图1 压电直线位移累积原理

作动器的虚拟样机模型,如图2所示,该模型由上盖、上螺母、支撑盖、下螺母、压电堆盖、丝杠、下盖、压电堆、电机转子、电机定子以及外壳等组成。其作动原理为:压电堆推动下螺母上升,下螺母推动丝杠上升;上螺母在力矩电机驱动下楔紧丝杠;下螺母在电机驱动下实现下旋,同时压电堆回缩。对压电堆施加周期电压并使电机协同作动,便能实现丝杠的大位移伸出。由于压电堆受简谐波电压激励,长度会产生周期性变化,因此将压电堆简化为弹簧质量系统,并且连接下盖和压电堆盖,其等效质量施加于压电堆盖上。

图2 压电直线位移累积高功率密度作动器虚拟样机模型

1.1.1 运动副设置

作动器下盖与地面之间设置固定副;作动器外壳与下盖之间设置固定副;支撑盖与外壳之间设置固定副;上盖与支撑盖之间设置固定副;上、下螺母与丝杠间设置圆柱副与螺旋副,从而保证螺母在丝杠上做轴向螺旋运动;丝杠与上盖之间设置有移动副,保证丝杠仅做轴向运动;压电堆盖与压电堆固定,而压电堆在电压驱动下,做轴向伸缩,因此在压电堆盖与地面之间建立沿压电作动器轴向的移动副。

1.1.2 驱动和接触力设置

由于压电作动器在运行时,下螺母的下端面与压电堆盖有直接接触,包括了碰撞和摩擦,因此在下螺母与压电堆盖之间设置接触力。根据已有文献可知[21],当下螺母与压电堆盖材料为结构钢时,可将碰撞力指数设为1.5;结构钢之间的阻尼系数设置为50 N/(mm·s-1);穿透深度设置为0.1 mm。由于其相互作用力较大,将接触刚度设置为3.5×105N/mm;由于是干摩擦,其静摩擦因数设置为0.3,动摩擦因数设置为0.25,静平移速度设置为0.1 mm/s,摩擦平移速度设置为10 mm/s。同时,上螺母下端面与支撑盖之间也经常会有碰撞及摩擦,因此对上螺母与支撑盖之间设置与下螺母和压电堆盖之间相同的接触力。

无框力矩电机的扭矩与速度不遵循线性关系,但在小范围的电机转速内,可以选择一恒定阻尼使模型电机与实际电机的失速扭矩和峰值功率点相匹配。其定子与转子间的扭转阻尼参数为[22]

(1)

式中:Tbias为无框力矩电机的失速扭矩;Tpp为无框力矩电机在峰值功率下的扭矩;ωpp为无框力矩电机在峰值功率下的角速度;r为丝杠节圆半径。

电机转子与螺母通过扭转弹簧连接,在虚拟样机中将扭转弹簧等效为扭转刚度及扭转阻尼,其表达式分别为[23]:

式中:Es为扭簧材料模量;d为扭簧丝截面直径;D为扭簧中径;n为扭簧有效圈数;ξ为扭簧系统的相对阻尼系数;mnr为等效螺母质量,扭转刚度单位为N·mm/(°),扭转阻尼单位为N·mm·s/(°)。

虚拟样机中所选取的压电堆阻塞力FB、压电堆刚度Ks、频率f、电机力矩等参数可根据实际情况而定。压电堆阻塞力及其刚度分别可表示为

(4)

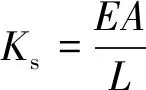
(5)

式中:E为压电堆弹性模量;A为压电堆截面积;L为压电堆长度;ΔL为压电堆最大电压驱动下的输出位移。

1.2 虚拟样机与实验对比

为了验证虚拟样机模型的准确性,将虚拟样机仿真结果与文献[22]实验数据进行对比。虚拟样机模型采用表1中的参数进行仿真。

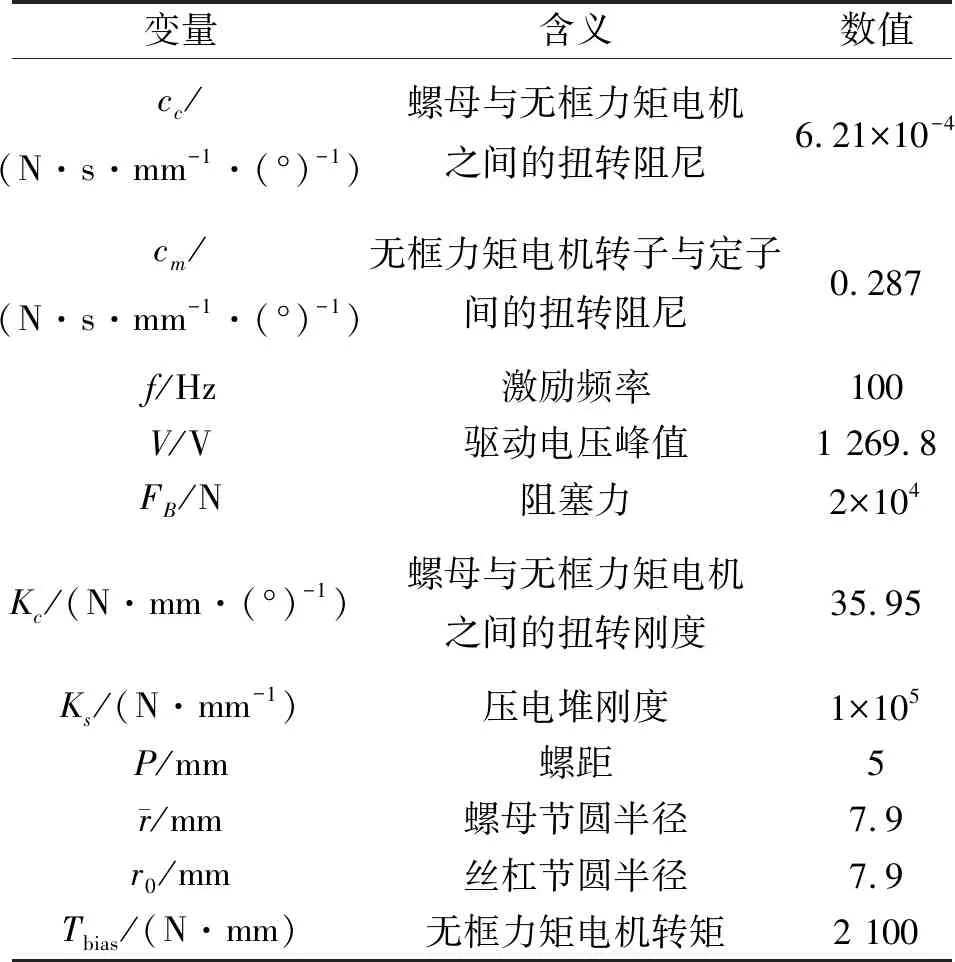
表1 仿真参数表[22]

图3为虚拟样机与实验结果的对比图,图中显示了作动器在不同输出速度下,作动器所受载荷以及虚拟样机相对于实验结果的绝对误差。

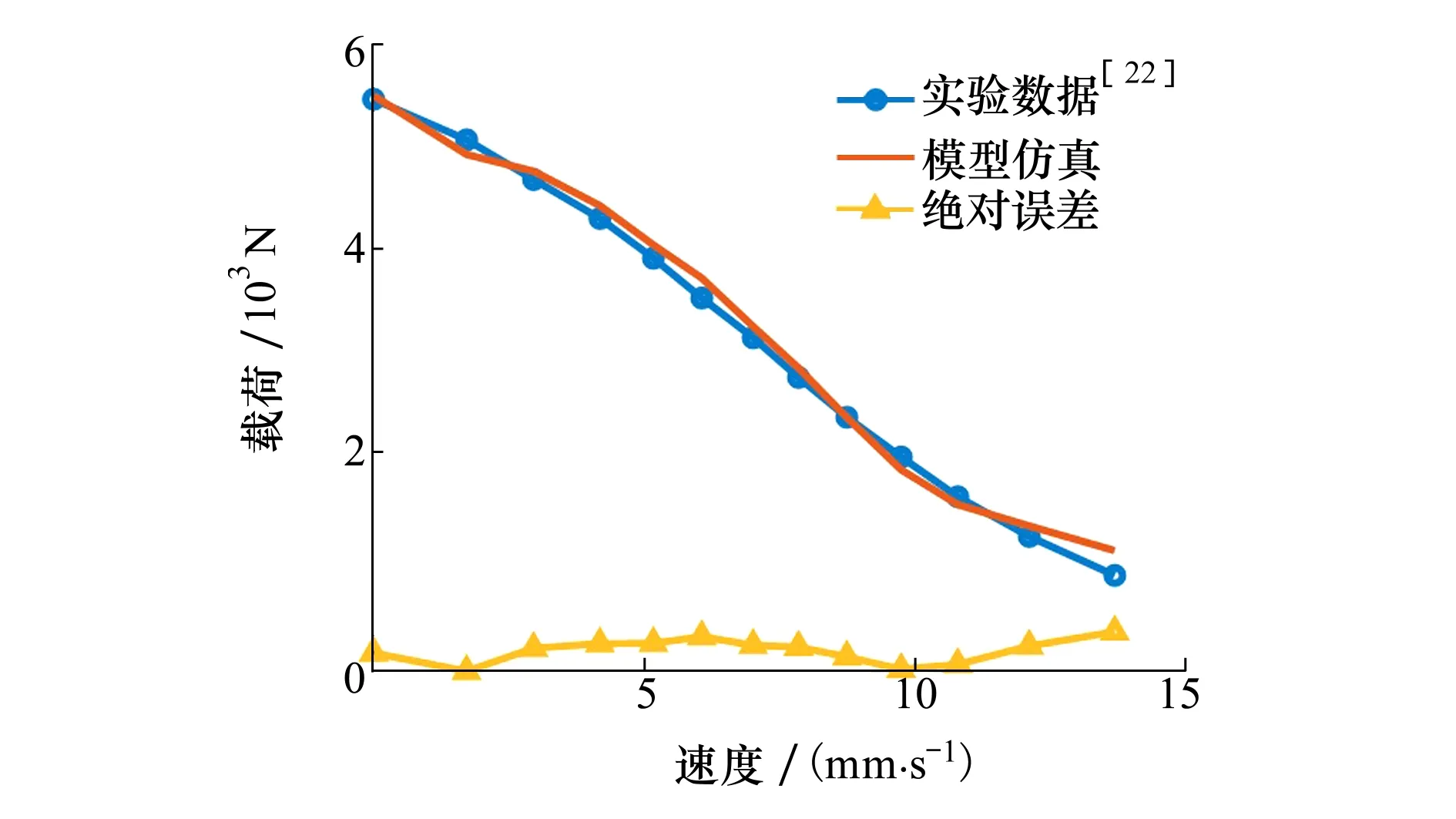
图3 实验与虚拟样机的输出位移对比图

虚拟样机仿真与实验数据的相对误差为

(6)

2 优化目标及优化方法

2.1 优化目标及优化参数

为了能将压电直线位移累积大功率作动器应用于制导飞行器翼面展开机构的驱动,需要获得翼面展开情况下的作动器设计指标要求。翼面展开机构及其展开过程如图4所示,采用齿轮齿条机构,使翼面在0.25 s内从0°转动至90°。

图4 翼面展开机构

由于飞行器具有一定的速度,因此翼面在展开过程中会受到空气载荷的阻碍。当飞行器在1个大气压,攻角为12°,0.7马赫工况下,翼面受到的法向力FY、沿飞行器轴线方向力FZ、垂直于轴向的展向力FX随展开角的变化如表2所示。

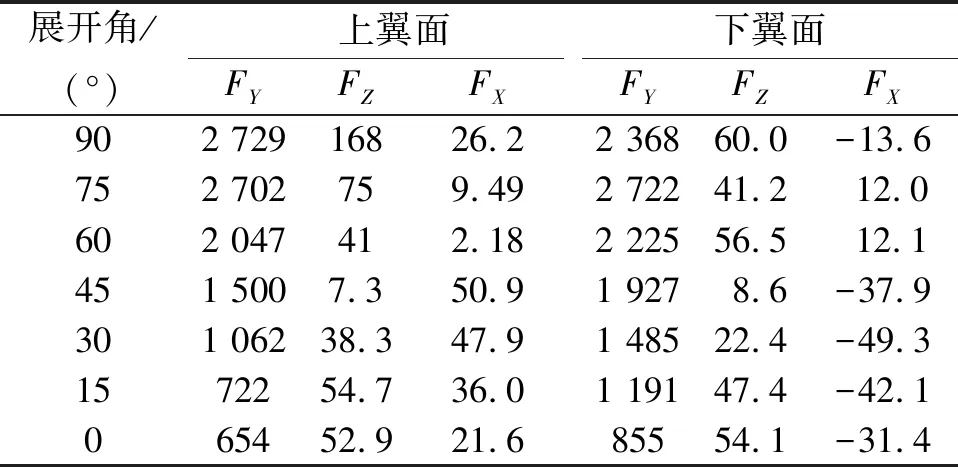
表2 翼面在不同展开位置时作用在压心的气动力 N

事实上,模型中的力还应包括齿轮轴与轴承之间摩擦力、齿轮齿条间的接触力、翼面气动载荷以及作用在齿条上的外力。考虑到气动力占主要成分,为了简化模型,在设计之初假设作动器只受到气动载荷。在翼面展开角为任意角度时,单个翼面的气动载荷对齿轮转轴的力矩为

(7)

式中:R为翼面质心到齿轮转轴中心的距离;θ为翼面转角为0°时,其质心与齿轮转轴中心连线与飞行器轴向之间的锐角;作动器输出位移为s;齿轮分度圆半径为r;转轴中心坐标为(0,0)。

此时单个翼面对作动器的作用力为

(8)

在综合考虑展开时间和空间尺寸的限制后,将齿轮的分度圆半径选取为8.5 mm,在此情况下作动器0.25 s行程需达到13.35 mm才能满足展开要求。本文的作动器轻量化设计问题转化为作动器在0.25 s行程为13.35 mm的条件下来实现质量最小。

为了便于作动器优化设计,避免在优化过程中重复计算不同翼面展开位置下的作动器受载,为此采用翼面随展开角变化曲线代替实际气动载荷对压电堆作动器的作用力。结合翼载计算结果以及(7)～(8)式,即可得到该载荷曲线,如图5所示。

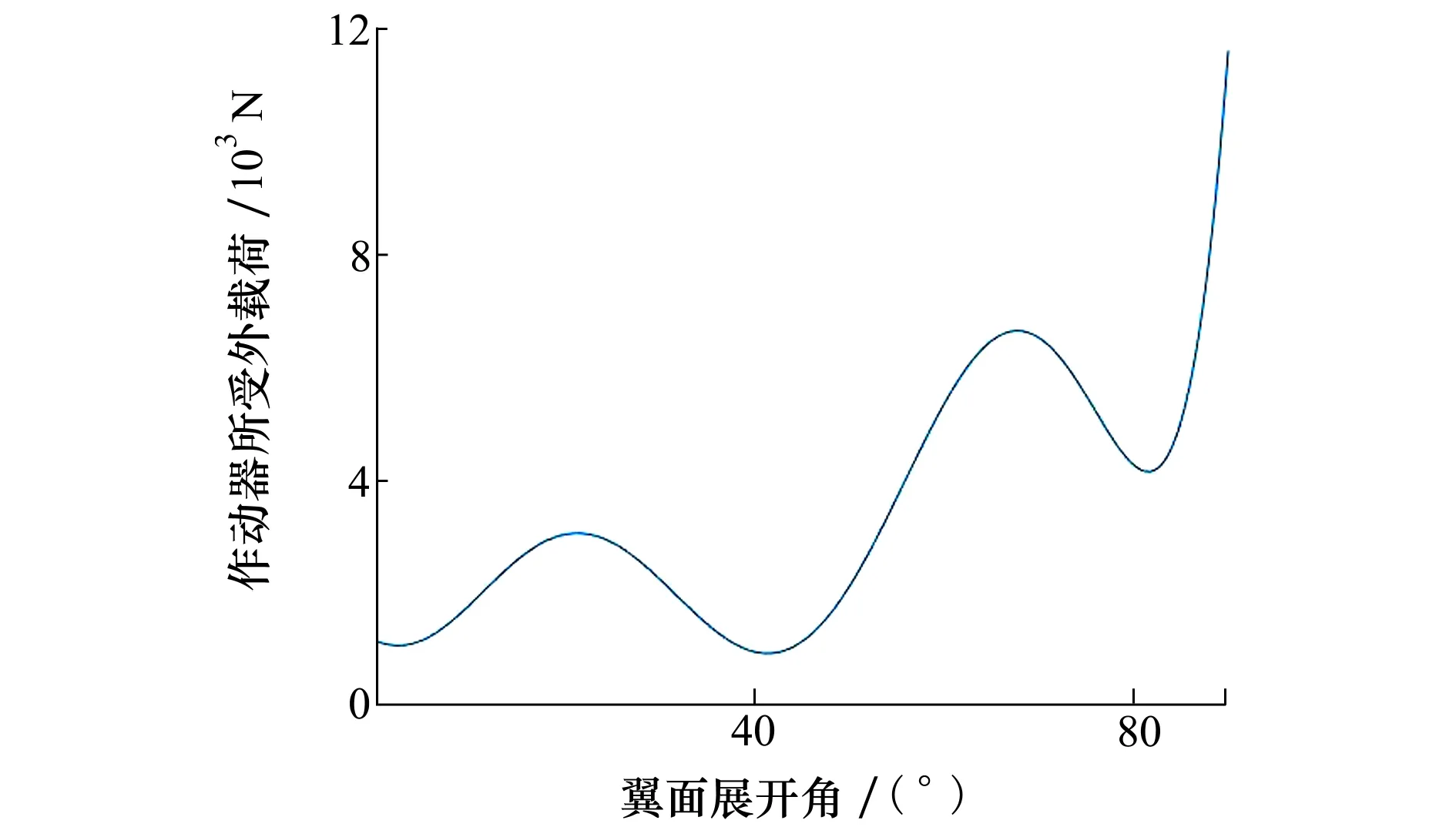
图5 估算气动载荷对压电堆作动器的作用力

为了建立压电作动器轻量化设计模型,需对作动器进行参数化建模。由(4)～(5)式可知,压电堆的长度和截面积对压电堆阻塞力以及压电堆刚度有影响,不但影响压电作动器输出位移,还影响作动器外壳、下盖、支撑盖、上盖以及丝杠等质量。压电堆激振频率会影响作动器在单位时间内的位移。无框力矩电机的力矩不但会影响作动器在每次振动中的输出位移,而且会影响作动器外壳、支撑盖、上盖以及电机的质量。所以压电作动器的输出位移、速度和质量主要与压电堆的激振频率、长度、截面积以及无框力矩电机力矩有关。压电堆截面积可通过压电堆外径计算得到,所以在参数化模型中,将压电堆激振频率、压电堆长度、压电堆外径以及电机力矩作为主要参数,对压电作动器进行参数化建模。电机力矩与电机型号有关,使用的电机型号如表3所示。通过以上4个参数对压电作动器进行建模,对各尺寸进行控制,通过调节4个参数,实现对压电作动器的轻量化设计。

表3 无框力矩电机型号表[24]

2.2 基于Isight的作动器轻量化

优化设计的每组参数都需要进行三维建模以及动力学分析,过程复杂,为了省去反复操作,本文通过Isight集成Adams进行轻量化设计。基本步骤为:

1) 选取合适的设计变量、优化目标及约束条件,建立优化模型。

2) 利用Isight的数据交换器产生后续流程需要的设计变量参数。

3) 利用Isight集成Adams,接收数据交换器的输出参数,实现自动建模,并进行动力学分析,提取作动器的质量以及输出位移。

4) Isight提取步骤3)中的输出参数,完成实验设计以及优化设计。

在作动器轻量化设计中,首先进行实验设计(DOE),分析各设计变量对作动器的影响程度,为参数范围的选取提供依据,在此基础上进行优化。基于Isight集成Adams的实验设计和优化设计基本流程如图6所示。

本文定义作动器相关参数及初始值为:压电堆外径D=40 mm,长度L=500 mm,无框力矩电机力矩T=2 400 N·mm,激振频率f=200 Hz。

根据作动器的结构参数以及实际应用需求,建立优化模型:

(9)

式中:m(D,f,L,T)为优化目标函数,即作动器质量最小;x(D,f,L,T)为作动器在0.25 s内的输出位移。

实验设计能够确定不同影响因子对作动器的输出位移和质量的影响程度。本实验设计采用自适应DOE方法,该方法使用一组设计点对空间进行采样,以使相邻点之间的最小距离最大化,非常适合不连续设计空间和长时间运行的模拟。为平衡实验设计的计算精度以及计算时间,实验设计设置样本点数为300。

优化设计采用多岛遗传算法。多岛遗传算法不依赖于求解问题的连续性,在求解较为复杂的组合优化问题时,相较于传统遗传算法能进一步增加种群的变异性,防止出现早熟现象,其工作流程图如图7所示。优化设计中设置子种群大小为10,岛屿数量为10,遗传代数为10,交叉率为1,变异率为0.01,迁移率为0.01,基因尺寸均设为6。

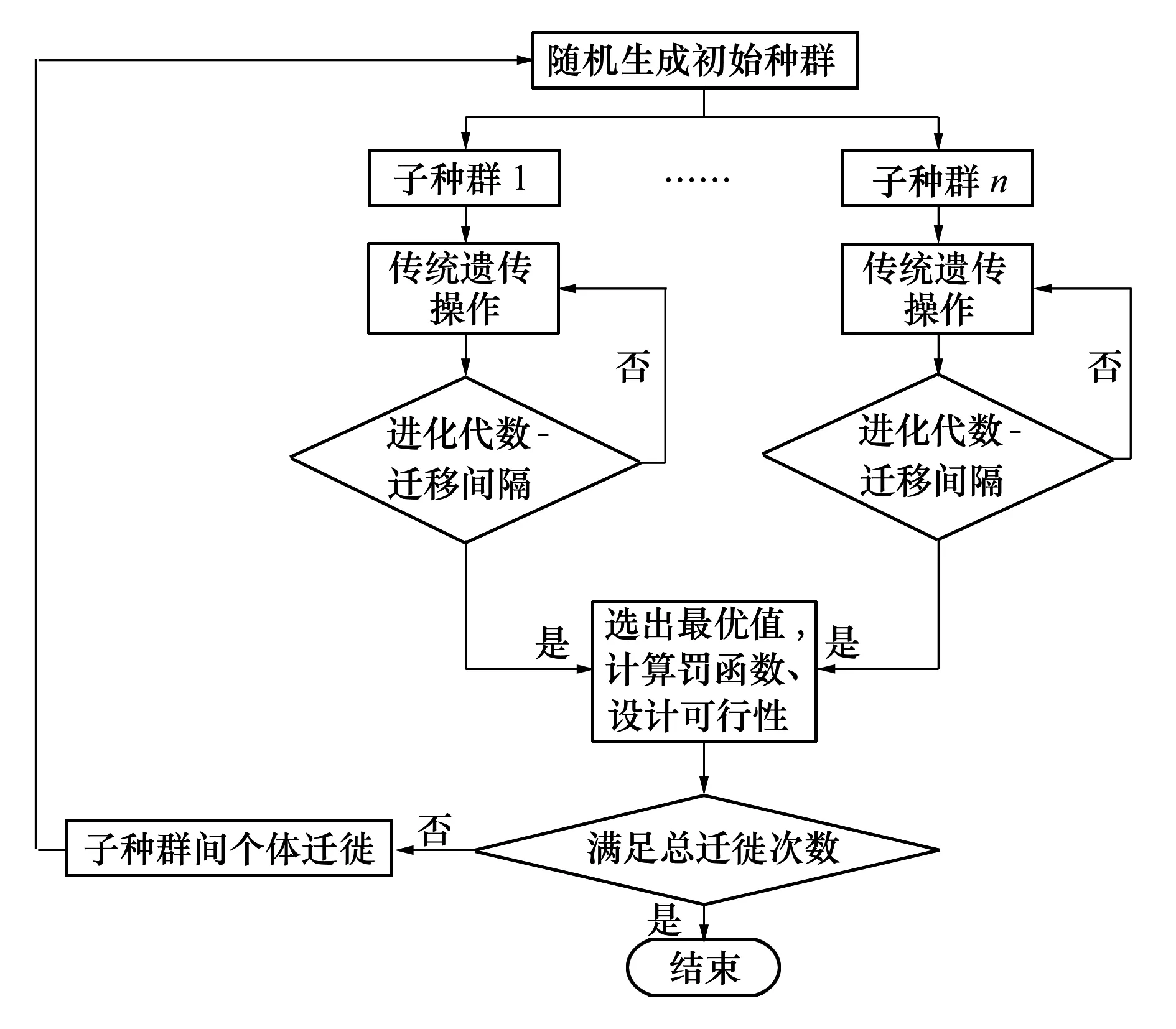
图7 多岛遗传算法的工作流程图

为了提高优化速度和效率并避免优化结果陷入局部最优,对作动器进行2次优化,在第一次优化之后,对优化结果进行分析,缩小参数的取值范围,再进行第二次优化,具体优化过程在第3节中介绍。

3 优化过程与结果分析

3.1 第一次参数分析

实验设计法能够得出各优化参数影响因子对于作动器位移及质量的影响程度,实验设计中参数的范围如(9)式所示。图8为所有参数影响因子对作动器0.25 s输出位移的主效应图。由图可知,压电堆激振频率对作动器输出位移的影响最大,随着激振频率的增加,作动器的输出位移先增大后减小;无框力矩电机的力矩对作动器输出位移的影响次之;压电堆长度对作动器输出位移的影响较小,且呈弱线性关系;压电堆外径对作动器输出位移的影响最小。由图可知,在实验设计中,所有的设计点均未能满足作动器公式(9)中的输出位移约束条件,故作动器在优化过程中,若要满足约束条件,需要选取适中的压电堆激振频率以及较大的无框力矩电机的力矩和压电堆长度。

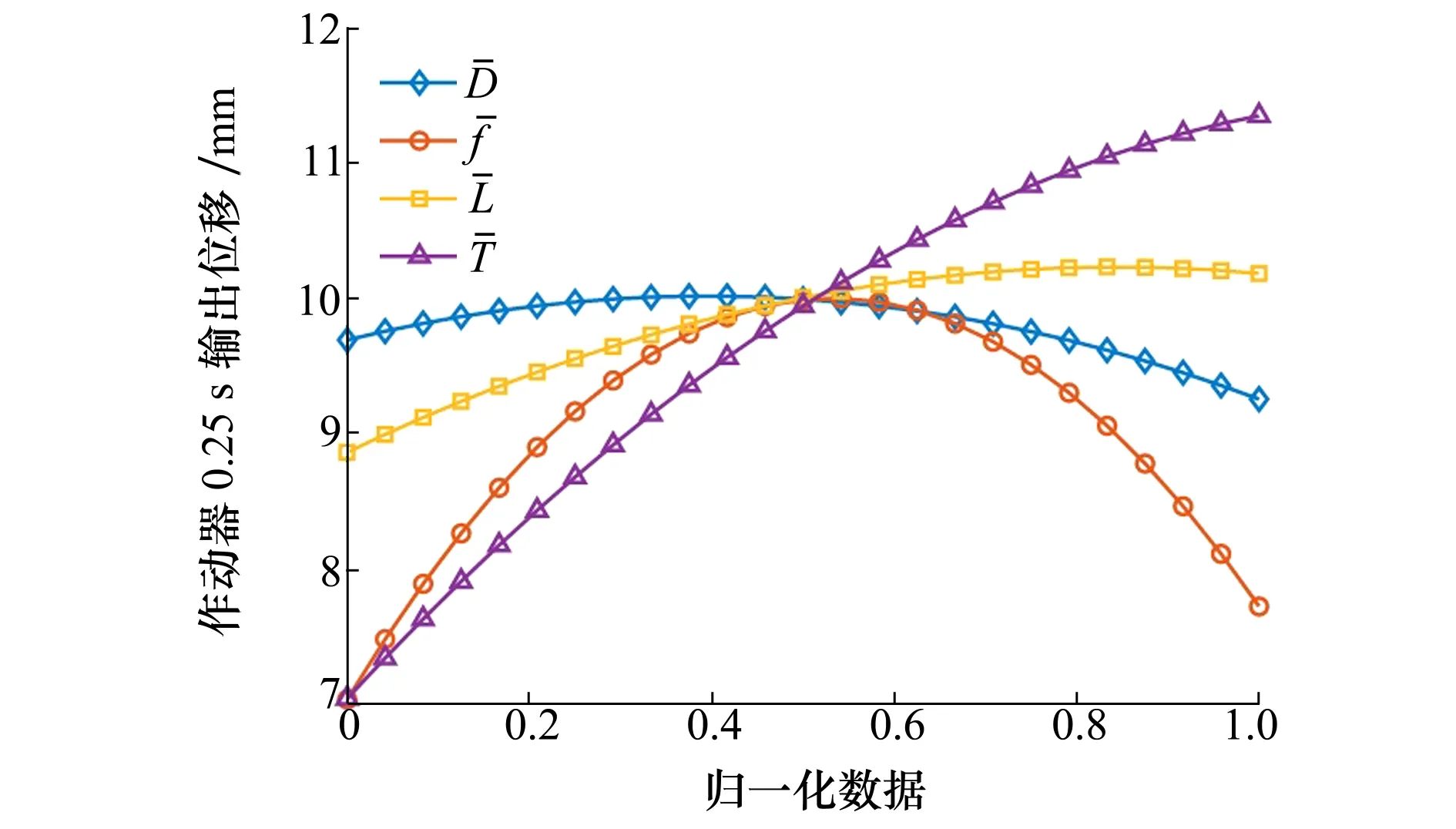
图8 优化参数因子对作动器输出位移的主效应图

图9为所有因子对作动器质量的主效应图。由图可知,压电堆外径对作动器质量影响最大,且基本呈线性关系,压电堆长度堆对作动器质量影响次之,压电堆激振频率对作动器质量影响最小,几乎没有影响。故在作动器轻量化时,需要尽可能降低压电堆的外径,适当减小压电堆长度以及电机力矩。

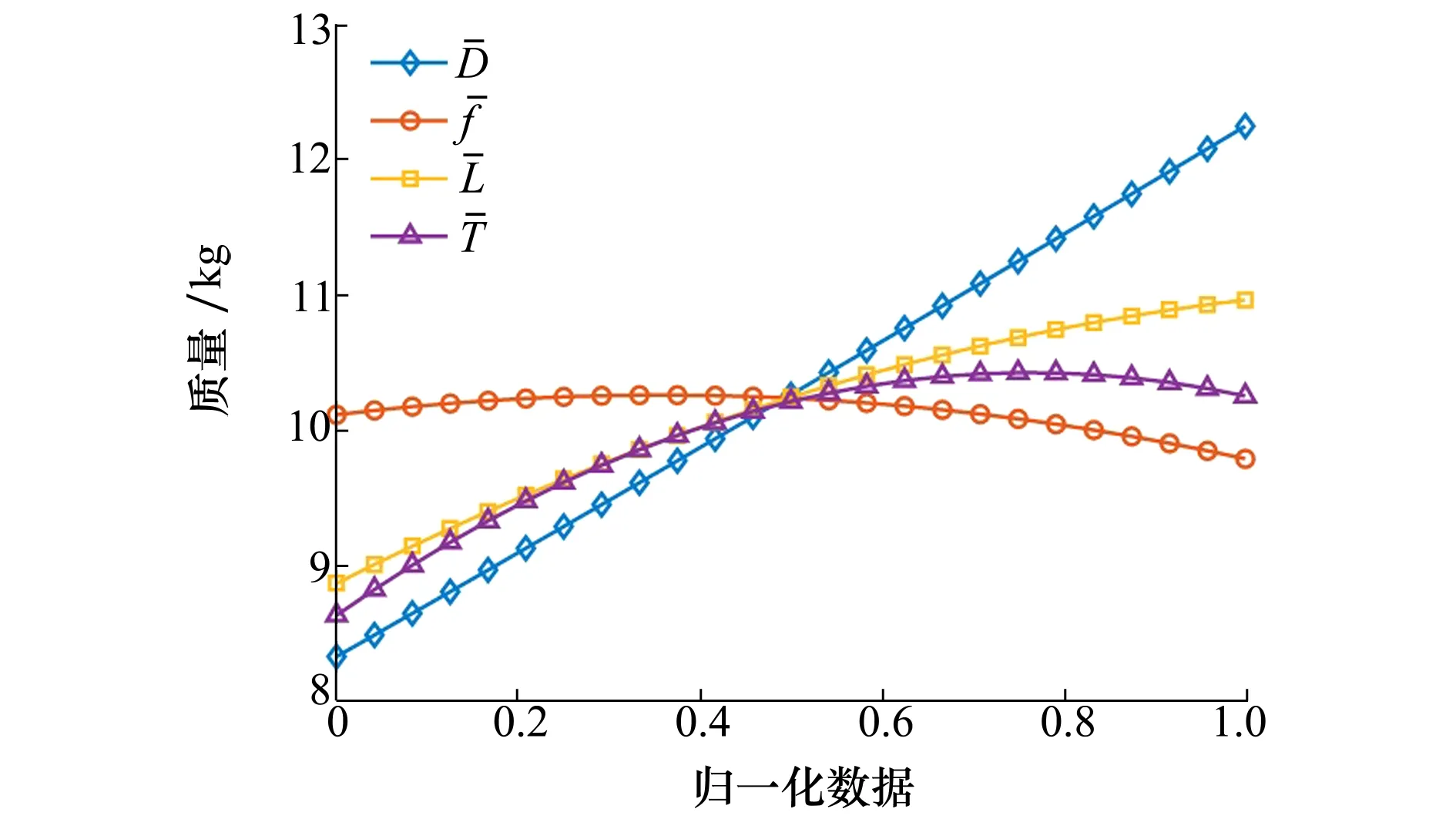
图9 优化参数因子对作动器质量的主效应图

3.2 第一次优化

利用多岛遗传算法进行优化设计可确定设计点的可行性。图10为设计可行性的历史图,图中不可行解为不满足0.25 s作动器输出位移13.35 mm的设计点;劣解为满足约束条件,但不是最优解;推荐设计点是满足设计条件的最优设计点。

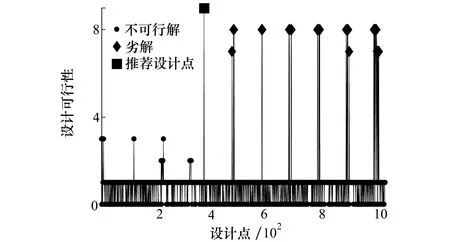
图10 设计可行性的历史图

第一次优化后可以得到压电堆振动频率f为135.71 Hz,压电堆直径D为36.67 mm,压电堆长度L为592.06 mm,无框力矩电机的力矩T为3 803.4 N·mm时,压电作动器能够满足在0.25 s内输出位移达到13.35 mm,并且其质量最小,为10.28 kg。

3.3 第二次参数分析

由于在第一次优化时,作动器参数取值范围较大,通过缩小参数取值范围,进行优化设计,能够进一步减轻作动器质量。而在进行第二次优化前,需要再进行一次DOE实验设计,对第二次优化的参数范围进行选取。在第一次优化之后,注意到,压电作动器需要满足约束条件,则无框力矩电机只有095BL型号才能够满足,压电堆长度则需要大一些,压电堆的激振频率不能太高。故第二次DOE实验设计的参数范围设置如表4所示。

表4 第二次DOE实验参数范围表

图11为第二次DOE实验所有因子对作动器0.25 s输出位移的主效应图。图12为第二次DOE实验设计所有因子对作动器质量的主效应图。由图可知,作动器激振频率对输出位移影响很大,并且随着激振频率的增加,作动器输出位移先增大后减小,而对质量没有影响,故需将激振频率调节到一个适中的范围;压电堆的外径对质量影响很大,对输出位移影响较小,故作动器直径需要尽可能小;电机力矩对作动器的输出位移具有一定影响,对作动器质量没有影响,故无框力矩电机的力矩需要取最大;压电堆长度与作动器输出位移及质量都是正相关,故压电堆长度需要取值适中。

图11 第二次DOE因子对作动器输出位移的主效应图

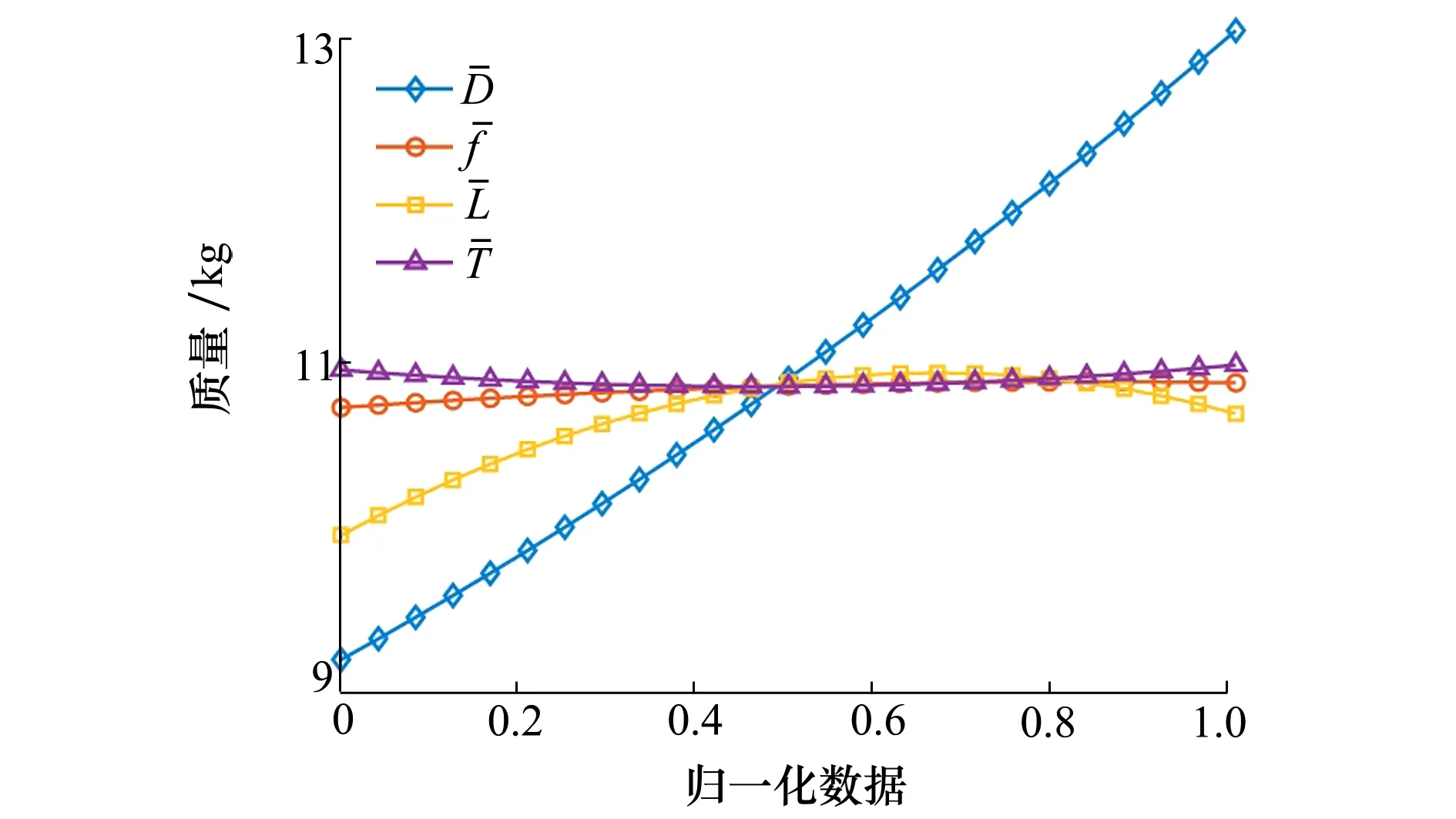
图12 第二次DOE因子对作动器质量的主效应图

3.4 第二次优化

通过第二次DOE实验设计的结果,对作动器进行第二次优化设计,其参数范围如表5所示。

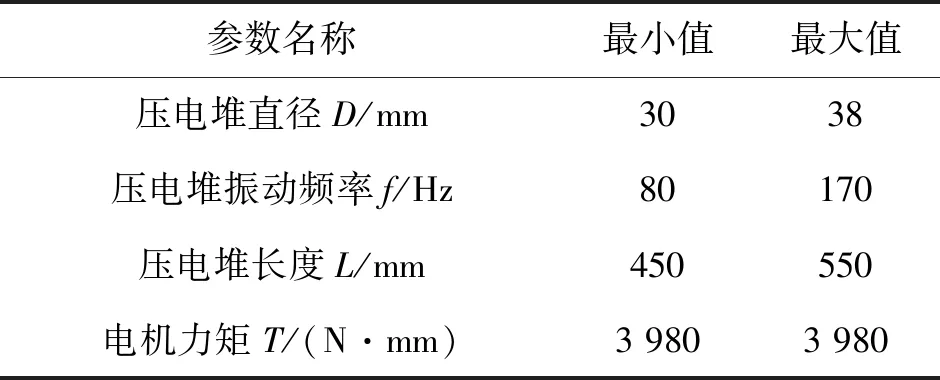
表5 第二次优化设计参数表

作动器质量的优化曲线如图13所示,最终得到压电作动器优化后的质量为8.44 kg。优化后,无框力矩电机转速如图14所示,由图可知,无框力矩电机转速在095BL型电机额定转速的使用范围内。压电作动器的设计参数在表6中列出,其中功率密度通过平均功率与作动器质量之比所得,相较于Loverich的设计方案[22]提高了75%。

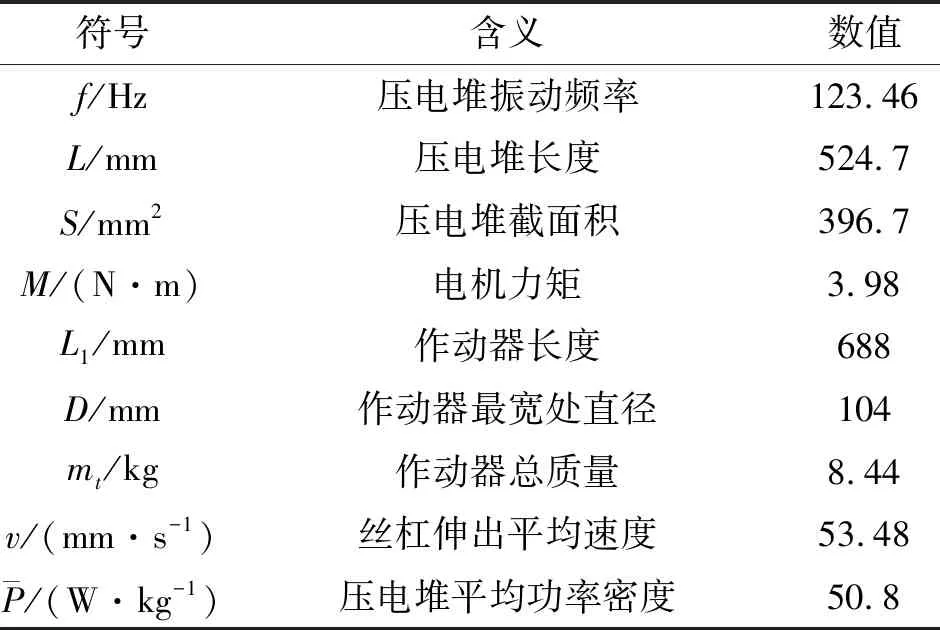
表6 压电作动器优化后方案的设计参数值

图13 作动器质量的优化曲线图

图14 优化后无框力矩电机转速

图15为初始值状态和优化方案下作动器的输出位移。初始值状态下,作动器在0.25 s内输出位移为7.65 mm,未能满足约束条件,优化之后,作动器的输出位移达到13.35 mm,满足约束条件。初始值状态下,作动器的质量为10.46 kg,优化之后作动器的质量为8.44 kg,优化后作动器质量相对于初始状态下作动器质量减小了19.3%。

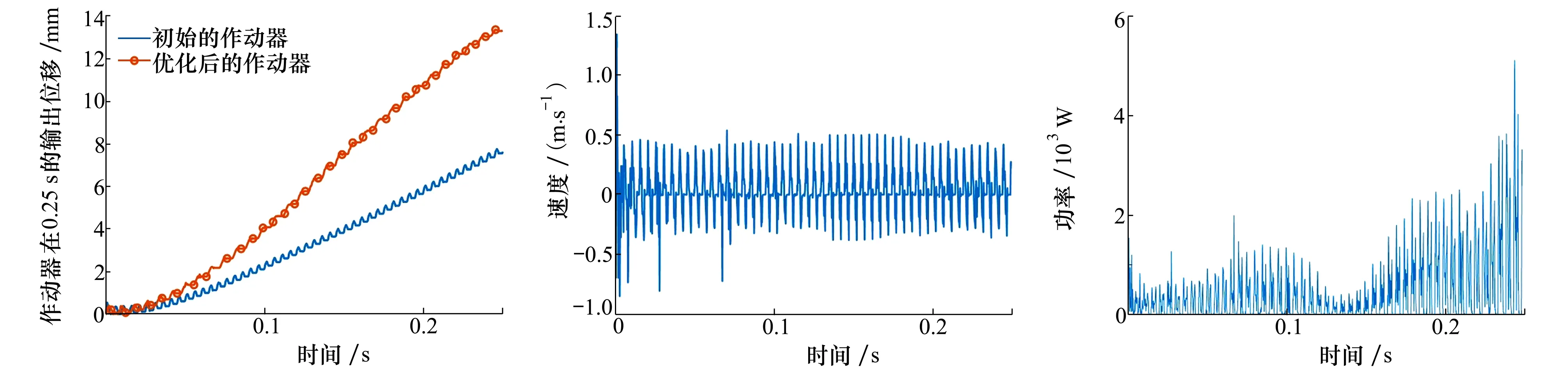
图15 初始方案与优化方案输出位移对比图 图16 最优方案作动器速度变化图 图17 最优方案作动器功率变化图

最优方案作动器的输出速度变化如图16所示,作动器的功率变化如图17所示。由图可知,翼面在展开过程中作动器输出位移呈阶梯递增,并且位移输出速度以及作动器功率随时间变化的波动较大,这主要是与压电堆受到的周期性激励电压有关。

4 结 论

本文针对压电直线位移累积作动器轻量化设计问题开展了虚拟样机参数化建模与优化研究,得到了以下结论:

1) 本文建立了压电直线位移累积作动器的虚拟样机模型,通过虚拟样机仿真结果与实验数据对比,验证了虚拟样机模型的有效性。

2) 本文对虚拟样机参数化模型(压电堆直径、长度、激振频率、电机力矩等参数)进行了DOE分析及基于多岛遗传算法的参数优化,实现了对一定展开要求下的作动器结构轻量化设计,作动器达到了50.8 W/kg的功率密度,接近于电磁伺服舵机功率密度。

下一步将根据本文优化方案制作原理样机,并开展实验验证,为不同需求下压电直线位移累积大功率作动器的轻量化设计提供参考。